機械学習について
niku今まで、適当にコードを書いて機械学習を実行してみたが、nanが出力されてしまう状況だった。
pytorchを使っていたのだが、そもそも、上っ面のコードを真似て少し変更という形式で実装していたので、何が悪かったのか検討もつかない状況だ。
なので、pytorchでできることは何だろうか、どこを読めばいいのだろうかと探した結果、今の自分に最適な情報源かどうかはわからないが、https://pytorch.org/tutorials/beginner/basics/intro.html
から順々に読み進めていた。
Zennに出会ったのはつい最近で、すでにhttps://pytorch.org/tutorials/beginner/basics/autogradqs_tutorial.html
の手前までは読んでいるので、ここから読み進めて記録する
niku
§Automatic Differentiation with torch.autogradを読む
読んだ結果覚えるべきことをまとめると
・ニューラルネットワーク学習用アルゴリズムのデファクトスタンダードはback propagation
・例に漏れずpytorchでもback propagationを導入している
・back , propagationとは学習可能な変数wを持つ
を用いて L(w)を最小化するパラメータwを探す方法
・PyTorchでは勾配計算のために torch.autogradと呼ばれる微分エンジン（何それ？）が組み込まれている。
・torch.autogradは任意の計算グラフ（何それ？）の勾配の自動計算をサポートする。
（感想：書いてあることは理解できていないが、単純に勾配を簡単に計算できるモジュールがtorch.autogradなのだろう）
nikuTensors, Functions and Computational graphを読む
表示されている計算グラフについての感想：
グラフを観察すると、
データ（入力データ、教師データ、パラメータ）と損失関数がリーフ
演算がノード
になっていると思ったが、データzはノードなので、そういうわけでもなさそうだ。
データと演算がごっちゃになってるが、こんな図でよいのだろうか？
ということで計算グラフ作成時のマイルールを作ってみる。
計算グラフの自分ルール：
- データ（Tensor）は長方形で表現
- 演算・関数（Function）は丸で表現
- データ（Tensor）の流れを矢印で表現
- データでもパラメータは灰色に色付けする
ということにする。
覚えるべきこと：
・PyTorchではデータはtorch.Tensorオブジェクトである
・パラメータ（学習可能なデータ）はTensor オブジェクトのプロパティrequires_gradがTrueになっているものである
（xをTensorオブジェクトであるとすると後付けでx.requires_grad_(True)メソッドを使うことでパラメータにすることが可能）
・PyTorchでは演算はtorch.autograd.Functionオブジェクトである（自分の推測）
（感想：ちょっと自動微分がよくわからないので、勉強してみる）
niku自動微分について勉強する
かなり昔
に計算グラフの話が書いてあったはずなので、引っ張り出して再勉強してみる。
「５章 誤差逆伝播法」に該当の情報があるはずなのでここをしっかりと理解しながら読むことにする
5.1.1計算グラフで解く を読む
自分の理解を助けるために、計算グラフの構築ルールをカスタマイズして作成した。
計算グラフ構築のマイルール
- データは長方形で表現
- 演算は丸で表現
- データの流れを矢印で表現（矢印の上にデータの値を記載する）
これに従って、同セクションの問2
「問 2：太郎くんはスーパーでリンゴを 2 個、みかんを 3 個買いました。リンゴは1 個 100 円、みかんは 1個 150 円です。消費税が 10% かかるものとして、支払う金額を求めなさい。」
の計算グラフの構築をきちんとマイルールに則り、手で書いて理解を深める。その様子をprocreateのタイムラプスで作成した結果を乗せる
計算グラフを手書きで構築
このように左から右に普通に計算する方法を順伝播（foward propagation）という
niku自動微分について勉強する（つづき）
5.2.1 計算グラフの逆伝播 を読む
ここが、今のところ最重要ポイント、まずは逆伝播の計算ルールをきっちりと覚えておくこと（何故そうするかの説明は後で出てくるが、ルールを覚えないことにはその説明もままならない）
計算グラフの逆伝播の計算ルール
- 計算グラフのある１つのノードのみに着目する
- そのノードの入力x, 出力yに着目する
- yとxから偏微分
を計算する（というかしておく） - 下流から値
が入力されたら、上流に を出力する
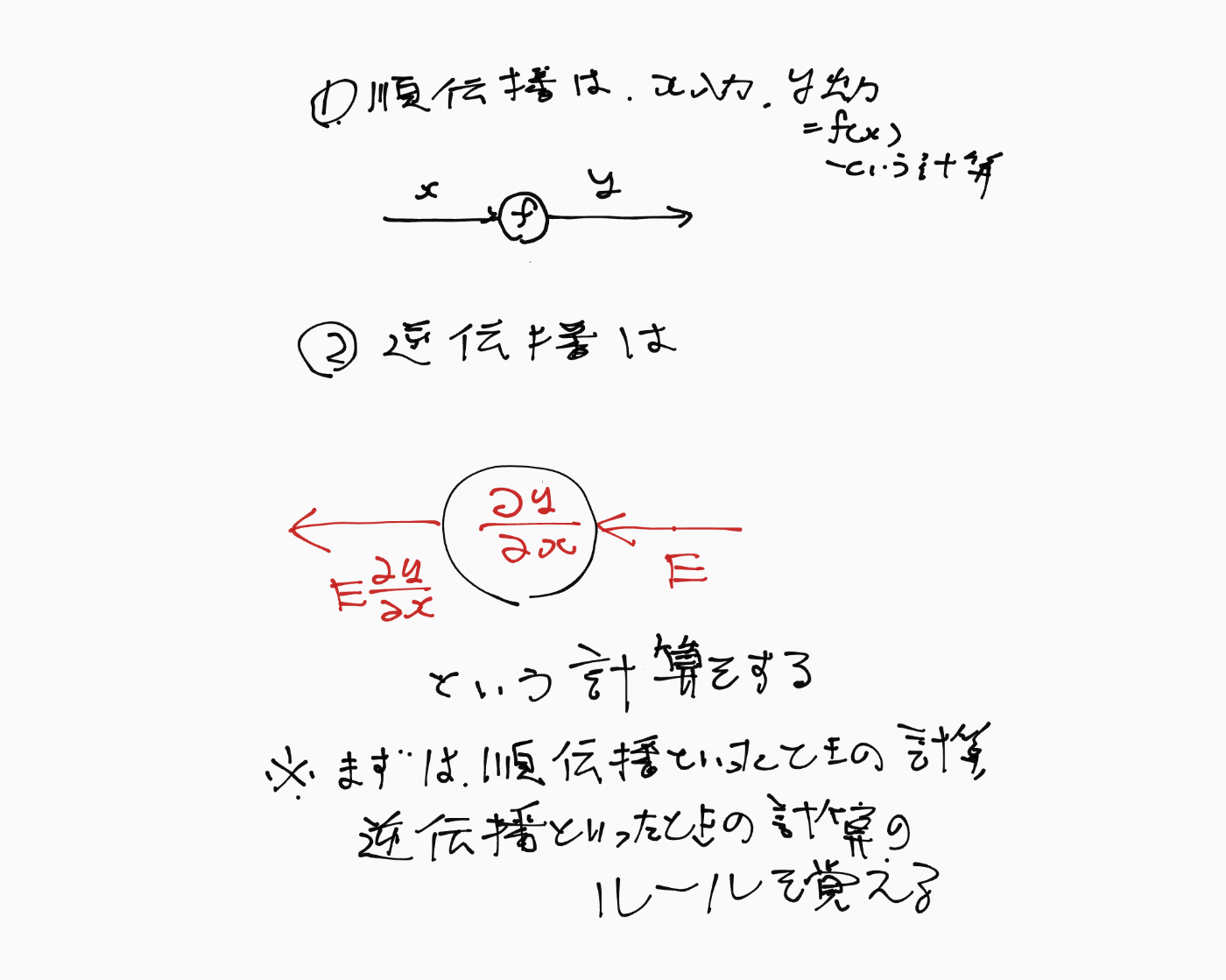
まずは、あるノードに対して順伝播といったときの計算ルールと逆伝播といったときの計算ルールを覚えよう
niku計算グラフの順伝播と逆伝播の理解のための図（要改良）
文字が潰れて読めないしゴチャゴチャしすぎている
niku計算グラフの順伝播と逆伝播の理解のための図ver2（要改良）
まあ、でも俺は理解できたしいいか。次に行く
niku計算グラフのことがここまで理解できれば
を再度読んでピンと来るようになるだろう。
明日からもう一度チャレンジ
自動微分ってのは、多分
１．計算グラフ各ノード順伝播（forward関数）計算時に逆伝播（backward関数）計算に必要なパラメータを記憶しておく
２．あとは計算グラフ逆伝播計算ルールに従って計算することで連鎖律により学習に必要な微分係数が算出できる
ってこと
nikuに戻る
Tensors, Functions and Computational graphを読む のつづき
Tensorオブジェクトは逆伝播計算用にgrad_fnという関数のレファレンスを保持している。
nikuComputing Gradients を読む
損失関数をlossとして、その微分係数を算出するには
- loss.backward() という関数を呼び出す
- 学習可能なTensorとしてw, bがあるとすると、そのgradプロパティが、微分係数となる
例：
loss.backward()
print(w.grad)
print(b.grad)
nikuDisabling Gradient Tracking を読む
計算の高速化やパラメータの固定化のために
Tensorオブジェクトの勾配計算を無効化できる。
方法１：
with torch.no_grad():
を使う
例：
with torch.no_grad():
z = torch.matmul(x, w)+b
方法２：
detach()
を使う
例：
z_det = z.detach()
PackedSequenceについて
PackedSequenceは長さの異なるシーケンスのリストをpack_sequenceメソッドに入力して作成する。
PackedSequenceが所持する情報から、元のシーケンスを再現したり、パディングしたシーケンスを構築したりするための理解を目指す
まずはPackedSequenceを生成するための長さが不揃いのシーケンスのリストを作成表示する
from torch.nn.utils.rnn import pack_sequence, pad_packed_sequence
import torch
a = torch.tensor([1,2,3])
b = torch.tensor([4,5])
c = torch.tensor([6])
d = torch.tensor([7,8,9])
e = torch.tensor([10])
input_data = ([a,b,c,d,e])
print(input_data)
[tensor([1, 2, 3]), tensor([4, 5]), tensor([6]), tensor([7, 8, 9]), tensor([10])]
長さが3,2,1,2,3のシーケンスのリストができていることがわかる
それぞれの名前をa,b,c,d,eとする
packed = pack_sequence(input_data, enforce_sorted=False)
print(packed)
PackedSequence(data=tensor([ 1, 7, 4, 6, 10, 2, 8, 5, 3, 9]), batch_sizes=tensor([5, 3, 2]), sorted_indices=tensor([0, 3, 1, 2, 4]), unsorted_indices=tensor([0, 2, 3, 1, 4]))
PackedSequenceのdataは、元のシーケンスの要素が並んでいそうであることがわかる、データ自体はあるので後は残りの情報からいかにして、復元できるか規則性を観察する
まずは、batch_sizesに着目して観察してみる、
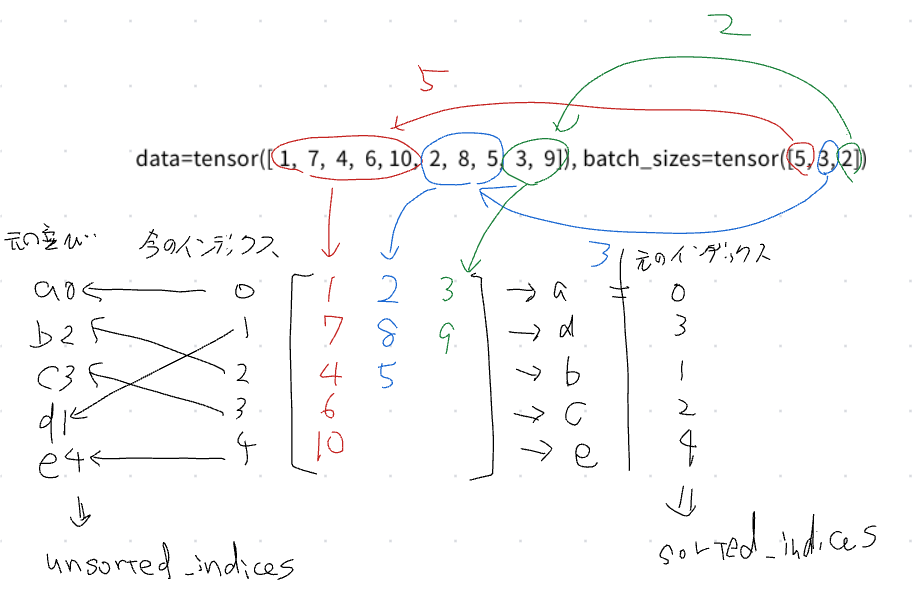観察した結果
再現のためのステップ
Step1. batch_sizesのindex=0の値分だけ、dataから要素を取り出し、列ベクトルとして並べる
Step2. batch_sizesのindex=1の値分だけ、dataからStep1の続きから要素を取り出し、列ベクトルとして並べる
Step3.batch_sizesのindex=2の値分だけ、dataからStep2の続きから要素を取り出し、列ベクトルとして並べる
これで、長さの異なるシーケンスの元データが復元できる、さらのunsorted_indicesを使って、各シーケンスを並び替えるとa,b,c,d,eの並びになってめでたしめでたし
nikuパラメータと勾配を可視化したい
まずは、ここを写経する
niku基礎からきっちりと学び直す
作ったモデルが発散してるのかなんなのかNaNを吐き出すので、これを何とかするために勾配だのパラメータだのを可視化する方法をきっちりと基礎から理解することにした。
まずはJupyter Notebookをノートとして使うための基本
Jupyter 自体のモード：コマンドモードとエディットモードの切り替え方法
JupyterのCellのモード：MarkdownモードとCodeモードの切り替え方法
自分用理解（自分定義用語あり）
なぜPytorchのforward演算とbackward演算の知識が必要なのか私見
うまく利用するためにPytorchをどう捉えて置くべきか（私見）
nikuPyTorchの使い方になれるための復習用コード（Pytorchを使う前に写経）
# まずは、バックプロパゲーションを可能たらしめる部分の知識復習コード
import torch
x = torch.tensor(5.0, requires_grad=True)
y = x**2
# backward()を実行していないのでgrad（勾配）がない（None）
print(x.grad)
print(y)
# grad_fnこそがbackward()計算の要
print(y.grad_fn)
# grad_fnはnext_functionsという、forward()実行時途中経過で生成されたTensorのgrad_fnのタプルを持つ（これがバックプロパゲーション可能たらしめる）
print(y.grad_fn.next_functions)
# 当然最終的には更新可能パラメータ用Tensorにいきつく（variableをもつgrad_fn）
print(y.grad_fn.next_functions[0][0].variable)
# gradはbackward()実行時に生成・積算される
y.backward()
print(x.grad)
# gradはzero_()を実行しないとリセットされない
x.grad.zero_()
print(x.grad)
# 手動パラメータ更新で勾配降下法（Gradient Descent）を実行し理解を深める
import torch
lr = 0.001
x = torch.tensor(5.0, requires_grad=True)
y = x**2
print(y)
y.backward()
x.data -= lr * x.grad.data
x.grad.zero_()
y = x**2
print(y)
# backward()実行するTensorはその都度生成する必要がある※backward()は1回のTensor生成につき1回しかできない
y.backward()
x.data -= lr * x.grad.data
x.grad.zero_()
y = x**2
print(y)
# 繰り返しと関数を使ってパラメータ更新をする
import torch
def forward(x0, x1):
y = x0**2 + x1**2
return y
x0 = torch.tensor(5.0, requires_grad=True)
x1 = torch.tensor(3.0, requires_grad=True)
iters = 10000
lr = 0.001
y = forward(x0,x1)
y.backward()
x0.data -= lr * x0.grad.data
x1.data -= lr * x1.grad.data
for i in range(iters):
if i % 1000 == 0:
print(y, x0.item(), x1.item(), x0.grad.item(), x1.grad.item())
x0.grad.zero_()
x1.grad.zero_()
y = forward(x0,x1)
y.backward()
x0.data -= lr * x0.grad.data
x1.data -= lr * x1.grad.data
print(y, x0.item(), x1.item(), x0.grad.item(), x1.grad.item())
# パラメータ更新を一括で行うためにnn.Module, torch.optimを使う
import torch
import torch.nn as nn
import torch.nn.functional as F
torch.manual_seed(0)
x = torch.rand(100,1)
y = torch.sin(2*torch.pi*x) + 0.1*torch.rand(100,1)
# 計算モデルとしてのクラス定義（nn.Module継承）（演算要素をメンバ変数として生成し、forwardでgrad_fnを持つTensor生成）
class Model(nn.Module):
def __init__(self, input_size=1, hidden_size=2, output_size=1):
super().__init__()
self.linear1 = nn.Linear(input_size, hidden_size)
self.linear2 = nn.Linear(hidden_size, output_size)
def forward(self, x):
y = self.linear1(x)
y = F.sigmoid(y)
y = self.linear2(y)
return y
# 学習率（発散しないように）
lr = 0.2
iters = 100000
# 計算モデルのインスタンス生成
model = Model()
# 一括更新のためtorch.optimを生成（計算モデル内で一括更新したいパラメータのリストをmodel.parameters()で入力）
optimizer = torch.optim.SGD(model.parameters(), lr=lr)
# 繰り返し学習（パラメータ勾配の一括リセットを利用 optimizer.zero_grad()）（パラメータの一括更新を利用optimizer.step()）
for i in range(iters):
y_pred = model(x)
loss = F.mse_loss(y, y_pred)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if i % 10000 == 0:
print(loss.item())
print(loss.item())
import matplotlib.pyplot as plt
plt.scatter(x.detach().numpy(), y.detach().numpy(), s=10)
x = torch.linspace(0, 1, 100).reshape(-1,1)
print(x.shape)
y = model(x).detach().numpy()
plt.plot(x,y,color='red')
plt.show()
nanがでないように注意
以下のURLでnanが出るケースを熟知すること
そもそも使用するデータセットにnanが含まれていないか確認すること
i = 0
for d in ds:
if torch.any(torch.isnan(d)):
print(i, d)
i+=1
長きにわたるnanとの戦いが終わったので次へ
とりあえず、VAEの理論と実装を自在にこなせるくらいになるのを目標にする