こんにちはみなさん。
気が付けば高校数学からベクトルが消えつつあるということで、「え、まじで言ってる?」状態なわけですが、一方でエンジニアの仕事の中ではたまにポロっと「ベクトル」「コサイン類似度」「規格化」みたいな用語が出てくるわけで、この辺の理解が今後さらにばらついてくるのかなぁと思った次第。
そこで、簡易的ではありますが、ベクトルと内積について軽くまとめながら、n次元系のベクトルまで拡張して考えて、現在の機械学習やらなんやらの話に追いつきやすくしていければいいかなと思いました。
ベクトル
ベクトル周りの基礎的な部分を見ていきます。
ベクトル
ベクトルとは何かというと、方向と大きさを持った量のことです。要するに矢印です。
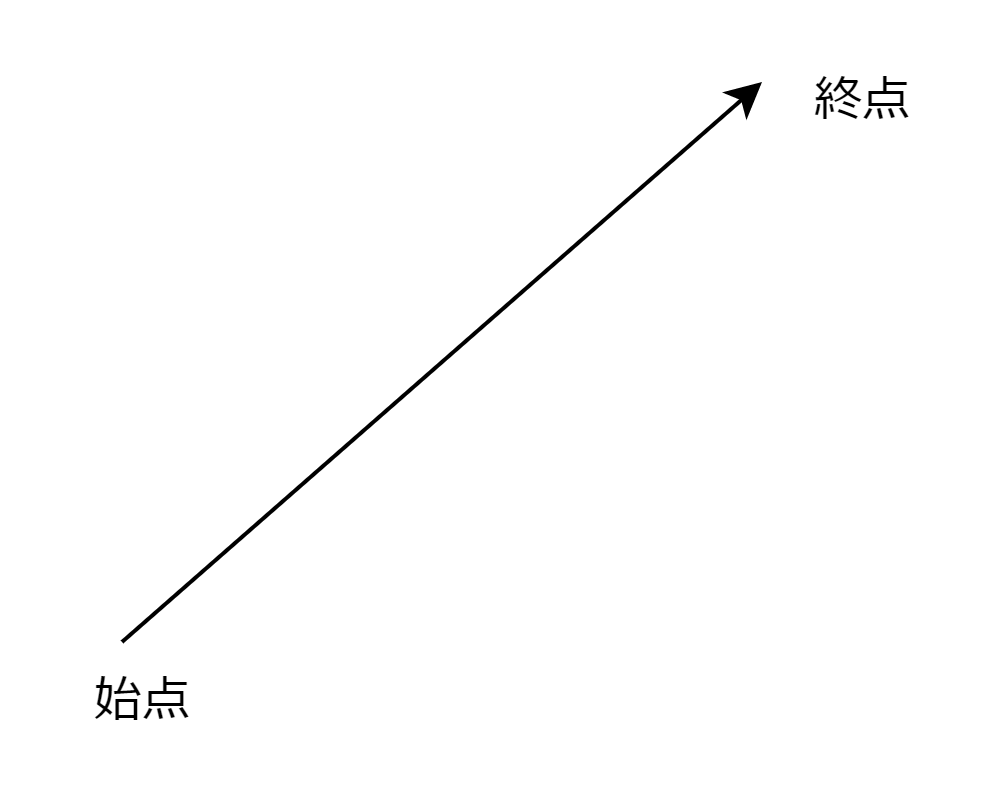
ベクトルであることがわかるために、変数がベクトルであるときは、慣例的に\vec{a}みたいに頭に矢印を書いたり\bm{a}みたいに太文字にして書きます。この記事では太文字\bm{a}で書くことにします。
また、ベクトルの根元を始点、ベクトルの矢印の先端を終点と呼びます。
ベクトルの足し算
ベクトルの足し算は、一方のベクトル\bm{a}の終点に、他方のベクトル\bm{b}の始点を合わせ、その終点に向けて\bm{a}の根元から矢印を書くことで定義します。また、二つのベクトルの始点を合わせ、出来上がった平行四辺形の対角線上の角に向けて両ベクトルの始点から矢印を書くことでも定義できます。両者は意味的には同じです。

スカラー倍
ベクトル\bm{a}に対し、0以上の数値\alphaをかけたベクトル\alpha\bm{a}は方向が同じで、長さだけが\alpha倍されたベクトルとして定義します。
一方ベクトル\bm{a}に対し、-1をかけたベクトル(-1)\bm{a} = -\bm{a}を逆ベクトルと呼び、長さが同じで方向だけが\bm{a}の反対方向を向いたベクトルとして定義します。
その他の性質
ここまではベクトルとその演算の定義です。なので、「そういうもんだ」と覚えてください。この性質から導けるいくつかの性質を見ていきます。
ベクトルの引き算
ベクトルの引き算は次のように逆ベクトルの足し算と読み替えることができます。
\bm{c} = \bm{a} - \bm{b} = \bm{a} + (-\bm{b})

ベクトルの分解
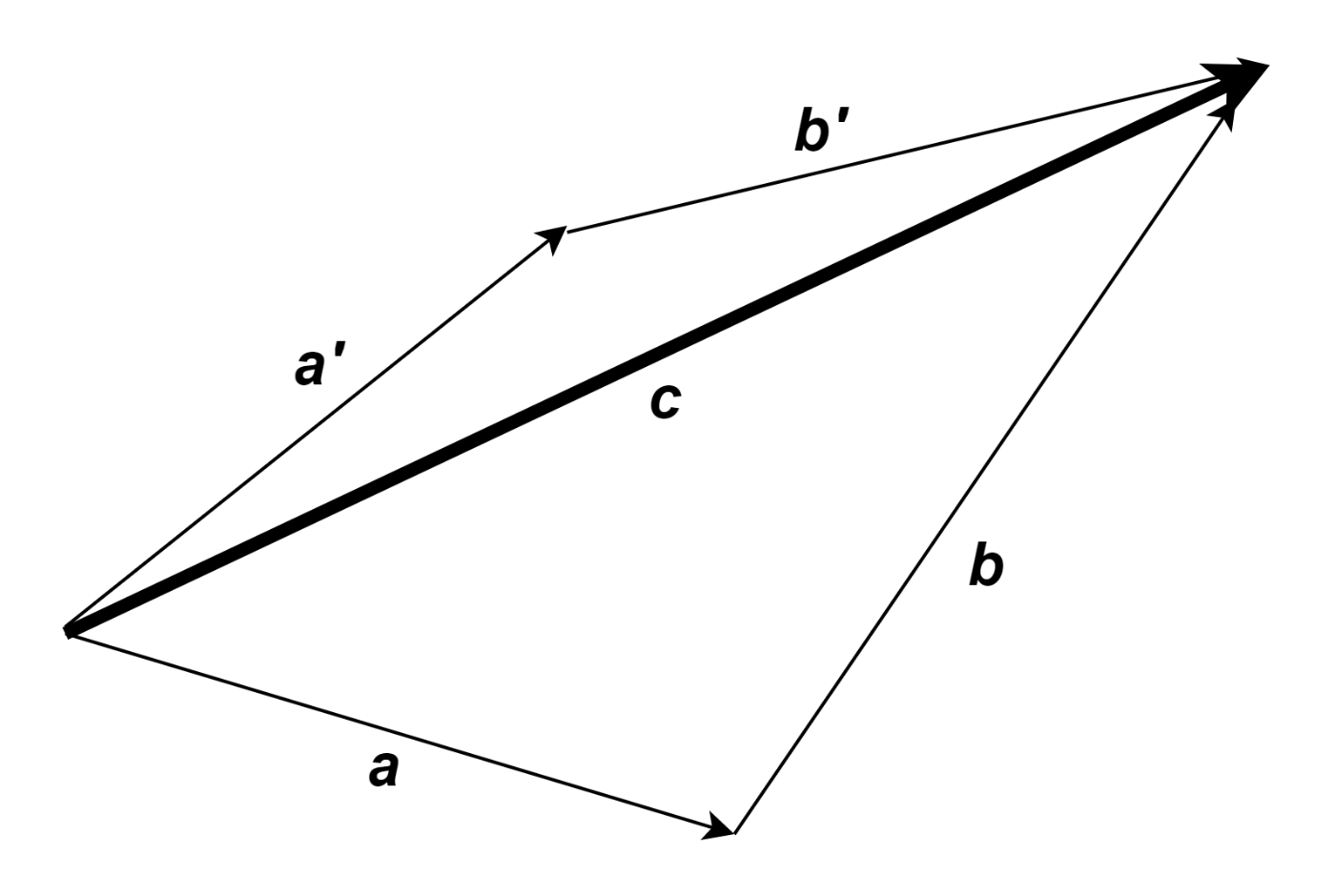
ベクトルは別の複数個のベクトルの足し算の結果として表現できます。これがベクトルの分解です。ベクトルを別の扱いやすいベクトルの足し算で表すのは、今後使用する超重要なテクニックになります。
\bm{c} = \bm{a} + \bm{b} = \bm{a}' + \bm{b}'
スカラー倍の分配則
スカラー倍の分配則は次のようなものです。
\bm{c} = \bm{a} + \bm{b} ~~~~ => ~~~~ \alpha\bm{c} = \alpha(\bm{a} + \bm{b}) = \alpha\bm{a} + \alpha\bm{b}
要するに、足し算全体をスカラー倍したものと、足し算の中の個々のベクトルをスカラー倍してから足したものは等しくなるというものです。
これらの性質は今後よく出てきます。
ベクトルの内積
ベクトル自体の定義が終わりましたので、次はベクトルの内積を定義します。ベクトルの内積とそこから導かれる性質を簡単に理解しましょう。
ベクトルの内積
二つのベクトル\bm{a}, \bm{b}の内積は次のように定義します。
\bm{a} \sdot \bm{b} = |\bm{a}||\bm{b}|\cos \theta
ここで、|\bm{a}|はベクトル\bm{a}の長さを表し、\thetaは二つのベクトルの始点を合わせたときの角度になります。

三角比の詳しい説明はしませんが、|\bm{b}|\cos \thetaというのは、両者のベクトルの始点を合わせたうえで、ベクトル\bm{b}の終点からベクトル\bm{a}を含む直線上に向けて垂線を下し、その交点を終点としたベクトルの長さになります。
これは内積の定義なので、基本的にそういうもんだと思ってください。
内積の分配則
ベクトルの内積にも分配則があります。ベクトル\bm{c}, \bm{d}に対し、
\bm{c} = \bm{a} + \bm{b} ~~~~ => ~~~~ \bm{d} \sdot \bm{c} = \bm{d} \sdot (\bm{a} + \bm{b}) = \bm{d} \sdot \bm{a} + \bm{d} \sdot \bm{b}
これは次の図を考えたとき、\bm{a}と\bm{d}のなす角\theta_a、\bm{b}と\bm{d}のなす角を\theta_bとすると

|\bm{c}|\cos\theta = |\bm{a}|\cos\theta_a + |\bm{b}|\cos\theta_b
が成立していることから導かれます。
内積の値と直交
二つのベクトルのなす角\thetaは0^{\circ}から180^{\circ}の値をとります。二つのベクトルの大きさを固定し、角度を変化させていきましょう。そうすると次の式のようになります。
\bm{a}\sdot\bm{b} = \left\lbrace \begin{array}{cc}
|\bm{a}||\bm{b}| & (\theta = 0) \\
|\bm{a}||\bm{b}|\cos\theta & (0 < \theta < 90) \\
0 & (\theta=90) \\
-|\bm{a}||\bm{b}|\cos(180 - \theta) & (90 < \theta < 180) \\
-|\bm{a}||\bm{b}| & (\theta = 180)
\end{array}
\right.
こんな感じです。
直交
\theta=90で\cos\theta = 0になりますので、内積も0になります。大きさがゼロではない二つのベクトルの内積が0の時、この二つのベクトルは直交しているといいます。この直交の概念も次で使います。
ベクトルの大きさと内積
内積の定義は \bm{a}\sdot\bm{b}=|\bm{a}||\bm{b}|\cos\thetaですが、ここで自分自身との内積をとるとどうなるでしょうか。
\bm{a}\sdot\bm{a}=|\bm{a}||\bm{a}|\cos0 = |\bm{a}|^2
となります。つまり、ベクトルの自分自身との内積は、そのベクトルの大きさの2乗の値に等しくなります。
ベクトルの成分表示
ここではベクトルの成分表示について解説します。
これまでは矢印をいちいち書いて考えてきましたが、これはこれで面倒です。そこで、ベクトルを複数の数字の組で表現できるようになると楽になります。というわけで、これまでのベクトルの概念を使って、成分表示をしていきましょう。
単位ベクトルと分解
大きさが1のベクトルを単位ベクトルと呼びます。慣例的に\bm{e}と書きます。今、あるベクトル\bm{x}を直交する二つの単位ベクトル\bm{e}_1, \bm{e}_2を使って分解してみます。

これにより、\bm{x}は
\bm{x} = x_1\bm{e}_1 + x_2\bm{e}_2
と書けます。
2次元系と成分表示
仮にこの直交する二つの単位ベクトルを使って、あらゆるベクトルを分解できるとき、その系は2次元系であるといいます。
また、2次元系においては、直交する単位ベクトルを決めてしまえば、すべてのベクトルはその単位ベクトルの係数x_1, x_2によって一意に決まります。そこで、次のように単位ベクトルを書くのを省略して、数値の組だけでベクトルを表現することができ、これを成分表示と呼びます。
\bm{x} = x_1\bm{e}_1 + x_2\bm{e}_2 \equiv (x_1, x_2)
最後の\equivは、「そのように定義する」という意味で見てください。
成分表示の内積
ベクトルを成分表示できましたので、これの内積を求めてみましょう。2つのベクトル\bm{x}, \bm{y}に対し、
\bm{x} = (x_1, x_2) \\
\bm{y} = (y_1, y_2)
のように成分表示できていたとすると、その内積は、少し前に解説した分配則を使い、
\begin{aligned}
\bm{x}\sdot\bm{y} &= (x_1\bm{e}_1 + x_2\bm{e}_2) \sdot (y_1\bm{e}_1 + y_2\bm{e}_2) \\
&= x_1y_1\bm{e}_1\sdot\bm{e}_1 + x_1y_2\bm{e}_1\sdot\bm{e}_2 + x_2y_1\bm{e}_2\sdot\bm{e}_1 + x_2y_2\bm{e}_2\sdot\bm{e}_2
\end{aligned}
のようになります。
ここで、単位ベクトルと内積の性質から、\bm{e}_1\sdot\bm{e}_1 = |\bm{e}_1|^2 = 1となり、二つの単位ベクトルが直交しているという前提から、\bm{e}_1\sdot\bm{e}_2=\bm{e}_2\sdot\bm{e}_1=0となりますので、結局は
\bm{x}\sdot\bm{y} = x_1y_1 + x_2y_2
となります。
その他の性質
成分表示したベクトルの大きさ
これも少し前に解説しましたが、自分自身との内積をとると、そのベクトルの大きさの2乗になります。
そこで、成分表示したベクトルの自分との内積を計算すると、
\bm{x} = (x_1, x_2) \\
|\bm{x}|^2 = \bm{x}\sdot\bm{x} = x_1x_1 + x_2x_2 = x_1{}^2 + x_2{}^2
となります。
単位ベクトルの成分表示
単位ベクトルも成分表示でき、\bm{e}_1 = 1\bm{e}_1 + 0\bm{e}_2 = (1, 0)と書けます。おなじように\bm{e}_2=(0, 1)となります。
成分表示まとめ
- 2つの直交する単位ベクトルですべてのベクトルが構成できる系を2次元系と呼ぶ
- 2次元系において、ベクトル\bm{x}=(x_1, x_2)のように成分表示することができる。
- 2次元系におけるベクトルの内積は、成分表示を使って以下のように表現できる
\bm{x} = (x_1, x_2), \bm{y} = (y_1, y_2) \\
\bm{x}\sdot\bm{y} = x_1y_1 + x_2y_2
- 2次元系におけるベクトルの大きさは、成分を用いて、|\bm{x}|^2 = x_1{}^2 + x_2{}^2である。
高次元ベクトルの成分表示と内積
2次元系では2つの直交する単位ベクトルですべてのベクトルを表現できていました。しかし、これは平面上のような限られた系に限ります。
我々が取り組む系によっては2つの単位ベクトルでは足りず、3つやそれ以上の単位ベクトルで構成されたベクトルを相手にする必要があります。そこで、ここからはもっと次元の大きな系のベクトルの成分表示について解説します。
数式が多くなるので大変かもしれませんが、これまでのベクトルの定義や内積の定義は一切変わらないので、分からなくなったら初めから読み直してみるといいかもしれません。
n次元系と成分表示
これから2次元、3次元、それ以上の次元をまとめて扱いたいので、まず一般化しましょう。
nは自然数とし、直交するn個の単位ベクトルを使ってすべてのベクトルを分解できるとき、その系はn次元系といいます。
n個の直交する単位ベクトルは内積について次のように書けます。
\bm{e}_i\sdot\bm{e}_j = \left\lbrace
\begin{array}{cc}
0 & (i \neq j) \\
1 & (i = j)
\end{array}
\right. (1 <= i, j <= n)
この単位ベクトルを使って、ベクトル\bm{x}を次のように表します。
\begin{aligned}
\bm{x} &= x_1\bm{e}_1 + x_2\bm{e}_2 + x_3\bm{e}_3 + ... + x_n\bm{e}_n \\
&= \sum_{i=1}^n x_i\bm{e}_i
\end{aligned}
あらゆるベクトルはこのn個の単位ベクトルの和で表せるので、2次元の時と同様にn個の数値の組による成分表示が可能です。
\begin{aligned}
\bm{x} &= \sum_{i=1}^n x_i\bm{e}_i \\
& \equiv (x_1, x_2, ..., x_n)
\end{aligned}
こんな感じです。
n次元ベクトルの成分表示の性質
成分表示したn次元のベクトル(x_1, x_2, ..., x_n)について、内積周りの性質を見ていきます。
内積
内積の計算をしていきます。2次元の時と同じで、分配則を利用して計算することになります。ゴツめの計算が出てきますが、いったん我慢してください。
\bm{x} = (x_1, x_2, ..., x_n)\\
\bm{y} = (y_1, y_2, ..., y_n)\\
\begin{aligned}
\bm{x}\sdot\bm{y} &= \left(\sum_{i=1}^nx_i\bm{e}_i\right)\sdot\left(\sum_{j=1}^ny_j\bm{e}_j\right) \\
&= \sum_{i=1}^n\sum_{j=1}^n x_iy_j\bm{e}_i\sdot\bm{e}_j
\end{aligned}
2重の\sum_{}^{}が出てきてなかなか厄介そうに見えます。最後の式を展開するとn^2個の項が出てきて一見すると大変です。
x_1y_1\bm{e}_1\sdot\bm{e}_1 + x_1y_2\bm{e}_1\sdot\bm{e}_2 + x_1y_3\bm{e}_1\sdot\bm{e}_3 + ... + x_1y_n\bm{e}_1\sdot\bm{e}_n + x_2y_1\bm{e}_2\sdot\bm{e}_1 + ... + x_ny_n\bm{e}_n\sdot\bm{e}_n
しかし、先に直交する単位ベクトルの性質として、\bm{e}_i\sdot\bm{e}_j = 0 (i\neq j)という性質があったのを思い出しましょう。すると、上の式の中で、i\neq jとなっている部分は0となって消えます。
結局、最終的な内積の値は
\bm{x}\sdot\bm{y} = x_1y_1 + x_2y_2 + ... + x_ny_n = \sum_{i=1}^n x_iy_i
ベクトルの大きさ
成分表示したn次元のベクトルの大きさの2乗は自分自身の内積に等しいので、
|\bm{x}|^2 = \bm{x}\sdot\bm{x} = x_1x_1 + x_2x_2 + ... + x_nx_n = \sum_{i=1}^n x_i{}^2
まとめ
- n次元系とはすべてのベクトルがn個の直交した単位ベクトルを使って分解できる系のことである
- n次元系のベクトルはn個のパラメータ(x_1, x_2, ..., x_n)で表現できる
- n次元系のベクトル\bm{x}, \bm{y}の内積は成分表示をした以下のようになる。
\bm{x} = (x_1, x_2, ..., x_n)\\
\bm{y} = (y_1, y_2, ..., y_n)\\
\bm{x}\sdot\bm{y} = x_1y_1 + x_2y_2 + ... + x_ny_n = \sum_{i=1}^n x_iy_i
- n次元系のベクトルの大きさは|\bm{x}|^2 = \sum_{i=1}^nx_i{}^2になる。
おまけ - コサイン類似度
内積の定義は\bm{x}\sdot\bm{y} = |\bm{x}||\bm{y}|\cos\thetaでした。ここでの\thetaは、二つのベクトル\bm{x}, \bm{y}のなす角だったわけですが、この角度が小さいほど向いている方向が近いことになります。そこで、この角度が小さいほど方向が近い = 似ているとみなし、\thetaの値が小さいほど\cos\thetaの値が大きくなることを利用して、\cos\thetaの値をコサイン類似度という仰々しい名前を付けているわけです。
一般化したn次元のベクトルのコサイン類似度は成分表示した場合、以下のようになります。
\bm{x} = (x_1, x_2, ..., x_n)\\
\bm{y} = (y_1, y_2, ..., y_n)\\
~~~~ \\
\begin{aligned}
\cos\theta &= \dfrac{\bm{x}\sdot\bm{y}}{|\bm{x}||\bm{y}|}
&= \dfrac{\displaystyle \sum_{i=1}^n x_iy_i}{\displaystyle \left( \sqrt{\sum_{i=1}^n x_i{}^2}\right)\left(\sqrt{\sum_{i=1}^n y_i{}^2}\right)}
\end{aligned}
便利なシステムだと、ベクトルの大きさがはじめから1に規格化している場合があるため、その場合は大きさの計算が省略できて、
\cos\theta = \sum_{i=1}^n x_iy_i
というとんでもなく簡単な数式になります。ここまでくるとプログラムも簡単で、例えば次のような簡単な配列の計算で完結できます。
$dotProduct = 0;
foreach ($vec1 as $key => $val) {
$dotProduct += $val * $vec2[$key];
}
return $dotProduct;
まとめ
というわけで、ベクトルの定義から内積、成分表示を一通り駆け抜けました。最近は機械学習とかでベクトルとか類似度の話とかがよく出てくるというのに、高校の数学でベクトルが数学Cに移動し、文系の人がほとんど触れなくなっちゃったということらしいので、文系の人も一定数くるようなIT業界でこの話知らないのは危ないかなと思って書きました。
分からないところや、間違っているところがあれば指摘お願いします。







Discussion