🦔
【paiza】マラソン形式コンテストに初参加してみた【Sランク暗黒の地】

2025/09/17に公開
最近、「エンジニア騎士とクエリの魔女」というゲームを始めてみました。

https://paiza.jp/code_and_sql/

そこで様々な難易度のプログラム問題に取り組めるのですが、そこのSランク問題がマラソン形式でした。
今まで競技プログラミング系の問題には取り組んだことがあったのですが、マラソン形式は初めてだったので、その時の記録を書いていきます。
2025/09/16時点で正解者193人中8位になれました。


 0. 問題平らな板の表面に N 本の釘が、頭部を少し浮かせた状態で打ち込まれています。

あなたは、これらの釘に 1 本の長い紐を掛けて模様を作ることにしました。
各釘はそれぞれ 1 から N の異なる数で番号付けられており、互いに区別することができます。

あなたは、この番号を利用して、以下の手順 1 から 3 に従って紐を掛けてみました。
まず、 1 番目の釘に紐の端を固定する。
次に、 2, ..., N の順番で釘に紐を掛ける。
最後に、 N 番目の釘の位置で紐を切断し固定する。
しかし、あなたは出来上がった模様を見ても満足できませんでした。

なぜならば、模様に紐の交差ができてしまっていたからです。
付近を探索したところ、新しい釘を K 本だけ見つけました。

そこで、いくつかの釘を追加で打ち込み、それらを中継点とすることで模様を作りなおすことにしました。

すなわち、以下のルールを追加して、上記の手順で改めて紐を掛けなおします。
・手順 1 の前に、板に最大 K 本の釘を打ち込む。ただし、複数の釘が同じ位置にあるような打ち込み方はできない。

・手順 2 において、新たに打ち込んだ釘にはいつ紐を掛けてもよい。

・出来上がった模様において、各釘にちょうど 1 回だけ紐が掛かっているようにする。
所持している紐は十分に長いですが、あなたはなるべく短い紐を使い、紐の交差をなるべく避けた模様を作りたいと考えています。

しかし、釘の配置によっては紐の交差をなくすことができないかもしれません。

そのため、使う紐の長さが短く、交差が少ない模様ほど良いとします。
どのようにすれば良い模様が作れるでしょうか。

ここで、釘は 2 次元平面における点、紐は点と点を結ぶ線分の連結によって表すことができるとします。
要約すると、
1~N番の釘が打たれていて、それらを繋ぐ順番は変えられない
釘と釘を繋ぐ紐の間に新しい釘を打って経路の形を変えることができる
新しい釘を打って、なるべく交点を無くして、かつ短くしたい

という感じの問題ですね。
もう少し複雑な例を示します。


 0-1. スコア計算式スコアの計算式は以下の通りです。
(入力された配置での紐の長さ + 入力された配置の交差回数 × 50) - (出力された配置での紐の長さ + 出力された配置の交差回数 × 50)

ただし、マイナスの値になった場合は 0 として扱います。
紐が多少長くなるより、交点を無くしたほうが得点が高いようですね。

 0-2. 制約すべてのテストケースにおいて、以下の条件をみたします。

・2 ≦ N ≦ 1,000

・1 ≦ K ≦ min(1,000, 2N)

・0 ≦ x_i, y_i ≦ 1000 (1 ≦ i ≦ N)

　・i ≠ j (1 ≦ i, j ≦ N) のとき x_i ≠ x_j または y_i ≠ y_j
それでは解法を考えていきます。
開発手法としては、AI(Gemini 2.5 Pro)と相談しながら開発しました。

 1. 端点探索1例図を見ていて考えついたのがこれです。

交点について、それぞれの線分の端点周辺に追加の釘を置いたら迂回できそうですよね。



このアルゴリズムだけで4通りの迂廻路ができます。

結局これ以上良い案は思いつかず、最後までこのアルゴリズムで勝負することになりました。

 1-1. ヘルパー関数では端点探索のアルゴリズムを作成する上で必要となるヘルパー関数を作成します。

線分同士が交差しているか、線分の長さを求めたりする関数ですね。
public static long CrossLl(long x1, long y1, long x2, long y2) => x1 * y2 - y1 * x2;
public static long Cross(P a, P b, P c) => CrossLl(b.X - a.X, b.Y - a.Y, c.X - a.X, c.Y - a.Y);
public static int SgnLl(long v) => v > 0 ? 1 : (v < 0 ? -1 : 0);

public static bool SegIntersectStrict(P a, P b, P c, P d)
{
	if (Math.Max(a.X, b.X) < Math.Min(c.X, d.X) || Math.Max(c.X, d.X) < Math.Min(a.X, b.X) ||
		Math.Max(a.Y, b.Y) < Math.Min(c.Y, d.Y) || Math.Max(c.Y, d.Y) < Math.Min(a.Y, b.Y))
	{
		return false;
	}
	long c1 = Cross(a, b, c), c2 = Cross(a, b, d), c3 = Cross(c, d, a), c4 = Cross(c, d, b);
	return (c1 > 0 && c2 < 0 || c1 < 0 && c2 > 0) && (c3 > 0 && c4 < 0 || c3 < 0 && c4 > 0);
}

public static (double x, double y) IntersectionPoint(P a, P b, P c, P d)
{
	double A1 = b.Y - a.Y, B1 = a.X - b.X, C1 = A1 * a.X + B1 * a.Y;
	double A2 = d.Y - c.Y, B2 = c.X - d.X, C2 = A2 * c.X + B2 * c.Y;
	double det = A1 * B2 - A2 * B1;
	double x = (B2 * C1 - B1 * C2) / det;
	double y = (A1 * C2 - A2 * C1) / det;
	return (x, y);
}

public static double Dist(P a, P b)
{
	double dx = a.X - b.X, dy = a.Y - b.Y;
	return Math.Sqrt(dx * dx + dy * dy);
}

public static int TotalCrossings(List<P> pts, List<int> path)
{
	int L = path.Count;
	int cnt = 0;
	for (int i = 0; i < L - 1; i++)
	{
		for (int j = i + 2; j < L - 1; j++)
		{
			int ai = path[i], aj = path[i + 1], bi = path[j], bj = path[j + 1];
			if (SegIntersectStrict(pts[ai - 1], pts[aj - 1], pts[bi - 1], pts[bj - 1])) cnt++;
		}
	}
	return cnt;
}

public static int CalculateCrossingDelta(List<P> pts, List<int> path, int segPosToChange, P newNailS)
{
	int L = path.Count;
	if (segPosToChange < 0 || segPosToChange + 1 >= L) return 0;

	int p1Idx = path[segPosToChange];
	int p2Idx = path[segPosToChange + 1];
	P P1 = pts[p1Idx - 1];
	P P2 = pts[p2Idx - 1];

	int removed = 0, added = 0;

	for (int i = 0; i < L - 1; ++i)
	{
		if (i == segPosToChange) continue;

		int op1Idx = path[i];
		int op2Idx = path[i + 1];
		P OP1 = pts[op1Idx - 1];
		P OP2 = pts[op2Idx - 1];

		if (SegIntersectStrict(P1, P2, OP1, OP2)) removed++;
		if (SegIntersectStrict(P1, newNailS, OP1, OP2)) added++;
		if (SegIntersectStrict(newNailS, P2, OP1, OP2)) added++;
	}
	return removed - added;
}

 1-2. 端点探索アルゴリズムそれではメインの端点探索の関数を書いていきます。
public static void AddCandidateIfValid(List<P> allPts, List<int> path, List<Cand> candidates, int segPos, P candP)
{
	if (candP.X < 0 || candP.X > 1000 || candP.Y < 0 || candP.Y > 1000) return;

	foreach (var p in allPts) if (p.X == candP.X && p.Y == candP.Y) return;

	int reduce = CalculateCrossingDelta(allPts, path, segPos, candP);
	if (reduce <= 0) return;

	P P1 = allPts[path[segPos] - 1];
	P P2 = allPts[path[segPos + 1] - 1];
	double deltaLen = Dist(P1, candP) + Dist(candP, P2) - Dist(P1, P2);

	candidates.Add(new Cand
	{
		InsertPos = segPos,
		Coord = candP,
		Reduce = reduce,
		DeltaLen = deltaLen
	});
}

// 候補生成1: 端点+周辺探索
public static void FindCandidatesByEndpoint(List<P> allPts, List<int> path, double intersectionX, double intersectionY, List<Cand> candidates, int segPos, int endpointIndex)
{
	const int Dmax = 15;
	const int searchRadius = 2;

	P pOld = allPts[endpointIndex];
	int dxSign = SgnLl((long)Math.Round(pOld.X - intersectionX));
	int dySign = SgnLl((long)Math.Round(pOld.Y - intersectionY));
	if (dxSign == 0 && dySign == 0) { dxSign = 1; dySign = 1; }

	for (int d = 1; d <= Dmax; d += 2)
	{
		P centerP = new P(pOld.X + dxSign * d, pOld.Y + dySign * d);
		for (int dx = -searchRadius; dx <= searchRadius; ++dx)
		{
			for (int dy = -searchRadius; dy <= searchRadius; ++dy)
			{
				AddCandidateIfValid(allPts, path, candidates, segPos, new P(centerP.X + dx, centerP.Y + dy));
			}
		}
	}
}

 1-3. 貪欲法端点は4通り、周辺探索したらもっとあるので、それらの手を比較して最善手をソートできるようにしましょう。
「考えられる手」をクラスに保存できるようにします。

そのうえで比較関数を実装します。
// 改善候補の手を格納するクラス
public class Cand : IComparable<Cand>
{
	public int InsertPos;     // path のどの位置の後ろに挿入するか
	public P Coord;           // 新しい釘の座標
	public int Reduce;        // この手を打った時の交差減少数
	public double DeltaLen;   // この手を打った時の紐の増加長

	public int CompareTo(Cand other)
	{
		double myImprovement = (this.Reduce * 50.0) - this.DeltaLen;
		double otherImprovement = (other.Reduce * 50.0) - other.DeltaLen;

		// スコア改善量が大きい方を優先
		if (Math.Abs(myImprovement - otherImprovement) > 1e-9)
		{
			return otherImprovement.CompareTo(myImprovement); // 降順
		}
		// ... (改善量が同じなら、既存のルールでOK)
		if (Coord.X != other.Coord.X) return Coord.X.CompareTo(other.Coord.X);
		return Coord.Y.CompareTo(other.Coord.Y);
	}
}
こうすることで貪欲法を行えるようになりました。
// --- 候補生成 ---
FindCandidatesByEndpoint(allPts, path, ip.x, ip.y, candidates, i, bi - 1);
FindCandidatesByEndpoint(allPts, path, ip.x, ip.y, candidates, i, bj - 1);
FindCandidatesByEndpoint(allPts, path, ip.x, ip.y, candidates, j, ai - 1);
FindCandidatesByEndpoint(allPts, path, ip.x, ip.y, candidates, j, aj - 1);
...

if (candidates.Count == 0) break;

// 1. 今回の「最善手」を見つける (比較のため)
candidates.Sort();
Cand bestCand = candidates[0];

// 最終的に選ばれた手を適用
allPts.Add(bestCand.Coord);
path.Insert(bestCand.InsertPos + 1, allPts.Count);
usedK++;
章最初の例図の4通りで言えば、どれも交点が0個なのでより距離が短い1手が選ばれます。

 1-4. メインループ端点探索を繰り返すメインループを書いていきます。
全ての交点に対して端点探索を繰り返して、その中で最善手を適応する
この処理を追加で打てる釘の数だけ繰り返す

という流れですね。
while (usedK < K)
{
	if (TotalCrossings(allPts, path) == 0) break;

	var candidates = new List<Cand>();
	int L = path.Count;

	for (int i = 0; i < L - 1; ++i)
	{
		for (int j = i + 2; j < L - 1; ++j)
		{
			int ai = path[i], aj = path[i + 1], bi = path[j], bj = path[j + 1];
			if (!SegIntersectStrict(allPts[ai - 1], allPts[aj - 1], allPts[bi - 1], allPts[bj - 1])) continue;

			var ip = IntersectionPoint(allPts[ai - 1], allPts[aj - 1], allPts[bi - 1], allPts[bj - 1]);

			FindCandidatesByEndpoint(allPts, path, ip.x, ip.y, candidates, i, bi - 1);
			FindCandidatesByEndpoint(allPts, path, ip.x, ip.y, candidates, i, bj - 1);
			FindCandidatesByEndpoint(allPts, path, ip.x, ip.y, candidates, j, ai - 1);
			FindCandidatesByEndpoint(allPts, path, ip.x, ip.y, candidates, j, aj - 1);
		}
	}

	if (candidates.Count == 0) break;

	candidates.Sort();
	Cand best = candidates[0];

	allPts.Add(best.Coord);
	path.Insert(best.InsertPos + 1, allPts.Count);
	usedK++;
}

 1-5. 実行時間削減理想の動きを求めるあまり、よくよく考えてみたら計算量がとんでもないことになっていましたね。

このまま提出したら、失敗になってしまいました。

ちなみにC++は3秒、C#は5秒で実行時間超過みたいです。

普通に制約に書いてほしい内容です…
簡単にできる対処法としては、最初に見つけた交点を修正するという方法ですね。
bool foundCross = false;
while (usedK < K)
{
	// ...
	for (int i = 0; i < L - 1; ++i)
	{
		for (int j = i + 2; j < L - 1; ++j)
		{
			// 交点を持っていなければcontinue
			
			// 端点探索

			foundCross = true;
			break;
		}
		if (foundCross)
		{
			break; // 外側ループも抜ける
		}
	}

	// 貪欲法
}
これで実行時間はクリアできるようになりました。

この時の公式スコアは9800点(17位)くらいだった気がします。

 2. テストケースとビジュアライザーの作成ここで実際にどれくらいちゃんと動いてくれるか確かめたくなりました。

ですが公式が用意してくれているのは図1のテストケースのみです。
また得点に関しては公式のジャッジを使用するのが最適なのですが、1日に1回しか更新してくれないのであまり使えません。

 2-1. テストケースの生成各パラメータの制約は分かっているので自分で用意することにしましょう。

プログラムで自動生成します。
using System;
using System.Collections.Generic;
using System.IO;
using System.Linq;
using System.Text;

// メインプロジェクトのP構造体を利用
using static Program;

class Generator
{
    static void Main(string[] args)
    {
        try
        {
            var random = new Random();

            // 1. パラメータをランダムに決定
            int n = random.Next(2, 1001); // 2 <= N <= 1000
            int k = random.Next(1, Math.Min(1000, 2 * n) + 1); // 1 <= K <= min(1000, 2N)

            // 2. 重複しないN個の点を生成
            var points = new HashSet<P>();
            while (points.Count < n)
            {
                int x = random.Next(0, 1001); // 0 <= x, y <= 1000
                int y = random.Next(0, 1001);

                points.Add(new P(x, y));
            }

            // 3. ファイルフォーマットに従って文字列を構築
            var sb = new StringBuilder();
            sb.AppendLine($"{n} {k}");
            foreach (var p in points)
            {
                sb.AppendLine($"{p.X} {p.Y}");
            }

            // 4. 出力ファイル名を決定
            string outputDir = @"C:\Users\neko\source\repos\CodeAndSql_Marathon\tools\in";
            Directory.CreateDirectory(outputDir); // フォルダがなければ作成

            int nextFileNum = 0;
            var existingFiles = Directory.GetFiles(outputDir, "*.txt");
            if (existingFiles.Length > 0)
            {
                nextFileNum = existingFiles
                    .Select(f => Path.GetFileNameWithoutExtension(f))
                    .Where(name => int.TryParse(name, out _))
                    .Select(name => int.Parse(name))
                    .Max() + 1;
            }
            string outputFileName = $"{nextFileNum:D4}.txt";
            string outputFilePath = Path.Combine(outputDir, outputFileName);

            // 5. ファイルに書き出し
            File.WriteAllText(outputFilePath, sb.ToString());

            Console.WriteLine($"Successfully generated test case: {outputFilePath}");
        }
        catch (Exception e)
        {
            Console.Error.WriteLine($"An error occurred: {e.Message}");
        }
    }
}
これで様々なテストケースを試せるようになりました。
14 25
12 14
10 13
14 22
27 15
29 21
22 18
22 23
13 29
29 26
15 20
24 15
23 18
28 27
17 24

 2-2. 自動実行このままでは毎回テストケースを入力して、その出力を見て判断する必要があります。
もっと分かりやすいように自動で全てのテストケースを実行して、スコアがどれくらいになるか教えてもらいましょう。
まずメインプログラムの出力先をファイルに変更します。
public static void Main(string[] args)
{
	if (args.Length < 2)
	{
		Solve();
		return;
	}

	string inputFile = args[0];
	string outputFile = args[1];

	// ファイル入出力に切り替え
	using (var reader = new StreamReader(inputFile))
	using (var writer = new StreamWriter(outputFile))
	{
		Console.SetIn(reader);
		Console.SetOut(writer);
		Solve();
	}
}
続いて、出力結果からスコアを計算するプログラムを作成します。
using System;
using System.Collections.Generic;
using System.IO;
using System.Linq;

// メインプロジェクトの型やメソッドを利用する
using static Program;

class Scorer
{
    static void Main(string[] args)
    {
        if (args.Length < 2)
        {
            Console.Error.WriteLine("Usage: Scorer.exe <input_file> <output_file>");
            return;
        }

        string inputFile = args[0];
        string outputFile = args[1];

        try
        {
            // 初期状態のスコアを計算
            var (initialPts, initialPath) = ReadInitialState(inputFile);
            double initialScore = CalculateScore(initialPts, initialPath);

            // 最終状態のスコアを計算
            var (finalPts, finalPath) = ReadFinalState(outputFile, initialPts);
            double finalScore = CalculateScore(finalPts, finalPath);

            // スコアの差分を計算 (0未満は0)
            long finalPoint = (long)Math.Max(0, Math.Round(initialScore - finalScore));

            Console.WriteLine($"Score = {finalPoint}");
        }
        catch (Exception e)
        {
            Console.Error.WriteLine($"Error: {e.Message}");
            Console.Error.WriteLine(e.StackTrace);
        }
    }

    static (List<P> pts, List<int> path) ReadInitialState(string filePath)
    {
        var lines = File.ReadAllLines(filePath);
        var parts = lines[0].Split();
        int n = int.Parse(parts[0]);

        var pts = new List<P>();
        for (int i = 0; i < n; i++)
        {
            parts = lines[i + 1].Split();
            pts.Add(new P(int.Parse(parts[0]), int.Parse(parts[1])));
        }

        var path = Enumerable.Range(1, n).ToList();
        return (pts, path);
    }

    static (List<P> pts, List<int> path) ReadFinalState(string filePath, List<P> initialPts)
    {
        var lines = File.ReadAllLines(filePath);
        int m = int.Parse(lines[0]);

        var allPts = new List<P>(initialPts);
        for (int i = 0; i < m; i++)
        {
            var parts = lines[i + 1].Split();
            allPts.Add(new P(int.Parse(parts[0]), int.Parse(parts[1])));
        }

        var path = new List<int>();
        for (int i = 0; i < initialPts.Count + m; i++)
        {
            path.Add(int.Parse(lines[i + m + 1]));
        }

        return (allPts, path);
    }

    static double CalculateScore(List<P> pts, List<int> path)
    {
        double totalLength = 0;
        for (int i = 0; i < path.Count - 1; i++)
        {
            P p1 = pts[path[i] - 1];
            P p2 = pts[path[i + 1] - 1];
            totalLength += Dist(p1, p2);
        }

        int crossCount = TotalCrossings(pts, path);

        return totalLength + (double)crossCount * 50;
    }
}
では各テストケースにおいてプログラムを実行し、その出力結果をスコア計算プログラムに送り、そのスコアの結果を表示するプログラムを作成します。
import subprocess
import sys
from pathlib import Path

# パスの設定
EXE_PATH = Path("./src/bin/Release/net6.0/CodeAndSql_Marathon.exe")
SCORER_PATH = Path("./CodeAndSql_Marathon.Scorer/bin/Release/net6.0/CodeAndSql_Marathon.Scorer.exe")
IN_DIR = Path("./tools/in")
OUT_DIR = Path("./tools/out")

# 事前にビルドが実行されているか確認
if not EXE_PATH.exists() or not SCORER_PATH.exists():
    print("[ERROR] Executable not found. Please build the projects first by running:")
    print("dotnet build -c Release")
    sys.exit(1)

# 出力フォルダ作成
OUT_DIR.mkdir(exist_ok=True)

total_score = 0

# inフォルダ内のすべてのtxtファイルに対してループ
input_files = sorted(IN_DIR.glob("*.txt"))
if not input_files:
    print(f"[INFO] No input files found in {IN_DIR}")
    sys.exit(0)

for input_file in input_files:
    case_name = input_file.stem
    output_file = OUT_DIR / f"{case_name}.txt"
    
    #print(f"Running case: {case_name}")
    
    # 1. 解答プログラムを実行
    try:
        subprocess.run(
            [str(EXE_PATH), str(input_file), str(output_file)], 
            check=True, capture_output=True, text=True, timeout=10
        )
    except subprocess.CalledProcessError as e:
        print(f"  -> ERROR: Solver program failed for case {case_name}.")
        print(e.stderr)
        continue
    except subprocess.TimeoutExpired as e:
        print(f"  -> ERROR: Solver program timed out for case {case_name}.")
        continue

    # 2. スコア計算プログラムを実行
    try:
        result = subprocess.run(
            [str(SCORER_PATH), str(input_file), str(output_file)], 
            check=True, capture_output=True, text=True, timeout=10
        )
    except subprocess.CalledProcessError as e:
        print(f"  -> ERROR: Scorer program failed for case {case_name}.")
        print(e.stderr)
        continue
    except subprocess.TimeoutExpired as e:
        print(f"  -> ERROR: Scorer program timed out for case {case_name}.")
        continue
    
    # 3. スコアを抽出
    score_found = False
    output_text = result.stdout + result.stderr
    for line in output_text.splitlines():
        if "Score =" in line:
            try:
                score_str = line.split("=")[1].strip()
                score = int(score_str)
                #print(f"  -> Score: {score}")
                print(score)
                total_score += score
                score_found = True
                break
            except (ValueError, IndexError):
                # スコアのパースに失敗
                pass
    
    if not score_found:
        print(f"  -> Score: ERROR (Could not parse score from output)")
        print(output_text)
        
print("--------------------")
#print(f"Total Score: {total_score}")
print(total_score)


これで各テストケースのスコアと合計得点がすぐ分かるようになりました。
自動実行のプログラムで点数計算しても良かったのですが、マラソン系コンテストでは点数計算用の実行ファイルが渡されることがあるようなので、その形式に則ってみました。

 2-3. ビジュアライザースコアから交点が解消されているかは分かるのですが、実際に見てみないと実感がわきませんよね！

見える化することで次にどのようなアプローチをすべきかも見えてくるかもしれません。
なのでビジュアライザーを作ります。
こちらはPythonのmatplotlibで作成しました。
import sys
from pathlib import Path
import math
import matplotlib.pyplot as plt
from matplotlib.widgets import Button

def dist(p1, p2):
    """2点間のユークリッド距離を計算する"""
    return math.sqrt((p1[0] - p2[0])**2 + (p1[1] - p2[1])**2)

def cross_product(p1, p2, p3):
    """3つの点の外積を計算する"""
    return (p2[0] - p1[0]) * (p3[1] - p1[1]) - (p2[1] - p1[1]) * (p3[0] - p1[0])

def is_on_segment(p1, p2, p):
    """点が線分上にあるか判定する"""
    return (min(p1[0], p2[0]) <= p[0] <= max(p1[0], p2[0]) and
            min(p1[1], p2[1]) <= p[1] <= max(p1[1], p2[1]))

def has_intersection(p1, p2, p3, p4):
    """2つの線分が真に交差するか判定する（端点や線上での接触は除く）"""
    cp1 = cross_product(p1, p2, p3)
    cp2 = cross_product(p1, p2, p4)
    cp3 = cross_product(p3, p4, p1)
    cp4 = cross_product(p3, p4, p2)

    # 真の交差（両方の線分が互いをまたぐ）の場合のみTrueを返す
    return ((cp1 > 0 and cp2 < 0) or (cp1 < 0 and cp2 > 0)) and \
           ((cp3 > 0 and cp4 < 0) or (cp3 < 0 and cp4 > 0))

def calculate_metrics(points, path):
    """紐の長さと交点の数を計算する"""
    total_length = 0
    for i in range(len(path) - 1):
        total_length += dist(points[path[i]-1], points[path[i+1]-1])

    crossings = 0
    segments = []
    for i in range(len(path) - 1):
        segments.append((points[path[i]-1], points[path[i+1]-1]))

    for i in range(len(segments)):
        for j in range(i + 1, len(segments)):
            # 隣接する線分はチェックしない
            if abs(i - j) > 1:
                 if has_intersection(segments[i][0], segments[i][1], segments[j][0], segments[j][1]):
                    crossings += 1
    
    return total_length, crossings

def read_input_file(filepath):
    """入力ファイルを読み込み、初期の点とパスを返す"""
    with open(filepath, 'r') as f:
        lines = f.readlines()
    n, _ = map(int, lines[0].split())
    points = [tuple(map(int, line.split())) for line in lines[1:n+1]]
    path = list(range(1, n + 1))
    return points, path

def read_output_file(filepath, initial_points):
    """出力ファイルを読み込み、最終的な点とパスを返す"""
    with open(filepath, 'r') as f:
        lines = f.readlines()
    m = int(lines[0])
    final_points = list(initial_points)
    added_indices = []
    if m > 0:
        for i in range(m):
            x, y = map(int, lines[i + 1].split())
            final_points.append((x, y))
            added_indices.append(len(initial_points) + i)
    path = [int(line.strip()) for line in lines[m + 1:] if line.strip()]
    return final_points, path, added_indices

def draw_graph(ax, title, points, path, added_indices=None):
    """指定されたサブプロットにグラフを描画する"""
    ax.cla() # 描画内容をクリア

    # メトリクスを計算
    length, crossings = calculate_metrics(points, path)
    
    # タイトルを設定
    full_title = f"{title}\nLength: {length:.2f}, Crossings: {crossings}"
    ax.set_title(full_title)
    
    ax.set_aspect('equal', adjustable='box')
    ax.grid(True, linestyle='--', alpha=0.6)

    # パスを描画
    path_x = [points[p - 1][0] for p in path]
    path_y = [points[p - 1][1] for p in path]
    ax.plot(path_x, path_y, 'o-', color='lightblue', markersize=4, zorder=1, label='Path')

    # 点を描画
    initial_points_x = [p[0] for i, p in enumerate(points) if added_indices is None or i not in added_indices]
    initial_points_y = [p[1] for i, p in enumerate(points) if added_indices is None or i not in added_indices]
    ax.scatter(initial_points_x, initial_points_y, color='blue', zorder=2, label='Initial Nails')

    # 追加された点があれば描画
    if added_indices:
        added_points_x = [points[i][0] for i in added_indices]
        added_points_y = [points[i][1] for i in added_indices]
        ax.scatter(added_points_x, added_points_y, color='red', zorder=2, marker='s', label='Added Nails')
    
    ax.legend()

class Visualizer:
    def __init__(self):
        self.test_cases = sorted(Path("tools/in").glob("*.txt"))
        if not self.test_cases:
            print("[ERROR] No test cases found in 'tools/in' directory.")
            sys.exit(1)
        
        self.current_index = 0
        self.fig, (self.ax1, self.ax2) = plt.subplots(1, 2, figsize=(14, 7))
        plt.subplots_adjust(bottom=0.2)

        self._setup_widgets()
        self.update_plot()

    def _setup_widgets(self):
        ax_prev = plt.axes([0.7, 0.05, 0.1, 0.075])
        ax_next = plt.axes([0.81, 0.05, 0.1, 0.075])
        self.btn_prev = Button(ax_prev, 'Prev')
        self.btn_next = Button(ax_next, 'Next')
        self.btn_prev.on_clicked(self.prev_case)
        self.btn_next.on_clicked(self.next_case)

    def update_plot(self):
        input_file = self.test_cases[self.current_index]
        case_number = input_file.stem
        output_file = Path(f"tools/out/{case_number}.txt")

        if not output_file.exists():
            print(f"[INFO] Output for {case_number} not found, skipping final state.")
            initial_points, initial_path = read_input_file(input_file)
            draw_graph(self.ax1, f"Initial State ({case_number}.txt)", initial_points, initial_path)
            self.ax2.cla()
            self.ax2.set_title(f"Final State ({case_number}.txt) - Not Found")
            self.ax2.text(0.5, 0.5, 'Run `test.py` to generate output.', ha='center', va='center')
            self.fig.canvas.draw_idle()
            return

        initial_points, initial_path = read_input_file(input_file)
        final_points, final_path, added_indices = read_output_file(output_file, initial_points)

        # 表示範囲を動的に計算
        all_x = [p[0] for p in final_points]
        all_y = [p[1] for p in final_points]
        x_min, x_max = min(all_x), max(all_x)
        y_min, y_max = min(all_y), max(all_y)
        x_margin = (x_max - x_min) * 0.1 if (x_max - x_min) > 0 else 10
        y_margin = (y_max - y_min) * 0.1 if (y_max - y_min) > 0 else 10

        # 描画
        draw_graph(self.ax1, f"Initial State ({case_number}.txt)", initial_points, initial_path)
        draw_graph(self.ax2, f"Final State ({case_number}.txt)", final_points, final_path, added_indices)

        # 両方のグラフの表示範囲を揃える
        self.ax1.set_xlim(x_min - x_margin, x_max + x_margin)
        self.ax1.set_ylim(y_min - y_margin, y_max + y_margin)
        self.ax2.set_xlim(x_min - x_margin, x_max + x_margin)
        self.ax2.set_ylim(y_min - y_margin, y_max + y_margin)

        self.fig.canvas.draw_idle()

    def next_case(self, event):
        self.current_index = (self.current_index + 1) % len(self.test_cases)
        self.update_plot()

    def prev_case(self, event):
        self.current_index = (self.current_index - 1 + len(self.test_cases)) % len(self.test_cases)
        self.update_plot()

if __name__ == "__main__":
    app = Visualizer()
    plt.show()


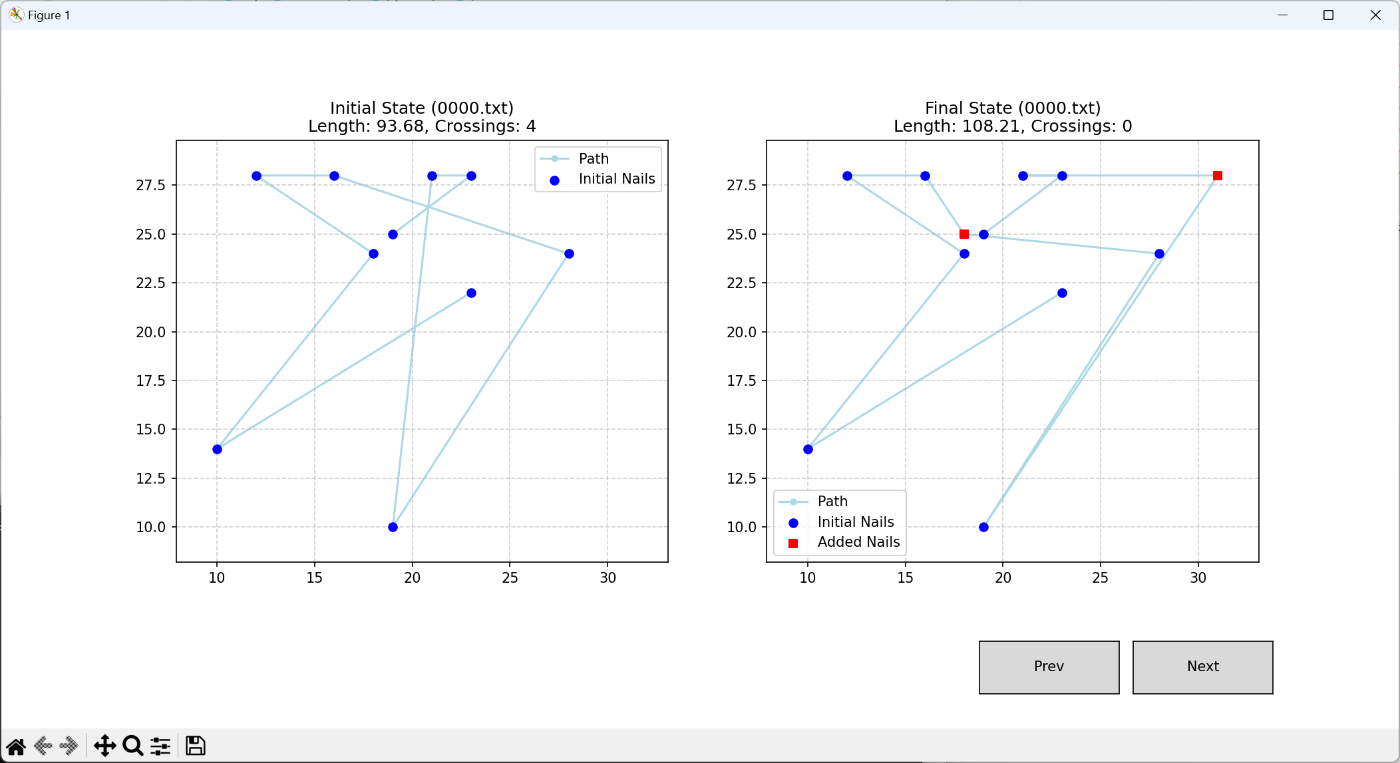
いいですね。

釘を打つ前後でどのように変わったのかが一目瞭然です。
PrevとNextを押すことで別のテストケースを見ることもできます。

 2-4. 実際に使ってみたではスコアはどちらの方が良かったのでしょうか？

全探索の手法1(5秒で打ち切り)、見つけたら修正する手法2のスコアを比較してみます。
今回のテストケースは以下の通り作成しました。

N=2~20を10ケース

N=20~100を10ケース

N=100~500を10ケース

N=500~1000を5ケース
手法1(全探索)：119,022

手法2(見つけたら修正)：72,559
全探索の方がスコアが高かったですね。
ビジュアライザーで見てみると、



点が少なめの時はちゃんと改善できてますね。

点が多くなると何もできなくなっているみたいです…

手法1,2どちらも同じような結果になりました。

 2-5. 単体テスト今回言語をC#に選んだのは実行環境があるというのもありますし、単体テストが作れるというのもありました。

プログラミング中、このケースってどうなんだ？みたいに不安になるときがあるので、それを明文化できるのは良いですよね。
なので作成したユーティリティ関数などは単体テストを作成しました。
[TestMethod]
[TestCategory("SegIntersectStrict")] // テストをグループ化するためのカテゴリ属性
public void 単純に交差する線分はTrueを返す()
{
	// Arrange: X字状に交差する線分を用意
	var a = new P(0, 0);
	var b = new P(5, 5);
	var c = new P(0, 5);
	var d = new P(5, 0);

	// Act: 交差判定を実行
	bool result = SegIntersectStrict(a, b, c, d);

	// Assert: 結果がTrueであることを確認
	Assert.IsTrue(result, "線分は交差するはずです。");
}

[TestMethod]
[TestCategory("SegIntersectStrict")]
public void 平行で交差しない線分はFalseを返す()
{
	// Arrange: 平行な線分を用意
	var a = new P(0, 0);
	var b = new P(5, 5);
	var c = new P(1, 0);
	var d = new P(6, 5);

	// Act: 交差判定を実行
	bool result = SegIntersectStrict(a, b, c, d);

	// Assert: 結果がFalseであることを確認
	Assert.IsFalse(result, "平行線は交差しないはずです。");
}

[TestMethod]
[TestCategory("SegIntersectStrict")]
public void 端点で接する線分はFalseを返す()
{
	// Arrange: 端点のみを共有する線分を用意
	var a = new P(0, 0);
	var b = new P(5, 5);
	var c = new P(5, 5);
	var d = new P(10, 10);

	// Act: 交差判定を実行
	bool result = SegIntersectStrict(a, b, c, d);

	// Assert: 結果がFalseであることを確認
	Assert.IsFalse(result, "厳密な交差判定(Strict)では、端点での接触は交差とみなされません。");
}
// ...

 3. 端点探索2
 3-1. 計算量削減1_周辺探索削減ではコンテストのプログラム改善に移ります。
ここで周辺探索の計算量が多いのではないか？という疑問が湧きました。

なので試しに周辺探索を必要最小限にしてみました。
// 候補生成1: 端点+周辺探索
public static void FindCandidatesByEndpoint(List<P> allPts, List<int> path, double intersectionX, double intersectionY, List<Cand> candidates, int segPos, int endpointIndex)
{
	const int Dmax = 5;
	const int searchRadius = 0;

	P pOld = allPts[endpointIndex];
	int dxSign = SgnLl((long)Math.Round(pOld.X - intersectionX));
	int dySign = SgnLl((long)Math.Round(pOld.Y - intersectionY));
	if (dxSign == 0 && dySign == 0) { dxSign = 1; dySign = 1; }

	for (int d = 1; d <= Dmax; d += 2)
	{
		P centerP = new P(pOld.X + dxSign * d, pOld.Y + dySign * d);
		for (int dx = -searchRadius; dx <= searchRadius; ++dx)
		{
			for (int dy = -searchRadius; dy <= searchRadius; ++dy)
			{
				AddCandidateIfValid(allPts, path, candidates, segPos, new P(centerP.X + dx, centerP.Y + dy));
			}
		}
	}
}
周辺探索の3重for文の計算量が非常に多そうですよね。

端点の延長線上の1,3,5を探索するだけにしました。
スコアは以下の通りです。

手法1(全探索)：353,634

手法2(見つけたら修正)：33,012
手法2は下がりましたが、手法1の方が3倍に上がりましたね。

 3-2. 探索交点削減今まではすべての交点に対して端点探索を行っていました。

そこで、交点をサンプリングして改善していくという手法を取ってみます。
全ての交点の中からランダムで10個取得して、改善していくという感じですね。
while (usedK < K)
{
	if (TotalCrossings(allPts, path) == 0) break;

	var candidates = new List<Cand>();
	int L = path.Count;

	// 存在する全ての交差ペアをリストアップする
	var allCrossingPairs = new List<(int i, int j)>();
	for (int i = 0; i < L - 1; ++i)
	{
		for (int j = i + 2; j < L - 1; ++j)
		{
			int ai = path[i], aj = path[i + 1], bi = path[j], bj = path[j + 1];
			if (SegIntersectStrict(allPts[ai - 1], allPts[aj - 1], allPts[bi - 1], allPts[bj - 1]))
			{
				allCrossingPairs.Add((i, j));
			}
		}
	}

	int sampleSize = Math.Min(allCrossingPairs.Count, 10);
	var sampledPairs = allCrossingPairs.OrderBy(x => random.Next()).Take(sampleSize);

	// サンプリングされたペアについてのみ、候補手を生成・評価する
	foreach (var pair in sampledPairs)
	{
		int i = pair.i;
		int j = pair.j;
		int ai = path[i], aj = path[i + 1], bi = path[j], bj = path[j + 1];

		var ip = IntersectionPoint(allPts[ai - 1], allPts[aj - 1], allPts[bi - 1], allPts[bj - 1]);

		FindCandidatesByEndpoint(allPts, path, ip.x, ip.y, candidates, i, bi - 1);
		FindCandidatesByEndpoint(allPts, path, ip.x, ip.y, candidates, i, bj - 1);
		FindCandidatesByEndpoint(allPts, path, ip.x, ip.y, candidates, j, ai - 1);
		FindCandidatesByEndpoint(allPts, path, ip.x, ip.y, candidates, j, aj - 1);
	}

	// 貪欲法
}
スコア：4,437,119

スコアが桁違いに上がりました。
続いてビジュアライザーを見てみましょう。





テストケース6の交点が増えています。周辺探索を減らしたからでしょうか？
大切なのはテストケース26です、釘の打つ量が段違いになりました。

これおかげで交点が3000ほど減っています。単純スコアにして3000×50=150,000点です。
ここら辺で全文を一旦公開します。
using System;
using System.Collections.Generic;
using System.IO;
using System.Linq;
using System.Globalization;

public class Program
{
    // 点の座標
    public struct P
    {
        public int X, Y;
        public P(int x, int y) { X = x; Y = y; }
    }

    // 改善候補の手を格納するクラス
    public class Cand : IComparable<Cand>
    {
        public int InsertPos;     // path のどの位置の後ろに挿入するか
        public P Coord;           // 新しい釘の座標
        public int Reduce;        // この手を打った時の交差減少数
        public double DeltaLen;   // この手を打った時の紐の増加長

        public int CompareTo(Cand other)
        {
            double myImprovement = (this.Reduce * 50.0) - this.DeltaLen;
            double otherImprovement = (other.Reduce * 50.0) - other.DeltaLen;

            // スコア改善量が大きい方を優先
            if (Math.Abs(myImprovement - otherImprovement) > 1e-9)
            {
                return otherImprovement.CompareTo(myImprovement); // 降順
            }
            // ... (改善量が同じなら、既存のルールでOK)
            if (Coord.X != other.Coord.X) return Coord.X.CompareTo(other.Coord.X);
            return Coord.Y.CompareTo(other.Coord.Y);
        }
    }

    private static Random random = new Random(0);

    public static void Main(string[] args)
    {
        // コマンドライン引数から入出力ファイルを指定
        if (args.Length < 2)
        {
            // 引数がない場合は標準入出力で実行
            Solve();
            return;
        }

        string inputFile = args[0];
        string outputFile = args[1];

        // ファイル入出力に切り替え
        using (var reader = new StreamReader(inputFile))
        using (var writer = new StreamWriter(outputFile))
        {
            Console.SetIn(reader);
            Console.SetOut(writer);
            Solve();
        }
    }

    public static void Solve()
    {
        var stopwatch = System.Diagnostics.Stopwatch.StartNew();
        const double TimeLimitMs = 4900;

        // 高速入出力のための準備
        var culture = CultureInfo.InvariantCulture;

        string line = Console.ReadLine();
        if (string.IsNullOrEmpty(line)) return;

        string[] parts = line.Split();
        int N = int.Parse(parts[0]);
        int K = int.Parse(parts[1]);

        var basePts = new List<P>(N);
        for (int i = 0; i < N; i++)
        {
            parts = Console.ReadLine().Split();
            basePts.Add(new P(int.Parse(parts[0]), int.Parse(parts[1])));
        }

        var path = Enumerable.Range(1, N).ToList();
        var allPts = new List<P>(basePts);

        int usedK = 0;

        while (usedK < K)
        {
	        if (stopwatch.Elapsed.TotalMilliseconds > TimeLimitMs)
			{
				break; // 時間切れなら強制終了
			}
            
            if (TotalCrossings(allPts, path) == 0) break;

            var candidates = new List<Cand>();
            int L = path.Count;

            // 1. まず、存在する全ての交差ペアをリストアップする
            var allCrossingPairs = new List<(int i, int j)>();
            for (int i = 0; i < L - 1; ++i)
            {
                for (int j = i + 2; j < L - 1; ++j)
                {
                    int ai = path[i], aj = path[i + 1], bi = path[j], bj = path[j + 1];
                    if (SegIntersectStrict(allPts[ai - 1], allPts[aj - 1], allPts[bi - 1], allPts[bj - 1]))
                    {
                        allCrossingPairs.Add((i, j));
                    }
                }
            }

            int sampleSize = Math.Min(allCrossingPairs.Count, 10);
            var sampledPairs = allCrossingPairs.OrderBy(x => random.Next()).Take(sampleSize);

            // 3. サンプリングされたペアについてのみ、候補手を生成・評価する
            foreach (var pair in sampledPairs)
            {
                int i = pair.i;
                int j = pair.j;
                int ai = path[i], aj = path[i + 1], bi = path[j], bj = path[j + 1];

                var ip = IntersectionPoint(allPts[ai - 1], allPts[aj - 1], allPts[bi - 1], allPts[bj - 1]);

                // --- 候補生成 ---
                FindCandidatesByEndpoint(allPts, path, ip.x, ip.y, candidates, i, bi - 1);
                FindCandidatesByEndpoint(allPts, path, ip.x, ip.y, candidates, i, bj - 1);
                FindCandidatesByEndpoint(allPts, path, ip.x, ip.y, candidates, j, ai - 1);
                FindCandidatesByEndpoint(allPts, path, ip.x, ip.y, candidates, j, aj - 1);
            }

            if (candidates.Count == 0) continue;

            // 1. 今回の「最善手」を見つける (比較のため)
            candidates.Sort();
            Cand bestCand = candidates[0];

            // 最終的に選ばれた手を適用
            allPts.Add(bestCand.Coord);
            path.Insert(bestCand.InsertPos + 1, allPts.Count);
            usedK++;
        }

        int M = allPts.Count - N;
        Console.WriteLine(M);
        for (int i = 0; i < M; i++)
        {
            Console.WriteLine($"{allPts[N + i].X} {allPts[N + i].Y}");
        }
        foreach (int v in path)
        {
            Console.WriteLine(v);
        }
    }

    // --- 候補生成ヘルパー関数 ---
    public static void AddCandidateIfValid(List<P> allPts, List<int> path, List<Cand> candidates, int segPos, P candP)
    {
        if (candP.X < 0 || candP.X > 1000 || candP.Y < 0 || candP.Y > 1000) return;

        foreach (var p in allPts) if (p.X == candP.X && p.Y == candP.Y) return;

        int reduce = CalculateCrossingDelta(allPts, path, segPos, candP);
        if (reduce <= 0) return;

        P P1 = allPts[path[segPos] - 1];
        P P2 = allPts[path[segPos + 1] - 1];
        double deltaLen = Dist(P1, candP) + Dist(candP, P2) - Dist(P1, P2);

        candidates.Add(new Cand
        {
            InsertPos = segPos,
            Coord = candP,
            Reduce = reduce,
            DeltaLen = deltaLen
        });
    }

    // 候補生成1: 端点+周辺探索
    public static void FindCandidatesByEndpoint(List<P> allPts, List<int> path, double intersectionX, double intersectionY, List<Cand> candidates, int segPos, int endpointIndex)
    {
        const int Dmax = 5;
        const int searchRadius = 0;

        P pOld = allPts[endpointIndex];
        int dxSign = SgnLl((long)Math.Round(pOld.X - intersectionX));
        int dySign = SgnLl((long)Math.Round(pOld.Y - intersectionY));
        if (dxSign == 0 && dySign == 0) { dxSign = 1; dySign = 1; }

        for (int d = 1; d <= Dmax; d += 2)
        {
            P centerP = new P(pOld.X + dxSign * d, pOld.Y + dySign * d);
            for (int dx = -searchRadius; dx <= searchRadius; ++dx)
            {
                for (int dy = -searchRadius; dy <= searchRadius; ++dy)
                {
                    AddCandidateIfValid(allPts, path, candidates, segPos, new P(centerP.X + dx, centerP.Y + dy));
                }
            }
        }
    }

    // --- ユーティリティ関数 ---
    public static long CrossLl(long x1, long y1, long x2, long y2) => x1 * y2 - y1 * x2;
    public static long Cross(P a, P b, P c) => CrossLl(b.X - a.X, b.Y - a.Y, c.X - a.X, c.Y - a.Y);
    public static int SgnLl(long v) => v > 0 ? 1 : (v < 0 ? -1 : 0);

    public static bool SegIntersectStrict(P a, P b, P c, P d)
    {
        if (Math.Max(a.X, b.X) < Math.Min(c.X, d.X) || Math.Max(c.X, d.X) < Math.Min(a.X, b.X) ||
            Math.Max(a.Y, b.Y) < Math.Min(c.Y, d.Y) || Math.Max(c.Y, d.Y) < Math.Min(a.Y, b.Y))
        {
            return false;
        }
        long c1 = Cross(a, b, c), c2 = Cross(a, b, d), c3 = Cross(c, d, a), c4 = Cross(c, d, b);
        return (c1 > 0 && c2 < 0 || c1 < 0 && c2 > 0) && (c3 > 0 && c4 < 0 || c3 < 0 && c4 > 0);
    }

    public static (double x, double y) IntersectionPoint(P a, P b, P c, P d)
    {
        double A1 = b.Y - a.Y, B1 = a.X - b.X, C1 = A1 * a.X + B1 * a.Y;
        double A2 = d.Y - c.Y, B2 = c.X - d.X, C2 = A2 * c.X + B2 * c.Y;
        double det = A1 * B2 - A2 * B1;
        double x = (B2 * C1 - B1 * C2) / det;
        double y = (A1 * C2 - A2 * C1) / det;
        return (x, y);
    }

    public static double Dist(P a, P b)
    {
        double dx = a.X - b.X, dy = a.Y - b.Y;
        return Math.Sqrt(dx * dx + dy * dy);
    }

    public static int TotalCrossings(List<P> pts, List<int> path)
    {
        int L = path.Count;
        int cnt = 0;
        for (int i = 0; i < L - 1; i++)
        {
            for (int j = i + 2; j < L - 1; j++)
            {
                int ai = path[i], aj = path[i + 1], bi = path[j], bj = path[j + 1];
                if (SegIntersectStrict(pts[ai - 1], pts[aj - 1], pts[bi - 1], pts[bj - 1])) cnt++;
            }
        }
        return cnt;
    }

    public static int CalculateCrossingDelta(List<P> pts, List<int> path, int segPosToChange, P newNailS)
    {
        int L = path.Count;
        if (segPosToChange < 0 || segPosToChange + 1 >= L) return 0;

        int p1Idx = path[segPosToChange];
        int p2Idx = path[segPosToChange + 1];
        P P1 = pts[p1Idx - 1];
        P P2 = pts[p2Idx - 1];

        int removed = 0, added = 0;

        for (int i = 0; i < L - 1; ++i)
        {
            if (i == segPosToChange) continue;

            int op1Idx = path[i];
            int op2Idx = path[i + 1];
            P OP1 = pts[op1Idx - 1];
            P OP2 = pts[op2Idx - 1];

            if (SegIntersectStrict(P1, P2, OP1, OP2)) removed++;
            if (SegIntersectStrict(P1, newNailS, OP1, OP2)) added++;
            if (SegIntersectStrict(newNailS, P2, OP1, OP2)) added++;
        }
        return removed - added;
    }
}

 4. 焼きなまし法続いて、貪欲法から焼きなまし法にアップグレードします。
// ★★★ 焼きなまし法のパラメータ設定 ★★★
double startTemp = 100.0; // 開始温度 (スコア改善量のスケールに合わせる)
double endTemp = 0.1;   // 終了温度

while (usedK < K)
{
	// 交点探索

	foreach (var pair in sampledPairs)
	{
		// 端点探索
	}

	if (candidates.Count == 0) break;

	// ★★★ ここからが焼きなまし法の中核 ★★★

	// 1. 今回の「最善手」を見つける (比較のため)
	candidates.Sort();
	Cand bestCand = candidates[0];
	double bestImprovement = (bestCand.Reduce * 50.0) - bestCand.DeltaLen;

	// 2. 採用する手を「確率的」に選ぶ
	//    候補の中からランダムに一つ選ぶ (多様性を確保)
	Cand chosenCand = candidates[random.Next(candidates.Count)];
	double chosenImprovement = (chosenCand.Reduce * 50.0) - chosenCand.DeltaLen;

	// 3. 温度を計算 (線形に減少させる)
	double progress = (double)usedK / K;
	double currentTemp = startTemp * (1.0 - progress) + endTemp * progress;

	// 4. 手を採択するかどうかの決定 (メトロポリス法)
	Cand finalCand;
	// 常に「より良い手」は受け入れる
	if (chosenImprovement > bestImprovement)
	{
		finalCand = chosenCand;
	}
	else
	{
		// 「悪い手」をどのくらいの確率で受け入れるか計算
		double diff = bestImprovement - chosenImprovement;
		double probability = Math.Exp(-diff / currentTemp);

		if (random.NextDouble() < probability)
		{
			// 悪い手(chosenCand)をあえて採用する
			finalCand = chosenCand;
		}
		else
		{
			// やはり最善手(bestCand)を採用する
			finalCand = bestCand;
		}
	}
	// ★★★ 焼きなまし法のロジックここまで ★★★

	// 最終的に選ばれた手を適用
	allPts.Add(finalCand.Coord);
	path.Insert(finalCand.InsertPos + 1, allPts.Count);
	usedK++;
}
スコア：4,437,119→4,465,150

スコアはそこまで上がりませんでしたね。
あ、AddCandidateIfValidの評価もゆるくする必要がありますね。

交点改善が0なら採用しないという方針なので、スコアが20点までなら下がってもいいくらいにすると良いかもしれませんね。
最善手以外の手法も取り入れるのは場合によっては良いかもしれません。

パラメータ調整で結果が変わるのも嬉しいですよね。

 5. 上手くいったこと
 5-1. 計算量削減2_線分グリッド管理前項目で計算量を削減することでスコアが上がることがわかりました。

なのでネックとなっている処理を改善していくことでスコアが上がるかもしれません。
次の改善は、線分の存在管理をグリッド状ごとに行います。

こうすることで、交点の探索を行うときに必要最低限の線分に限定できます。
スコア：4,437,119→4,520,962

 5-2. 処理高速化座標管理をHashSetにすることで座標チェックが早くなりました。
交点チェックで、変数を定義する回数を減らしました。
for (int i = 0; i < L - 1; ++i)
{
	int ai = path[i], aj = path[i + 1];
	P p_ai = allPts[ai - 1];
	P p_aj = allPts[aj - 1];

	for (int j = i + 2; j < L - 1; ++j)
	{
		int bi = path[j], bj = path[j + 1];
		if (SegIntersectStrict(p_ai, p_aj, allPts[bi - 1], allPts[bj - 1]))
		{
			allCrossingPairs.Add((i, j));
		}
	}
}
スコア：4,520,962→4,539,594

 5-3. 中点法線探索今までは端点の周りから選んでいましたが、他のアルゴリズムも採用してみます。

提案された方法として、中点法線探索が挙げられました。
交点から各線分の垂直方向に伸ばして、そこから採用するアイディアみたいです。
端点探索だけでは探索できない箇所も探索するようですね。

たしかに、線分同士が平行に近い(角度が浅い)時は全然違う点が候補になりそうですね。
public static void AddMidpointNormalCandidates(List<P> allPts, List<int> path, List<Cand> candidates, int segPosToInsert, int crossingSegIndex, HashSet<P> existingCoords)
{
	// 迂回させたい線分 (この線分の間に釘が挿入される)
	P P1 = allPts[path[segPosToInsert] - 1];
	P P2 = allPts[path[segPosToInsert + 1] - 1];

	// 障害物となる線分 (この線分から離れるようにする)
	P OP1 = allPts[path[crossingSegIndex] - 1];
	//P OP2 = allPts[path[crossingSegIndex + 1] - 1]; // 障害物側の点は片方あれば十分

	// 1. 迂回したい線分の中点を計算
	double midX = (P1.X + P2.X) / 2.0;
	double midY = (P1.Y + P2.Y) / 2.0;

	// 2. 線分の方向ベクトルから、それに垂直な法線ベクトルを計算
	double vecX = P2.X - P1.X;
	double vecY = P2.Y - P1.Y;

	double normX = -vecY;
	double normY = vecX;

	// 3. 2つある法線方向のうち、どちらが障害物から離れる方向かを判定
	//    中点Mから障害物の点OP1へのベクトルと、法線ベクトルの内積を見る
	double dot = (OP1.X - midX) * normX + (OP1.Y - midY) * normY;

	// 4. 法線ベクトルを正規化(長さを1に)して、移動方向の単位ベクトルを求める
	double normLen = Math.Sqrt(normX * normX + normY * normY);
	if (normLen < 1e-9) return; // 線分が点になっているなど、異常なケースを避ける

	double moveDx = normX / normLen;
	double moveDy = normY / normLen;

	// もし内積が正なら、法線は障害物と同じ方向を向いているので、逆方向にする
	if (dot > 0)
	{
		moveDx = -moveDx;
		moveDy = -moveDy;
	}

	// 5. 中点から、計算した方向に一定距離進んだ点を候補として生成
	for (int d = 5; d <= 15; d += 5) // 試す距離を調整
	{
		P candP = new P((int)Math.Round(midX + moveDx * d), (int)Math.Round(midY + moveDy * d));

		// 既存のAddCandidateIfValidヘルパーを使って、候補の有効性チェックと追加を行う
		AddCandidateIfValid(allPts, path, candidates, segPosToInsert, candP, existingCoords);
	}
}
スコア：4,539,594→4,437,515

スコアが下がってますね、計算量が増えたからでしょうか。
ですがテストケースを眺めていると、交点の少ないケースでは点数が上がっていることがわかりました。

なので、交点が700以下だったら実行するようにしましょう。
スコア：4,539,594→4,544,402

微妙に上がりました。

本番のテストケースに、Nが少ないケースが多い可能性も考えてあってもいいかもしれませんね。

 5-4. 全て釘を打ち終わった後に周辺探索釘を打ち終わった後に実行時間に余裕がありそうだったら、釘を周辺に動かしてみます。

運が良ければ交点が減るかもしれませんし、長さが減るかもしれません。
元々実行時間削減のために周辺探索を打ち切っていたので、実行時間に余裕がある時に復活させます。
while (stopwatch.Elapsed.TotalMilliseconds < TimeLimitMs)
{
	int addedNailCount = allPts.Count - N;
	if (addedNailCount == 0) break; // 動かせる釘がない

	double bestMoveImprovement = -1.0;
	int bestNailToMove = -1;
	P bestNewCoord = new P(-1, -1);

	// 追加した釘の中から、ランダムにいくつかを選んで評価する
	const int moveCandidateCount = 10;
	for (int i = 0; i < moveCandidateCount; ++i)
	{
		if (stopwatch.Elapsed.TotalMilliseconds > TimeLimitMs) break;

		int nailIndexToMove = N + random.Next(addedNailCount);
		P currentCoord = allPts[nailIndexToMove];

		// 周辺1マスだけを素早く探索
		for (int dx = -1; dx <= 1; ++dx)
		{
			for (int dy = -1; dy <= 1; ++dy)
			{
				if (dx == 0 && dy == 0) continue;

				P newCoord = new P(currentCoord.X + dx, currentCoord.Y + dy);

				// --- 座標の有効性チェック ---
				if (newCoord.X < 0 || newCoord.X > 1000 || newCoord.Y < 0 || newCoord.Y > 1000) continue;

				// ★★★【重要】既存の釘との重複チェック ★★★
				bool exists = false;
				for (int ptIndex = 0; ptIndex < allPts.Count; ++ptIndex)
				{
					// 自分自身の移動前の位置はチェック対象外
					if (ptIndex == nailIndexToMove) continue;

					if (allPts[ptIndex].X == newCoord.X && allPts[ptIndex].Y == newCoord.Y)
					{
						exists = true;
						break;
					}
				}
				if (exists) continue; // 他の釘と重複するなら、この移動先は無効

				// --- 評価 ---
				double improvement = CalculateMoveImprovement(allPts, path, nailIndexToMove, newCoord);

				if (improvement > bestMoveImprovement)
				{
					bestMoveImprovement = improvement;
					bestNailToMove = nailIndexToMove;
					bestNewCoord = newCoord;
				}
			}
		}
	}

	if (bestMoveImprovement > 0)
	{
		allPts[bestNailToMove] = bestNewCoord;
	}
	else
	{
		break; // 改善が見込めないので終了
	}
}
public static double CalculateMoveImprovement(List<P> allPts, List<int> path, int nailIndexToMove, P newCoord)
{
	int nailId = nailIndexToMove + 1;
	int pathIndexOfNail = -1;
	for (int i = 0; i < path.Count; ++i) { if (path[i] == nailId) { pathIndexOfNail = i; break; } }

	if (pathIndexOfNail <= 0 || pathIndexOfNail >= path.Count - 1) return -1.0;

	P pOld = allPts[nailIndexToMove];
	P pPrev = allPts[path[pathIndexOfNail - 1] - 1];
	P pNext = allPts[path[pathIndexOfNail + 1] - 1];

	double oldLen = Dist(pPrev, pOld) + Dist(pOld, pNext);
	double newLen = Dist(pPrev, newCoord) + Dist(newCoord, pNext);
	double lenImprovement = oldLen - newLen;

	int removed = 0, added = 0;
	for (int i = 0; i < path.Count - 1; ++i)
	{
		if (i == pathIndexOfNail || i == pathIndexOfNail - 1) continue;

		P op1 = allPts[path[i] - 1];
		P op2 = allPts[path[i + 1] - 1];

		if (SegIntersectStrict(pPrev, pOld, op1, op2)) removed++;
		if (SegIntersectStrict(pOld, pNext, op1, op2)) removed++;
		if (SegIntersectStrict(pPrev, newCoord, op1, op2)) added++;
		if (SegIntersectStrict(newCoord, pNext, op1, op2)) added++;
	}
	int crossImprovement = removed - added;

	return (crossImprovement * 50.0) + lenImprovement;
}
スコア：4,544,402→4,600,877

たかが周辺1マスしか探索してないのに結構変わりますね。

 5-5. 計算量削減3_パフォーマンスプロファイラー具体的にどの行でパフォーマンスが落ちているのか、プログラムだけでは分からないこともあります。

Visual Studioの機能でCPU使用率がどこでボトルネックになっているのか可視化する、パフォーマンスプロファイラーという機能があります。

それを使ってみました。


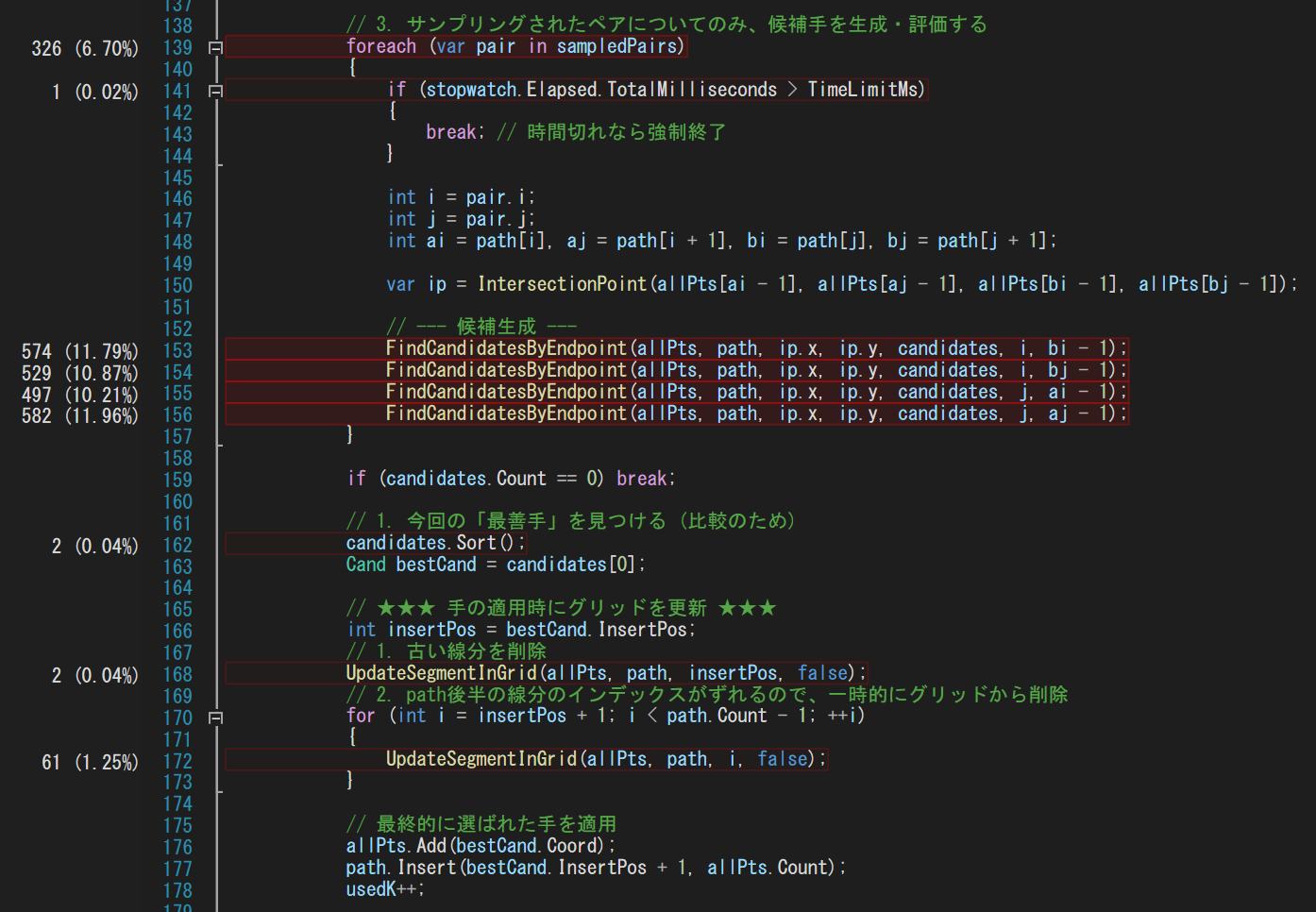
気になったのは上記の2つです。

1枚目は変数定義とList追加に負荷が多いですね。

変数定義は5-2で改善した内容でしたね。
2枚目は端点探索に40%使っているのは仕方ないとして、foreachに6%使っていますね。

これはLinqを組んでいるためこのようになったのでしょう。
なので改善していきます。
List追加に関しては、配列に代入なら早くなるでしょう。

多めの配列に格納していったあと、必要最低限の配列にコピーという流れにします。
// ★★★ 1. 巨大な固定長配列を一度だけ確保 ★★★
// 交差ペアの最大数は N*(N-1)/2 程度だが、そこまでいくことは稀。
// N=1000なら約50万。余裕をもって設定。
const int MaxPairs = 500000;
var crossingPairsBuffer = new (int i, int j)[MaxPairs];

while (usedK < K)
{
	int L = path.Count;

	// 1. まず、存在する全ての交差ペアをリストアップする
	// ★★★ 2. List.Add()の代わりに、配列に直接書き込む ★★★
	int pairCount = 0;

	for (int i = 0; i < L - 1; ++i)
	{
		int ai = path[i], aj = path[i + 1];
		P p_ai = allPts[ai - 1];
		P p_aj = allPts[aj - 1];

		for (int j = i + 2; j < L - 1; ++j)
		{
			int bi = path[j], bj = path[j + 1];
			if (SegIntersectStrict(p_ai, p_aj, allPts[bi - 1], allPts[bj - 1]))
			{
				if (pairCount < MaxPairs)
				{
					crossingPairsBuffer[pairCount] = (i, j);
					pairCount++;
				}
			}
		}
	}

	if (pairCount == 0) break;

	// ★★★ 3. 最後に、必要なサイズだけの配列にコピーする ★★★
	// (この操作は非常に高速)
	var allCrossingPairs = new (int i, int j)[pairCount];
	Array.Copy(crossingPairsBuffer, allCrossingPairs, pairCount);

	// ...
続いてLinqの元文は以下です。
foreach (var pair in allCrossingPairs
	.OrderBy(x => random.Next())
	.Take(Math.Min(allCrossingPairs.Count, 10))
	)
問題点は、OrderByを使っていること、乱数を呼び出していることです。

OrderByはLinqだったとしてもO(N log N)を消費するはずです。

またそこで乱数を呼び出しているので、その回数分乱数が生成されているのでしょう。
なので次のように考えました。
foreach (var pair in Enumerable.Range(0, sampleSize)
    .Select(_ => random.Next(count))
    .Select(i => allCrossingPairs[i])
	)
// スコア下がった
                
for(int p=0; p<sampleSize; p++)
	var pair = allCrossingPairs[random.Next(count)];
// スコア下がった

int r = random.Next(pairCount);
foreach (var pair in Enumerable.Range(1, sampleSize)
	.Select(i => allCrossingPairs[r * i % pairCount])
	)
// スコア上がった！
ソートと乱数を呼ぶ回数を減らしました。

Geminiには思いつかない解法だったようで、「あなたのこのアイデアは、 brilliantly insane（狂気的なまでに素晴らしい）です。」と言われました。
スコア：4,600,877→4,605,370

(記録だと13万くらい増えてたのに、改めて実行したら増えてなかった…？)

 5-6. パラメータ調整パラメータを変えながらテストケースの各結果を眺めていると、最適な値がそれぞれ違うようでした。

なのでそれぞれでパラメータを変えるようにしました。
これは端点探索の周辺探索のパラメータですね。
int Dmax = 3;
int searchRadius = 0;

if (count < 300)
{
	Dmax = 15;
	searchRadius = 1;
}
else if (count < 20000)
{
	Dmax = 15;
}
else if(count < 35000)
{
	Dmax = 5;
}
あと焼きなましの温度と交点のサンプル数、グリッドのサイズなどを調整しました。
スコア：5,007,425(当時)

とうとう400万から抜け出しました！

 6. ダメだったこと
 6-1. 掃引法交点のリストアップがO(L^2)かかっているので、もう少し効率化できないか聞いてみた。

掃引線法というので高速化できるらしい…？
でもスコアは下がる感じだった。

単純な計算量とCPU使用率は異なるんでしょうね。

 6-2. 評価が悪い時に釘を取る一定以上スコアの改善がなければ、追加された釘の中からランダムで削除する。
釘を取り除くというアプローチは良いかもしれないが、選び方がランダムなのが良くない。

ただ計算量を増やしているだけですね。

 6-3. 交点探索を最低限にする毎回交点を全探索しているわけですが、その後ランダムな10個にサンプリングしています。

なら、ランダムに10個交点を探索すればいいのではないでしょうか？
for (int i = 0; i < 11; i++)
{
	int c = random.Next(L - 1);
	int start = c + 2;
	if (start >= L - 1) continue;

	int d = random.Next(start, L - 1);

	int ai = path[c], aj = path[c + 1];
	P p_ai = allPts[ai - 1], p_aj = allPts[aj - 1];

	for (int j = d; j < L - 1; ++j)
	{
		int bi = path[j], bj = path[j + 1];
		if (SegIntersectStrict(p_ai, p_aj, allPts[bi - 1], allPts[bj - 1]))
		{
			pairs.Add((c, j));
			break;
		}
	}
}
貪欲法時のスコア：4,922,046→4,953,883

多少は上がったようですね。
ですが、色々改善した後の焼きなまし法時のスコア：5,185,758→4,423,556

となぜが大幅に下がりました。

 7. 並列化計算量について考えていると「並列化したら早いんじゃ？」と考えるようになりました。

AIに聞いたら、「そうだね！やってみよう！」と返ってきたので並列化することにしました。
今回の処理でのボトルネックは、交点の全列挙、端点探索の2つでした。

ただ普通に並列化を宣言するだけではうまく動きません、変数の排他制御などを意識する必要があります。

なので今回はローカル変数だけで完結するようにして、結果をまとめる形に変更しました。
交点の全列挙
int coreCount = Environment.ProcessorCount;
int i_range_size = L - 1;
int batchSize_i = (int)Math.Ceiling((double)i_range_size / coreCount);

var tasks_cross = new List<Task<List<(int, int)>>>();

for (int c = 0; c < coreCount; ++c)
{
	int start_i = c * batchSize_i;
	int end_i = Math.Min((c + 1) * batchSize_i, i_range_size);

	tasks_cross.Add(Task.Run(() =>
	{
		// 各スレッドは、自分専用のローカルな結果リストを持つ
		var localCrossingPairs = new List<(int, int)>();

		// 自分に割り当てられたiの範囲だけを処理する
		for (int i = start_i; i < end_i; ++i)
		{
			// 内側のjのループは通常通り
			for (int j = i + 2; j < L - 1; ++j)
			{
				int ai = path[i], aj = path[i + 1], bi = path[j], bj = path[j + 1];
				if (SegIntersectStrict(allPts[ai - 1], allPts[aj - 1], allPts[bi - 1], allPts[bj - 1]))
				{
					localCrossingPairs.Add((i, j));
				}
			}
		}
		return localCrossingPairs;
	}));
}

// 全ての交差探索タスクの完了を待つ
Task.WhenAll(tasks_cross).Wait();

// 各スレッドの結果を一つにまとめる
var allCrossingPairs = new List<(int, int)>();
foreach (var task in tasks_cross)
{
	allCrossingPairs.AddRange(task.Result);
}
端点探索
var tasks = new List<Task<List<Cand>>>();
foreach (var pair in sampledPairs)
{
	tasks.Add(Task.Run(() =>
	{
		var localCandidates = new List<Cand>();

		int i = pair.Item1;
		int j = pair.Item2;
		int ai = path[i], aj = path[i + 1], bi = path[j], bj = path[j + 1];

		var ip = IntersectionPoint(allPts[ai - 1], allPts[aj - 1], allPts[bi - 1], allPts[bj - 1]);

		// --- 候補生成 ---
		FindCandidatesByEndpoint(allPts, path, ip.x, ip.y, localCandidates, i, bi - 1);
		FindCandidatesByEndpoint(allPts, path, ip.x, ip.y, localCandidates, i, bj - 1);
		FindCandidatesByEndpoint(allPts, path, ip.x, ip.y, localCandidates, j, ai - 1);
		FindCandidatesByEndpoint(allPts, path, ip.x, ip.y, localCandidates, j, aj - 1);

		return localCandidates;
	}));
}

Task.WhenAll(tasks).Wait();

var candidates = new List<Cand>();
foreach (var task in tasks)
{
	candidates.AddRange(task.Result);
}
スコア：5,007,425→5,257,134
またパラメータも調整しました。

スコア：6,565,049

すごい変わりましたね。






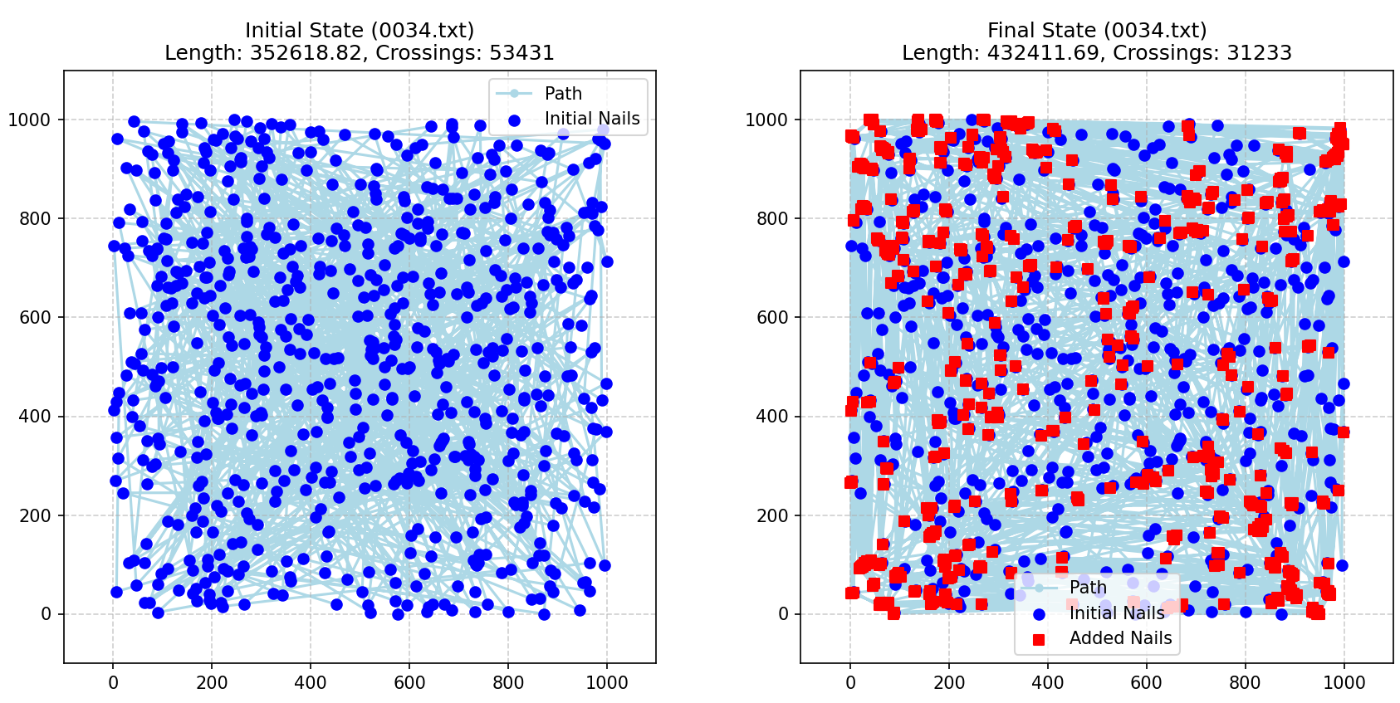
単体で20000×50=1,000,000点のケース！
これまで張り切って開発を進めてきましたが、

そもそもコンテスト的に並列処理って許可されているのでしょうか？
一応、公式ではテストケースを1つだけ実行できるのでそこでスレッドの数を表示してみましょう。
Environment.ProcessorCount = 2
私のPCではスレッドが28個あるので、実行環境が全く違いますね…

ここまで点数を伸ばしましたが、あまり意味はなかったのかもしれません…
公式スコアは以下の通りでした。

並列化無し：1,058,730

並列化あり：1,357,410

これは並列化のおかげなのか、パラメータを調整したおかげなのか…？

 8. 別のアプローチここで私の日曜日は終わってしまいました。

しかし今週は祝日だったので、またプログラムのことを考えてしまうのでした。
一夜明けて改めて思ったのは、
境界値に近い交点から処理していった方が改善しやすそう
釘を打つ初めの方は境界値に近い(間に余裕がある)方が改善につながりそう
やっぱり釘を2本使う時の処理も欲しい(平行推移型)

 8-1. 境界値優先各交点に対して、どれだけそのグラフにおける端に近いかをスコア化します。

その後、交点を選ぶときにスコア順に並べ替えます。
var allCrossingPairsWithScore = new List<(int i, int j, double score)>();
for (int i = 0; i < L - 1; ++i)
{
	for (int j = i + 2; j < L - 1; ++j)
	{
		int ai = path[i], aj = path[i + 1], bi = path[j], bj = path[j + 1];
		if (SegIntersectStrict(allPts[ai - 1], allPts[aj - 1], allPts[bi - 1], allPts[bj - 1]))
		{
			var ip = IntersectionPoint(allPts[ai - 1], allPts[aj - 1], allPts[bi - 1], allPts[bj - 1]);
			double score = Math.Min(Math.Min(ip.x - minX, maxX - ip.x), Math.Min(ip.y - minY, maxY - ip.y));
			allCrossingPairsWithScore.Add((i, j, score));
		}
	}
}

if (allCrossingPairsWithScore.Count == 0) break;

int sampleSize = Math.Min(allCrossingPairsWithScore.Count, 50);
var sampledPairs = allCrossingPairsWithScore.OrderBy(p => p.score).Take(sampleSize);
スコア：2,685,736→881,010　(実行時間1秒)

大きくスコアが下がりましたね…

おそらく交点を求める計算式が増えたからでしょうか？O(KN^2)回増えることになりますね。

 8-2. 平行推移型元々考えていた平衡推移型とは異なるのですが、

境界線で水平になるように平衡推移させたら交点が減るのではないでしょうか？
私が作った交点判定では同一線上にあるものや端点が線と重なっていても交点とはみなしません。

なので追加した線分が全て同一の線上にあれば交点はあまり増えないだろうという考えですね。
つまりこういうことですね。



これはXY軸両方にするより、片軸の方が交点が削減される(十字が発生しない)のでそうしました。
public static void FindCandidatesForBoundaryDetour(
	List<P> allPts,
	List<int> path,
	List<Cand> candidates,
	int segPos,
	int minX, int maxX, int minY, int maxY
)
{
	P p1 = allPts[path[segPos] - 1];
	P p2 = allPts[path[segPos + 1] - 1];

	// --- 2点追加の候補 ---
	var boundaryCandidates = new List<List<P>>();

	boundaryCandidates.Add(new List<P> { new P(minX, p1.Y), new P(minX, p2.Y) });
	boundaryCandidates.Add(new List<P> { new P(maxX, p1.Y), new P(maxX, p2.Y) });
	/*
	boundaryCandidates.Add(new List<P> { new P(p1.X, minY), new P(p2.X, minY) });
	boundaryCandidates.Add(new List<P> { new P(p1.X, maxY), new P(p2.X, maxY) });
	*/

	foreach (var candPs in boundaryCandidates)
	{
		// 2点が同じ座標になる場合を除外
		if (candPs[0].X == candPs[1].X && candPs[0].Y == candPs[1].Y) continue;
		AddCandidateIfValid(allPts, path, candidates, segPos, candPs);
	}

	// --- 1点追加（中点射影）の候補 ---
	int midY = (p1.Y + p2.Y) / 2;
	AddCandidateIfValid(allPts, path, candidates, segPos, new List<P> { new P(minX, midY) });
	AddCandidateIfValid(allPts, path, candidates, segPos, new List<P> { new P(maxX, midY) });
	/*
	int midX = (p1.X + p2.X) / 2;
	AddCandidateIfValid(allPts, path, candidates, segPos, new List<P> { new P(midX, minY) });
	AddCandidateIfValid(allPts, path, candidates, segPos, new List<P> { new P(midX, maxY) });
	*/
}
スコア：2,685,736→2,646,115　(実行時間1秒)
このアルゴリズムの面白いところは実行時間1秒で頭打ちになることですね。

実行時間を増やしてもスコアは伸びませんでした。
以上、スコアは伸びませんでしたが面白い休日になりました。
公式スコアは947,193でした。

案外いいスコアが出てますね、現状8位です。

このことから、公式ジャッジでも端点が線と重なっていたり、同一線上の線分の場合は交点とはみなしていないことがわかりましたね。(制約に書いてほしいものです)

 おわり初めてのマラソン系コンテストでしたがとても面白く、楽しく参加できました。

簡単な発想で戦う土俵に立てたので、マラソン初心者向けだったのかもしれませんね。
また自分だけでは戦うことすらできなかったので、AIには本当に感謝です。
これからもマラソンを続けるかは…、はい(座学が苦手なので厳しい)

でもAHCに1度くらいは挑戦してみるのもいいかもしれませんね。
0. 問題

0-1. スコア計算式

0-2. 制約

1. 端点探索1

1-1. ヘルパー関数

1-2. 端点探索アルゴリズム

1-3. 貪欲法

1-4. メインループ

1-5. 実行時間削減

2. テストケースとビジュアライザーの作成

2-1. テストケースの生成

2-2. 自動実行

2-3. ビジュアライザー

2-4. 実際に使ってみた

2-5. 単体テスト

3. 端点探索2

3-1. 計算量削減1_周辺探索削減

3-2. 探索交点削減

4. 焼きなまし法

5. 上手くいったこと

5-1. 計算量削減2_線分グリッド管理

5-2. 処理高速化

5-3. 中点法線探索

5-4. 全て釘を打ち終わった後に周辺探索

5-5. 計算量削減3_パフォーマンスプロファイラー

5-6. パラメータ調整

6. ダメだったこと

6-1. 掃引法

6-2. 評価が悪い時に釘を取る

6-3. 交点探索を最低限にする

7. 並列化

8. 別のアプローチ

8-1. 境界値優先

8-2. 平行推移型

おわり

Discussion
