Pythonで点群処理ワンライナー
はじめに
2022年も終わりますね。
今年は点群処理が網羅的に解説された本が出たり、テキストから点群生成できるAIが出てきたり、いろいろ点群界隈も盛り上がっていたかと思います。
そんな正統派点群技術が盛り上がった年の最後に、闇の点群技術を紹介できればと思います。
Pythonワンライナーの世界
Pythonワンライナーとは、普通に書くと数行に渡りそうな処理をワンライナー(一行)で書くことで、ただただ自己満足・自己顕示欲のためだけに難解なコードを作成するアレなテクニックです。
この記事では一般的なPythonワンライナーコードではなく、点群処理に特化したアルゴリズムのワンライナーを紹介していきたいと思います。
前提条件
まず、本記事のテクニックではnumpyおよびscipyのみライブラリとして使用することを許可しています。
Open3Dまで使ってしまうと闇どころか完全なチートになってしまうのでこちらは使用しないとします。
forやリスト内包はなるべく使わない
基本的なところなのですが、forやリスト内包はnumpyのベクトル化の機能で代替できる場合が多いのでなるべく使わないこととします。
for文っぽいものを使いたい場合は、mapやnumpy.frompyfuncなどを使うようにします。
基本的な闇Pythonテクニックを叩き込んでおく
以下のサイトを参考に基本的な闇Pythonテクニックを学んでおきます。
またnumpyのスライス処理も重要なので使い方を覚えておくと良いです。
点群処理ワンライナー
KNN(K Nearest Neighbor)
点群に対しとあるクエリの点を与えて、その近傍K個の点を取ってくるアルゴリズムです。
点群処理の基本となるものなので、まずはここからワンライナー化してみます。
from scipy.spatial import cKDTree
points = np.array([[1.0, 2.0, 3.0], [...],...]) # Nx3 matrix
k_neighbar = 10 # 点の数の閾値
point = np.array([0.1, 0.2, 0.3]) # クエリとなる点
# 以下がKNNの処理
neighbars = points[cKDTree(points).query(point, k_neighbors)[1], :]
最近点の計算にscipyのKDTreeを用いています。
KDTree.queryは最近点の距離とインデックスを返すので、インデックスの方だけを取り出して、numpyのスライスによって最近点を取り出しています。
Radius Outlier Removal
点群処理のノイズ除去で使用されるアルゴリズムです。
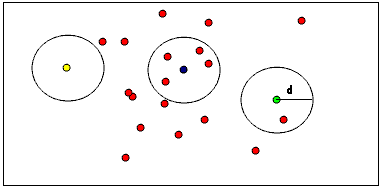
点群中のとある点に着目した際に、その点の一定半径d内に他の点が何個あるかで、その点がノイズであるかを判定する方法です。
PCLのRadiusOutlierRemovalのドキュメント
アルゴリズムのイメージとしてはこの記事に載っている絵が分かりやすいです。
from scipy.spatial import cKDTree
points = np.array([[1.0, 2.0, 3.0], [...],...]) # Nx3 matrix
neighbar_counts = 10 # 点の数の閾値
radius = 0.3 # 点の数を数える円の範囲の半径
# 以下がRadius Outlier Removalの処理
filtered_points = points[list(map(lambda x: len(x) > neighbor_counts, cKDTree(points).query_ball_point(points, radius))) , :]
実装のポイントはさきほどのscipyのcKDTreeの戻り値をそのままmapに食わせているところです。
このようにKDTreeの最近点の計算結果をうまく組み込むことで複雑な処理を一行で書くことができます。
Statistical Outlier Removal
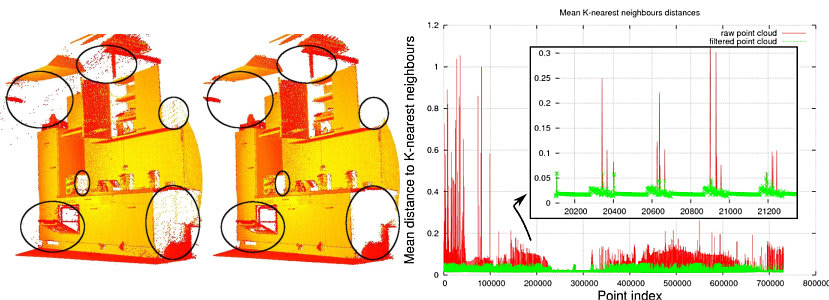
こちらも点群のノイズ除去アルゴリズムですが、統計的な情報を用いた手法です。
点群中のとある点に着目した際に、その点に近い順にK個の点を取得し、着目した点がK点の分散を考えた時に外れ値とみなせるかどうかによってフィルタリングを行っています。
PCLのStatisticalOutlierRemovalのドキュメント
from scipy.spatial import cKDTree
points = np.array([[1.0, 2.0, 3.0], [...],...]) # Nx3 matrix
k_neighbors = 20 # 分散計算を行う近傍点の数
std_ratio = 0.5 # 外れ値と見なす分散の割合
# 以下がStatistical Outlier Removalの処理
filtered_points = points[(lambda x=(lambda x=cKDTree(points).query(points, k_neighbors)[0]: (x.mean(axis=1), x.std(axis=1)))(): x[0].mean() + std_ratio * x[1] > x[0])(), :]
こちらはRadiusOutlierRemovalのときと異なり、mapを使わずにnumpyのベクトル計算の機能を使っています。
lambdaのデフォルト引数を多段で用いることでmeanの計算回数を最小限にしています。
Voxel Grid Filter
点群処理で用いられるダウンサンプリング手法の一種です。
点群をボクセルで区切り、そのボクセル内にある点群の平均となる点を求めることで、元の点群の情報を極力残しつつ、少ない点群にフィルタリングします。

from itertools import groubpy
points = np.array([[1.0, 2.0, 3.0], [...],...]) # Nx3 matrix
voxel_size = 0.2 # ボクセルの辺の長さ
# 以下がVoxel Grid Filterの処理
filtered_points = np.array([np.mean(list(map(lambda v: v[1], values)), axis=0) for _, values in groupby(sorted(list(map(lambda p: (tuple(p[0].tolist()), p[1]), zip(np.frompyfunc(lambda x: np.floor(x / voxel_size).astype(np.int32), 1, 1)(points).astype(np.int32), points))), key=lambda pair: hash(pair[0])), lambda pair: pair[0])])
若干ややこしいので、分解しながら説明します。
まず、やりたいこととしては、各ボクセルのインデックス(intの3要素タプル)を各点から求めます。
それが以下の部分になります。(この段階ではまだタブルでは無くintの3要素のndarray)
np.frompyfuncでベクトル関数化したものにpointsを代入し、最後intに変換します。
np.frompyfunc(lambda x: np.floor(x / voxel_size).astype(np.int32), 1, 1)(points).astype(np.int32)
次に、ここで作ったインデックスと各pointのペアの配列を作成し、インデックスでソートします。
sorted(list(map(lambda p: (tuple(p[0].tolist()), p[1]), zip(np.frompyfunc(lambda x: np.floor(x / voxel_size).astype(np.int32), 1, 1)(points).astype(np.int32), points))), key=lambda pair: hash(pair[0]))
ソートするために、タプルのハッシュをキーに指定しています。
最後にitertoolsのgroupbyを用いて、同じキーの点をグルーピングし、グループ内で平均をとって終了です。
実際の点群で計算した結果は以下のようになります。
オリジナル

VoxelGridFilter後

まとめ
正直こういった処理がワンライナーで書けるのもほぼnumpy/scipyの配列の処理に対する表現力の高さのおかげかなと思っています。
(ちなみに今回のワンライナーでサイズの大きな点群はめちゃメモリ食います。)
ワンライナー化を考えながらいろいろとまだ知らないpythonやnumpyの機能を知ることができました。
今回のコードをそのまま実際の点群処理のコードで用いることはないと思いますが、遊びとしてパズルみたいな感じで点群処理ワンライナーコードを楽しんでもらえればと思います。
Discussion