牛耕式を日本語に当てる
牛耕式とは
あのイーハトーヴォの
で夏、風たっおときす
も底に冷たさをもつ青
森いしくつう、らそい
で飾られたモリーオ市
かひらぎらぎの外郊、
る草の波。
のように奇数行は左から偶数行は右から書く方式で目の移動を最小にできる長所を持つ記法
Dvorak配列と近い匂いを感じる
そこでColemak配列に当たる代物を作ろうとの試み
提案手法 否定書き
まず日本語は珍しく縦書きも横書きも普及していてこれを利用しない手はない
また右から左へ書いていく方式は馴染みがないからやめる
つまり
- 左から右端
- そのまま下端へ
- 左上に戻る
という否定記号¬のように読んでいく方式を提案する
名前は否定書きとしておく
先の例に当てると
あのイーハトーヴォの
風、夏でも底に冷たす
いそら、うつくしさき
られたモリーオいをと
外のぎらぎら市森もお
る草の波。ひ、でつっ
か郊飾青た
慣れ親しんだ横書きと縦書きから成っていて読みやすい
とまではいかなくとも牛耕式よりは幾分よいのではないだろうか
目線の移動量については実感が湧かないだろうから目を移す文字数で計算してみる
視線移動文字数の計算
このプログラムを用いて計算とプロットを行った
- 1文字右へもしくは下へ目を移すと1増える
- 斜めに移動する場合は縦と横の文字数の2乗和の平方根をとる
それらの総和を視線移動文字数とし比較をすると下の画像のようになる
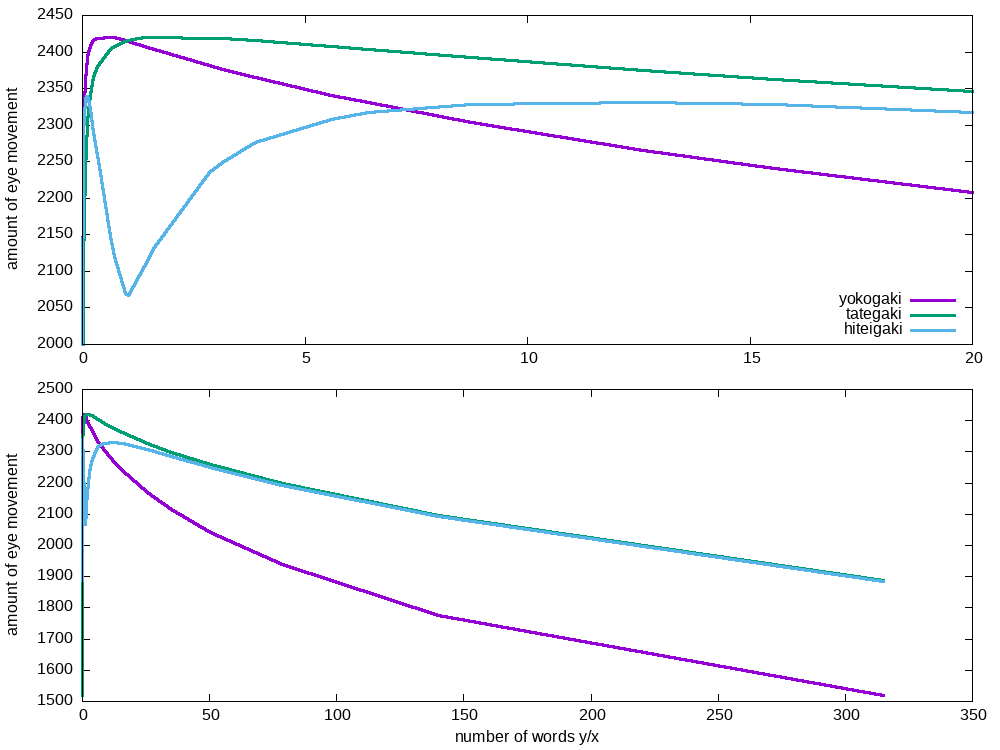
今回は高度合成数から1260文字で固定して縦の文字数を横の文字数で割ったものを横軸にし視線移動文字数を縦軸に置いた
縦の文字数が横の文字数より6.43倍までは否定書きの方が視線移動文字数が少ないわけだから有用な気もするがいかんせんこんな比率で書くことも無いのだろうし具体例でみたほうが実感が湧いて良いかもしれない
実用の上で
新書
手元の新書42行16列を利用すると横書き1246.365152縦書き1271.182900禁止書き1167.660476となり禁止書きが優勢
文庫
これまた手元にあったものでは38行16列で横書き1126.231966縦書き1147.202666禁止書き1045.636821で相変わらず
横書きの単行本
35行36列で横書き2415.485615縦書き2414.514595禁止書き2069.214987となり同様
note
16:9FHDのディスプレイで初期状態のChromeを用いたところ28行34列となり横書き1815.408997縦書き1809.610902禁止書き1572.829309でWEBでも通用するよう
同じ環境でTwitterをみると5行33列で横書き263.939380縦書き288.062485禁止書き278.493361となり普通の横書きの方が良い感じ
またiPhone11のアプリ6行26列も横書き275.099960縦書き257.475488禁止書き65.614259で縦書きが良いなんて結果に
使えるのか
慣れることで横書きや縦書きと遜色なく読めるのであれば視線移動文字数が減っている以上は効率的と言えるかもしれない
ただ私は医学に明るくないので視線の移動がどのように起こっているかも知らず正しい計算かは確かでない
またインターネットが今ほど普及していない2007年の調査日本人の読書離れは進んでいるのかにおいても読書よりインターネットに時間が割かれており現代ではこの傾向が顕著になっていると考えられWEBへの対応がより肝要と考える
頁による隔たりのないため単純に文字数から縦横比を選ぶのではなく画面に表示される文字数に応じてレンダリングしていく必要がある
これに違和感なくスクロールを落とし込むと手法が思いつかないがスクロールしたら書いてある文の全てを更新するくらいだろうか
本に関しても縦書きが混じるため数式や英語を使えないといった問題も生じる
また文章が避けるような画像の配置をすることにも困難が伴うだろう
WEBなら簡単に作れるので取り敢えず試すのが肝要に思える
試す
簡単に作ったものとそのコード
面倒なのでスマートフォンには対応しておらずマウスのスクロールによって次が読める
次を読もうと右下から左上に視線をやるとどこまで読んでいたかがわからなくなり全く読みにくい
試してみないとわからなかったので作った甲斐があった
総じて
視線移動文字数からは楽に読めるであろうと考えられた禁止書きだが実際に試すと読みにくく良い書き方とは言えないだろう
この結論に落とし込むと文章は書けるのにやたら無知な読書感想文賞レース常連小学生かストーリーの為に頓痴気な予想をたてる卒研生のようで嫌だ
そもそも牛耕式のメリットは視線の移動量よりも文章に関係ない部分のために目線を動かす必要がない点にあるなんてわかりきっていたことなのだから
無為

Discussion