浅いニューラルネットワークで作る高精度なオセロの評価関数
コンピューター将棋やチェスで主流のNNUEのような、浅いニューラルネットワークを利用したオセロの評価関数の実装に挑戦しました。リポジトリは以下からご覧いただけます。
-
オセロプログラム
リリースページでは、Windows 向けの CUI / GUI プログラム(CPU が AVX2 に対応している必要があります)と、重みファイルをダウンロードできます。 -
学習用コード
ニューラルネットワーク
StockfishのNNUEをベースにしたアーキテクチャになっています。異なる部分について簡単に解説します。
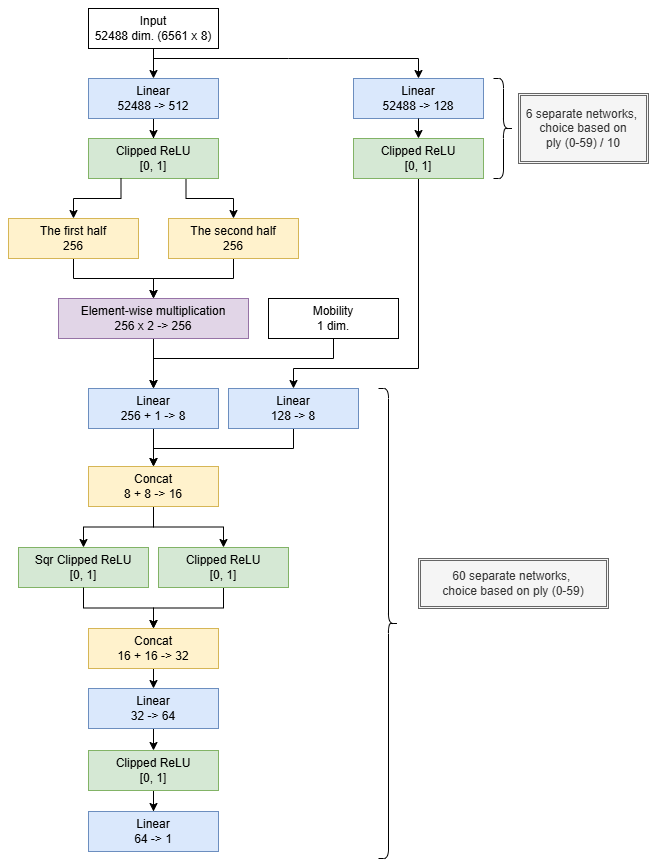
特徴量
ニューラルネットワークの入力特徴量として、「パターン」と「着手可能数」の2つを採用しました。
盤面の局所パターン
オセロ盤は8×8のグリッドですが、その全体を評価するのは難しいため、まず「局所パターン」として、小さなマスの集まり(例:2×2、3×3、または直線状の連続マスなど)を対象にします。これらのパターンは、角や辺、中央部など戦略的に重要な領域の特徴を捉えるために選ばれています。各マスは、石が黒、石が白、または空きの3状態を取り、たとえば、2×2パターンであれば3^4=81通りの組み合わせとなります。
パターンについてはこちらがわかりやすいと思います。
今回利用したパターンは以下の8個(2種類×4セット)です。
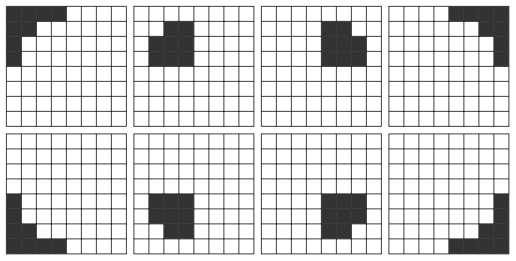
パターンの線形和による評価関数では40個以上のパターンを用いることが一般的です。ニューラルネットワークの場合はパターン同士の関係性から重要な盤面の特徴を学習できるはずなので、盤面全体をカバーしつつ、それ自体が多少は戦略上の意味があると考えられる最低限のパターンのみに絞りました。オセロは一手ごとの盤面変化が大きく、NNUEの"UE(効率的に更新可能)"を実現するのが難しい?ため、パターンが多いと推論時の計算コストが大きくなり、NNUEのような隠れ層の大きさは難しくなります。ネットワークサイズをある程度大きくしつつ計算コストを抑えるためにも、パターン数を少なくすることにしました。
なお、NNUEでは手番側と非手番側で別々のネットワークを持ちますが、パターンには両方の情報が含まれているため、特に分けていません。
着手可能数
着手可能数とは盤面上の石を置くことができるマスの数のことです。着手可能数は非常に優秀な特徴として知られていますが、前述のパターン8個だと着手可能数を上手く学習するのが難しそうです。ニューラルネットワーク全体に比べれば着手可能数の算出コストは無視できる程度なので、追加してみました。2層目からの入力になっているのは、1層目が学習するであろう特徴と同レベルの特徴と考えられるということと、計算量が小さくなるためです(512 vs 8)。
フェーズ別ネットワーク
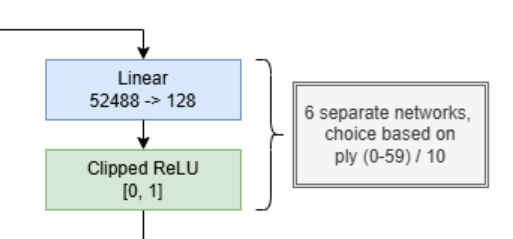
序盤・中盤・終盤で異なる特徴に注目できるよう、フェーズ別のネットワークを追加しました。10手ごとに対応するネットワークを切り替えることで、単純に隠れ層を大きくするよりも推論時の計算コストを抑えつつ精度を向上させるのが狙いです。
2層目以降
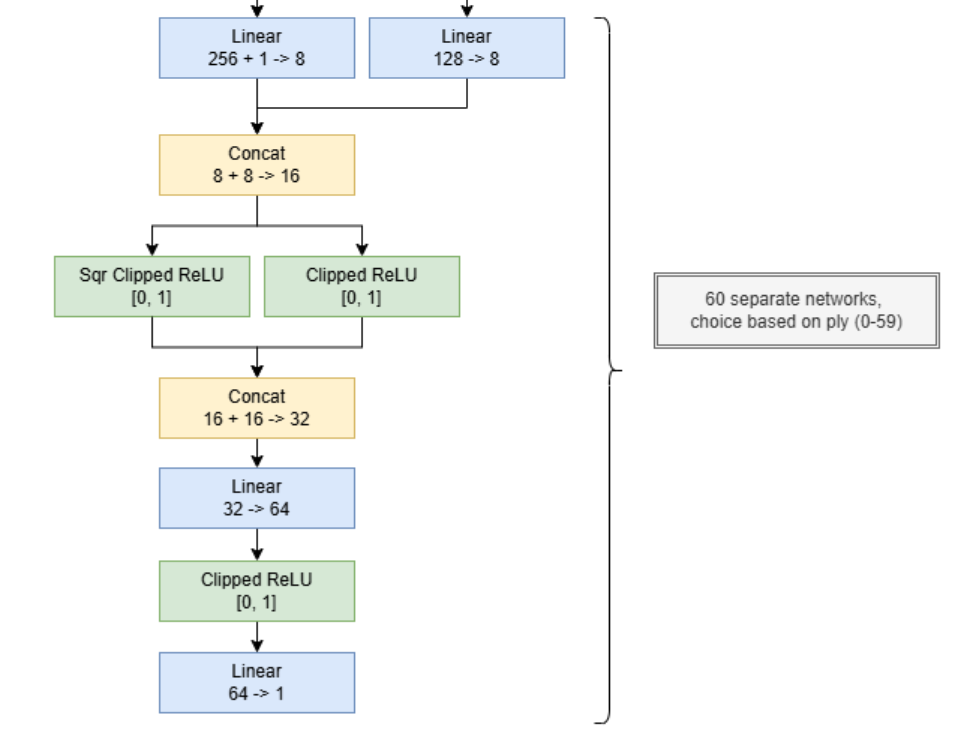
全フェーズ共通のネットワークとフェーズ別のネットワークを結合し、以降の計算を行います。局面の手数(盤面の合計石数 - 4)に応じて60個のネットワークに分岐します。
学習について
学習用コードはStockfishのnnue-pytorchをベースに作りました。
学習データ
1手目から最大30手目までランダムに手を進め、残りを自己対局しつつ、各局面の盤面と評価値を記録しました。全ての局面で最終スコアを教師データとすると序盤から中盤の誤差が大きくなります。そのため、序盤~中盤は最終スコアより(精度が高ければ)評価関数自身の出力の方が正解に近いと仮定し、ランダム局面以外は以下のテキトーな式で補正した値を教師データとしました。
初めにEdaxの12手読みで100万ゲーム生成して学習を行い、その評価関数を使ってさらに150万ゲーム生成して再度学習しました。
量子化認識トレーニング的な丸め処理
Stockfishの方にはありませんが、学習中のネットワークの出力が量子化後の出力に近づくように、順伝播での丸め処理を追加してみました。簡易的なテストでは推論時の精度が向上しましたが、テストサンプルが少ないので十分に確認できているとは言えないです。
オプティマイザー、スケジューラー
オプティマイザーはAdamW、スケジューラーはCosineAnneringを使用しました。正直テキトーです。RangerやSGDも試しましたが、AdamWが一番安定してました。
その他
Leaky Relu(α=0.125, Clipping範囲=[-0.125, 1.0])も試しました。小さいネットワークでは精度が向上しましたが、ネットワークサイズが大きくなるとReLUの方が良さそうでした。Leaky ReLUは計算が複雑化して推論速度が低下するため、精度が向上するとしても微妙なところがあります。また、最初の隠れ層後では効果が見られましたが、それ以降ではあまり効果がありませんでした。
探索・評価関数の実装
Edaxをベースにして、そこにStockfishの探索・評価関数と昔使われていたybwcを混ぜて薄めた感じになってます。特に独自性はありません。プログラミング言語がRustなのは、単に1度使ってみたかったからです。並列処理わかってない。
精度の評価
互角局面集のXOTを使い、有名な強豪ソフトであるEdax、Egaroucidとレベル1(中盤1手、終盤2手読み)で対戦してみました。
※ これはあくまでも評価関数のみの比較であり、コンピューターオセロとしての強さの比較ではありません。
| Engine | Wins | Losses | Draws | Win Rate | Score |
|---|---|---|---|---|---|
| Neural Reversi v0.1.0 | 16992 | 4153 | 423 | 78.8% | 422542 |
| Edax v4.6 | 4153 | 16992 | 423 | 19.3% | -422542 |
| Engine | Wins | Losses | Draws | Win Rate | Score |
|---|---|---|---|---|---|
| Neural Reversi v0.1.0 | 14468 | 6535 | 565 | 67.1% | 244576 |
| Egaroucid for Console v7.5.1 | 6535 | 14468 | 565 | 30.3% | -244576 |
評価関数が重たい分もう少し勝率が欲しい気もしますが、まずまずだと思います。
Edaxリポジトリにあるproblemをprobcut無しで12手読みした結果がこちら。
CPUはIntel(R) Core(TM) i7-12700。※ No.20は6手先までしか読んでません。
| # | Time(s) | Nodes | NPS | Line | Score | Expected |
|---|---|---|---|---|---|---|
| 1 | 0.004 | 28,519 | 6,831,225 | G8 H7 A8 | 14.3 | 18 : G8 |
| 2 | 0.003 | 38,503 | 12,666,293 | A4 B7 A3 | 11.1 | 10 : A4 |
| 3 | 0.006 | 105,571 | 16,622,213 | D1 G1 C1 | 5.5 | 2 : D1 |
| 4 | 0.004 | 30,256 | 8,638,894 | H8 B6 A5 | 5.3 | 0 : H8,A5 |
| 5 | 0.002 | 17,532 | 7,883,093 | G8 | 30.7 | 32 : G8 |
| 6 | 0.006 | 105,535 | 16,505,575 | H3 A7 A8 | 14.6 | 14 : A1,H3 |
| 7 | 0.002 | 31,428 | 12,781,324 | A6 B8 C8 | 4.2 | 8 : A6 |
| 8 | 0.008 | 163,524 | 20,773,921 | E1 H7 G7 | 7.9 | 8 : E1 |
| 9 | 0.004 | 58,072 | 15,855,836 | G7 A3 B2 | -6.8 | -8 : G7,A4 |
| 10 | 0.006 | 104,926 | 17,999,451 | B2 B7 G1 | 11.6 | 10 : B2 |
| 11 | 0.005 | 75,197 | 14,679,746 | B3 A3 A6 | 29.1 | 30 : B3 |
| 12 | 0.005 | 55,044 | 12,092,267 | B7 H2 A7 | -7.8 | -8 : B7 |
| 13 | 0.003 | 28,054 | 9,506,607 | B7 H7 H8 | 12.0 | 14 : B7 |
| 14 | 0.004 | 49,148 | 11,501,181 | A3 A2 A1 | 17.0 | 18 : A3 |
| 15 | 0.013 | 344,937 | 26,588,633 | G3 | 5.3 | 4 : G3,B8 |
| 16 | 0.009 | 176,909 | 20,245,705 | F8 | 22.0 | 24 : F8 |
| 17 | 0.002 | 14,917 | 7,528,135 | F8 | 11.4 | 8 : F8 |
| 18 | 0.006 | 90,128 | 15,949,882 | G2 B7 | -3.5 | -2 : G2 |
| 19 | 0.009 | 143,484 | 16,842,821 | B6 | 4.2 | 8 : B6 |
| 20 | 0.000 | 47 | 560,190 | H5 | 6.0 | 6 : H5 |
| 21 | 0.009 | 180,838 | 21,199,985 | G5 G6 H5 | -2.4 | 0 : G5 |
| 22 | 0.009 | 187,971 | 21,034,073 | G8 | 1.7 | 2 : G8 |
| 23 | 0.006 | 97,252 | 15,944,257 | A2 F2 F1 | 1.4 | 4 : A2 |
| 24 | 0.016 | 356,889 | 22,959,034 | C3 B2 B4 | -1.8 | 0 : C3 |
| 25 | 0.014 | 397,540 | 28,597,531 | G1 B8 A5 | -1.5 | 0 : G1,A5 |
| 26 | 0.045 | 1,762,578 | 39,176,496 | D8 | -2.3 | 0 : D8 |
| 27 | 0.013 | 277,311 | 20,819,925 | B7 H5 H3 | -4.2 | -2 : B7 |
| 28 | 0.026 | 906,892 | 34,844,009 | F1 | -1.0 | 0 : F1,B2,E1 |
| 29 | 0.009 | 148,668 | 16,700,891 | G2 D8 H2 | 6.7 | 10 : G2 |
| 30 | 0.013 | 316,996 | 25,142,848 | G3 H2 | 0.4 | 0 : G3 |
| 31 | 0.016 | 371,785 | 22,776,198 | G6 B7 G4 | -2.0 | -2 : G6 |
| 32 | 0.027 | 1,066,092 | 39,341,510 | G3 G8 F3 | -3.8 | -4 : G3 |
| 33 | 0.021 | 702,498 | 34,245,309 | E7 C7 A3 | -9.6 | -8 : E7,A3 |
| 34 | 0.013 | 331,370 | 25,135,206 | C2 D2 A3 | -3.2 | -2 : C2 |
| 35 | 0.011 | 258,459 | 22,502,873 | C7 D8 G1 | -1.6 | 0 : C7 |
| 36 | 0.027 | 1,097,662 | 40,827,589 | B1 C1 E1 | -2.9 | 0 : B7 |
| 37 | 0.024 | 843,410 | 35,063,045 | H3 | -17.3 | -20 : G2 |
| 38 | 0.013 | 453,561 | 35,201,791 | B2 C8 H2 | 2.7 | 4 : B2 |
| 39 | 0.070 | 4,476,891 | 63,833,299 | A8 B8 C8 | 63.5 | 64 : A8,B1,G1,G5,G6,C8,H3,E8,H4 |
| 40 | 0.010 | 445,122 | 43,375,332 | A2 C1 C7 | 41.5 | 38 : A2 |
| 41 | 0.015 | 504,343 | 33,118,363 | H4 A3 A2 | -0.8 | 0 : H4 |
| 42 | 0.013 | 470,630 | 36,114,798 | C6 C7 A4 | 2.9 | 6 : G2 |
| 43 | 0.011 | 341,526 | 32,333,516 | C7 B8 B7 | -8.5 | -12 : G3,C7 |
| 44 | 0.017 | 593,434 | 35,876,115 | D2 G5 | -15.4 | -14 : D2,B8 |
| 45 | 0.025 | 1,373,875 | 55,014,195 | B2 C1 A6 | 4.5 | 6 : B2 |
| 46 | 0.032 | 1,112,695 | 34,798,361 | B7 B6 A6 | -10.1 | -8 : B3 |
| 47 | 0.008 | 202,580 | 24,321,371 | G2 B8 B7 | 7.0 | 4 : G2 |
| 48 | 0.025 | 1,043,628 | 42,291,012 | F6 G5 G3 | 23.6 | 28 : F6 |
| 49 | 0.038 | 971,116 | 25,486,267 | E1 G6 B2 | 13.6 | 16 : E1 |
| 50 | 0.044 | 1,879,726 | 42,450,232 | D8 E8 G8 | 7.1 | 10 : D8 |
| 51 | 0.023 | 571,846 | 24,907,052 | E2 H2 F1 | 6.7 | 6 : E2,A3 |
| 52 | 0.024 | 805,079 | 33,733,443 | A3 F2 B3 | -0.5 | 0 : A3 |
| 53 | 0.055 | 2,633,811 | 48,269,326 | D8 E8 C1 | -2.9 | -2 : D8 |
| 54 | 0.039 | 2,055,641 | 52,566,544 | F8 G6 G5 | -3.0 | -2 : C7 |
| 55 | 0.080 | 4,796,034 | 59,742,893 | G6 H7 C1 | 0.4 | 0 : G6,B7,E2,G4 |
| 56 | 0.032 | 1,519,690 | 47,346,497 | H5 H4 | -0.1 | 2 : H5 |
| 57 | 0.029 | 1,131,760 | 38,636,247 | A6 B5 B4 | -7.7 | -10 : A6 |
| 58 | 0.024 | 1,100,673 | 45,471,081 | G1 F2 H3 | 1.8 | 4 : G1 |
| 59 | 0.010 | 520,821 | 50,460,305 | G8 E8 H4 | 63.5 | 64 : H4,G8,E8 |
| 60 | 0.018 | 544,678 | 30,780,941 | B8 B3 G2 | 12.4 | 20 : C2 |
| 61 | 0.010 | 246,071 | 25,668,759 | F1 G1 H3 | -8.7 | -14 : H3,G1 |
| 62 | 0.020 | 1,009,542 | 51,185,766 | H7 H5 H2 | 22.5 | 28 : E8 |
| 63 | 0.045 | 1,968,250 | 44,074,047 | B8 H6 D2 | -4.2 | -2 : F2 |
| 64 | 0.059 | 3,330,769 | 56,419,859 | E1 D1 G1 | 15.2 | 20 : B4 |
| 65 | 0.046 | 2,625,363 | 56,669,033 | C8 D8 G1 | 8.7 | 10 : G1 |
| 66 | 0.051 | 3,234,813 | 63,095,895 | H3 B7 A7 | 27.6 | 30 : H3 |
| 67 | 0.057 | 3,581,402 | 62,572,869 | A6 F8 F7 | 18.5 | 22 : H3 |
| 68 | 0.065 | 4,328,544 | 66,922,966 | A4 B3 A6 | 20.7 | 28 : E8 |
| 69 | 0.041 | 1,912,460 | 46,331,329 | H5 F7 E8 | -2.7 | 0 : H3 |
| 70 | 0.014 | 459,212 | 32,685,756 | E8 D8 E3 | -20.6 | -24 : E3 |
| 71 | 0.029 | 1,123,355 | 39,134,198 | F2 H4 D2 | 19.6 | 20 : D2 |
| 72 | 0.069 | 4,718,548 | 68,516,225 | A3 F7 E1 | 22.3 | 24 : E1 |
| 73 | 0.062 | 3,150,545 | 50,565,513 | D8 E8 G4 | -3.4 | -4 : G4 |
| 74 | 0.071 | 4,584,700 | 64,141,773 | B5 B1 C8 | -24.6 | -30 : F1 |
| 75 | 0.061 | 3,110,030 | 50,594,685 | D2 D1 E8 | 9.9 | 14 : D2 |
| 76 | 0.097 | 6,995,352 | 72,062,575 | F7 F8 B6 | 29.8 | 32 : A3 |
| 77 | 0.048 | 2,808,833 | 58,758,754 | B7 | 27.5 | 34 : B7 |
| 78 | 0.075 | 4,204,631 | 55,794,528 | A7 A5 A3 | 3.9 | 8 : F1 |
| 79 | 0.014 | 665,399 | 46,043,912 | D7 H4 H8 | 63.5 | 64 : D7 |
- Best move : 73.4% (58/79)
- Top 2 move : 97.5% (77/79)
- Top 3 move : 100.0% (79/79)
- Score ±3 : 70.9% (56/79)
- Score ±6 : 96.2% (76/79)
- Score ±9 : 100.0% (79/79)
- MAE : 2.26
- Std Dev. : 1.69
まとめ
精度が高い評価関数の作成には成功しました。入力特徴量のパターンの少なさにこだわって作りましたが、色々試した感じではネットワークを小さくしてある程度パターンを追加した方が強そうです。次は、斜め2つ+4辺を加えて試してみる予定。
続き
Discussion