Open2023/08/06にコメント追加1

林貴志『意思決定理論』読書メモ

5章 Savageの主観的期待効用理論

期待効用理論のおさらい

期待効用理論はくじ $L$ への選好に対する理論です．くじ $L$ とはラフに言うと， $p^{L}(x)$ の確率で帰結 $x$ を迎える確率分布のことです．各くじの帰結の集合 $X$ とそのくじの分布 $p^{L}(x)$ は既知であるという前提のもとで，我々はくじに対する選好関係を構築できます．

Von Neumann–Morgensternの定理（通常の期待効用理論）は，くじに対する一定の公理の下で，以下が同値であることを示すものでした．

くじの選好が与えられること
くじ $L$ を期待値の形で効用表現することができる． 具体的には，くじの帰結に対するvNMインデックス $u(x)$ とくじの（既知の）分布 $p(x)$ を用いて， $U(L)=E_{p}[u(X)]$ という形で表現する． $u(x)$ はアフィン変換を許す範囲で一意．

期待効用理論では，くじの顕示選好から，くじの帰結に対する効用関数 $u(x)$ に関する期待値でくじを効用表現できると解釈されるでしょう．

注意して欲しいのは，期待効用理論を満たしていないようなくじの選好も存在するということです．いくつかの公理を満たしているようなくじの選好に対しては，期待効用理論で説明することができますが，そうではないくじの選好（アレのパラドクスなど）を顕示する人だって当然います．逆に，もしあなたが期待効用理論的に生きていきたいのであれば，あなたの意思決定は常にいくつかの公理に従っている必要があります．

Savageの主観的効用理論

一方で，主観的効用理論は行為 $f$ への選好に対する理論です．行為 $f$ とは状態から帰結への写像のことであり， $f: \Omega \to X$ で表せます．我々は状態 $\Omega$ や帰結 $X$ については既知としますが，どの状態が発生するのか・どれだけの（客観的な）確率で発生するのかということについては未知とします．

Savageの定理（主観的効用理論）では，行為 $f$ に対する一定の公理の下で，以下が同値であることを示します．

行為の選好が与えられること
行為 $f$ を期待値の形で効用表現することができる． 具体的には，行為の帰結に対するインデックス $u(x)$ と $\Omega$ 上の確率測度 $p(w)$ を用いて， $U(f)=\int_{x \in X} u(x) p(f^{-1}(x))$ という形で表現する．p(x)は一意． $u(x)$ はアフィン変換を許す範囲で一意．

Savageの定理は，行為の顕示選好から，帰結に対する効用関数 $u(x)$ と状態に対する主観的確率 $p(\omega)$ を用いて行為の効用表現を行うことができると解釈されます．言い換えると，ある人が行為に選好関係を持っているならば，それって状態 $\omega$ に対して何かしらの確率分布を（主観的に）想定しているよねということを含意しています．

期待効用理論との関係

期待効用理論との関係を説明します．仮に， $\Omega$ 上での確率測度 $p(\omega)$ が存在し，なおかつそれが既知であったとしましょう．その場合，行為 $f$ から，帰結 $x$ が起きる確率 $P[f^{-1}(x)] = p(x)$ を求めることができます．
結局， $\Omega$ 上の確率測度が既知であれば，行為 $f$ の選好というのはくじの選好と大差ない訳です．誤解を恐れずに言えば，期待効用理論では，分布が既知なくじの選好を対象にしていたのに対し，主観的効用理論では，分布が未知であり主観的なものとなっているくじの選好を対象にしていると考えられます（当然，このように主張するには，いくつもの公理が必要です）．

もうすこし測度論の言葉で

測度論的確率論における，確率変数 $X$ の定義を思い出すともう少し分かりやすいかもしれません．確率変数 $X$ とは，標本空間 $\Omega$ から $\mathbb{R}$ への（可測）関数でした．ここで， $\Omega$ 上の確率測度 $p$ が定められていれば，確率変数 $X$ の分布 $\mu$ は誘導されます．具体的には， $\mu(x) = p(X^{-1}(x))$ とあらわされます．
本題に戻り，行為 $f$ を確率変数だと考えてみましょう． $\Omega$ 上に確率測度が定義されていれば，行為 $f$ から自然に帰結の分布が誘導される訳で，これはまさに帰結 $X$ 上のくじとなるのです．

今更だけど行為って？

ここら辺までの話をもう少し具体的に考えるとどうでしょうか．

例1

状態集合：｛阪神が勝つ，阪神が負ける｝×｛ガンバが勝つ，ガンバが負ける｝（直積）
帰結集合：｛酒を飲む，酒を飲まない｝
このとき，行為は16種類あり，例えば以下のように選好関係を定義できます．

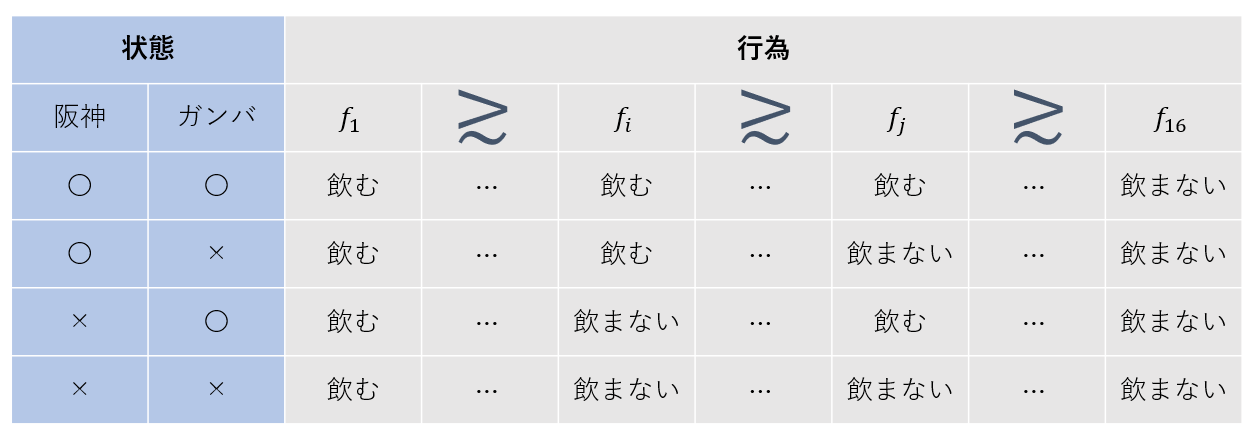
Savageの定理より，この順序が一定の公理を満たしていれば，以下のことが言える訳です．

酒を飲む方が飲まない方が嬉しい（ $u(飲酒) > u(非飲酒)$ ）
この人は阪神の勝率はガンバの勝率より高いと考えている（ $p(阪神勝利) > p(ガンバ勝利)$

メモ：練習問題5.1

（以下は林のテキストを持っていることを前提としている上に，私のメモです）

P1だけを満たさない選好関係

$\Omega=[0, 1], X = [0, 1]$ としたうえで，選好関係を

f \succ g \Leftrightarrow \forall \omega \in \Omega: f(\omega) > g(\omega)

と定義してやると，明らかに完備性を満たさない．が，これはP6も満たさなかった．うーーーん．なんか良い例がないものか．

P3だけを満たさない選好関係

これは帰結の効用が状態と関係しているような例を考える．

$\Omega=[0, 1], X = \{0, 1\}$ としたうえで，選好関係を以下のように定義する．

f \succ g \Leftrightarrow \int_{\omega \in \Omega} v(\omega) f(\omega) d\mu > \int_{\omega \in \Omega} v(\omega) g(\omega) d\mu

ここで， $v(\omega)$ は実数値関数で， $\mu$ はルベーグ測度です．お気持ちとしては，本来は $X=1$ となるときの嬉しさは $\omega$ に依存して欲しくないですが，上の表現をすることで，その嬉しさは $v(\omega)$ という関数になっており，P3に違反させようということです．P6のために積分にしていますが， $\Omega$ を阪神・ガンバの勝ち負けにして，積分をシグマに変えてやると直感的にも分かりやすくなります．

$v(\omega)$ については $v(\omega) = -\omega(\omega-0.9)$ とでもしておきましょう．比較的なんでもいいんですが，どこかの $\omega$ では $v$ が負になってしまうというのが肝です．（P3のために，この関数形にすることで， $1 \succ 0$ になりますが， $E = [0.9, 1]$ とかにすると，P3の左側の選好が成立しないです）

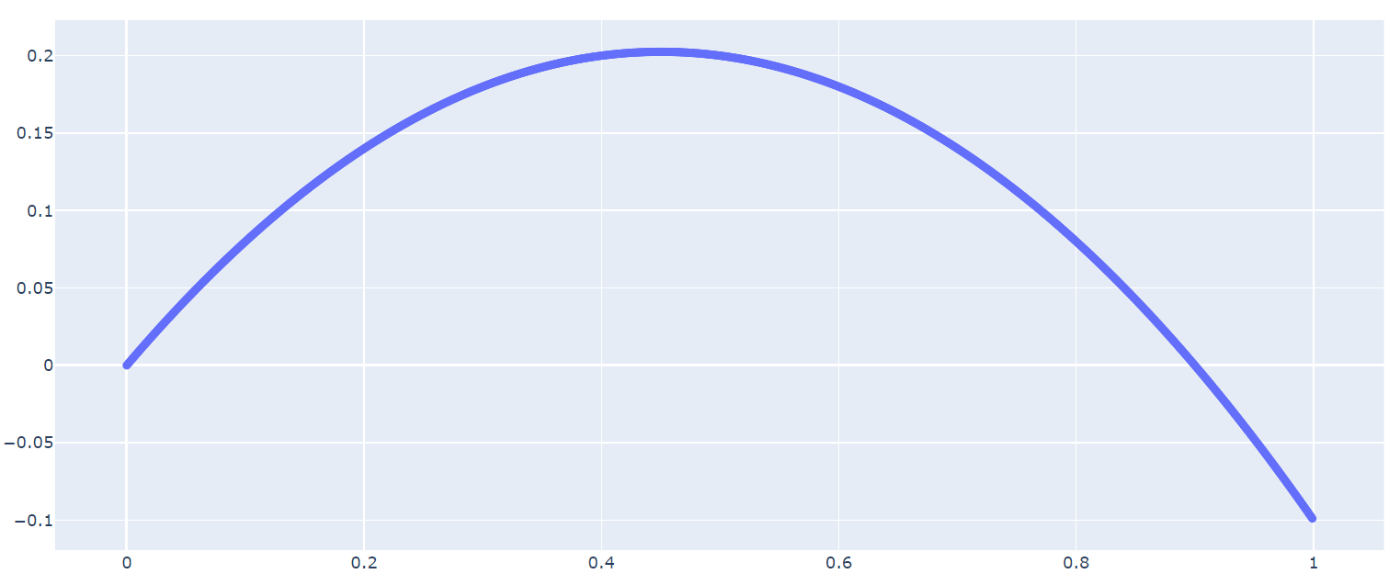
P4は帰結が二つだったら自明に成立し，P2, P5も簡単に示されるのですが，P6が結構厄介です．多分いけるんですけど…