幾何分布と指数分布の関係性について
はじめに
二項分布の試行回数を無限大にするとポアソン分布が導かれること(少数法則)はよく知られています.
実は,試行回数を無限大にすることに関して,以下の関係性も知られています.
- 指数分布が幾何分布から導かれる
- ガンマ分布が負の二項分布から導かれる
ここでは,前者の指数分布から幾何分布から導かれることを示したいと思います.[1]

参考:離散的なコイン投げに関する分布と連続的なイベントの発生の分布の関係性
前提知識
- 負の二項分布は,コイントスにおいて,n回の表が出るまでの試行回数と定義します.[2]
- 確率関数は
p(x) = {}_{x-1}C_{n-1} p^n (1-p)^{x-n} - 累積分布関数は
F(x) = 1 - (1-p)^x x \in \mathbb{N}
- 確率関数は
- 二項分布からポアソン分布を導出することは本記事の前提知識とします.
コイン投げの連続化

コイン投げを連続の時間に拡張していく話をしましょう.
まず,単位時間を
また,
これまでの話を数式でまとめると以下のようになります.
\Delta t \cdot n = 1 p n = \lambda t=\Delta t \cdot x \Delta t \to 0, n \to \infty
このセッティングで,二項分布からポアソン分布を導くことがよく知られています.単位時間でイベントが起きる回数と
幾何分布から指数分布を導出する
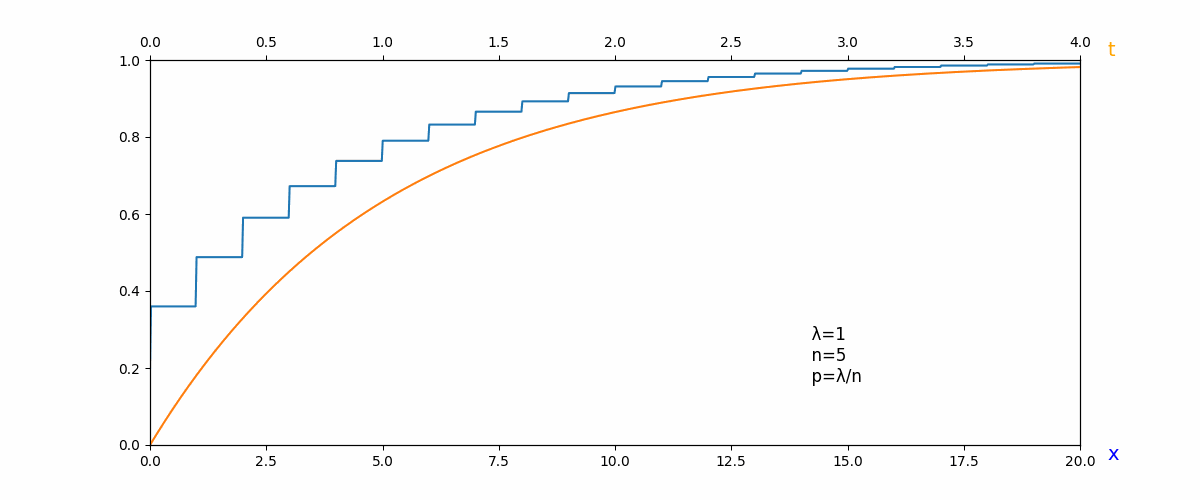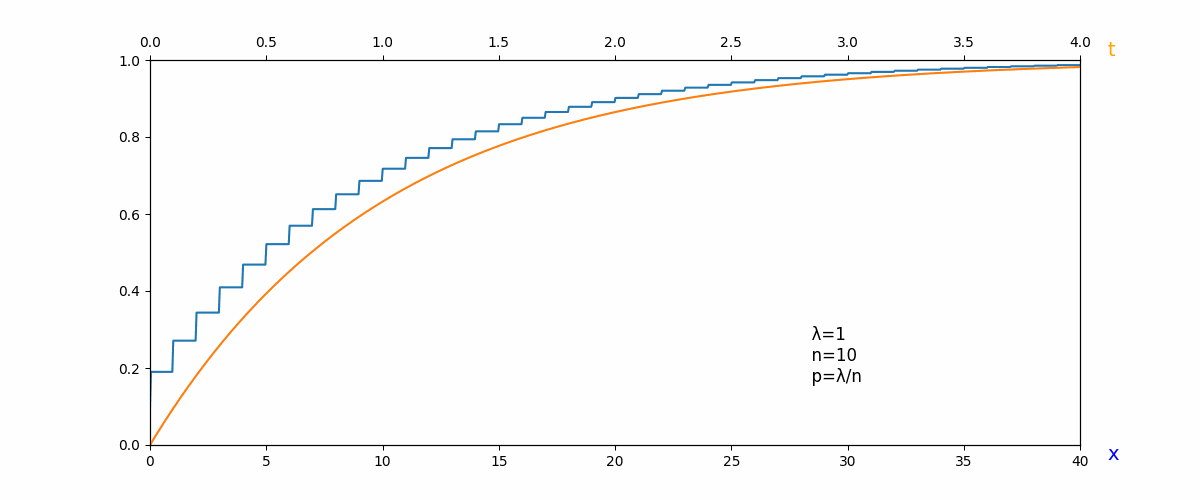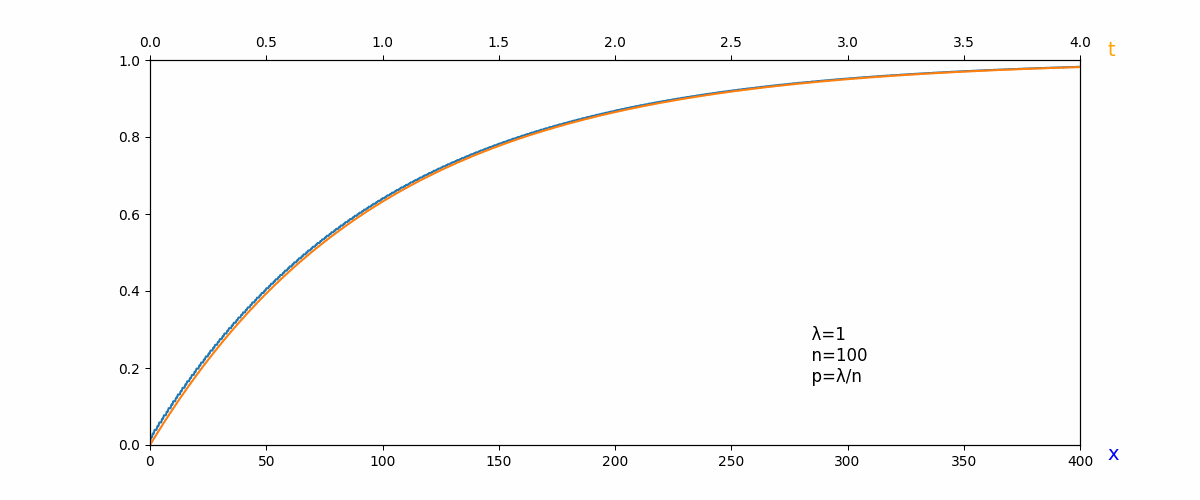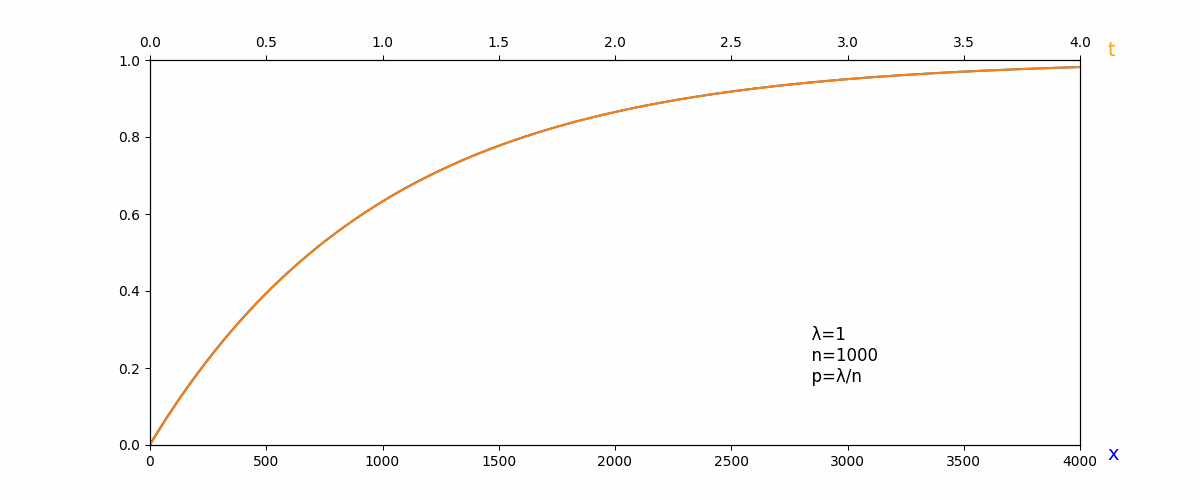
幾何分布の累積分布関数(青)が指数分布の累積分布関数(オレンジ)になっていく様子.
さて,指数分布は最初のイベントが発生するまでにかかる時間
具体的には,最初のイベントが発生するまでに
この発想をもとに,幾何分布の累積分布関数が指数分布の累積分布関数に近づいていくことを示せれば十分です.
よって,
幾何分布から指数分布へのgifコード
まずは画像をつくる
import math
import numpy as np
import matplotlib.pyplot as plt
def F_x(x, p):
"""幾何分布"""
return 1 - (1-p)**(math.ceil(x)+1)
def Ex_t(t, lambda_ex):
"""指数分布"""
return 1 - np.exp(-lambda_ex*t)
lambda_ex = 1
n_list = [5, 10, 100, 1000] # nは単位時間あたりの分割数
image_files = ['image1.png', 'image2.png', 'image3.png', 'image4.png']
frames = []
for i, n in enumerate(n_list):
p = lambda_ex / n # n = λ*pの関係である
delta_t = 1 / n
x_max = 4/delta_t
x_array = np.linspace(0, x_max, 1000)
y_array = np.vectorize(lambda x: F_x(x, p))(x_array) # 幾何分布の累積分布関数
y_array2 = np.vectorize(lambda t: Ex_t(t, lambda_ex))(x_array * delta_t) # 指数分布の累積分布関数
fig, ax = plt.subplots(figsize=(12, 5))
# 折れ線グラフの描画
plt.plot(x_array, y_array)
plt.plot(x_array, y_array2)
ax2 = ax.twiny() # 2つ目のx軸を作成
ax.set_xlim([0, x_max]) # 1つ目のx軸の範囲
ax2.set_xlim([0, 4]) # 2つ目のx軸の範囲
ax.set_ylim([0, 1]) # 1つ目のx軸の範囲
annotation_text = f"""
lambda={lambda_ex}
n={n}
p=λ/n
"""
plt.annotate(
annotation_text, xy=(0.7,0.1), xycoords='axes fraction',
fontsize=12, color='black', ha='left', va='bottom'
)
plt.annotate(
"t", xy=(1.03,1), xycoords='axes fraction',
fontsize=14, color='orange', ha='left', va='bottom'
)
plt.annotate(
"x", xy=(1.03,-0.05), xycoords='axes fraction',
fontsize=14, color='blue', ha='left', va='bottom'
)
frames.append(fig)
GIFにする
from PIL import Image
# 4枚の画像ファイル名をリストに格納する
image_files = ['image1.png', 'image2.png', 'image3.png', 'image4.png']
for i, name in enumerate(image_files):
frames[i].savefig(name)
# 画像ファイルを開いてリストに格納
images = [Image.open(filename) for filename in image_files]
# GIFファイルを作成
images[0].save('output.gif', save_all=True, append_images=images[1:], duration=1000, loop=0)
Discussion