No.11 深層学習の基礎ー(4)畳み込みニューラルネットワーク
::: ⅰ.畳み込みニューラルネットワーク
基本的な畳み込み演算
はい、承知いたしました。
畳み込みの出力サイズについて具体的な計算例を追加し、これまでの全ての情報を統合した最終版を以下に出力します。
(4) 畳み込みニューラルネットワーク(CNN)
この項目は、ディープラーニングの中でも特に画像認識で大きな成功を収めた**畳み込みニューラルネットワーク(CNN: Convolutional Neural Network)**の基本的な仕組みについて学ぶことを目的としています。
核となる考え方:生物の視覚野からのヒント
CNNは、人間や動物が物を見るときに脳の視覚野が働く仕組みを模倣して作られています。この生物学的な背景を理解することが、CNNの各要素の役割を掴む近道になります。
-
受容野 (Receptive Field)
- CNNの出力層の1つの画素(ニューロン)が、入力画像のどの範囲の情報を使って計算されたか、という空間的な広がりを意味します。
- 層が深くなるにつれて受容野は広がり、最初は**「線」や「角」といった単純な特徴から、最終的には「顔」や「猫」**といった高度で複雑な物体全体を認識できるようになります。
-
単純型細胞と複雑型細胞
脳の視覚野にあるこれらの細胞の働きが、CNNの主要な処理のモデルになっています。-
単純型細胞: 視野の**「特定の位置」にある「特定の傾きの線」にだけ反応します。
→ この役割は、画像から厳密な特徴を抽出する「畳み込み層」**が担っています。 -
複雑型細胞: 特徴の位置が多少ズレても気にせず反応できます。
→ この役割は、特徴の位置ズレを吸収する**「プーリング層」**が担っています。
結論として、「畳み込みは単純型細胞から、プーリングは複雑型細胞から着想を得ています」。
-
単純型細胞: 視野の**「特定の位置」にある「特定の傾きの線」にだけ反応します。
CNNを構成する主な要素
- フィルタ / カーネル: 画像から特定の特徴(縦線、特定の色など)を抽出するための「特徴検出器」。
-
パディング (Padding)
- 定義: 入力データの周囲に**0などの特定の値を補う(埋める)**ことです。
-
メリット:
- 端の情報を失わないため: パディングで外側を補うことで、画像の隅々の特徴もしっかりと捉えることができます。
- 出力サイズを調整するため: 畳み込みで画像が小さくなりすぎるのを防ぎ、深いネットワークを構築しやすくします。
- ストライド (Stride): フィルタを画像上で動かす際の「歩幅」。
- チャネル (Channel): 画像の色の層(RGBなど)や、中間層での特徴マップの枚数。
- 特徴マップ (Feature Map): 畳み込み演算によって生成される出力結果。
- im2col: 畳み込み演算を、高速な行列計算に置き換えるための実装上の効率化テクニック。
【最重要】畳み込みの出力サイズの計算
E資格で頻出する、出力サイズを計算する公式とその導出方法、具体例です。
公式
- 入力サイズ:
W(幅),H(高さ) - フィルタサイズ:
FW(幅),FH(高さ) - パディング:
P - ストライド:
S
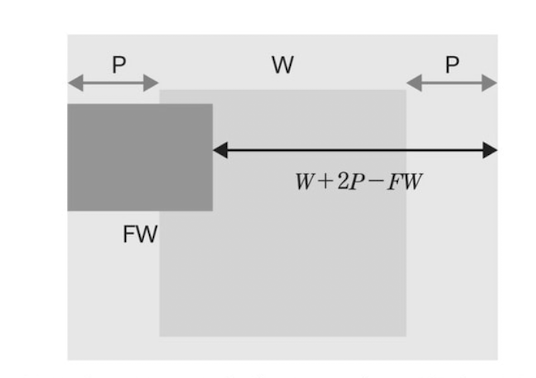
出力サイズOW(幅),OH(高さ) は以下の式で計算できます。([]はガウス記号、またはfloor()関数で小数点以下を切り捨て)
OW = [(W + 2P - FW) / S] + 1
OH = [(H + 2P - FH) / S] + 1
なぜこの式になるのか?
-
全体の長さを求める: 元の幅
Wの両側にパディングPが追加されるので、全体の幅はW + 2Pになります。 -
フィルタが動ける距離を求める: フィルタ自身の幅
FWがあるため、フィルタの左端が動ける全範囲は(W + 2P - FW)となります。 -
移動回数を計算する: この動ける距離を、一歩の大きさであるストライド
Sで割ると、フィルタが何回移動できるかがわかります。(W + 2P - FW) / S -
最初の1回分を足す: 上記は「移動する回数」なので、最初のスタート地点(1回目)の分を
+1します。これが最終的な出力サイズになります。
【具体例】計算してみよう
例1:基本的なケース
- 入力(W): 7x7
- フィルタ(FW): 3x3
- パディング(P): 1
- ストライド(S): 1
OW = (7 + 2*1 - 3) / 1 + 1 = (9 - 3) / 1 + 1 = 6 + 1 = 7
→ 出力サイズは 7x7 となり、入力サイズが維持されます。
例2:ストライドが2の場合
- 入力(W): 7x7
- フィルタ(FW): 3x3
- パディング(P): 1
- ストライド(S): 2
OW = (7 + 2*1 - 3) / 2 + 1 = 6 / 2 + 1 = 3 + 1 = 4
→ 出力サイズは 4x4 となります。
例3:割り切れないケース(切り捨てが発生)
- 入力(W): 6x6
- フィルタ(FW): 3x3
- パディング(P): 0
- ストライド(S): 2
OW = (6 + 2*0 - 3) / 2 + 1 = 3 / 2 + 1 = 1.5 + 1 = 2.5
小数点以下を切り捨てて 1 + 1 = 2...と考えると間違いやすいので、公式に忠実に計算します。
OW = floor((6 + 2*0 - 3) / 2) + 1 = floor(1.5) + 1 = 1 + 1 = 2
→ 出力サイズは 2x2 となります。
E資格でのポイント
- 出力サイズの計算問題は最頻出です。 上記の公式は必ず暗記し、具体例を通してスラスラ計算できるように練習しておきましょう。
- 受容野や単純型/複雑型細胞といった生物学的な背景と、CNNの各層の役割との対応関係を問う問題も出題されます。
特別な畳み込み
** point-wise畳み込み(1x1畳み込み)、depth-wise畳み込み、
Depthwise Separable Convolution 概要メモ
参考記事: https://qiita.com/omiita/items/77dadd5a7b16a104df83
■ 背景
従来の畳み込み層(Standard Convolution)は、計算量とパラメータ数が多く、モデルが大きくなりがち。
特に軽量なモデル(例: モバイル向け)では、効率の良い畳み込み手法が求められている。
■ Depthwise Separable Convolutionとは
Depthwise Separable Convolution(深さ方向分離可能畳み込み)は、標準的な畳み込みを2つの操作に分解して効率化したもの:
-
Depthwise Convolution(深さ方向の畳み込み)
各チャンネルに対して独立に畳み込みを行う(カーネル数 = 入力チャンネル数)。
空間的な特徴を抽出する。 -
Pointwise Convolution(1x1畳み込み)
1x1の畳み込みで、チャンネル間の情報を統合する。
Depthwiseで得られた特徴マップを組み合わせて、出力チャンネル数を調整する。
■ 計算コストの比較
- 標準的な3x3畳み込みと比べて、Depthwise Separable Convolutionでは計算量とパラメータが大幅に削減される。
- 計算量の削減率はおおよそ以下のようになる:
1 / 出力チャンネル数 + 1 / カーネルサイズ²
例)入力・出力チャンネル数が同じで、3x3カーネルの場合、約9分の1の計算量になる。
■ 利用例
- モバイル端末向け軽量CNNモデル(MobileNet、Xception など)で多用されている。
グループ化畳み込み、
アップサンプリングと逆畳み込み
::::
「特別な畳み込み」とは?
一言でいうと、**「普通の畳み込みを進化させて、もっと賢く、もっと効率的にした応用テクニック集」です。
主に、「計算量を減らして軽くする」か「画像のサイズを大きくする」**という特別な目的で使われます。
1. point-wise畳み込み (1x1畳み込み)

1. 前提:通常の畳み込み (左の図)
- 何をやっているか?: 画像の「縦・横(平面方向)」と「深さ(チャンネル方向)」の情報を同時に混ぜ合わせて、新しい特徴(1つの数値)を抽出します。
-
フィルタの形: 例えば
3×3のフィルタなら、そのサイズは縦3 × 横3 × チャンネル数という立体的な形をしています。 -
例えるなら: 材料(ピクセル)を
3×3の範囲で広く集め、ミキサーにかけて新しいジュースを1杯作るイメージです。
2. 1x1コンボリューション (右の図: Pointwise Convolution)
- 何をやっているか?: 縦・横方向には動かず、同じ位置にあるピクセルの「深さ(チャンネル方向)」の情報だけを混ぜ合わせて、新しい特徴(1つの数値)を作ります。
-
フィルタの形:
縦1 × 横1 × チャンネル数という、細長い棒のような形です。 - 別名: Pointwise Convolution (点ごとの畳み込み) とも呼ばれます。まさに画像上の1点(point)だけを見ているからです。
- 例えるなら: ミキサーではなく、各チャンネル(赤、青、緑など)のジュースを決まった割合でコップに注いで、新しい味のジュースを1杯作るイメージです。混ぜ合わせるのは「味(チャンネル)」だけで、「場所(縦横)」は変えません。
3. じゃあ、1x1コンボリューションは何がうれしいの?
この「チャンネル方向だけの演算」には、主に2つの強力なメリットがあります。
-
チャンネル数の調整(次元削減・次元増加)
- 一番重要な役割です。 出力する特徴マップのチャンネル数を自由に変えることができます。
- 例えば、入力が512チャンネルあっても、1x1コンボリューションのフィルタを64個使えば、出力を64チャンネルに減らすことができます。逆も可能です。
- これにより、後続の処理(例えば3x3の畳み込み)の計算量を劇的に削減できます。これがボトルネック構造(MobileNetやResNetなどで使われる)の基本アイデアです。
-
非線形性の追加
- 畳み込み処理の後には、通常ReLUなどの活性化関数を適用します。
- 1x1コンボリューションも立派な「畳み込み」なので、その後に活性化関数を挟むことで、モデルの表現力を(計算コストをあまり上げずに)高めることができます。
一言でまとめると…
1x1コンボリューションは、「画像のサイズは変えずに、チャンネル数を増やしたり減らしたりするための、賢くて計算コストの安いテクニック」です。特に、MobileNetやGoogLeNet(Inceptionモジュール)などの現代的なCNNモデルで、計算量を抑えつつ性能を向上させるために不可欠な要素となっています。
2. depth-wise畳み込み

1. Depthwise Convolution とは?
- 何をやっているか?: 通常の畳み込みとは異なり、チャンネルごとに独立して、縦・横の平面方向の畳み込みを行います。チャンネル間での情報の混ぜ合わせは一切行いません。
-
フィルタの形: フィルタはチャンネルごとに1つずつ用意されます。各フィルタの次元は
縦 × 横 × 1という薄っぺらい形をしています。 -
例えるなら:
- 通常の畳み込み: 複数車線の道路(全チャンネル)を一度に全部見て、1つの情報に集約する。
- Depthwise Convolution: 車線ごとに担当者がいて、自分の車線(チャンネル)の情報だけを見る。担当者同士(チャンネル間)のコミュニケーションはしない。赤色のチャンネル担当は赤色だけ、緑色のチャンネル担当は緑色だけを見て、それぞれ特徴を抽出します。
2. この処理のメリット・デメリット
-
最大のメリット(目的): 計算量を劇的に減らせること。
チャンネルを混ぜ合わせる計算を完全に省略するため、通常の畳み込みに比べてパラメータ数と計算量が大幅に少なくて済みます。これは、スマートフォンなどのリソースが限られたデバイスで高速に動作するモデル(例: MobileNet)を実現するための鍵となります。 -
デメリット: チャンネル間の情報を考慮できないこと。
各チャンネルがバラバラに処理されるため、例えば「赤チャンネルのこの部分」と「青チャンネルのこの部分」を組み合わせた特徴を得ることができません。これではモデルの表現力が不足してしまいます。
3.【重要】Pointwise Convolutionとのコンビネーション
このデメリットを解消するために、Depthwise Convolutionは必ずと言っていいほど「Pointwise Convolution (1x1畳み込み)」とセットで使われます。この組み合わせを**「Depthwise Separable Convolution」**と呼びます。
処理の流れ:
-
Depthwise Convolution (平面方向の処理)
- 各チャンネルで独立して、空間的な特徴(エッジなど)を抽出する。
- 計算コストを大幅に削減!
-
Pointwise Convolution (チャンネル方向の処理)
- ステップ1で得られた各チャンネルの情報を、チャンネル間で混ぜ合わせる。
- Depthwiseの弱点(チャンネル間情報を考慮できない)を補う!
この2段階の処理により、「通常の畳み込みと似たような処理」を、はるかに少ない計算コストで実現することができるのです。これがMobileNetなどの軽量モデルの基本構造です。
一言でまとめると…
Depthwise Convolutionは、「チャンネルごとにバラバラに空間的特徴を抽出することで、計算量を極限まで削減する畳み込み手法」です。単体では性能不足なため、通常はPointwise Convolutionと組み合わせて使われます。
3.「Depthwise Separable Convolution」

1. これは何? 一言でいうと…
通常の畳み込み処理を、**役割が違う2つのシンプルな処理に「分解」**した、非常に賢くて計算コストの低い畳み込み手法です。
2. 分解された2つのステップ
この手法は、以下の2つのステップを順番に行います。
ステップ1: Depthwise Convolution (空間方向の処理)
- 役割: 画像の**「平面方向(縦・横)」**の特徴を抽出する。
- 処理内容: 各チャンネルで独立して畳み込みを行う。チャンネル間の情報は混ぜません。
- 例えるなら: 料理の**「下ごしらえ」**。人参は人参、玉ねぎは玉ねぎで、それぞれ別に切ったり炒めたりする段階。
ステップ2: Pointwise Convolution (チャンネル方向の処理)
- 役割: **「チャンネル方向(深さ)」**の情報を混ぜ合わせる。
- 処理内容: 1x1のフィルターを使って、ステップ1で得た各チャンネルの特徴を統合する。
- 例えるなら: 料理の**「仕上げ」**。下ごしらえした食材を一つの鍋に入れて、味付けし、混ぜ合わせる段階。
3. なぜこの「分解」がすごいの?
-
劇的な計算コスト削減:
「平面の処理」と「チャンネルの処理」を分けることで、通常の畳み込みとほぼ同等の結果を、圧倒的に少ないパラメータ数と計算量で実現できます。 -
軽量モデルの実現:
この効率の良さのおかげで、スマートフォンなどリソースが限られたデバイス上でも高速に動作する、高性能なディープラーニングモデルを作ることが可能になりました。
一言でまとめると…
Depthwise Separable Convolutionは、「①チャンネルごとに平面処理 → ②全チャンネルで深さ処理」という2段階に分けることで、通常の畳み込みを圧倒的に高速・軽量化したバージョンです。
4. グループ化畳み込み
1. これは何? 一言でいうと…
入力チャンネルをいくつかの**「グループ」に分割し、それぞれのグループ内で独立して**通常の畳み込みを行う手法です。
2. 処理の流れ
- 分割: 入力された特徴マップのチャンネルを、複数のグループに分けます。(例:64チャンネルを、32チャンネルずつの2グループに分ける)
- 畳み込み: 各グループの中で、それぞれ独立に畳み込み処理を行います。グループAはグループA内だけで、グループBはグループB内だけで計算します。
- 結合: 各グループの計算結果を、チャンネル方向に連結して、最終的な出力とします。
例えるなら:
会社の仕事を、部署(グループ)ごとに分担して進めるようなものです。営業部は営業部の、開発部は開発部のタスクをそれぞれ独立して行い、最終的に全社の成果としてまとめるイメージです。
3. 通常の畳み込みやDepthwise畳み込みとの違い
この手法は、「通常の畳み込み」と「Depthwise畳み込み」の中間に位置すると考えると分かりやすいです。
-
通常の畳み込み (グループ数 = 1)
- 全チャンネルを一つの大きなグループと見なし、すべてのチャンネル情報を混ぜ合わせて処理します。
- 計算コストが最も高いですが、チャンネル間の情報を最大限活用できます。
-
グループ化畳み込み (1 < グループ数 < チャンネル数)
- いくつかのグループに分けて処理します。グループ内ではチャンネル間の情報が混ざりますが、グループを越えては混ざりません。
- 計算コストと「チャンネル情報をどれだけ混ぜるか」のバランスを取った手法です。
-
Depthwise畳み込み (グループ数 = チャンネル数)
- 各チャンネルを一つのグループと見なす、グループ化畳み込みの極端なケースです。
- 計算コストは最も低いですが、チャンネル間の情報は一切混ざりません。
4. 何がうれしいの? (目的)
-
計算量の削減:
通常の畳み込みより計算量が少なくて済みます。これにより、ネットワークをより**「ワイド(幅広=チャンネル数を多く)」**にすることが可能になります。 -
モデルの表現力向上:
ResNeXtというモデルで採用され、少ない計算コストで多くの(多様な)特徴を学習できるため、高い性能を発揮することが示されました。チャンネルを分けることが、異なる側面に特化したフィルターを学習させる正則化のような効果を持つとも考えられています。
一言でまとめると…
グループ化畳み込みは、チャンネルをいくつかのグループに分割して、それぞれ別々に畳み込みを行うことで、計算コストを抑えつつモデルの表現力を高める手法です。
4. アップサンプリングと逆畳み込み (Transposed Convolution)

1. これは何? 一言でいうと…
通常の畳み込みとは逆に、入力データを拡大してから畳み込みを行うことで、特徴マップのサイズを大きくする処理です。
名前は「逆」ですが、やっていることは「特殊なパディング(0埋め)をしてから、普通の畳み込みを行う」だけです。
2. 何のために使うの? (黄色ハイライト部分)
畳み込み層やプーリング層で圧縮(縮小)した特徴マップを、元の画像サイズに向かって拡大するために使われます。
これは、主に以下のモデルで重要な役割を果たします。
- 生成モデル (GANなど): ノイズから高解像度の画像を生成する過程で、層を経るごとに画像を大きくしていく必要があるため。代表例:DCGAN
- セマンティックセグメンテーション: 画像のピクセル単位でクラス分類を行うため、一度圧縮した特徴マップを元の画像サイズまで復元する必要があるため。FCN, U-Net
- オートエンコーダ: 入力画像を圧縮(エンコード)し、再び元の画像に復元(デコード)する際の、デコーダ部分で使われます。
3. どうやって拡大するの? (図解ステップ)
逆畳み込みの計算は、入力データを**「すき間」を空けて拡大し、適切な量のパディングを施してから、最後にstride=1で通常の畳み込み**を行う、という手順で実現されます。
図の例 (stride=2) を見ると、以下の手順で処理が進んでいます。
-
Step1: ピクセル間に0を追加 (拡大)
stride=2なので、ピクセルとピクセルの間に(2-1)=1個の0を追加し、データをスカスカに広げます。 -
Step2: 周囲に0を追加 (パディング)
計算のつじつまを合わせるため、周囲に適切な数の0を追加します。 -
Step3: (指定されたパディングを調整)
今回はpadding=0なので何もしません。 -
Step4: 通常の畳み込み
Step3で完成した拡大済みマップに対して、**必ずstride=1**で通常の畳み込みを行い、最終的な出力(拡大された特徴マップ)を得ます。
試験当日はこちらの計算の方が楽

この図は「転置畳み込み (Transposed Convolution)」または「逆畳み込み (Deconvolution)」と呼ばれる操作の計算例を示しています。
通常の畳み込みが入力画像を小さくする(または同じサイズに保つ)のに対し、転置畳み込みは入力画像を大きくする(アップサンプリングする)目的で使われます。主に、画像生成モデル(GANなど)のデコーダ部分や、セマンティックセグメンテーションのアップサンプリング層などで利用されます。
転置畳み込みの基本的な考え方
- 入力データの各要素を個別に処理: 入力データ(特徴マップ)の各要素が、それぞれカーネル全体と乗算されます。
- 結果を「広げる」ように配置: 各入力要素とカーネルの乗算結果は、出力特徴マップの対応する位置に「広げられる」ように配置されます。
- 重なり合う部分の加算: 複数の入力要素から生成された部分的な出力マップが重なり合う場合、その重なり合う部分の値は加算されます。
図の具体的な計算手順
入力データ [[2, 2], [1, 1]] とカーネル [[1, 2], [1, 2]] を使って、出力 [[2, 6, 4], [3, 9, 6], [1, 3, 2]] がどのように計算されるかを見ていきましょう。
ここでは、入力データの各要素がカーネルと乗算され、その結果が3x3の出力マップに配置されていく様子を追います。
1. 入力データ (0,0) の 2 の処理
- 入力データの左上
2にカーネル[[1, 2], [1, 2]]を乗算します。
2 * [[1, 2], [1, 2]] = [[2, 4], [2, 4]] - この
2x2の結果を、出力マップの左上(0,0)の位置から配置します。(図の左上の「入力データ」「カーネル」から右の[[2, 4, 0], [2, 4, 0], [0, 0, 0]]2x2の部分に[[2,4],[2,4]]が配置されている部分に相当します。)
2. 入力データ (0,1) の 2 の処理
- 入力データの右上
2にカーネル[[1, 2], [1, 2]]を乗算します。
2 * [[1, 2], [1, 2]] = [[2, 4], [2, 4]] - この
2x2の結果を、出力マップの(0,1)の位置(1つ右にずらした位置)から配置します。(図の右上の「入力データ」「カーネル」から右の[[0, 2, 4], [0, 2, 4], [0, 0, 0]]2x2の部分に[[2,4],[2,4]]が配置されている部分に相当します。)
3. 入力データ (1,0) の 1 の処理
- 入力データの左下
1にカーネル[[1, 2], [1, 2]]を乗算します。
1 * [[1, 2], [1, 2]] = [[1, 2], [1, 2]] - この
2x2の結果を、出力マップの(1,0)の位置(1つ下にずらした位置)から配置します。(図の左下の「入力データ」「カーネル」から右の[[0, 0, 0], [1, 2, 0], [1, 2, 0]]2x2の部分に[[1,2],[1,2]]が配置されている部分に相当します。)
4. 入力データ (1,1) の 1 の処理
- 入力データの右下
1にカーネル[[1, 2], [1, 2]]を乗算します。
1 * [[1, 2], [1, 2]] = [[1, 2], [1, 2]] - この
2x2の結果を、出力マップの(1,1)の位置(1つ右、1つ下にずらした位置)から配置します。(図の右下の「入力データ」「カーネル」から右の[[0, 0, 0], [0, 1, 2], [0, 1, 2]]2x2の部分に[[1,2],[1,2]]が配置されている部分に相当します。)
5. 全ての結果の加算
上記1~4で得られた4つの部分的な出力マップを、要素ごとに加算します。
[[2, 4, 0], [[0, 2, 4], [[0, 0, 0], [[0, 0, 0],
[2, 4, 0], + [0, 2, 4], + [1, 2, 0], + [0, 1, 2],
[0, 0, 0]] [0, 0, 0]] [1, 2, 0]] [0, 1, 2]]
= [[(2+0+0+0), (4+2+0+0), (0+4+0+0)],
[(2+0+1+0), (4+2+2+1), (0+4+0+2)],
[(0+0+1+0), (0+0+2+1), (0+0+0+2)]]
= [[2, 6, 4],
[3, 9, 6],
[1, 3, 2]]
この結果が、図の最終的な「出力」と一致します。
まとめ
転置畳み込みは、このように入力データの各要素がカーネルを「広げる」ように作用し、その結果が重なり合って加算されることで、入力よりも大きな出力サイズを生成します。この例では、ストライド1、パディング0の通常の畳み込みの逆操作に相当する計算が行われています。
注意点: 別名がたくさん!
「逆畳み込み」は非常に多くの別名を持つため混乱しやすいですが、E資格対策としてはこれらが同じものを指すと覚えておくことが重要です。
- Transposed Convolution (転置畳み込み): 最も正式な呼び方。
- Deconvolution (デコンボリューション): よく使われるが、数学的な意味とは異なるため誤解を招きやすい呼び方。
- Fractionally-strided Convolution: 小数ストライドの畳み込み。
一言でまとめると…
逆畳み込みは、「入力データにすき間を開けて拡大し、普通の畳み備みを行うことで、結果的に出力を大きくする」テクニックです。
1. プーリングとは? 一言でいうと…
特徴マップの**サイズを小さくする(ダウンサンプリング)**ための処理です。
近傍のいくつかのピクセルを、1つの代表値に集約します。
主な目的:
- 計算量の削減: データサイズが小さくなるため、後続の層の計算が軽くなります。
- 位置ずれへの耐性向上: 細かい位置の違いを無視して、大局的な特徴を捉えることができます(ロバスト性の向上)。
- 過学習の抑制: 詳細な情報を捨てることで、モデルが些細なノイズに過剰に反応するのを防ぎます。
代表的なプーリング手法
① Max Pooling (最大値プーリング)
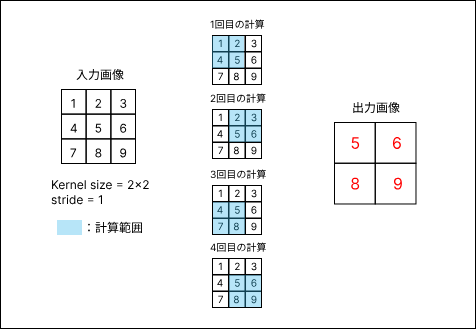
- 処理: 領域内(例: 2x2の範囲)の最大値を代表値として取り出します。
- 特徴: その領域で最も強く反応した特徴を抽出します。エッジなど、際立った特徴を保持するのに長けており、最も広く使われているプーリング手法です。
② Average Pooling (平均値プーリング)
- 処理: 領域内の平均値を代表値として取り出します。
- 特徴: 領域内の特徴を「丸めた」情報を取り出します。Max Poolingほど特徴を先鋭化させず、全体的な傾向を保持します。
③ Lp pooling (Lpプーリング)

- 処理: 領域内の各ピクセル値をp乗して合計し、そのp乗根を取ります。
-
特徴: Max PoolingとAverage Poolingを一般化したものです。
- p=1 のとき → Average Pooling と同じ(ほぼ)。
- p=∞ (無限大) のとき → Max Pooling と同じ。
- pの値を調整することで、2つの中間的な性質を持たせることができます。
④ Global Average Pooling (GAP / 大域的平均プーリング)
- 処理: 各チャンネルの特徴マップ全体から、平均値を1つだけ計算します。
-
特徴:
-
7x7x256のような大きな特徴マップを、一気に1x1x256のベクトルに変換できます。 - これにより、全結合層(Fully Connected Layer)を不要にしたり、そのパラメータ数を大幅に削減できます。過学習を強く抑制する効果があり、現代的なCNN(例: ResNet, GoogLeNet)で分類層の直前によく使われます。
- Global Max Poolingも存在しますが、GAPの方が広く使われます。
-
問題:Depthwise Separable Convolutionの計算量比較
以下の条件で、通常の畳み込みとDepthwise Separable Convolutionの計算量を比較し、Depthwise Separable Convolutionによる計算量削減率を求めなさい。
【条件】
-
入力特徴マップのサイズ:
高さ(H) = 112,幅(W) = 112,チャンネル数(Cin) = 32 -
畳み込みカーネルのサイズ:
高さ(Kh) = 3,幅(Kw) = 3 -
出力チャンネル数(Cout):
64 -
ストライド(S):
1 -
パディング:
same(出力特徴マップのサイズは入力と同じとする)
【計算対象】
- 通常の畳み込みの計算量
- Depthwise Separable Convolutionの計算量
- Depthwise Convolutionの計算量
- Pointwise Convolutionの計算量
- Depthwise Separable Convolution全体の計算量
- Depthwise Separable Convolutionによる計算量削減率(通常の畳み込みと比較して何分の1になるか、または何%削減されるか)
解答
まず、計算に必要な各パラメータを確認します。
-
H_in = 112,W_in = 112,Cin = 32 -
Kh = 3,Kw = 3 Cout = 64-
S = 1,padding = 'same'のため、H_out = H_in = 112,W_out = W_in = 112
1. 通常の畳み込みの計算量
通常の畳み込みでは、Kh x Kw x Cin のカーネルが Cout 個用意され、それぞれが入力特徴マップ全体に適用されます。出力特徴マップの各ピクセルを計算するために必要なMACsは Kh * Kw * Cin です。これが H_out * W_out * Cout 個の出力ピクセルに対して行われます。
計算式: Kh * Kw * Cin * Cout * H_out * W_out
計算:
3 * 3 * 32 * 64 * 112 * 112
= 9 * 32 * 64 * 12544
= 288 * 64 * 12544
= 18432 * 12544
= 231,239,808 MACs
通常の畳み込みの計算量: 231,239,808 MACs
2. Depthwise Separable Convolutionの計算量
Depthwise Separable Convolutionは、Depthwise ConvolutionとPointwise Convolutionの2つのステップに分かれます。
a. Depthwise Convolutionの計算量
Depthwise Convolutionでは、入力チャンネルごとに Kh x Kw x 1 のカーネルが適用されます。Cin 個のカーネルがそれぞれ対応する入力チャンネルに適用され、Cin 個の出力チャンネルを生成します。出力特徴マップの各ピクセルを計算するために必要なMACsは Kh * Kw * 1 です。これが H_out * W_out * Cin 個の出力ピクセルに対して行われます。
計算式: Kh * Kw * 1 * Cin * H_out * W_out
計算:
3 * 3 * 1 * 32 * 112 * 112
= 9 * 32 * 12544
= 288 * 12544
= 3,612,672 MACs
Depthwise Convolutionの計算量: 3,612,672 MACs
b. Pointwise Convolutionの計算量
Pointwise Convolutionでは、Depthwise Convolutionの出力(H_out x W_out x Cin)に対して、1 x 1 x Cin のカーネルが Cout 個適用されます。出力特徴マップの各ピクセルを計算するために必要なMACsは 1 * 1 * Cin です。これが H_out * W_out * Cout 個の出力ピクセルに対して行われます。
計算式: 1 * 1 * Cin * Cout * H_out * W_out
計算:
1 * 1 * 32 * 64 * 112 * 112
= 32 * 64 * 12544
= 2048 * 12544
= 25,699,328 MACs
Pointwise Convolutionの計算量: 25,699,328 MACs
c. Depthwise Separable Convolution全体の計算量
Depthwise ConvolutionとPointwise Convolutionの合計です。
計算:
3,612,672 (Depthwise) + 25,699,328 (Pointwise)
= 29,312,000 MACs
Depthwise Separable Convolution全体の計算量: 29,312,000 MACs
3. Depthwise Separable Convolutionによる計算量削減率
通常の畳み込みの計算量とDepthwise Separable Convolution全体の計算量を比較します。
削減率 (倍率): 通常の畳み込みの計算量 / Depthwise Separable Convolution全体の計算量
= 231,239,808 / 29,312,000
≈ 7.88 倍
削減率 (パーセンテージ): (通常の畳み込みの計算量 - Depthwise Separable Convolution全体の計算量) / 通常の畳み込みの計算量 * 100%
= (231,239,808 - 29,312,000) / 231,239,808 * 100%
= 201,927,808 / 231,239,808 * 100%
≈ 87.3% 削減
まとめ
-
通常の畳み込み計算量:
231,239,808 MACs -
Depthwise Convolution計算量:
3,612,672 MACs -
Pointwise Convolution計算量:
25,699,328 MACs -
Depthwise Separable Convolution全体の計算量:
29,312,000 MACs - 計算量削減率: 通常の畳み込みと比較して 約 7.88 倍 の計算量削減(約 87.3% の計算量削減)
この問題を通して、Depthwise Separable Convolutionがいかに効率的であるか、具体的な数値で理解できたかと思います。E資格の学習、引き続き頑張ってください!