【TypeScript】1%×100回=63%らしいので、コードを書いて検証してみた
検証内容
1%は100回やっても63%しか起こらないらしいです。
具体的に言うと、1%の確率で起こる事象を100回試行したときに1回でも起こる確率は63% です。
と言っても、私のような確率素人にとっては直感的ではない話です。
ネットもChatGPTもそう言ってるので正しいのでしょうが、いまいちピンときません。
ということで、本当なのか検証するためにコードを書きます。
前提知識: 確率の用語集
この記事で頻繁に出てくる用語です。
- 事象(
event): 試行の結果として起こりうる出来事 - 試行(
experiment): ある結果を得るために行う行為や操作 - 確率(
probability): ある事象が起こる可能性の度合い
また、こんな用語もあります。
-
trial: 1回の試行(類義語:experimentは複数回の試行) -
occurredやsuccess: 事象が発生した
解説: 63%の計算方法
先ほど数学的には63%と言いましたが、どうやったら計算できるのか解説しておきます。
ざっくりいうとこんな感じです。
1回でも当たる確率=1-1回も当たらない確率 1回も当たらない確率=1回の試行で当たらない確率^{試行回数} 1回の試行で当たらない確率=1-1回の試行で当たる確率 - 今回の条件の数字を代入すると
1-(1-0.01)^{100}
ということで、
詳しく知りたい方は以下の記事をご覧ください。
検証方法
ということで、さっそく検証を始めます。
前述の内容をプログラミングで実際にやってみて、だいたい63%になれば正しいと言えます。
なお、コードはTypeScriptで書いてBunで実行します。
要件
今回やる必要があることは、主に以下の2点です。
- 1%で起こる事象を100回試行し、事象が起こったかどうか判定する
- ↑を十分な回数試行し、事象が起こった割合を求める
具体的な試行回数やパフォーマンスは決めず、雰囲気でやります。
コード
ということで、私が書いてChatGPTが監修したコードがこちらです。
interface TrialResult {
occurred: boolean; // 事象が発生したか
attemptNumber: number; // 何回目で発生したか(デバッグや検証用)
}
// 1%の確率の事象を最大100回まで繰り返し試行し、発生すれば即終了
function runSingleTrial(): TrialResult {
for (let i = 0; i < 100; i++) {
const occurred = Math.floor(Math.random() * 100) === 0;
if (occurred) return { occurred: true, attemptNumber: i + 1 };
}
return { occurred: false, attemptNumber: -1 };
}
// 指定回数だけ runSingleTrial を実行し、発生率を求める
function runExperiment(trialCount: number) {
const results = Array.from({ length: trialCount }, runSingleTrial);
const successCount = results.filter(result => result.occurred).length;
const probability = successCount / trialCount;
return { probability, results };
}
const TRIALS = 100000;
const { probability } = runExperiment(TRIALS);
console.log(`発生確率: ${(probability * 100).toFixed(2)}%(試行回数: ${TRIALS})`);
やってることはこんな感じです。
-
runSingleTrialは100回試行した結果1%で起こる事象が起こったかどうかを返す -
runExperimentはrunSingleTrialをtrialCount引数で指定された試行回数実行する -
runExperimentはrunSingleTrialの呼び出し結果たちの中で何回事象が起こったかを返す - あとは
TRIALS定数で試行回数を決め、runExperimentを呼び出すだけ
なお、頭の中だけで理解しようとするとこんがらがりやすいです。
実際にTypeScript Playgroundなどで動かしてみるとわかりやすいかもしれません。
おまけ: Scalaはいいぞ
私が密かに好きな言語であるScalaでも書いてみたので載せておきます。
やってることはTypeScriptとだいたい同じで、もちろん結果も同じです。
case class TrialResult(occurred: Boolean, attemptNumber: Int)
def randomEvent: Boolean = {
import scala.util.Random
Random.nextInt(100) == 1
}
def runSingleTrial: TrialResult = {
val list = LazyList.continually(randomEvent).take(100)
TrialResult(
occurred = list.exists(identity),
attemptNumber = list.indexWhere(identity)
)
}
def runExperiment(trials: Int): Float = {
val list = LazyList.continually(runSingleTrial).take(trials)
list.count(_.occurred).toFloat / trials
}
val TRIALS = 100000
val probability = runExperiment(TRIALS)
println(s"確率: ${probability * 100}% (試行回数: $TRIALS 回)")
実行環境はScastieというプレイグラウンドです。
Scalaは書いていて非常に楽しかったです。
特にrunSingleTrialとrunExperimentの1行目はかなり気持ちよく実装できました。
Scalaの発展のためにも、ぜひ充実した公式ツアーを覗いてみてください。
実行方法
あとはこのコードをBunで実行するだけです。
ですが、1回だけの実行ではブレが出そうで不安なので、念の為複数回実行します。
発生確率: xx% (試行回数: xxxxxx)
発生確率: xx% (試行回数: xxxxxx)
発生確率: xx% (試行回数: xxxxxx)
...
結果
さっそく結果を見てみます。
前述の通りに実行すると、結果はだいたい以下のようになるはずです。
確率: 63.432100000000005% (試行回数: 1000000)
確率: 63.370099999999994% (試行回数: 1000000)
確率: 63.363400000000006% (試行回数: 1000000)
確率: 63.3876% (試行回数: 1000000)
確率: 63.3809% (試行回数: 1000000)
...
63%で安定しているので、コードの実行結果は63%になります。
数学的な計算でも63%くらいになるということで、この結果はある意味想定通りです。
以上の検証から、「1%で起こる事象を100回試行したときに事象が起こる確率は63%になる現象は正しい」と言えます。
素人の直感的には100%と言いたくなりますが、やはり直感より数学のほうが正しかったようです。
ということで、検証はこれで終わりになります。
似た題材には他にもモンティ・ホール問題などがあるので、よければあなたも検証してみてください。
おまけ: 自然対数eとの関係性
さて、この記事では「1%を100回」で検証しましたが、ここまで来たら「10%を10回」や「0.1%を1000回」も気になってくるところです。
しかしこの記事のような検証では精度が不安なので、ここはおとなしく計算式で求めます。
求めたものがこちらです。
- 10%が10回で引ける確率:
0.6513\ldots 1-0.9^{10} - 1%が10回で引ける確率:
0.6339\ldots 1 - 0.99^{100} - 0.1%が1000回で引ける確率:
0.6323\ldots 1 - 0.999^{1000} - 0.01%が10000回で引ける確率:
0.6321\ldots 1 - 0.9999^{10000}
計算式で求める方法
ということで、この式の作り方を解説します。
検証内容でも触れましたが、
注目すべきは
では、
これは結構簡単で、先ほどの式を応用すると
ここまで出てきたような「
そして、このような確率
n e
話は変わりますが、上の式の
なんと、
なお、
これは何故かを知るためには、まず
そして
これと似たような式をどこかで見たことがないでしょうか。
そう、先ほどの
つまり、
この式をグラフにすると、だいたいこんな感じになります。
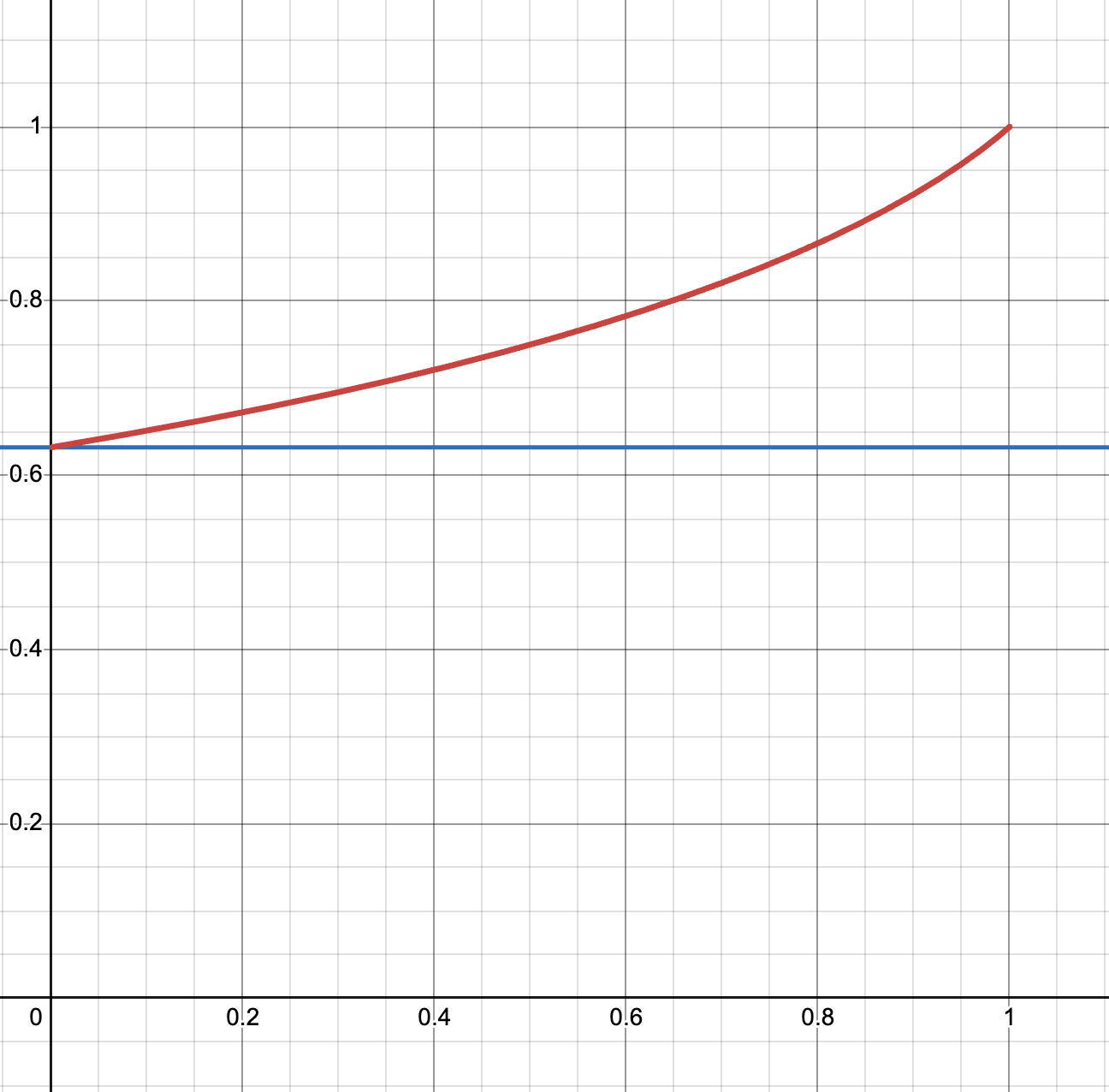
-
x \frac{1}{n} -
y n
また、
- 赤線はさっきの式(
1-(1-\frac{1}{n})^n - 青線は
1-\frac{1}{e}=0.632...
です。
グラフの書き方について
グラフはDesmosで書きました。また、その際使った式はこちらです。
- 赤線:
f\left(n\right)=1-\left(1-n\right)^{\frac{1}{n}}\left\{0.001<n<1\right\} - 青線:
y=1-\frac{1}{e}
赤線の式が少し違うのは、先程の式の
グラフの
と言ってもいきなり読み解くのはハードルが高いので、いくつかわかりやすい例を上げます。
- 右上
(1, 1) 100 1 1 100 -
(0.5, 0.75) 50 2 0.75 -
(0.1, 0.651...) 10 10 0.651...
そして、このグラフでは赤線と青線が
こうして見ると、
終わりに
思いがけないところから
最後はChatGPTの言葉を引用して締めたいと思います。
こうした例は、プログラマやデータサイエンティスト、数学を使う人のあいだでは常識に近いです。
もっと数学をがんばろうと思いました。
Discussion