Zenn
Closed5

サーミスタと555を使った温度測定回路の計算式

hardware
七瀬七瀬

以下、特段の注意書きがなければ温度はケルビン (K) を表すものとする。

サーミスタは温度が低いと抵抗値が上がり、高いと抵抗値は下がる。温度により変化するサーミスタの抵抗値の変化の割合を表す物性値は B定数 と呼ばれる。とある温度 T [K] のときの抵抗値が R [Ω] であったとすると、2つの温度と抵抗値を使ってB定数は以下のように定義される。

B := \frac{\ln{R_a} - \ln{R_b}}{\frac{1}{T_a}-\frac{1}{T_b}} \qquad\text{(1)}

実際の製品ではB定数を示す際に2点の温度が明示されていることがあり、その場合は B_{T_a/T_b} のように表記される。ただしこの表記上の温度 T_a, T_b はケルビンではなくセルシウス温度 (℃) で表記されていることが多い。

たとえば 103JT というサーミスタはデータシート上では B_{25/85} = 3435\pm 1\% [K] と表記されている。抵抗-温度特性をもとに再計算すると、

\begin{aligned} R_{25} &= 10000 \\ R_{85} &= 1451 \\ B_{25/85} &= \frac{\ln{10000} - \ln{1451}}{\frac{1}{25 + 273.15}-\frac{1}{85 + 273.15}} \\ &= 3435.426... \end{aligned}

とデータシートの記載と同じB定数が求められる。

ある温度 T_x におけるサーミスタの抵抗値 R_x を求めるには、式 (1) を変形して、

R_x = R_a e^{B\left(\frac{1}{T_x} - \frac{1}{T_a}\right)}

となり、あるサーミスタの抵抗値が R_x であったときの温度 T_x は、

T_x = \left(\frac{1}{B}\ln\frac{R_x}{R_a}+\frac{1}{T_a}\right)^{-1} \qquad\text{(2)}

となる。

七瀬七瀬

サーミスタと555を使った下記の回路について考える。

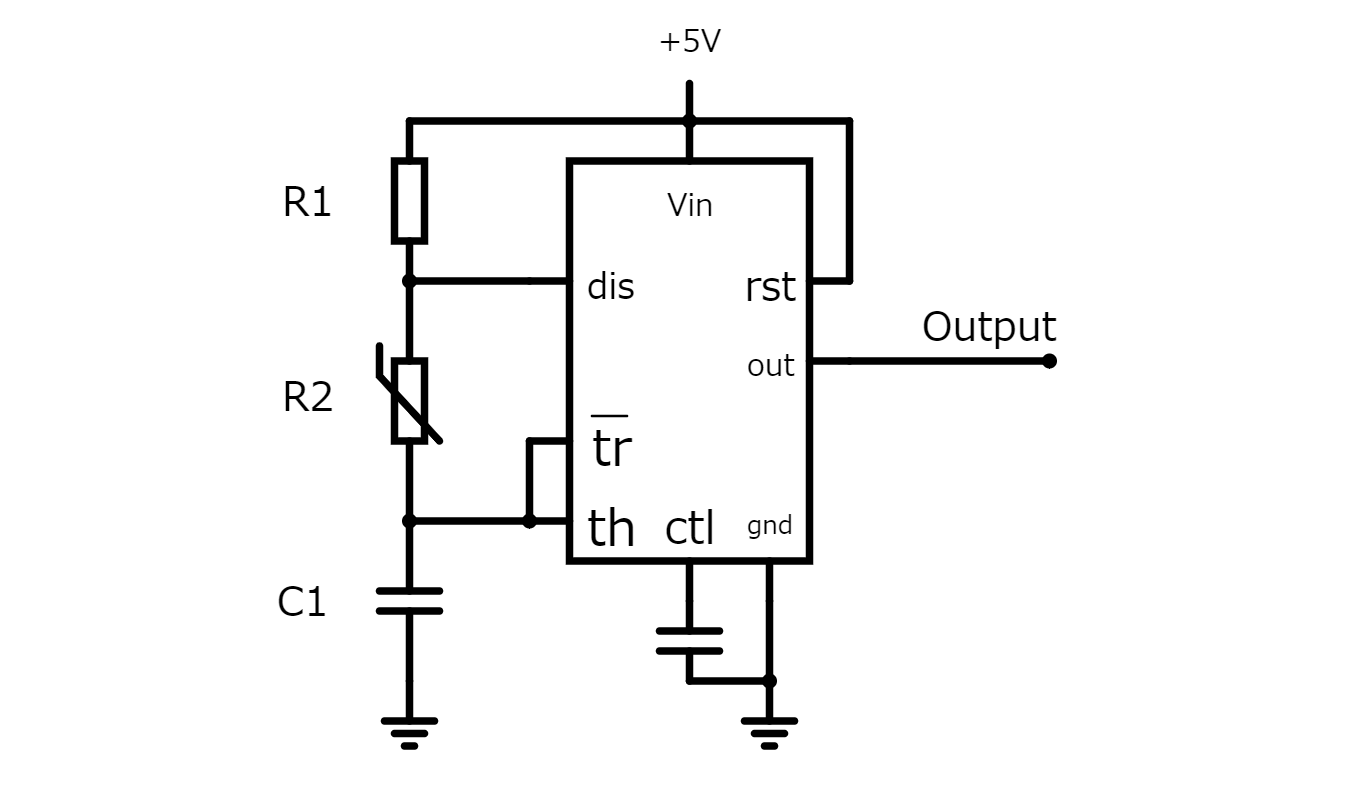
このとき、抵抗器の抵抗値を R_1 [Ω]、サーミスタの抵抗値を R_2 [Ω]、コンデンサの静電容量を C_1 [F] とすると出力される矩形波の周波数 f [Hz] は

f = \frac{\frac{1}{\ln2}}{(R_1+2R_2)C_1} \qquad\text{(3)}

となる。ところで、\frac{1}{\ln2} はしばしば 1.44 という数値で計算される。555の個体差によってこれ未満の数値は無視できるために省略されているようである。計算の便宜上、ここでは省略せずに元の数値のまま使う。

式 (3) をサーミスタの抵抗値 R_2 について解くと、

R_2 = \frac{\frac{1}{\ln2}}{2fC_1}-\frac{R_1}{2} \qquad\text{(4)}

となる。

七瀬七瀬

R_x = R_2 として式 (2) へ式 (4) を代入すると、

\begin{aligned} T(f) &= \left(\frac{1}{B}\ln\frac{\frac{\frac{1}{\ln2}}{2fC_1}-\frac{R_1}{2}}{R_a}+\frac{1}{T_a}\right)^{-1} \\ &= \frac{BT_a}{T_a \ln\frac{\frac{\frac{1}{\ln2}}{2fC_1}-\frac{R_1}{2}}{R_a}+B} \qquad\text{(5)} \end{aligned}

となる。これにより周波数 f から温度 T を求めることができる。一見複雑な式だが、B, R_a, R_1, C_1, T_a が変化しない定数だと考えられることから

\begin{aligned} \alpha &= -\ln2-\ln{R_a} \\ E &= \frac{1}{\ln2} \end{aligned}

と置けば、式 (5) は

\begin{aligned} T(f) &= \frac{BT_a}{T_a \left(\ln \left(\frac{E}{fC_1}-R_1 \right)+\alpha \right)+B} \qquad\text{(6)} \end{aligned}

とより簡単に表記できる。

七瀬七瀬

JavaScriptでこの計算を実装すると以下のようになる。ただし入力と出力の温度はセルシウス温度 (℃) である。

const K = 273.15;

function B(ta, ra, tb, rb) {
  return (Math.log(ra) - Math.log(rb)) / (1 / (ta + K) - 1 / (tb + K));
}

function T(f, ta, ra, tb, rb, c1, r1) {
  const b_const = B(ta, ra, tb, rb);
  const alpha = -Math.log(2) - Math.log(ra);
  return (b_const * (ta + K)) / ((ta + K) * (Math.log(Math.LOG2E / (f * c1) - r1) + alpha) + b_const) - K;
}

T_a, R_a, T_b, R_b はデータシートに記載の値、C_1, R_1 をそれぞれ 0.1 [μF]、1 [kΩ] とし、周波数を 1 [kHz] と指定すると、求めたい温度は

> T(1e3, 25, 10e3, 85, 1.451e3, 0.1e-6, 1e3)
< 35.679906541566424

と計算できる。

このスクラップは2022/11/12にクローズされました