ネットワーク分析の雰囲気をつかむ

はじめに

この記事は筆者の現状の理解に基づいたネットワーク分析のチュートリアルです。タイトルにもあるように、分析の雰囲気を掴むことを目的としているため、PythonのコードをJupyter Notebookで実行しながら初歩的な分析を一通り体験する形をとっています。詳しく知りたくなった方向けに、最後にネットワーク科学のテキストや関連する記事、データセットなどをまとめています。
本チュートリアルがネットワーク分析、そしてその理論的背景にあたるネットワーク科学に興味を持つきっかけとなれば嬉しいです。

世の中至る所にネットワーク

ネットワークとは、頂点（ノード）が枝（辺、リンク、エッジ）で結ばれたものです。何を頂点や枝とみなすかによって、さまざまな対象をネットワークとして表現できます。その柔軟性ゆえに私たちの住む世界には、至る所にネットワークが潜んでいると言えるでしょう。例えば、遺伝子の制御関係や脳内神経細胞の情報伝達関係、生態系における「食う/食われる」の関係、人間社会の交友関係やビジネスにおける取引関係、国際貿易関係、交通網や電力網、インターネットなどたくさんの例を挙げることができます。このように、対象を頂点と枝のつながりとして抽象化することで、生命現象から社会・経済現象に至るまで様々な領域にネットワークを見出せます。

とはいえ、対象が違えばシステムを構成する要素（細胞、人間、企業、etc.）が異なるわけで、個々のネットワークは異なる構造を持っているのではないかと思えます。ところが、現実の多くのネットワークの構造には共通の性質が見られることが1990年代の終わり頃から多くの研究を通してわかってきました。代表的なものは、「スケールフリー性」や「スモールワールド性」といった性質です。これらの研究成果の蓄積によって、今日「ネットワーク科学」と総称される学問分野が成立しています。

ネットワーク科学自体の知見も面白いのですが、ここでは深く立ち入らずに、手を動かしながらネットワーク分析がどのようなものか見ていきましょう。

【実践】ネットワーク分析

ネットワーク分析の例として、社会ネットワークとして有名なZacharyの空手クラブの交友関係のネットワークを分析します。このネットワークでは、クラブ活動以外でも定期的に交流していたメンバーの間にエッジが張られています。

ネットワーク分析を行うソフトは色々ありますが、ここではNetworkXを用いて分析します。

# 必要なパッケージを読み込む
import networkx as nx
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

NetworkXのバージョンはv3.1です。

nx.__version__
# '3.1'

分析の流れ

• ネットワークの取得と規模の確認
• ネットワークの可視化
• 次数分布の確認
• 中心性の計算
• コミュニティの確認

ネットワークの取得と規模の確認

まずは、分析するネットワークを取得します。

# 空手クラブのネットワークを取得
G = nx.karate_club_graph()

ネットワークデータを取得したら、自分が調べようとしている対象がどれほどの規模のネットワークなのかを確認します。空手クラブネットワークのノード数とエッジ数を見てみましょう。

## ノード数とエッジ数
N = nx.number_of_nodes(G)
M = nx.number_of_edges(G)
df = pd.DataFrame({"#nodes": [N], "#edges": [M]})
df

	#nodes	#edges
0	34	78

ネットワークの可視化

34個のノードからなるネットワークであることがわかりました。次にどういう形のネットワークなのかを視覚的に確認します。

NetworkXは可視化に不向きですが、小規模のネットワークであればあまり問題ないと思います。大規模なネットワークを可視化したい場合は、graph-tool をお勧めします。

# レイアウトの取得
pos = nx.spring_layout(G)
# 描画
fig, ax = plt.subplots(figsize=(5,3))
nx.draw(G, pos=pos, node_size=100, node_color="teal", width=0.4, ax=ax)
fig.tight_layout()

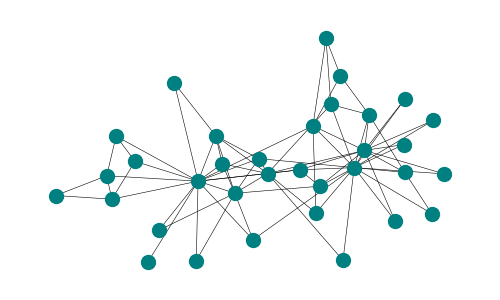
ネットワークによっては描画するだけで特徴（e.g., ハブやコミュニティの存在）がわかることがあります。ネットワークを描いてみて全体の大雑把な様子が掴めたら、ネットワークの特徴量を調べていきます。

次数分布の確認

ネットワークの代表的な特徴量は次数(degree)です。次数とはノードが持つ枝の数で、NetworkXの関数を使えば個々のノードの次数を全て列挙することができます。

# 次数列の取得
degree = dict(nx.degree(G)).values()
# データフレーム化
df_degree = pd.DataFrame({"degree": degree})
df_degree.T

index	0	1	2	3	4	5	6	7	8	9	...	28	29	30	31	32	33
degree	16	9	10	6	3	4	4	4	5	2	...	3	4	4	6	12	17

次数の要約統計量は次のとおりです。

# 要約統計量
df_degree.describe().T

	count	mean	std	min	25%	50%	75%	max
degree	34.0	4.588235	3.877813	1.0	2.0	3.0	5.0	17.0

数字の羅列を見てもデータの特徴はよくわからないため、データの分布を確認してみましょう。これを次数分布(degree distribution)といい、ネットワーク分析においてネットワークの構造を調べるには次数分布を調べるのが定石です。

## 次数分布（ヒストグラム）の描画
# ヒストグラムの描画
fig, ax = plt.subplots(figsize=(4,3))
ax.hist(x="degree", data=df_degree, bins=20, color="teal", ec="white")
ax.set_xlabel("Degree", fontsize=15)
ax.set_ylabel("# nodes", fontsize=15)
fig.tight_layout()

次数分布を見てみると、ほとんどのノードは次数が4以下であるのに対して、2つのノードは次数が16と17と大きな値を取っていることがわかります。つまり、この空手クラブのほとんどの部員にとって、クラブ活動以外の場所で交流するほど仲の良いメンバーは2人から4人であった一方、メンバーの半数と親密な交友関係を築いていた部員が2人はいたということです。実は、この2人は部長とインストラクターで、当時の空手クラブではレッスン料の値上げをめぐって部長とインストラクターが対立し、それを機に部員は部長派とインストラクター派に分かれていました[Zachary (1977)]。交友関係の多さ（次数の大きさ）を考慮して再度ネットワークを描画してみると、なんとなくメンバーが二つの人物の周りに集中している様子が伺えます。

# ノードの大きさの調整
node_size = [d*15 for d in degree]
# 描画
fig, ax = plt.subplots(figsize=(5,3))
nx.draw(G, pos=pos, node_size=node_size, node_color="teal", width=0.4, ax=ax)
fig.tight_layout()

ここで注目すべきは、交友関係をネットワークとして表現した時点で、個々人の個性を捨象しているのにも関わらず、ネットワークの構造にそれが現れている点です。ネットワークの構造、すなわち人のつながり方に注目するだけで、誰が中心的な役割を担っているのかを判断できるわけです。

中心性の計算

ネットワーク分析において、このようにどのノードが重要であるかを知りたいことは多々あります。例えば、SNSにおけるインフルエンサーやサプライチェーンにおけるキープレイヤーの特定などが挙げられます。小規模なネットワークであれば、ネットワークを可視化して視認することもできなくはないですが、やはりピンポイントに個々のノードの中心性を表す指標があれば便利です。実際、さまざまな中心性の指標が考えられています。

本記事の目的はネットワーク分析の雰囲気を掴むことなので、ここでは各中心性指標の定義には触れません。ですが、実際の分析ではそれぞれの特徴を理解した上で使用するべきだと思います。詳しく知りたい方は、村田(2019)やNewman(2018)を参照してください。

（2023年9月8日追記）
現在ネットワークの中心性に関する連載を作成しています．次数中心性からPageRankまでを扱う予定です．※媒介中心性と近接中心性については未定
https://zenn.dev/nagayu71/articles/a2c5b290e8b11e

## 各種中心性の計算
# 次数中心性
degree_centrality = nx.degree_centrality(G)
# 固有ベクトル中心性
eigenvector = nx.eigenvector_centrality(G)
# カッツ中心性
Katz = nx.katz_centrality(G)
# PageRank
PageRank = nx.pagerank(G)
# 媒介中心性
betweenness = nx.communicability_betweenness_centrality(G)
# 近接中心性
closeness = nx.closeness_centrality(G)

# データフレームにまとめる
df_centrality = pd.DataFrame(
    {"DC": degree_centrality,
     "EV": eigenvector,
     "Katz": Katz,
     "PR": PageRank,
     "BTW": betweenness,
     "CLN": closeness})
df_centrality.round(2).head()

index	DC	EV	Katz	PR	BTW	CLN
0	0.48	0.36	0.32	0.09	0.6	0.57
1	0.27	0.27	0.24	0.06	0.29	0.49
2	0.3	0.32	0.27	0.06	0.4	0.56
3	0.18	0.21	0.19	0.04	0.18	0.46
4	0.09	0.08	0.12	0.02	0.05	0.38

要約統計量も見てみましょう。

index	DC	EV	Katz	PR	BTW	CLN
count	34.0	34.0	34.0	34.0	34.0	34.0
mean	0.14	0.15	0.16	0.03	0.13	0.43
std	0.12	0.09	0.06	0.02	0.15	0.07
min	0.03	0.02	0.09	0.01	0.01	0.28
25%	0.06	0.08	0.12	0.01	0.04	0.37
50%	0.09	0.1	0.13	0.02	0.08	0.38
75%	0.15	0.19	0.19	0.03	0.17	0.48
max	0.52	0.37	0.33	0.1	0.6	0.57

計算した中心性が反映される形で再度ネットワークを可視化します。同じ作業を繰り返すことになるので、可視化用の関数を作っておきます。

# 描画用の関数
def draw_network_with_centralities(G, pos, centralities, centrality_name, ax, node_size_multiple=1500):
    # 中心性に基づいてノードのサイズを計算
    max_centrality = max(centralities.values())
    node_sizes = [node_size_multiple * v for v in centralities.values()]

    # 中心性に基づいてノードの色を計算
    colormap = plt.cm.spring  # カラーマップを指定
    node_colors = [colormap(v / max_centrality) for v in centralities.values()]

    # グラフを描画
    nx.draw_networkx(G, pos, with_labels=True, node_size=node_sizes, node_color=node_colors, font_color='black', width=0.4, alpha=0.9, font_size=10, ax=ax)

    # カラーバーを追加
    sm = plt.cm.ScalarMappable(cmap=colormap, norm=plt.Normalize(vmin=0, vmax=max_centrality))
    sm.set_array(np.array(list(centralities.values())))  # 中心性の値の配列を設定
    plt.colorbar(sm, ax=ax)
    ax.set_title(centrality_name)

中心性ごとに可視化すると長くなるので、ここではまとめて表示します。

# 描画のキャンパスを用意
fig = plt.figure(figsize=(5*4,3*3))
# 軸を2行3列で追加
ax1 = fig.add_subplot(2, 3, 1)  # 1行目の左から1番目
ax2 = fig.add_subplot(2, 3, 2)  # 1行目の左から2番目
ax3 = fig.add_subplot(2, 3, 3)  # 1行目の左から3番目
ax4 = fig.add_subplot(2, 3, 4)  # 2行目の左から1番目
ax5 = fig.add_subplot(2, 3, 5)  # 2行目の左から2番目
ax6 = fig.add_subplot(2, 3, 6)  # 2行目の左から3番目

# 次数中心性
draw_network_with_centralities(G, pos, degree_centrality, "Degree Centrality",ax=ax1)
# 固有ベクトル中心性
draw_network_with_centralities(G, pos, eigenvector, "Eigenvector Centrality", ax=ax2)
# カッツ中心性
draw_network_with_centralities(G, pos, Katz, "Katz Centrality", ax=ax3)
# PageRank
draw_network_with_centralities(G, pos, PageRank, "PageRank", ax=ax4, node_size_multiple=6000)
# 媒介中心性
draw_network_with_centralities(G, pos, betweenness, "Betweenness Centrality", ax=ax5)
# 近接中心性
draw_network_with_centralities(G, pos, closeness, "Closeness Centrality", ax=ax6, node_size_multiple=1000)
fig.tight_layout()

鮮やかな黄色であるほど中心性のスコアは高いので、どの指標で見ても0番と33番のノードの中心性が高いことがわかります。実際、0番はインストラクターで33番は部長です。また、中心性指標によって、中心性の分布は違っているように思えます。中心性のヒストグラムを描いて確かめてみましょう。ここでも繰り返しの操作が発生するので、描画用の関数を準備します。

# 中心性のヒストグラムを描画する関数
def plot_hist(data, x, centrality_name, ax):
  ax.hist(x=x, data=data, bins=20, color="#69b3a2", ec="white")
  ax.set_xlabel(centrality_name, fontsize=10)
  ax.set_ylabel("# nodes", fontsize=10);

# ヒストグラムの描画
# 描画のキャンパスを用意
fig = plt.figure(figsize=(4*3,3*2))
# 軸を2行3列で追加
ax1 = fig.add_subplot(2, 3, 1)  # 1行目の左から1番目
ax2 = fig.add_subplot(2, 3, 2)  # 1行目の左から2番目
ax3 = fig.add_subplot(2, 3, 3)  # 1行目の左から3番目
ax4 = fig.add_subplot(2, 3, 4)  # 2行目の左から1番目
ax5 = fig.add_subplot(2, 3, 5)  # 2行目の左から2番目
ax6 = fig.add_subplot(2, 3, 6)  # 2行目の左から3番目

plot_hist(data=df_centrality, x="DC",  centrality_name="Degree Centrality", ax=ax1)
plot_hist(data=df_centrality, x="EV", centrality_name="Eigenvector Centrality", ax=ax2)
plot_hist(data=df_centrality, x="Katz", centrality_name="Katz Centrality", ax=ax3)
plot_hist(data=df_centrality, x="PR",  centrality_name="PageRank", ax=ax4)
plot_hist(data=df_centrality, x="BTW",  centrality_name="Betweenness Centrality", ax=ax5)
plot_hist(data=df_centrality, x="CLN",  centrality_name="Closeness Centrality", ax=ax6)
fig.tight_layout()

中心性指標によって分布は確かに異なっています。これはそれぞれ定義の仕方が異なるからですが、詳しく知りたい方は村田(2019)やNewman(2018)を参照してください。

コミュニティの確認

先ほど可視化したネットワークですが、よく見るとなんとなく2つのグループに分かれているように思えます。実際、当時の空手クラブでは部長派とインストラクター派で派閥が形成されていたのでした。

このように現実のネットワークでは、ノードが他の場所と比べて密につながった部分が存在し、これをコミュニティと呼びます。なんらかのネットワークデータを手にした時、コミュニティ構造を検出することができれば便利です。例えば、SNS上で嗜好の似た友人を推薦したり、ネットワーク上のコミュニティが特定の性質に与える影響を調べたりと、応用面での可能性が広がります。

ここではGivan-Newman法という方法で、空手クラブのコミュニティを検出してみましょう。

# コミュニティ検出
communities = nx.community.girvan_newman(G)
first_level_communities = next(communities) # 一番上の階層を採用
first_level_communities

# 出力
({0, 1, 3, 4, 5, 6, 7, 10, 11, 12, 13, 16, 17, 19, 21},
 {2, 8, 9, 14, 15, 18, 20, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33})

ネットワーク内のノードが2つのグループに分類されました。これを用いてコミュニティごとに異なる色を割り当ててネットワークを可視化します。

# 各コミュニティに色を割り当てる
colors = ["orangered","deepskyblue"] # 使用したい色
community_colors = dict() # ノードの色を格納する辞書

for i, community in enumerate(first_level_communities):
    for node in list(community):
      community_colors[node] = colors[i]

# ネットワークを描画
node_colors = [community_colors[n] for n in G.nodes()] # ノードの並び順ごとに色を並び替える
fig, ax = plt.subplots(figsize=(5,3))
nx.draw(G, pos, with_labels=True, node_color=node_colors, width=0.4, node_size=150, font_size=10, ax=ax)
fig.tight_layout()

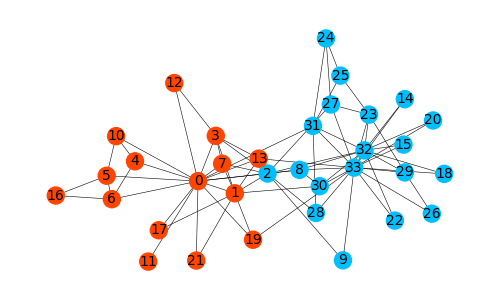
分割結果を見ると、良い感じに2つのコミュニティが検出されている気がしますが、一般にコミュニティ検出アルゴリズムによる分割結果が正しいかどうかを決めるのは難しいです。しかし、この空手クラブのデータに限って言えば、レッスン料をめぐる部長とインストラクターの対立が発展し、クラブが2つに分裂してしまったため、分裂後のグループを真のコミュニティとして比較することができます。networkx.karate_club_graph()には、各ノードにラベルにOfficer（部長）とMr.Hi（インストラクター）が付与されているので、実際の所属グループを簡単に調べることができます。

# 分裂後のグループを取得
officer_side = [n for n, d in G.nodes(data=True) if d["club"] == "Officer"]
instructor_side = [n for n, d in G.nodes(data=True) if d["club"] == "Mr. Hi"]

# グループに色を割り当てる
colors = ["orangered","deepskyblue"] # 使用したい色
group_colors = dict() # ノードの色を格納する辞書

# 部長派: 青, インストラクター派: オレンジ
for n in officer_side:
  group_colors[n] = colors[1]
  for n in instructor_side:
    group_colors[n] = colors[0]

# ネットワークを描画
n_colors = [community_colors[n] for n in G.nodes()]
fig, ax = plt.subplots(figsize=(5,3))
nx.draw(G, pos, with_labels=True, node_color=n_colors, width=0.4, node_size=150, font_size=10, ax=ax)
fig.tight_layout()

instructor_sideの中身は[0, 1, 2, 3, 4, 5, 6, 7, 8, 10, 11, 12, 13, 16, 17, 19, 21]なので、オレンジ色のノードがインストラクター派、青色のノードが部長派としてその後分裂したグループだったということです。先ほどのアルゴリズムによる分割結果と比べると、ほとんど一致していることが確かめられます。この結果が示唆するのは、人と人のつながり（ネットワーク）という情報だけを用いて、新たな社会グループが形成されるという将来の事象を予測しているということです。Zacharyの空手クラブのネットワーク分析は、構成要素のつながり方（構造）が全体として現れる現象を決定するというネットワーク科学の考え方が現れている分析例だと個人的には思います。余談ですが、Zacharyの空手クラブのデータは、分裂前のネットワークの構造だけから2つのコミュニティを推論できるかという観点で分割アルゴリズムをテストする際にしばしば用いられています。

おわりに

この記事ではZacharyの空手クラブのデータを分析して、次数分布、中心性、コミュニティ構造という基本的なネットワークの特徴を確認しました。最初に述べたように、これはネットワーク分析の初歩であり、ネットワーク科学を学べばもっと深くて面白い知見を知ることができます。たとえば、冒頭に挙げた「スモールワールド性」は、どうして世界は狭いと感じるのかという疑問に答えるものになっています。

最後にネットワーク科学をもっと知りたい方向けに、代表的なテキストとネットワーク分析用のツール、ネットワークのデータセットをまとめておきます。

ネットワーク科学の入門テキスト

• Barabási, A.-L.（2019）『ネットワーク科学』池田裕一・井上寛康・谷澤俊弘監訳、京都大学ネットワーク社会研究会訳、共立出版、（英語版）http://networksciencebook.com/
• 村田剛志（2019）『Pythonで学ぶネットワーク分析：ColaboratoryとNetworkXを使った実践入門』オーム社
• 『経済セミナー「特集 ネットワーク科学と経済学」』日本評論社、2020年12月・2021年1月号（経済セミナー編集部note）
• Menczer, F., Fortunato, S. & Davis, C. A. A First Course in Network Science (Cambridge University Press, 2020). URL https://cambridgeuniversitypress.github.io/FirstCourseNetworkScience/.

ネットワーク科学関連の読み物・記事

• マシュー・O・ジャクソン（2020）依田光江訳『ヒューマン・ネットワーク　人づきあいの経済学』、早川書房
• How Network Math Can Help You Make Friends | Quanta Magazine
• Who Is the Most Important Character in Frozen? What Networks Can Tell Us About the World | Frontiers for Young Minds

ネットワーク分析ツール（Python）

• NetworkX
• igraph
• graph-tool

データセット

• Netzschleuder: the network catalogue, repository and centrifuge
• The Colorado Index of Complex Networks
• Stanford Large Network Dataset Collection

参考文献

• Newman, M. (2018). Networks. Oxford university press.
• Zachary, W. W. (1977). An information flow model for conflict and fission in small groups. Journal of anthropological research, 33(4), 452-473.