🎰
ゼロから作るDeepLearning4をRustで書きながらさっくり学んでいく[1章]
はじめに
2022年4月6日にO'reilly Japanより「ゼロから作るDeepLearning4強化学習編」が発売されました。
そこで人気シリーズの第4段のこの本をRustで再実装しながら読み進めていきます。こまかい内容はぜひ購入して確認してください。
1章: バンディット問題
エージェントと環境が相互作用しながらデータを集めながら報酬を得る方法を学習する強化学習。その強化学習の中で最もシンプル、簡単な具体例であるバンディット問題を解くことで、強化学習の特徴を学んでいきます。
バンディット問題
バンディット問題とは、バンディットというある確率でコインを排出する複数のマシンにおいて、どのマシンをプレイすることが最もコインを多く獲得できるのかを探る問題のことです。今回は一定の確率でコインを1枚だけ排出するマシンが複数並んでいることとします。
バンディットアルゴリズムの実装
今回バンディット問題を解くためのアルゴリズム、バンディットアルゴリズムを実装していきます。実装するstructは大きく分けて2つ、バンディットマシン(環境)であるBanditとプレイヤーであるAgentです。
使用するクレート
struct Banditの実装
今回はコインを排出する確率がそれぞれ乱数によって決定する10台のマシンを想定します。このstructでは事前に乱数によって設定された各スロットの排出率rateとスロットをプレイした際に生成した乱数を比較しプレイした際の乱数が大きければ1を、そうでない場合は0を返すものです。
ch01/src/bandit.rs
use rand::Rng;
pub struct Bandit {
pub arms: usize,
pub rates: Vec<f64>,
}
impl Bandit {
pub fn play(&mut self, arm: usize) -> i32 {
let rate: f64 = self.rates[arm];
let random_num: f64 = rand::thread_rng().gen();
if random_num < rate {
1
} else {
0
}
}
}
struct Agentの実装
以下の3種類の変数を有したstruct Agentを実装します。
Qs: 各マシンの価値の推定値を格納する1次元x10の配列(0で初期化)
ns: 各マシンをプレイした回数を格納する1次元x10の配列(0で初期化)
epsilon: ε-greedy法に則ってランダムなプレイを行う確率を格納する変数
ch01/src/bandit.rs
use rand::Rng;
use std::cmp::Ordering;
pub struct Agent {
pub epsilon: f64,
pub Qs: Vec<f64>,
pub ns: Vec<f64>,
}
impl Agent {
pub fn update(&mut self, action: usize, reward: i32) {
self.ns[action] += 1_f64;
self.Qs[action] += (reward as f64 - self.Qs[action]) / self.ns[action];
}
pub fn get_action(&self) -> usize {
let random_num: f64 = rand::thread_rng().gen();
if random_num < self.epsilon {
rand::thread_rng().gen_range(0..self.Qs.len()) as usize
} else {
// return self.Qs.argmax()
self.Qs
.iter()
.enumerate()
.max_by(|(_, a), (_, b)| a.partial_cmp(b).unwrap_or(Ordering::Equal))
.map(|(index, _)| index)
.unwrap() as usize
}
}
}
実行&描画を行うmain関数の実装
ch01/src/bandit.rs
use plotters::prelude::*;
fn main() -> Result<(), Box<dyn std::error::Error>> {
let steps = 1_000;
let epsilon = 0.1;
let mut bandit = Bandit {
arms: 10,
rates: vec![rand::thread_rng().gen(); 10],
};
let mut agent = Agent {
epsilon: epsilon,
Qs: vec![0f64; 10],
ns: vec![0f64; 10],
};
let mut total_reward = 0;
let mut total_rewards: Vec<f64> = vec![];
let mut rates: Vec<f64> = vec![];
for step in 0..steps {
// 1. choose an action
let action = agent.get_action();
// 2. get a reward
let reward = bandit.play(action);
// 3. learn from an action and a reward
agent.update(action, reward);
total_reward += reward;
total_rewards.push(total_reward as f64);
rates.push(total_reward as f64 / (step as f64 + 1f64));
}
println!("Total reward: {:?}", total_reward);
// preparate for drawing graphs
let (_, rewards_max) = total_rewards
.iter()
.fold((0.0 / 0.0, 0.0 / 0.0), |(m, n), v| (v.min(m), v.max(n)));
let (_, rates_max) = rates
.iter()
.fold((0.0 / 0.0, 0.0 / 0.0), |(m, n), v| (v.min(m), v.max(n)));
// prepare for drawing a graphs
let mut points_total_rewards = vec![];
let mut points_rates = vec![];
for (i, val) in total_rewards.iter().enumerate() {
points_total_rewards.push(((i + 1) as f64, *val));
}
for (i, val) in rates.iter().enumerate() {
points_rates.push(((i + 1) as f64, *val));
}
// draw a graph1
let root =
BitMapBackend::new("output/bandit/total_reward.png", (1280, 960)).into_drawing_area();
root.fill(&WHITE)?;
let mut chart = ChartBuilder::on(&root)
.caption("Bandit Total Reward", ("sans-serif", 20).into_font())
.margin(10)
.x_label_area_size(50)
.y_label_area_size(50)
.build_cartesian_2d(0f64..1_000f64, 0f64..rewards_max)?;
chart.configure_mesh().draw()?;
chart.draw_series(LineSeries::new(points_total_rewards, &RED))?;
// draw a graph2
let root = BitMapBackend::new("output/bandit/rates.png", (1280, 960)).into_drawing_area();
root.fill(&WHITE)?;
let root = root.margin(10, 10, 10, 10);
let mut chart = ChartBuilder::on(&root)
.caption("Bandit Rates", ("sans-serif", 20).into_font())
.margin(10)
.x_label_area_size(50)
.y_label_area_size(50)
.build_cartesian_2d(0f64..1_000f64, 0f64..rates_max)?;
chart.configure_mesh().draw()?;
chart.draw_series(LineSeries::new(points_rates, &RED))?;
Ok(())
}
描画結果
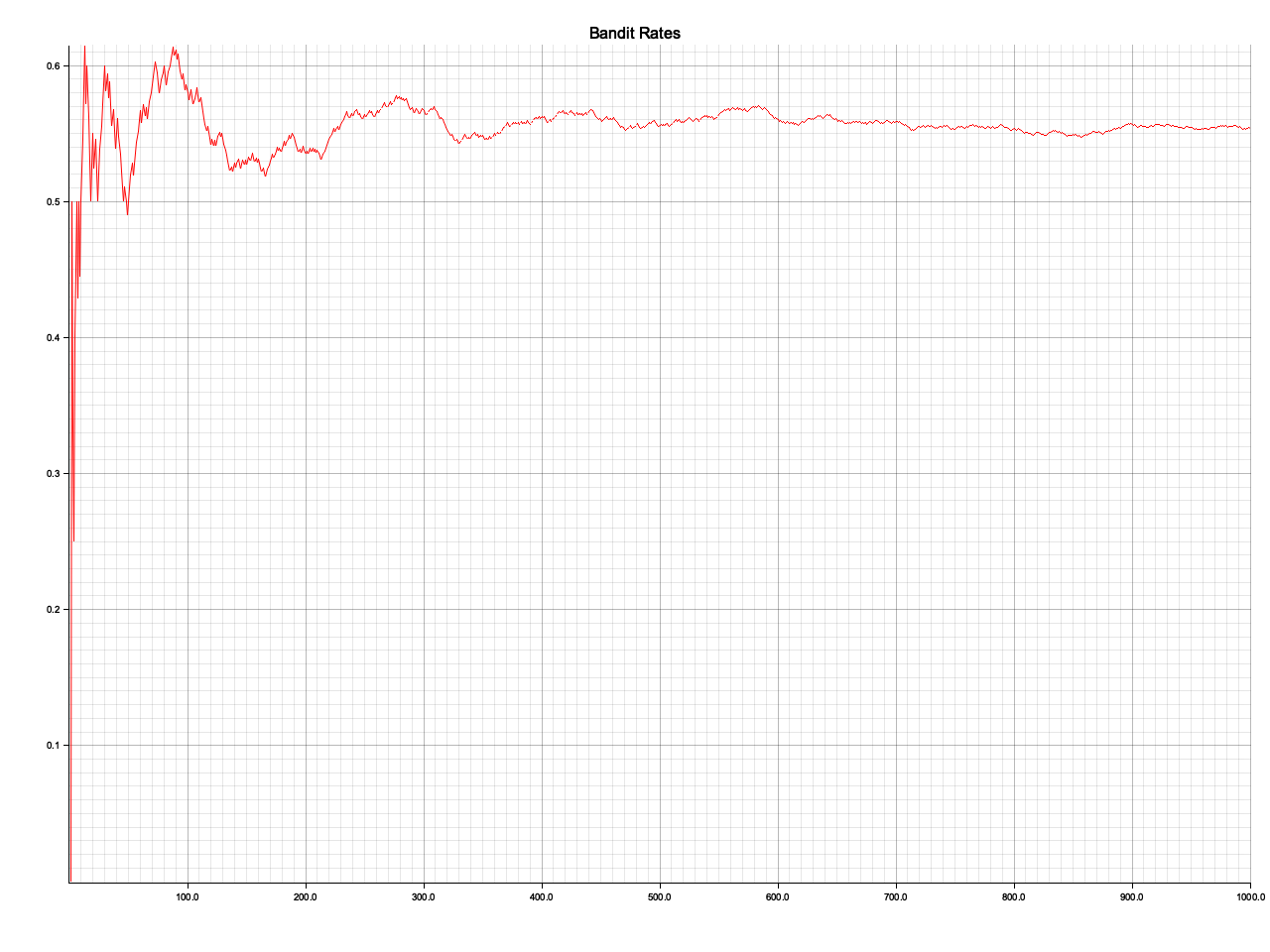
ch01/output/bandit/rates.png
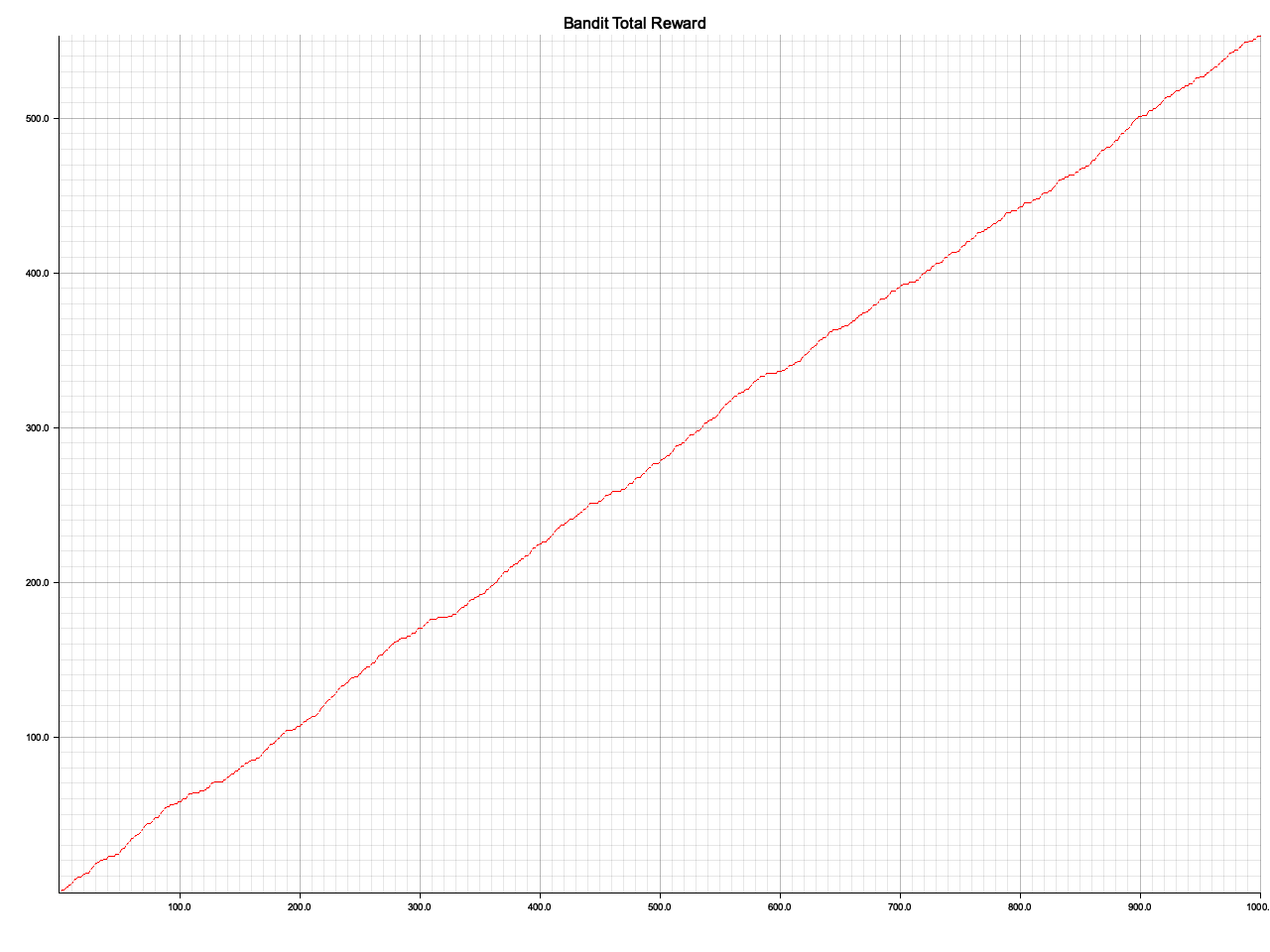
ch01/output/bandit/total_reward.png
非定常問題
ここまでは報酬の確率が常に一定でした。これを定常問題といいます。一方で確率が動的に変動する問題を非定常問題といいます。ここからは非定常問題に取り組んでいきます。
struct NonStatBanditの実装
非定常問題を解くにあたってstruct Banditからの変更点は報酬に重み付けをして古い報酬ほど重み付けを小さくするようにすることです。
ch01/src/non_stationary.rs
use rand::Rng;
pub struct NonStatBandit {
pub arms: usize,
pub rates: Vec<f64>,
}
impl NonStatBandit {
pub fn play(&mut self, arm: usize) -> i32 {
let rate: f64 = self.rates[arm];
self.rates
.iter()
.map(|x| x + 0.1 * rand::thread_rng().gen::<f64>());
let random_num: f64 = rand::thread_rng().gen();
if random_num < rate {
1
} else {
0
}
}
}
struct AlphaAgentの実装
struct Agentとの違いは固定値alphaによる更新を行う機能の追加をするだけです。
ch01/src/non_stationary.rs
use std::cmp::Ordering;
pub struct AlphaAgent {
pub epsilon: f64,
pub Qs: Vec<f64>,
pub alpha: f64,
}
impl AlphaAgent {
pub fn update(&mut self, action: usize, reward: i32) {
self.Qs[action] += (reward as f64 - self.Qs[action]) * self.alpha;
}
pub fn get_action(&self) -> usize {
let random_num: f64 = rand::thread_rng().gen();
if random_num < self.epsilon {
rand::thread_rng().gen_range(0..self.Qs.len()) as usize
} else {
self.Qs
.iter()
.enumerate()
.max_by(|(_, a), (_, b)| a.partial_cmp(b).unwrap_or(Ordering::Equal))
.map(|(index, _)| index)
.unwrap() as usize
}
}
}
おわりに
この記事は1章を読んだ段階で書きました。今後も書く章のコードを書いたら次を更新しようと思います。なぜRustで実装するのかって？趣味です。
Links
今回使用したクレート
Discussion