🧠
量子将棋の収束アルゴリズム

2025/11/08に公開
 告知🏆️量子将棋の世界大会が来週11/14(金)開催されます！🏆️
https://x.com/shogitter_dev/status/1981658071320699034

 はじめに先日個人ブログに投稿した量子将棋のルール詳解という記事への反応として、量子将棋の収束アルゴリズムに関する記事が出されていました[1]。反響があるというのは実に嬉しいものです。
https://note.com/kind_aster978/n/nb6ad5a2bbe33
この記事内でのアルゴリズムの記述は形式化されたもので、正しいアルゴリズムだと思います。この際せっかくなので、筆者が運営する将棋ったーという対局サイト上で実際に走っており、2000局以上の量子将棋の対局を捌いてきたコード[2]を交えながらそのアルゴリズムについて解説できればと思います。個人的には、界隈で量子将棋AIの作成を目論む声を複数聞きますので、そもそも謎めいた量子将棋アルゴリズム理解への一助となれれば幸いです。
なお、実際のコードはこちらのgistで公開しています。
https://gist.github.com/na2hiro/af70792beb897c092a970904b8d3db25

 そもそも量子将棋とは本記事は、量子将棋のルールを理解した読者に向けて書かれています。軽くおさらいします。
公式ルールは次のように端的に書かれています。
量子将棋のルール　駒が量子状態にある。すなわち、最初にあらゆる種類の駒である可能性を持っており、移動するたびにあり得ない駒が除かれ種類が定まっていく。枚数配分は先手後手それぞれ本将棋と同じ。駒を取るとその駒が王である可能性が排除される。王に確定した駒をとれば勝ち。二歩・王手放置は許可。 量子将棋 - 将棋ったー
具体例も交えたルール説明はこちらでしていますので、適宜ご確認ください。
https://na2hiro.hatenablog.com/entry/2025/10/31/量子将棋のルール詳解

 やりたいこと駒は先手後手それぞれ20枚。
最初の段階では、すべての駒が「玉飛角金銀桂香歩」の可能性を持つ
駒は、その動き等により、その可能性が絞られていく（「絞り込み」による収束[3]と呼ぶことにします）。
例：ある駒が１マス前に進んだ場合、角と桂は前に進めないため、その駒が角と桂であったような可能性が除外される。もし「玉飛角金銀桂香歩」の可能性を持った駒が前に動いたら、「玉飛金銀香歩」という６種類の可能性を持った駒に絞られる。

最も重要かつ複雑なことに、先手後手それぞれ20枚の中で配分が「玉１＋飛１＋角１＋金２＋銀２＋桂２＋香２＋歩９」と決まっており、例えばある駒が飛車に収束した場合はそれ以外の駒から飛車の可能性を取り除くといった、「使い切り」の判定が必要。（「使い切り」による収束と呼ぶことにします[4]）
玉に確定した駒が取られたら、終局する。

 実装案これを実装するにあたり、いくつかの案があります。（これらは実装開始当時の案であり、実際はできないものもあるかもしれません）
可能性のある駒種を管理し、うまく駒種の出現数を数えることで使い切りを判定する。
20枚の駒種の可能性の集合を論理式で表現し、局面が進むにつれ追加の論理式を結合していき、SATソルバで充足可能性を判定することで駒種の判定や矛盾の検出を行う。
20枚の駒種の可能性を順列で表現し、局面が進につれ順列の集合に対する演算を行うことで可能性のある順列を絞っていき、駒種の判定や矛盾の検出を行うπDD: Permutation Decision Diagramという順列の集合を効率的に扱えるデータ構造がそれに適していると思われる。
余談ですが、この方法を用いれば、ありうる駒種の組み合わせの数を数えることができるため、ある駒の駒種に対して非決定的な"観測"をすることができます。例えば、「この駒は33%で飛車、67%で香車だ」といったことです。現行の量子将棋ルールでは非決定的な観測はないのですが、量子将棋の原案が出た当初、「駒は取られた時点で完全に観測され、１つの駒種に収束する。もし玉に収束したらその時点で勝ち」というルール案も出回っていました。そういったルールに対応できるのは３案のうちこれだけです。

将棋ったーでは、１番目の案を採用しました。

 実装する関数の全体像runQuantum()のインターフェイスは次のようにします。要点は次のとおりです：

worldが量子駒(SuperPiece = QuantumPiece[])の配列となっており、各要素が可能性の残っている駒種の配列となっている点です。戻り値Resultには、受け取った動き等を加味して収束後のnewWorldが含まれます。
戻り値Resultには同様に、使い切られた駒種の配列fulls: QuantumPiece[]が含まれます。

position、move、moveTypeで、どの駒がどのように動いたかを渡します。（詳細はコメント参照。moveとmoveTypeについては「絞り込みによる収束」の章で説明します。）
どの駒がどのマス目にあるか、現在どちらの陣営に属するかなどの情報は外部で管理することとし、runQuantumはこれに関与しません。
type runQuantum = (
  position: number, // world内のposition番目の駒が動いた
  move: QuantumMove | null, // 動いたベクトル。駒打ちなどの場合はnull
  moveType: MoveType, // 成り等
  world: SuperPiece[] // 現局面における１陣営(初期配置ベース)の全ての駒についての、とり得る種類の集合。移動履歴のない駒は除外されている
) => Result;

/**
 * 駒の種類。（成り駒であるかどうかは別フラグで管理していることに留意）
 */
export type QuantumPiece =
  | "Fu"
  | "Ky"
  | "Ke"
  | "Gi"
  | "Ki"
  | "Ka"
  | "Hi"
  | "Ou";

/**
 * 駒種の重ね合わせ
 */
type SuperPiece = QuantumPiece[];

type Result = {
  newWorld: SuperPiece[];
  fulls: QuantumPiece[];
};

 「絞り込み」による収束「絞り込み」による収束は、比較的単純です。やるべきことは以下の５点だけです。
（前出）駒の相対的な動きにより、その動きをできないような駒種ではないというふうに絞り込まれる
成るという選択をした場合、金か玉である可能性が除外される。（金と玉は成れないため）
駒が取られた場合、取られた駒が玉である可能性が除外される。
例外的に、もともと玉でしかなかった場合には、玉が取られたとみなして終局します。この処理については後述します。

１段目に打たれたり不成で動いた駒は、歩香桂である可能性が除外される。
同様に、２段目では桂が除外される。
runQuantumの冒頭で絞り込み収束を行います。「// move（moveType）に起因する絞り込み制約」というコメントの箇所については次節で説明します。
  // 絞り込み収束
  const currentSuperPiece: SuperPiece =
    // moveに起因する絞り込み制約
    (move === null ? allPieces : move2superPiece(move))
      // moveTypeに起因する絞り込み制約
      .filter(
        (kind: QuantumPiece) => !EXCLUDING_PIECES[moveType].includes(kind)
      );
  let filteredWorld = filter(currentSuperPiece, world, position);
function filter(sp: SuperPiece, world: SuperPiece[], position: number) {
  let newWorld = world.slice();
  if (position < world.length) {
    // 既存の駒に制約をかける
    newWorld[position] = world[position].filter((kind) => sp.includes(kind));
  } else {
    // 初めて動いた駒
    newWorld.push(sp);
  }
  return newWorld;
}

 ステップ1: 駒の動きmoveによる絞り込み収束駒の動きによる絞り込み処理コードを再掲します。
    // moveに起因する絞り込み制約
    (move === null ? allPieces : move2superPiece(move))
駒打ちなど、動きがない場合は絞り込みません。ある場合は、move2superPiece(move)を用いて駒種を算出します。
const move2superPiece = ({ vec, promoted }: QuantumMove) => {
  return movingBoards[promoted ? 1 : 0][vec.x + "," + vec.y];
};

export type QuantumMove = {
  /**
   * 動いたベクトル
   */
  vec: RelXY;
  /**
   * 成り駒が動いたかどうか
   */
  promoted: boolean;
};
movingBoardsの生成コードは長いため元コードを参照してください。movingBoard[成か不成][移動ベクトル]を指定すると、そのマス目に移動可能となるような駒種の配列を返すものです。


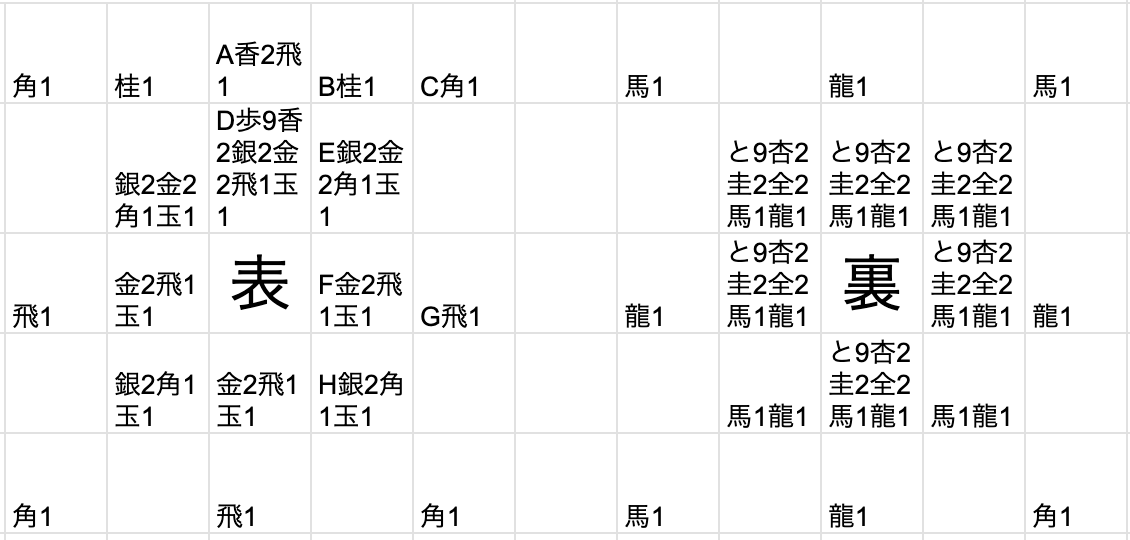
movingBoardsの可視化

 ステップ2: 駒の動きタイプmoveTypeによる絞り込み収束コード駒の動きタイプによる絞り込み処理コードを再掲します。
      // moveTypeに起因する絞り込み制約
      .filter(
        (kind: QuantumPiece) => !EXCLUDING_PIECES[moveType].includes(kind)
      );
単純にケースごとに固定の駒種に絞り込みます。
export enum MoveType {
  Promote, // 成った
  NoPromote1, // １段目打ちか不成
  NoPromote2, // ２段目打ちか不成
  Captured, // この駒が取られた
  Normal, // それ以外
}

const EXCLUDING_PIECES: { [moveType in MoveType]: SuperPiece } = {
  [MoveType.Promote]: ["Ki", "Ou"],
  [MoveType.NoPromote1]: ["Fu", "Ky", "Ke"],
  [MoveType.NoPromote2]: ["Ke"],
  [MoveType.Captured]: ["Ou"],
  [MoveType.Normal]: [],
};

 「使い切り」による収束さて、ここで肝心の「使い切り」について見ていきましょう。ある駒が動いた後、それ以外の駒の持つ可能性が狭まるという収束処理は、一体どのように行えばいいのでしょうか。

 使い切りに関する思考実験どんな時に駒を使い切ってしまうのかを考えてみましょう。
ここでは、簡単のため、「飛香・飛香・飛香」といった表記方法を導入します。これは、ある局面において、絞り込みによる収束後に飛車か香車のどちらかであるような駒が３枚発生し、それ以外の駒は一度も動いたり取られたりしていないことを意味します。
例1）「飛」（例えばある駒が２つ横に移動し、飛車に収束した）の時、飛車の配分は１枚であるため、この時点で飛車は使い切りとなる（それ以外の駒から飛車の可能性が取り除かれる）
例2）「桂・桂」の時、桂馬の配分は２枚であるため、桂馬が使い切りとなる。
例2'）「桂・桂歩」の時、桂+歩の配分の和は2+9=11枚>2枚であるため、使い切りとなる駒はない。
例3）「飛香・飛香・飛香」の時、飛と香の配分の和は2+1=3枚であるため、飛車と香車が使い切りとなる。
例4）「飛香・飛香」の時、飛と香の配分の和は2+1=3枚<２枚であるため、まだ使い切りは起こらない。続いて別の駒が「飛」に確定して「飛香・飛香・飛」となった時、飛と香の配分の和は2+1=3枚に達して飛香が使い切りとなる。なお、最後の駒が飛車に確定するため、もともと「飛香」だった最初の２枚は「香」に確定する。
例5）「銀・銀角・銀角・金銀・金銀」の時、角、金、銀の配分の和は1+2+2=5枚のため、角金銀は使い切りとなる。
例5'）「銀・銀角・銀角・金銀・金銀飛」の時、飛、角、金、銀の配分の和は1+1+2+2=6枚<5枚のため、使い切りとなる駒はない。
例1や例2など単一の駒種が使い切られる例の判定は簡単にできそうですが、問題は例3以降で、飛車か香車という駒が３枚出現した場合のように、駒種が１つに確定する前の段階の駒も使い切りに寄与するのです。また、使い切りに関与するすべての駒がもつ駒種すべてが同時に使い切られていることもわかります。

 使い切りの検出の方針最もナイーブには、駒種のすべての組み合わせ（すなわち、集合{玉,飛,角,金,銀,桂,香,歩}のすべての部分集合のうち非空なもの）に対して、そういった駒種の全部または一部のみからなるような駒の枚数を数え、それが配分の和と一致しているかどうかを確かめれば、使い切りの駒種を調べ上げることができます。2^8-1=255通りを確かめるわけです。冒頭の記事でもこの様なアプローチが定式化されています。
本コードでは、駒種の組み合わせの生成を、現局面で存在している駒種の組み合わせのみに絞ることにより多少の最適化[5]をしています。また、一度も動いていない駒は使い切りに寄与することはないので、考慮に入れません。（runQuantumの入出力に使われるworld配列が一度も動いていない駒を含まないのはそのためです）
なお、コード中では、駒種の配分を使い切るような駒は、「相見合い」をしているという言葉を使っています。「相見合い」という用語は、関 勝寿さん(@seki)による量子詰将棋の定義を参考にしました。
使い切りの処理は次の４ステップで行います。順に説明していきます。
相見合いしている駒種グループを返す
使い切り駒種の算出
相見合いグループのコンパクト化
世界の再構築

 ステップ1: 相見合いしている駒種グループを返すextractAimiaiGroups()では駒種ごとに駒をグループ化した後、相見合いとなる駒種グループを列挙します。
/**
 * 全ての相見合いグループを返す。超過相見合いが発生したらエラーを投げる
 * @param world
 */
function extractAimiaiGroups(
  world: SuperPiece[]
): SuperPieceGroup[] {
  /* ステップ1-1: 駒種ごとのグループ化 */
  /* ... */
  /* ステップ1-2：全組み合わせから使い切りを判定し、相見合いしている駒種グループを返す */
  /* ... */
}

/**
 * とある駒種の重ね合わせを持った駒のpositionすべて
 */
type SuperPieceGroup = {
  superPiece: SuperPiece;
  positions: number[];
};

 ステップ1-1: 駒種ごとのグループ化まずはworldを駒種ごとにグループ化します。
  // ステップ1-1: 駒種ごとのグループ化
  // 同一のsuper pieceである駒をグループ化（同一のsuper pieceは、必ず同一の相見合いを構成するため）
  let superPieceGroups = groupSuperPieces(world);
  function groupSuperPieces(world: SuperPiece[]): SuperPieceGroup[] {
    const superPiece2Possibility: {
      [superPieceHash: string]: SuperPieceGroup;
    } = {};
    world.map((superPiece, index) => {
      const superPieceHash = hashSuperPiece(superPiece);
      if (!superPiece2Possibility[superPieceHash])
        superPiece2Possibility[superPieceHash] = {
          superPiece,
          positions: [],
        };
      superPiece2Possibility[superPieceHash].positions.push(index);
    });
    return Array.from(Object.values(superPiece2Possibility));
  }
「飛香・飛香・飛」という３つの収束しつつある駒があり、それ以外は一度も動いていないような局面の場合、入出力はこのようになります。
入力 world = [["Hi","Ky"],["Hi","Ky"],["Hi"]]
出力 superPieceGroups = [{superPiece: ["Hi","Ky"], positions: [0, 1]}, {superPiece: ["Hi"], positions: [2]}]

 ステップ1-2：駒種グループの全組み合わせに対して使い切りを判定し、相見合いしている駒種グループを返すまずはsuperPieceGroupsのすべての非空の部分集合を列挙します。
  // ステップ1-2：全組み合わせから使い切りを判定し、相見合いしている駒種グループを返す
  const allNonemptySubsetsOfGroups = getAllSubsets(superPieceGroups).slice(1);
getAllSubsets()はすべての部分集合を求める関数です。例えばgetAllSubsets([0,1,2])の戻り値は[[],[0],[1],[1,0],[2],[2,0],[2,1],[2,1,0]]などとなります。slice(1)をすることで不要な[]を取り除いています。
先ほどの「飛香・飛香・飛」の例を元にすると、allNonemptySubsetsOfGroups = [[{superPiece: ["Hi","Ky"], positions: [0, 1]}], [{superPiece: ["Hi"], positions: [2]}], [{superPiece: ["Hi","Ky"], positions: [0, 1]}, {superPiece: ["Hi"], positions: [2]}]]となります。
あとは、それぞれのsuperPieceGroup部分集合ひとつひとつ(subsetOfGroups)について、そこに含まれる駒の枚数positions.lengthと、そこに含まれるすべての駒種の配分max = calcMax(superPiece)を比較します。
もし一致する場合は使い切っていることとなり、使い切った駒種をsuperPieceとして、それらの駒のpositionsを戻し、ステップ3以降で利用します。
もし超過する場合は矛盾しているため、例外を投げます。
このパスは、玉でしかない駒が取られた場合に必要になります（後述）。駒種が空集合となり配分は0枚のところ、1枚存在すると判定されるわけです。また、そもそも前に進めない角などでしかないのに前に進もうとした場合にその指し手を弾くためにも使えます。

もし駒数が配分を下回る場合は問題ないため無視してよく、戻り値からは取り除きます。
  return allNonemptySubsetsOfGroups
    .map((subsetOfGroups) => {
      const pieceSet = new Set<QuantumPiece>();
      let positions: number[] = [];
      subsetOfGroups.forEach(({ superPiece, positions: ps }) => {
        superPiece.forEach((p) => pieceSet.add(p));
        positions = positions.concat(ps);
      });
      const superPiece = Array.from(pieceSet);
      const max = calcMax(superPiece);
      // console.log(max, superPiece, superPiece.length, positions, positions.length)
      if (positions.length > max) {
        // 超過相見合い：このpositions全てをsuperPieceのどれかで確定しようとすると、多すぎる
        throw new QuantumContradictionError("そのような動きはあり得ません");
      }
      if (positions.length < max) {
        // 相見合いしていない
        return null;
      }
      return { superPiece, positions };
    })
    .filter((x) => x !== null);
配分maxは次のcalcMax(superPiece: SuperPiece)で算出します。
const initialPieces: { [piece in QuantumPiece]: number } = {
  Fu: 9,
  Ky: 2,
  Ke: 2,
  Gi: 2,
  Ki: 2,
  Ka: 1,
  Hi: 1,
  Ou: 1,
};
/**
 * superPieceがmax枚あったら相見合いになる、そのmaxを返す
 * @param superPiece
 */
function calcMax(superPiece: SuperPiece) {
  return superPiece.map((p) => initialPieces[p]).reduce((a, b) => a + b, 0);
}
「飛香・飛香・飛」の例だと、この３枚のグループと「飛」だけのグループの２グループが返されます。[{superPiece: ["Hi"], positions: [2]}, {superPiece: ["Hi","Ky"], positions: [0, 1, 2]}]

 ステップ2: 使い切り駒種の算出使い切った駒種を算出し、まだ一度も動いていない駒の駒種の列挙に使えるようにします。
const fullSet = calculateFullSet(aimiaiSuperPieceGroups);
これは、単純に相見合いグループに出現する駒種の和集合です。
/**
 * 使い切られている駒種を得る
 * @param aimiaiSuperPieceGroups
 */
function calculateFullSet(aimiaiSuperPieceGroups: SuperPieceGroup[]) {
  const fullSet = new Set<QuantumPiece>();
  // 相見合いを構成する駒種は、全て使い切られている
  aimiaiSuperPieceGroups.forEach(({ superPiece }) =>
    superPiece.forEach((p) => fullSet.add(p))
  );
  return fullSet;
}

 ステップ3: 相見合いグループのコンパクト化続いて、相見合いグループに対してコンパクト化を行います。「飛香・飛香・飛」の例で見ると、extractAimiaiGroups()が飛と香の使い切りを検出しましたが、相見合いグループ内を見ると３枚目が飛を使い切り、１，２枚目から飛の可能性を取り除く必要がある部分に相当します。
  const compactedGroups = compactAimiai(aimiaiSuperPieceGroups);
ここでは、繰り返し"最小"の相見合いグループから駒種を確定していき、確定した駒種はそれ以外のグループから除外していきます。ここで最小とは、それ以外のどの集合にも包含されている集合を意味します。なお、本コードでは必ず"最小"が存在すると仮定しており、それで正常に動作しています。
/**
 * 最小相見合いから順に駒種を確定させていく
 * @param aimiaiSuperPieceGroups
 */
function compactAimiai(
  aimiaiSuperPieceGroups: SuperPieceGroup[]
): SuperPieceGroup[] {
  aimiaiSuperPieceGroups = aimiaiSuperPieceGroups.filter(
    (detail) => detail.superPiece.length > 0
  );
  const determinedGroups: SuperPieceGroup[] = [];
  while (aimiaiSuperPieceGroups.length > 0) {
    // 繰り返し最小グループを探す
    const foundIndex = aimiaiSuperPieceGroups.findIndex(({ superPiece: x }) => {
      // 全てのグループのSuperPieceであるxxが、とあるグループxと同じかxのsupersetである場合、xは最小である
      return aimiaiSuperPieceGroups.every(
        ({ superPiece: xx }) => superPieceEquals(x, xx) || !isSubsetOf(xx, x)
      );
    })!;
    // 最小グループを取り除く
    const [found] = aimiaiSuperPieceGroups.splice(foundIndex, 1);
    determinedGroups.push(found);

    // 該当する最小グループの駒種を他の相見合いの駒種から取り除く
    aimiaiSuperPieceGroups = aimiaiSuperPieceGroups
      .map(({ superPiece, positions }) => ({
        superPiece: superPiece.filter(
          (kind) => !found.superPiece.includes(kind)
        ),
        positions: positions.filter((i) => !found.positions.includes(i)),
      }))
      // TODO: いらないかも
      .filter(({ superPiece }) => superPiece.length > 0);
  }
  return determinedGroups;
}
「飛香・飛香・飛」の例[{superPiece: ["Hi"], positions: [2]}, {superPiece: ["Hi","Ky"], positions: [0, 1, 2]}]だと、{飛}⊂{飛,香}ですから、飛のほうが最小となり、foundに{superPiece: ["Hi"], positions: [2]}が入りこれがdeterminedGroupsにもpushされます。その後、残りの相見合いグループ全てからこの確定グループの除外が起こります。

superPieceから"Hi"が除外されます

positionsから"Hi"に確定したpositions = [2]が除外されます。
その結果、残った相見合いグループは{superPiece: ["Ky"], positions: [0, 1]}となり、whileループの２周目に入ります。２周目はこの残ったグループが最小となり、determinedGroupsに追加され、ループを抜けます。
結果として、[{superPiece: ["Hi"], positions: [2]},{superPiece: ["Ky"], positions: [0, 1]}]が返されます。最初の２つの駒が香に確定し最後の駒が飛に確定したことを表します。
相見合いしている駒はこれで全て確定しました。

 ステップ4: 世界の再構築これで必要な情報は出揃いました。あとはこれらを用いてnewWorldを構築します。

filteredWorld: 動いた駒のみが絞り込み収束した世界

compactedGroups: コンパクトな相見合いグループとそれらの駒種

fullSet: 使い切り駒種

 ステップ4-1: 相見合いグループの部分世界への変換相見合いしている駒を世界worldの形式に戻しやすくするため、相見合い駒のみからなる部分世界を作成します。これは、相見合いしている駒のworldで、相見合いしていない駒には何も入っていない（undefinedが入っている）ような部分的なworldを指します。
  const aimiaiPartialWorld =
    convertSuperPieceGroupsToPartialWorld(compactedGroups);
function convertSuperPieceGroupsToPartialWorld(
  superPieceGroups: SuperPieceGroup[]
): SuperPiece[] {
  let ret: SuperPiece[] = [];
  superPieceGroups.forEach(({ superPiece, positions }) =>
    positions.forEach((i) => {
      ret[i] = superPiece;
    })
  );
  return ret;
}

 ステップ4-2: 相見合い駒とfullSetのfilteredWorldへの反映ステップ4-1で作成した部分世界aimiaiPartialWorldとfullSetをfilteredWorldに併合することで完全なworldを構築します。これがrunQuantumの戻り値に使われます。
  const newWorld = filteredWorld.map((superPiece, i) => {
    const aimiaiSuperPiece = aimiaiPartialWorld[i];
    if (aimiaiSuperPiece) {
      // 相見合いがある場合はそれを制約とする（使い切られた駒は相見合い確定時に適宜取り除かれているためfullsを使う必要はない）
      return superPiece.filter((sp1) => aimiaiSuperPiece.includes(sp1));
    }
    // 使い切られた駒を取り除く
    return superPiece.filter((sp1) => !fullSet.has(sp1));
  });
やや長大でしたが、これで使い切りの処理は全てです。

 玉が取られたケースの処理ステップ1-2で、玉に確定した駒取られた際には例外が投げられると述べましたが、量子将棋のルールは、玉に確定した駒が取られたら、玉のまま駒台に載せて終局するのでした。これは、ステップ1をtryで囲み、駒取りであって例外が投げられた場合は玉取りであったとして、その駒が取られたという処理をせず玉であったとみなすfilteredWorldを作り直してステップ1をやり直すことで実現しています。
  let aimiaiSuperPieceGroups;
  try {
    aimiaiSuperPieceGroups = extractAimiaiGroups(filteredWorld);
  } catch (e) {
    if (
      moveType === MoveType.Captured &&
      e instanceof QuantumContradictionError
    ) {
      // 駒取りでは王の可能性が取り除かれる。もしそれで矛盾が発生した場合、それは取った駒が王だったからに他ならない。ここで例外的に取った駒を王将とする（終局）
      filteredWorld = filter(["Ou"], world, position);
      aimiaiSuperPieceGroups = extractAimiaiGroups(filteredWorld);
    } else {
      throw e;
    }
  }
これで収束を計算する関数の中身はすべてです。

 収束アルゴリズム最後に、この収束を計算する関数を使った、収束アルゴリズムについて述べます。
初期局面では、先手後手陣営ともworld = []かつfulls = []とする。
駒が動いた場合は、その動いた駒が元々属していた陣営の20枚についてrunQuantum(position, move, moveType, world)を呼び出し、新たなworldで置き換える。
もしその時駒を取っていた場合は、引き続き、取られた駒が元々属していた陣営の20枚についてrunQuantum(position, null, MoveType.Captured, world)を呼び出し、新たなworldで置き換える

駒が打たれた場合、それが敵陣２段目以内だった場合にのみ、runQuantum(position, null, MoveType.NoPromote1(か2), world)を呼び出し、新たなworldで置き換える。
なお、上記runQuantum()を呼ぶにあたり必要となる次の情報を保持する。各駒について、
とある時点での所属にかかわらず、一番最初に属していた陣営がどちらであったかの情報
動いたり取られたりなどしてrunQuantum()実行の対象となる駒の然るべきposition情報。このpositionは、同一の駒が過去に呼び出されていた場合はその時に使ったpositionを、そうでない場合には払い出されたpositionのうち最大のものに1を加えた新しいpositionを渡すようにする。


 高速化できそうな点このアルゴリズムは将棋ったー上での対人対局の裁定と、簡単なAIのエンジンに問題なく使用されているものの、速度に対する最適化はさほど行われていません。もし本格的な量子将棋AIを作成する場合にはここが局面生成のボトルネックになりえます。どういった高速化ができそうか、今後のために私見を記すことにします。
駒種の集合をbitsetで扱う
ステップ1-2のextractAimiaiGroups内ですべての駒種の部分集合を列挙しているが、これが場合によっては大きな場合の数になる可能性がある。その後ステップ3で最小の駒種からコンパクト化するくらいなら、最初から最小の駒種のようなものから検査していくことはできないか。
そもそもこの駒種の部分集合の列挙が2^8を超えるケースもあり場合によってはナイーブ案より性能が悪化する可能性がある。例えば「銀」「角」「銀角」という３枚があった場合、本アルゴリズムだと2^3-1=7通りを調べるが、銀と角に関しての組み合わせ総数は2^2-1=3通り（銀、角、銀角）しかない。（「銀角」を含まずに「銀」「角」の２枚について配分を計算してしまっている）ナイーブ案を試したほうがいいかもしれない。

fullsも次のrunQuantumの入力として活用すれば、余分な可能性を最初から除外できるかもしれない。例えば飛に確定した駒がいくら他の駒種グループ（例えば香に確定した駒２枚）と相見合いを構成しても、結局は世界になんの影響も与えないため。（fullsよりも詳細な、もう確定しきった駒種のリストを計算し保持しておく必要があるかもしれない）

 おわりに量子将棋の世界大会、ぜひエントリー・拡散のほうよろしくお願いいたします🙇
https://x.com/shogitter_dev/status/1981658071320699034

脚注
著者のハイチュウリツさんは、量子将棋の序盤研究に関する記事も書かれているので、興味のある方はご覧ください ↩︎
2013年10月から2025年10月まで12年間の累計局数。途中移植とリファクタリングが挟んでいるため同一のコードがこの局数を捌いたわけではありません。 ↩︎
冒頭のハイチュウリツさんの記事では、局所収束と呼ばれています ↩︎
冒頭のハイチュウリツさんの記事では、大域収束と呼ばれています ↩︎
今考え直したところ、これはナイーブな例より性能が悪化する可能性がありそうです。高速化の章で触れることにします。 ↩︎
量子将棋の収束アルゴリズム

告知

はじめに

そもそも量子将棋とは

やりたいこと

実装案

実装する関数の全体像

「絞り込み」による収束

ステップ1: 駒の動き`move`による絞り込み収束

ステップ2: 駒の動きタイプ`moveType`による絞り込み収束コード

「使い切り」による収束

使い切りに関する思考実験

使い切りの検出の方針

ステップ1: 相見合いしている駒種グループを返す

ステップ1-1: 駒種ごとのグループ化

ステップ1-2：駒種グループの全組み合わせに対して使い切りを判定し、相見合いしている駒種グループを返す

ステップ2: 使い切り駒種の算出

ステップ3: 相見合いグループのコンパクト化

ステップ4: 世界の再構築

ステップ4-1: 相見合いグループの部分世界への変換

ステップ4-2: 相見合い駒とfullSetの`filteredWorld`への反映

玉が取られたケースの処理

収束アルゴリズム

高速化できそうな点

おわりに

Discussion
