🎼

DyadにおけるHarmonic Entropy

2022/01/31に公開

Python

音楽

音楽理論

tech

概要

音がいかにハモっているかという指標に「Harmonic Entropy」というのがあります。
https://en.xen.wiki/w/Harmonic_entropy

基本的な考え方は以下の通りです。

The general idea of Harmonic Entropy is to first develop a discrete probability distribution quantifying how strongly an arbitrary incoming dyad "matches" every element in a set of basis rational intervals, and then seeing how evenly distributed the resulting probabilities are. If the distribution for some dyad is spread out very evenly, such that there is no clear "victor" basis interval that dominates the distribution, the dyad is considered to be more discordant; on the other extreme, if the distribution tends to concentrate on one or a small set of dyads, the dyad is considered to be more concordant.

つまり、入力音程がある有理音程(=純正律の音程)であると強く知覚できる場合に「協和している」、突出した有理音程がなくどの有理音程ともつかない場合に「不協和である」というわけです。

アプローチとしては、あらゆる有理音程に対する入力音程がその音程に聞こえる確率を定義し、その確率分布のシャノン情報量を計算します。シャノン情報量が多いということは、無数にある有理音程の中から特定の有理音程であると強く判断できることを意味します。

台が有限集合の確率空間 $\Omega$ 、および $\Omega$ 上の確率分布 $P$ が与えられた時、 $P$ のシャノン情報量は、各事象 $A\in \Omega$ の選択情報量 $- { \rm log} P(A)$ の期待値

H(A) = -\sum_{A \in \Omega} P(A){ \rm log}P(A)

として定義されます。

定義

まず $P$ を、あるインターバル $c$ が純正律 $j$ と知覚される確率とします。 $P(J=5/4|C=400¢)$ は、400セント(すなわち平均律の長三度)が5/4(すなわち純正律の長三度)と知覚される確率です。

この確率 $P$ は、今の所は以下のような性質を持つものとします。

$c$ が $j$ に近いほど大きい
$j$ が簡単な分数であるほど大きい

この時、 $c$ のハーモニックエントロピー $H(c)$ を、任意の有理音程上の $P$ のシャノン情報量と定義します。

H(J|c) = -\sum_{j \in J} P(j|c){ \rm log}P(j|c)

he.py

def calcDyadHE(c):
    js = rationals()
    return shannonEntropy(js, c)
    
def shannonEntropy(js, c):
    s = 0
    for j in js:
        a = p(j, c, js)
        s -= a * np.log1p(a)
    return s

ちなみにnp.log1pを用いているのは、確率がほとんど0に張り付くからです。

有理数の生成と「高さ」

ここで、rationals()で任意の有理数を生成していますが、プログラム上は有限個に区切らなければなりません。そのため複雑性に上限を設けるのですが、有理数に「高さ」の概念を導入する必要があります。

有理数 $n/d$ に対して、 $\sqrt{nd}$ を用いる「Tenney height」と、 $1/{\rm max}(j_n, j_d)$ を用いる「Weil height」の2種類がよく使われるようです。今回は実装が簡単なWeil heightを採用します。

$[0,1]$ の区間において、Weil heightが $N$ 以下の有理数の集合は $N$ 次のファレイ数列に他ならないので、区間全体としては1ずつ区切って生成します。以下ではとりあえず0から3(無限に低音から1オクターブ半上)まで生成しています。
境界となる $N$ は100とすることが多いようですが、全然計算が終わらないので今回は50にしてあります。

he.py

def rationals(o=50, interval=(0,3)):
    rs = []
    for i in range(interval[0], interval[1]):
        rs.extend(farey(o, i))
    rs.pop(0) # remove 0/1
    print(rs)
    return rs

def farey(n, k):
    if n == 1:
        return [(k,1), (k+1,1)]
    else:
        return deepen(farey(n-1, k) , n)

def deepen(arr, k):
    n = len(arr)
    for i in range(n - 1): 
        l = arr[n - i - 2]
        r = arr[n - i - 1]
        num = l[0] + r[0]
        denom = l[1] + r[1]
        if(denom < k + 1):
            arr.insert(n - i - 1, (num, denom))
    return arr

確率分布

次に、ある音が他の音に聞こえるかどうかの確率分布を考えます。これは、先ほどの

$c$ が $j$ に近いほど大きい

を満たす必要があります。
ガウス分布で、標準偏差が約17セントほどと設定することが多いようです。

S(x-c) = \dfrac{1}{\sigma\sqrt{2\pi}}\exp(-\dfrac{(x-c)^ 2}{2\sigma^ 2})

分布はガウス分布とするのが一般的ですが、ラプラス分布などを設定する例もあるようなので、念の為一般化ガウス分布(GGD)で記述しておきます。

he.py

def s(x, c):
    return ggd(frac2cent(x), c, 17*1.414, 2)

def frac2cent(x):
    return 1200 * np.log2(x)

from scipy.special import gamma
def ggd(x, mu, alpha, beta): 
    return beta / (2 * alpha * gamma(1/beta)) * np.exp(-np.power(np.abs(x - mu)/alpha, beta))

Domain-Integral Probabilities

さて、いよいよ任意の音程に対するスコアを計算します。このスコアは、先ほどの

$j$ が簡単な分数であるほど大きい

を満たす必要があります。
まず、任意の音程を有理音程 $j$ の「領域(domain)」に分割します。
$k$ 番目の有理数 $j_k$ の領域 $(j_u), (j_l)$ は、それぞれ隣の有理数との「中間値(mediant)」までと定義します。

j_u = {\rm med}(j_k, j_{k+1})\\ j_l = {\rm med}(j_{k-1}, j_k)

こうすると、簡単な有理数は隣との間隔が広いので大きな領域を獲得し、複雑な有理数は領域が狭くなります。

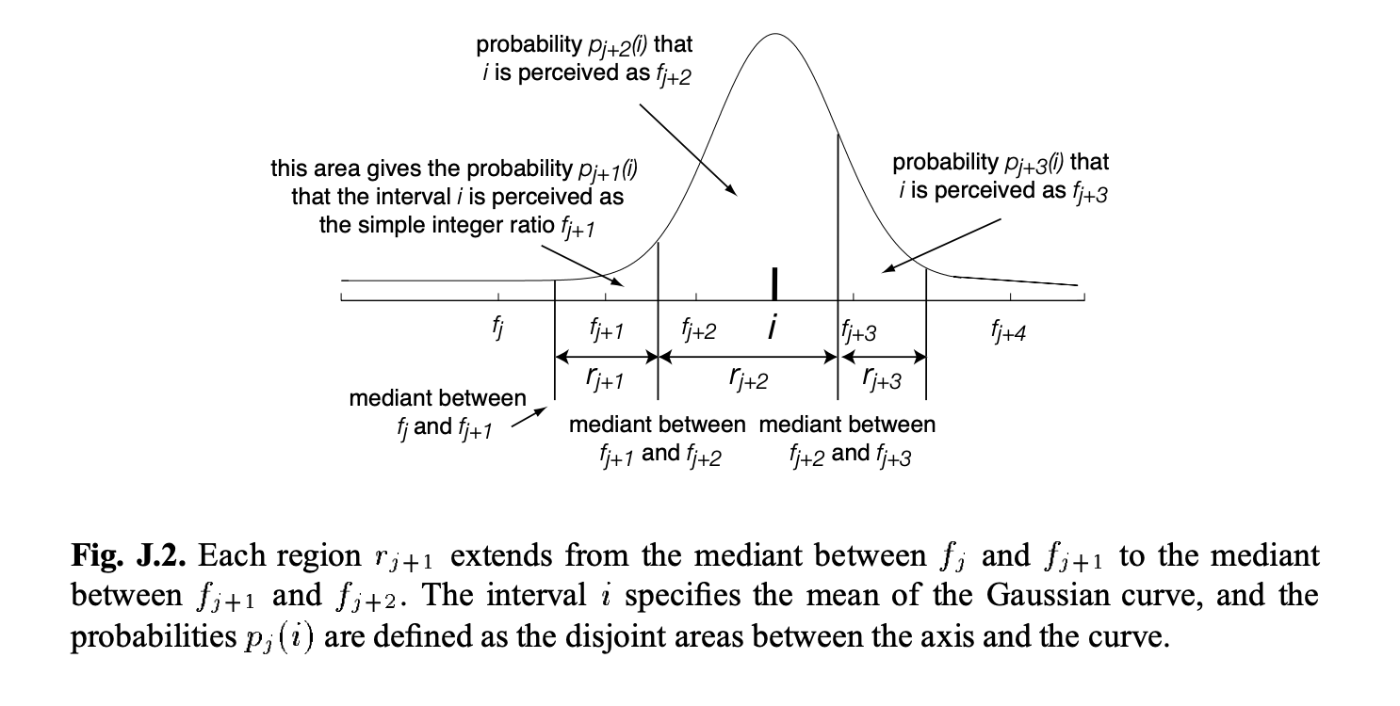
そして、ある音程 $c$ が $j$ に聞こえる確率を、先ほどの確率分布における $(j_u), (j_l)$ 間の面積であると考えます。

P(j|c) = \int^{¢(j_u)}_{¢(j_l)}S(x-c)dx

これは、先ほどの

$j$ が簡単な分数であるほど大きい

を満たしています。

Simple Weighted Probabilities

しかしながら、積分は解析解を求めるのが大変なので、プログラム上では近似を行います。有理数群の「高さ」にTenney height を用いた場合は、 $N$ が十分大きい場合は $\frac{1}{\sqrt{nd}}$ の重みをかけることで近似できるようです。

Q(j|c) = \frac{S(¢(j)-c)}{\sqrt{j_n \cdot j_d}}

同じようにWeil heightを用いた場合は $\frac{1}{{\rm max}(j_n, j_d)}$ で近似できるようです。

Q(j|c) = \frac{S(¢(j)-c)}{{\rm max}(j_n, j_d)}

he.py

def q(j, c):
    jn = j[0]
    jd = j[1]
    return s(jn / jd, c) / h(jn, jd)

def h(jn, jd, t="Weil"):
    if t == "Tenney":
        return np.sqrt(jn * jd)
    elif t == "Weil":
        return max(jn, jd)

ちなみにこの $Q$ は総和は1にならないので、確率にするために正規化します。

P(j|c) = \frac{Q(j|c)}{\sum_{j \in J}Q(j|c)}

he.py

def p(j, c, js):
    s = 0
    for ji in js:
        s += q(ji, c)
    return q(j, c) / s

プロット

matplotlibで描画してみます。1オクターブとちょっと(¢1500)で計算しました。

plotDyad.py

import numpy as np
import matplotlib.pyplot as plt
from he import calcDyadHE

C = 1000
x = np.linspace( 0, 1500, C)
y = calcDyadHE(x)
plt.plot(x, y)
plt.show()
plt.savefig('fig.png')

log1pで計算したので負になっていますが、本来ならばエントロピーは非負の値になります。

¢0は完全なユニゾンなので当然として、¢1200は1オクターブ上のユニゾンなので突出していますね。
¢700あたりは完全5度(3/2)、¢500あたりは完全4度(4/3)です。その他、¢400の長三度(4/5)、¢900の短七度(7/4)も目立っています。

まとめ

全てのコードはここに置いてあります。

次回は和音に拡張しようと思います。

概要

定義

有理数の生成と「高さ」

確率分布

Domain-Integral Probabilities

Simple Weighted Probabilities

プロット

まとめ

Discussion