🗾

2地点の距離ぐらいExcelで計算しまっしょい & 複数地点↔︎複数地点の総当たり距離も一撃で計算しまっしょい

2023/02/02に公開

Excel

Google Sheets

tech

概要

Google Distance Matrix APIというのがあって、M個の出発地点からN個の到着地点までの距離( $= M \times N$ 通り)を一撃で求められます。

このAPIの強みは住所をテキストで指定することができるところなわけなのですが、仮に各地点の緯度と経度がわかっている場合には、APIなど叩かずとも簡単な計算で求められるんじゃないか？と思いました。

調べると、数ある近似式の中で計算量と誤差のバランスが良さそうなのがヒュベニの公式というもので、回転楕円体としての近似です。

さらに調べていくとExcelでこの式を計算している人がいたので、この方針で実装していくこととします。

ヒュベニの公式

地球を回転楕円体と近似する公式の一つ。

点 $p, q$ 間の距離は、以下の式で近似されます。

D(p, q) = \sqrt{(\Delta_{lon} \cdot M)^2 + (\Delta_{lat} \cdot N \cdot \cos \mu_{lat})^2}

ここで、

\begin{aligned} \Delta_{lat} &= p_{lat} - q_{lat} \\ \Delta_{lon} &= p_{lon} - q_{lon} \\ \mu_{lat} &= \frac{p_{lat} + q_{lat}}{2} \\[20pt] M &= \frac{R_x(1 - E^2)}{W^3} \\ N &= \frac{R_x}{W} \\ W &= \sqrt{1 - E^2 \cdot \sin ^{2} \mu_{lat}} \\ E &= \sqrt{\frac{R_x^2 - R_y^2}{R_x^2}} \\ \end{aligned}

です。ちなみに $M$ は子午線曲率半径、 $N$ は卯酉線曲率半径、 $E$ は離心率です。

また、赤道半径 $R_x$ と極半径 $R_y$ は以下としました(WGS84楕円体)。

\begin{aligned} R_x &= 6378137 \\ R_y &= 6356752.314 \end{aligned}

2点間の距離

早速実装してみます。

=SQRT((($A3-C$1)*PI()/180*6378137*(1-0.00669437999)/SQRT(1-0.00669437999*SIN(($A3+C$1)/2*PI()/180)^2)^3)^2+(($B3-C$2)*PI()/180*6378137/SQRT(1-0.00669437999*SIN(($A3+C$1)/2*PI()/180)^2)*COS(($A3+C$1)/2*PI()/180))^2)

できました。
A3, B3 に出発地点の緯度経度、C1, C2 に到着地点の緯度経度を入力します。

テスト

新宿駅-池袋駅間の距離を計算してテストしてみましょう。

4674.17167754729 m でした。

国土地理院のサイトでも計算して比べてみます。

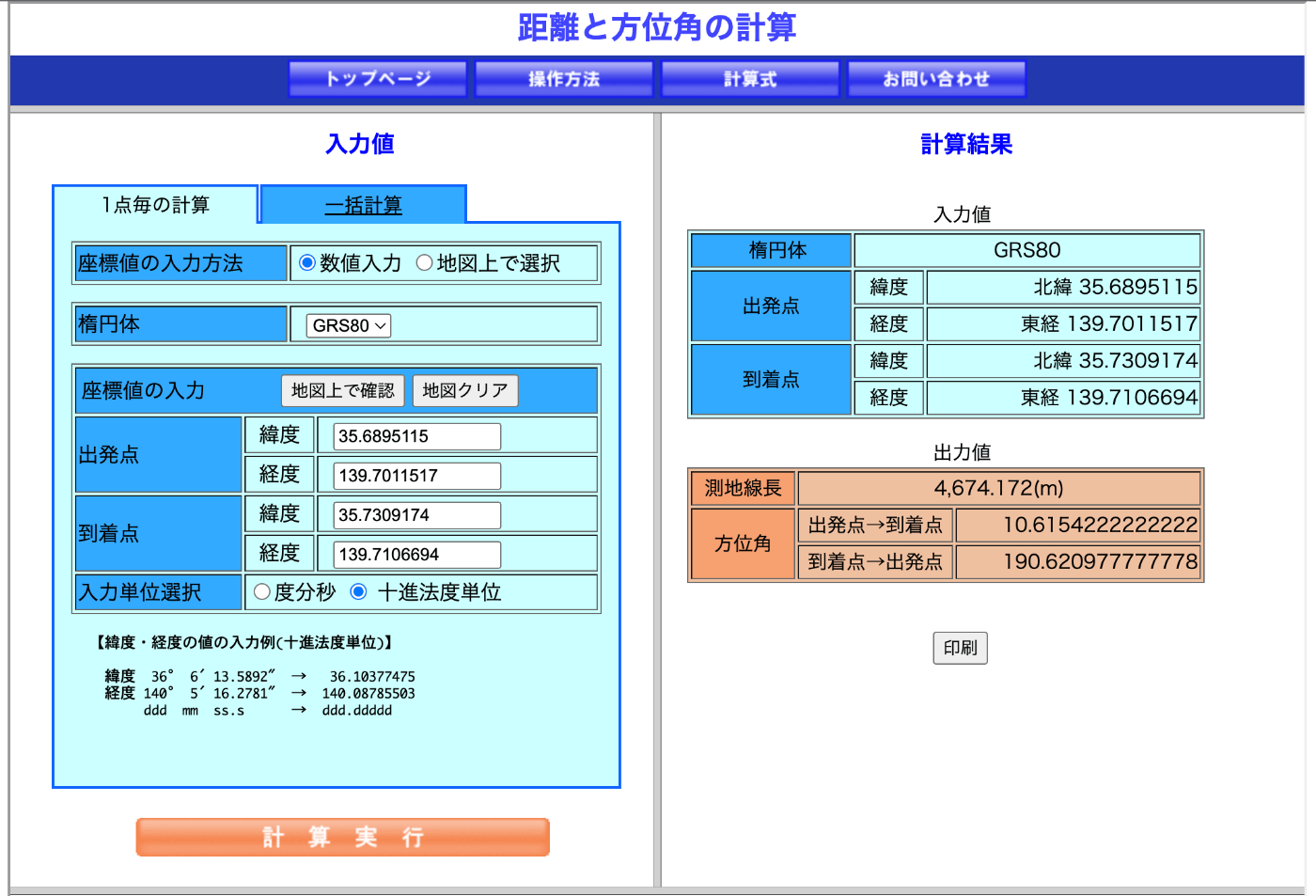
新宿駅-池袋駅間の距離(国土地理院)

ヒュベニ: 4674.17167754729
国土地理院: 4674.172

有効数字の範囲(mmオーダー)では誤差なく完全に一致しました。
まあ国土地理院の計算方法がわからないので実際のところはわかりませんが。

Excelで M×N

ここからは、これを $M \times N$ 個同時に計算していきます。

Excelにはスピルという機能があります。数式を1セルだけでなく範囲に対して適応していけるイメージです。

例えばA列1行に数字を入れおいて、B2セルに

=A2:A10 * B1:J1

という感じで書いておくと九九の表ができます。

今回は範囲が動的ですが、A:A * 1:1とかやると列も行も無限に計算してしまうのでOFFSET関数で範囲を指定します。最終列・行はCOUNT(A:A)という感じで取り出します。

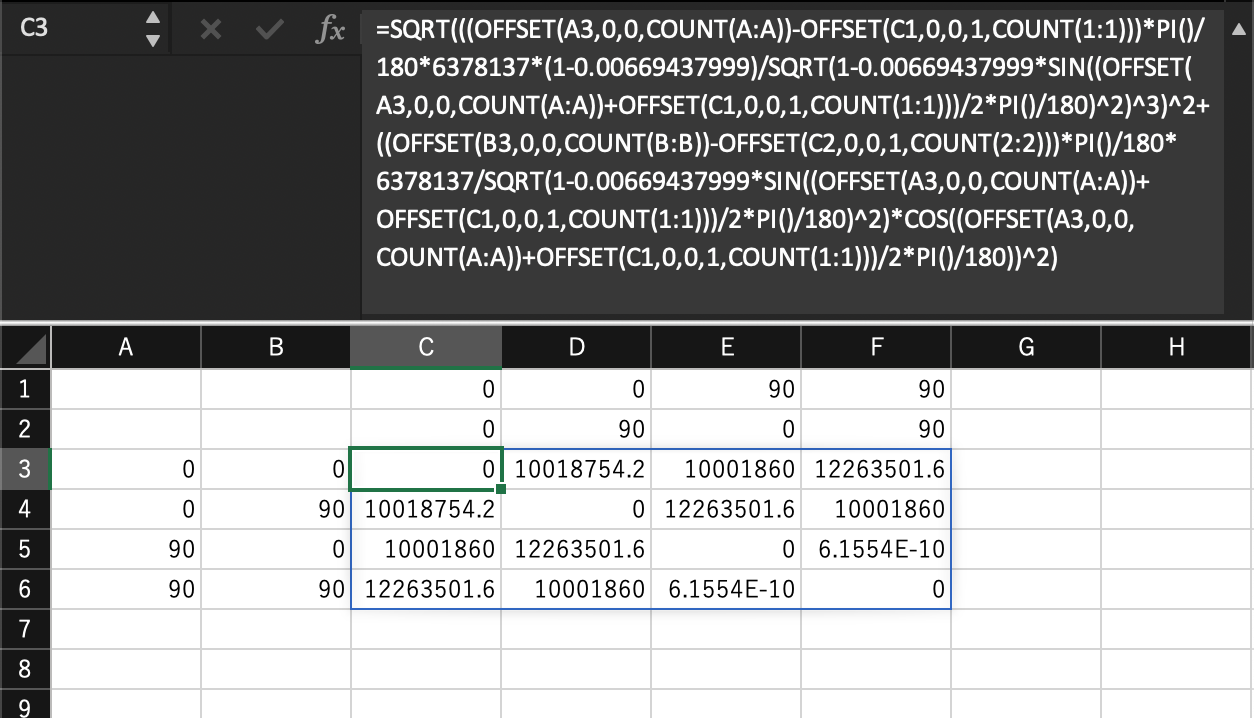
実装

=SQRT(((OFFSET(A3,0,0,COUNT(A:A))-OFFSET(C1,0,0,1,COUNT(1:1)))*PI()/180*6378137*(1-0.00669437999)/SQRT(1-0.00669437999*SIN((OFFSET(A3,0,0,COUNT(A:A))+OFFSET(C1,0,0,1,COUNT(1:1)))/2*PI()/180)^2)^3)^2+((OFFSET(B3,0,0,COUNT(B:B))-OFFSET(C2,0,0,1,COUNT(2:2)))*PI()/180*6378137/SQRT(1-0.00669437999*SIN((OFFSET(A3,0,0,COUNT(A:A))+OFFSET(C1,0,0,1,COUNT(1:1)))/2*PI()/180)^2)*COS((OFFSET(A3,0,0,COUNT(A:A))+OFFSET(C1,0,0,1,COUNT(1:1)))/2*PI()/180))^2)

Excelで M×N

Spreadsheetで M×N

同様の機能として、SpreadsheetにはARRAYFORMULA関数があります。これで任意の範囲に同じ数式を適用できます。

ただし、そのまま実装すると空欄の部分も計算してしまうので宇宙の果てまで計算が走って爆重になってしまいます。そのため、ARRAY_CONSTRAIN関数で計算範囲を限定してあげましょう。

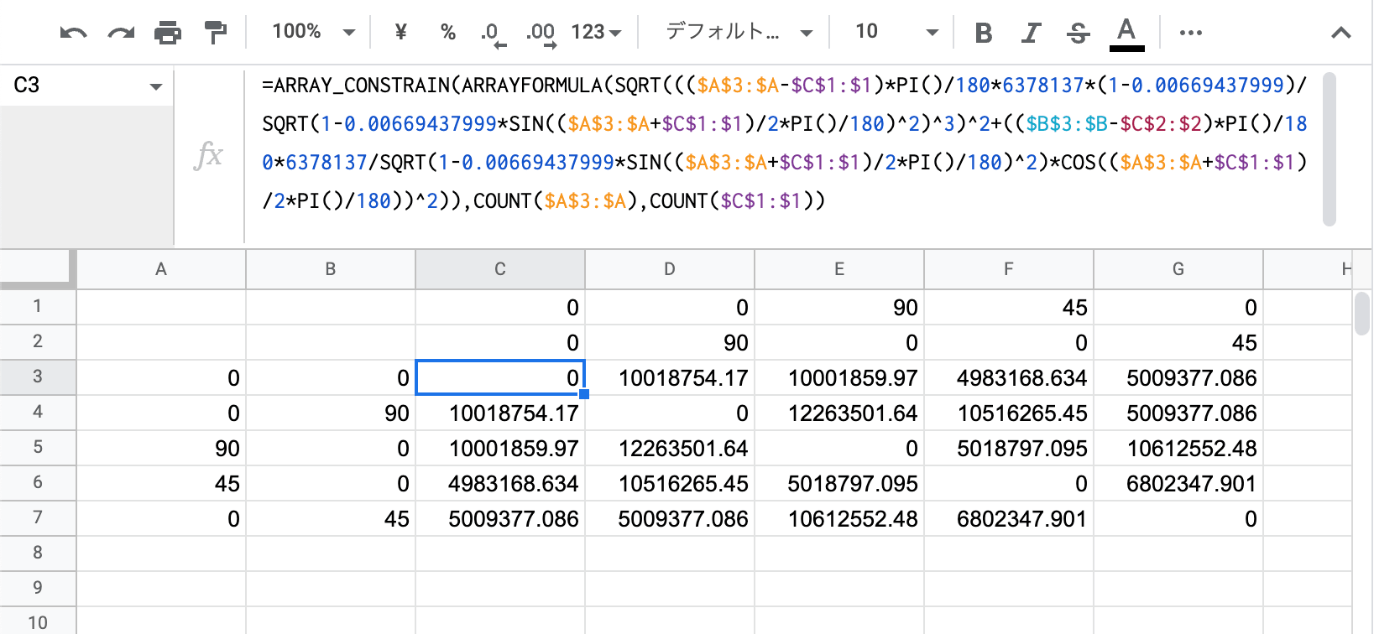
実装

=ARRAY_CONSTRAIN(ARRAYFORMULA(SQRT((($C$5:$C-$E$3:$3)*PI()/180*6378137*(1-0.00669437999)/SQRT(1-0.00669437999*SIN(($C$5:$C+$E$3:$3)/2*PI()/180)^2)^3)^2+(($D$5:$D-$E$4:$4)*PI()/180*6378137/SQRT(1-0.00669437999*SIN(($C$5:$C+$E$3:$3)/2*PI()/180)^2)*COS(($C$5:$C+$E$3:$3)/2*PI()/180))^2)),$A$4,$D$1)

Spreadsheetで M×N

まとめ

地球上の2点間の距離はヒュベニの公式がかなり実用的
- ただし日本くらいの緯度で、あまり遠くない(数十〜せいぜい数百kmくらい)
直積を一発で計算するには、Excelではスピル、SpreadsheetではARRAYFORMULAが便利
- 範囲はExcelではOFFSETで指定、SpreadsheetではARRAY_CONSTRAINTで指定すると良さそう
計算はめちゃくちゃ重いので1000点*1000点とかやるとフリーズするので注意

概要

ヒュベニの公式

2点間の距離

テスト

Excelで M×N

実装

Spreadsheetで M×N

実装

まとめ

Discussion