【テキスト分類】手を動かしてNaive Bayesを理解する
今回は、Naive Bayesに興味をもったため、テキスト分類を実装しつつ勉強してみました。
Naive Bayes
Naive Bayes はベイズの定理に基づく分類器で、「特徴が互いに条件付き独立である」という単純化(naive)仮定を置くことで、

という形で分類を行います。
つまり、以下のようなP(y|x)を計算して、一番大きいクラスに分類するということです。

変形すると、

右辺の分子はクラスyに関係なく一定なので、実際の計算では分子のみで比較することができます。
p(y)は、学習用データを数えてその割合を確率とします。
なお、プログラムにおいては、引数fit_prior=False とすることで、各クラスの確率は均一として計算することができます。
Bag-of-Words (BoW)
Bag-of-Words(BoW)は、テキストを「単語の出現頻度ベクトル」として表現する手法です。Naive Bayesでは、このBoWを用いてテキスト分類を行っていきます。
Bowの仕組み
- 語彙(ボキャブラリ)の構築
コーパス(全文章集合)から全ての異なる単語を抽出し、語彙一覧を作成する。
例えばコーパスに「猫が好き」「犬が好き」という文があれば、語彙は {「猫」「が」「好き」「犬」} となる。
- テキスト‐単語行列の作成
各テキストごとに語彙の各単語が何回出現したかをカウントし、ベクトル化する。
上記の例で「猫が好き」のベクトルは [1,1,1,0]、「犬が好き」は [0,1,1,1] となる。
BoWの弱点
- 語順・文脈情報の喪失
単語の出現順序や前後関係を全く考慮しないため、「犬が猫を追いかける」と「猫が犬を追いかける」を区別できない。
- 意味的な類似性を捉えられない
「走る」と「ジョギング」のように意味が近い単語を別物として扱うため、語彙が異なる同義語や類義語への対応が難しい。
- 未知語(OOV: Out-Of-Vocabulary)の問題
学習時に存在しなかった単語がテスト時に現れるとベクトルに反映できず、性能低下の原因となる。
使用したデータセット
BBCというニュースのテキストを5つのカテゴリに分類したものです。
データセット分割
今回は、事前にデータセットを学習用とテスト用に分割してみました。
以下はその際に使用したコードです。
import os
import shutil
import random
import argparse
def split_txt_files(src_dir, dst_dir_a, dst_dir_b, ratio=0.8, seed=None):
"""
指定したsrc_dir内の .txt ファイルを、与えられた比率(例: 0.8 は80%/20%)で
dst_dir_a と dst_dir_b の二つのディレクトリに分割コピーする関数。
パラメータ:
src_dir (str): .txt ファイルが格納されたソースディレクトリ
dst_dir_a (str): 第一グループ(例: 80%)のコピー先ディレクトリ
dst_dir_b (str): 第二グループ(例: 20%)のコピー先ディレクトリ
ratio (float): 分割比率(デフォルト: 0.8 は80%%/20%%)
seed (int, optional): 再現性のための乱数シード
"""
# 元ディレクトリが存在するか確認
if not os.path.isdir(src_dir):
raise NotADirectoryError(f"ソースディレクトリ '{src_dir}' が存在しません")
# コピー先ディレクトリを作成(存在しない場合)
os.makedirs(dst_dir_a, exist_ok=True)
os.makedirs(dst_dir_b, exist_ok=True)
# src_dir内の .txt ファイル一覧を取得
txt_files = [f for f in os.listdir(src_dir) if f.lower().endswith(".txt")]
if not txt_files:
print("ソースディレクトリに .txt ファイルが見つかりませんでした。")
return
# 乱数シードを設定(再現性のため)
if seed is not None:
random.seed(seed)
# ランダムにシャッフルして分割
random.shuffle(txt_files)
# 分割位置を算出
split_index = int(len(txt_files) * ratio)
# 80% と 20% に分割
group_a = txt_files[:split_index]
group_b = txt_files[split_index:]
# 各ディレクトリへコピー
for fname in group_a:
shutil.copy2(os.path.join(src_dir, fname), os.path.join(dst_dir_a, fname))
for fname in group_b:
shutil.copy2(os.path.join(src_dir, fname), os.path.join(dst_dir_b, fname))
# 結果を表示
print(f"合計ファイル数: {len(txt_files)} 件")
print(f"{len(group_a)} 件を '{dst_dir_a}' にコピーしました")
print(f"{len(group_b)} 件を '{dst_dir_b}' にコピーしました")
if __name__ == "__main__":
parser = argparse.ArgumentParser(
description="フォルダ内の .txt ファイルを指定した比率で二つのフォルダに分割コピーします。"
)
parser.add_argument("src_dir", help=".txt ファイルが格納されたソースディレクトリ")
parser.add_argument(
"dst_dir_a", help="第一グループ(例: 80%)のコピー先ディレクトリ"
)
parser.add_argument(
"dst_dir_b", help="第二グループ(例: 20%)のコピー先ディレクトリ"
)
parser.add_argument(
"--ratio",
type=float,
default=0.8,
help="分割比率(デフォルト: 0.8 は80%%/20%%)",
)
parser.add_argument(
"--seed", type=int, default=None, help="オプション: 再現性のための乱数シード"
)
args = parser.parse_args()
split_txt_files(args.src_dir, args.dst_dir_a, args.dst_dir_b, args.ratio, args.seed)
ディレクトリ構造
用意したデータのディレクトリ構造を以下に示します。
train_dir/
├── business/
│ ├── doc1.txt
│ ├── doc2.txt
│ └── ...
├── sports/
│ ├── docA.txt
│ └── ...
├── politics/
│ └── ...
├── technology/
│ └── ...
└── health/
└── ...
test_dir/
├── business/
│ ├── test1.txt
│ └── ...
├── sports/
│ └── ...
└── ...
BernoulliNB
概要
今回は、BernoulliNBとMultinomialNBの二種類のNaive Bayesを試します。
はじめに、BernoulliNBのコードを作成します。BernoulliNBは、単語が出現したかどうかのみを考慮するNaive Bayesです。同じ単語が複数回登場しても、その登場回数は考慮されません。
コード
import argparse
from pathlib import Path
from sklearn.datasets import load_files
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.naive_bayes import BernoulliNB
from sklearn.pipeline import Pipeline
from sklearn.metrics import classification_report, confusion_matrix
def parse_args():
parser = argparse.ArgumentParser(
description="Train and evaluate Naive Bayes with BoW on news data"
)
parser.add_argument(
"--train_dir",
type=Path,
required=True,
help="訓練用データのルートディレクトリ(カテゴリごとにサブフォルダ)",
)
parser.add_argument(
"--test_dir",
type=Path,
required=True,
help="テスト用データのルートディレクトリ(カテゴリごとにサブフォルダ)",
)
return parser.parse_args()
def main(train_dir: Path, test_dir: Path):
# データ読み込み: サブフォルダ名がラベルになる
print(f"Loading training data from {train_dir}")
train_data = load_files(str(train_dir), encoding="utf-8", decode_error="replace")
print(
f"Found {len(train_data.data)} documents in {len(train_data.target_names)} categories"
)
print(f"Loading test data from {test_dir}")
test_data = load_files(str(test_dir), encoding="utf-8", decode_error="replace")
print(
f"Found {len(test_data.data)} documents in {len(test_data.target_names)} categories"
)
# パイプラインの構築: BoW + MultinomialNB
pipeline = Pipeline(
[
("vect", CountVectorizer()), # Bag-of-Words ベクトル化
("clf", BernoulliNB()), # ナイーブベイズ分類器
]
)
# モデル学習
print("Training the model...")
pipeline.fit(train_data.data, train_data.target)
# テストデータで予測
print("Predicting on test data...")
preds = pipeline.predict(test_data.data)
# 評価結果表示
print("Classification Report:")
print(
classification_report(
test_data.target, preds, target_names=test_data.target_names
)
)
print("Confusion Matrix:")
print(confusion_matrix(test_data.target, preds))
if __name__ == "__main__":
args = parse_args()
main(args.train_dir, args.test_dir)
実行例
python bernoulli_nb.py --train_dir path/to/train_dir --test_dir path/to/test_dirp
MultinomialNB
概要
次に、MultinomialNBのコードを作成します。
MultinomialNBは、同じ単語が複数回登場した時にその登場回数を考慮することができます。
後述するラプラス平滑化を一旦無視して、以下のようなθ_yiを考えます。


訓練データにおいて同一単語が多く出現するほど、このθ_yiも大きくなります。これによって、訓練データにおける単語の登場回数を考慮することができます。
また、テストデータにおける条件付き確率は、以下の式で計算することができます。

テストデータにおいて、ある単語iの出現回数x_iとθ_yiをかけたものが加算されています。
つまり、単語iが多く出現するほど、logP(y|x)が増加します。
このような仕組みで、複数回登場する単語を考慮しています。
コード
import argparse
from pathlib import Path
from sklearn.datasets import load_files
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.pipeline import Pipeline
from sklearn.metrics import classification_report, confusion_matrix
def parse_args():
parser = argparse.ArgumentParser(
description="Train and evaluate Naive Bayes with BoW on news data"
)
parser.add_argument(
"--train_dir",
type=Path,
required=True,
help="訓練用データのルートディレクトリ(カテゴリごとにサブフォルダ)",
)
parser.add_argument(
"--test_dir",
type=Path,
required=True,
help="テスト用データのルートディレクトリ(カテゴリごとにサブフォルダ)",
)
return parser.parse_args()
def main(train_dir: Path, test_dir: Path):
# データ読み込み: サブフォルダ名がラベルになる
print(f"Loading training data from {train_dir}")
train_data = load_files(str(train_dir), encoding="utf-8", decode_error="replace")
print(
f"Found {len(train_data.data)} documents in {len(train_data.target_names)} categories"
)
print(f"Loading test data from {test_dir}")
test_data = load_files(str(test_dir), encoding="utf-8", decode_error="replace")
print(
f"Found {len(test_data.data)} documents in {len(test_data.target_names)} categories"
)
# パイプラインの構築: BoW + MultinomialNB
pipeline = Pipeline(
[
("vect", CountVectorizer()), # Bag-of-Words ベクトル化
("clf", MultinomialNB()), # ナイーブベイズ分類器
]
)
# モデル学習
print("Training the model...")
pipeline.fit(train_data.data, train_data.target)
# テストデータで予測
print("Predicting on test data...")
preds = pipeline.predict(test_data.data)
# 評価結果表示
print("Classification Report:")
print(
classification_report(
test_data.target, preds, target_names=test_data.target_names
)
)
print("Confusion Matrix:")
print(confusion_matrix(test_data.target, preds))
if __name__ == "__main__":
args = parse_args()
main(args.train_dir, args.test_dir)
実行例
python multinomial_nb.py --train_dir path/to/train_dir --test_dir path/to/test_dirp
結果の比較+考察
BernoulliNBの結果

MultinomialNBの結果
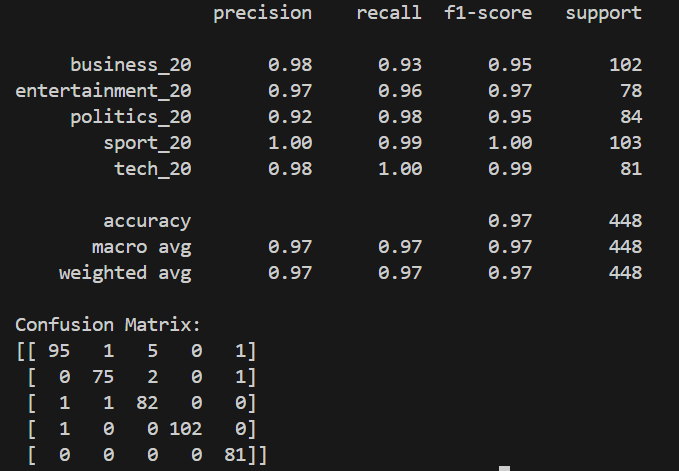
考察
- 全体精度(Accuracy)
- BernoulliNB: 0.96
- MultinomialNB: 0.97
MultinomialNB のほうが全体で約1ポイント高く、テキスト分類タスクでは発生回数を考慮できる MultinomialNB が有利に働いていると考えられる。
- クラス別 F1スコア
| クラス | BernoulliNB F1 | MultinomialNB F1 |
|---|---|---|
| business | 0.93 | 0.95 |
| entertainment | 0.96 | 0.97 |
| politics | 0.93 | 0.95 |
| sport | 1.00 | 1.00 |
| tech | 0.97 | 0.99 |
すべてのクラスで MultinomialNB の F1 スコアが BernoulliNB を上回っている、または同等。
- 混同行列
混同行列は行が「実際のクラス」、列が「予測したクラス」を表しています。
例えば、BernoulliNBの行0列0の値100は、「実際にクラス0のデータを、モデルもクラス0と正しく予測した件数」です。
対して、BernoulliNBの行2列0の値7は、「実際にはクラス2のデータを、モデルがクラス0と誤って予測した件数」です。
BernoulliNB: MultinomialNB:
[[100 0 2 0 0] [[ 95 1 5 0 1]
[ 2 75 1 0 0] [ 0 75 2 0 1]
[ 7 1 76 0 0] [ 1 1 82 0 0]
[ 1 0 0 102 0] [ 1 0 0 102 0]
[ 2 3 0 0 76]] [ 0 0 0 0 81]]
・BernoulliNBではpolitics → business の誤分類が7件と多め。
・MultinomialNBでは、politics→business の誤分類が大幅に改善したが、business → politics が5件に増加した。
結果全体をを見ると、MultinomialNBのほうが性能が良いと言えそうです。
ラプラス平滑
最後に、先ほどは無視して考えていたラプラス平滑について簡単にまとめてみます。
学習データに出現しなかった単語に関しては、先ほど考えたθ_yiが0になってしまいます。


そうなると、log(θ_yi)を計算する際に、log(θ_yi) = -∞ となってしまいます。

以下の式で考えるともっとわかりやすいと思います。

学習データに出現しなかった単語jがテストデータに出現した場合、事前確率P(x|y)=0となります。すると、他の単語が何であろうと、事後確率P(y|x)=0になってしまいます。
これでは分類を行うことができません。
この現象に対処するために、未出現単語にも確率質量を割り当てる手法がラプラス平滑です。
通常α=1として、以下のように置きます。

この場合、学習データに一度も出現しなかった単語がテストデータに出現したとしても、θ_yiは0+α≠0 となるため、先ほどの問題を解決できるというわけです。
おわりに
今回は、Naive Bayesによるテキスト分類について、コードを動かしつつ勉強してみました。今後も機械学習の内容を勉強しながら記事を書いていくつもりです。
最後までお読みいただき、誠にありがとうございました!
Discussion