✂️
ベイズでLOOCV (Leave-One-Out Cross-Validation)

2025/02/17に公開
Python
PyMCの使い方を調べていたらArviZにlooというAPIがあるのを見つけました。どうやらleave-one-out cross-validation (LOOCV) を使ってELPDを推定してくれるみたいです。LOOCVといえばデータセットの分割数をデータ数と同じまで細分化した究極のクロスバリデーションで、計算量の多さから机上の空論だとずっと思っていました。本当に動くのでしょうか……？
そこでドキュメントで引用されている論文をたどりlooがどのようにLOOCVを計算するのか調べてみたところ、そもそもベイズモデルは1回学習させるだけでクロスバリデーションを行えることがわかりました。言われてみれば当たり前のことなのですが私はなかなか気づけなかったので、備忘録も兼ねて調べた内容をここにまとめておこうと思います。

 ベースとなるアイデア学習データの説明変数を X = \{x_1, x_2, \cdots x_N\} 、目的変数を Y = \{y_1, y_2, \cdots y_N\} 、パラメーターを \theta とおきます。各データ点が独立同分布に従うと仮定すると、パラメーターの事後分布は各データ点の尤度の積で表すことができます。

p(\theta \mid Y, X)
\propto p(Y \mid X, \theta) p(\theta)
= p(y_1 \mid x_1, \theta) p(y_2 \mid x_2, \theta) \cdots p(y_N \mid x_N, \theta) p(\theta)
同様に、n 番目のデータ点を除いて作ったデータ \{Y_{-n}, X_{-n}\} で学習させたパラメーターの事後分布は n 番目のデータ点以外の尤度の積で表すことができます。そして、n 番目のデータ点以外の尤度の積は全データ点の尤度の積を n 番目のデータ点の尤度で割ることで求められます。

p(\theta \mid Y_{-n}, X_{-n}) \propto \frac{p(\theta \mid Y, X)}{p(y_n \mid x_n, \theta)}
この結果は、事後分布を特定の学習データの尤度で割ることにより、その学習データを学習済みベイズモデルから「忘却」させられることを意味します (※忘却という言葉は本記事で便宜的に定義したものであり、専門用語ではありません)。したがって、ベイズモデルのクロスバリデーションでは各foldで学習をやり直す代わりにOOFを忘却させるというアプローチを取ることができます。忘却は尤度で割るだけですから、学習よりも計算量が少なくなることが期待されます。

 素朴なCV手法｜IS-LOOCVでは実際に忘却を用いたクロスバリデーションを組み立てていきましょう。ここでは学習データの分割数をデータ数と等しくしたクロスバリデーションであるleave-one-out cross-validation (LOOCV) を、MCMCを使って近似的に行うことを考えます。
なお、LOOCVの式の導出は "Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC" の第2章を、重点サンプリングによるLOOCVの近似計算は "Pattern Recognition and Machine Learning" の第11章を参考にしました。

 導出まず、学習データをすべて使ってパラメーターの事後分布を求めます。

p(\theta \mid Y, X)
そしてそれをOOFの尤度で割り、各foldのパラメーターの事後分布を求めます。ここが冒頭に触れた、学習の代わりに忘却を用いる話に対応します。

p(\theta \mid Y_{-n}, X_{-n}) \propto \frac{p(\theta \mid Y, X)}{p(y_n \mid x_n, \theta)}
次に、生成分布を事後分布で周辺化し予測分布を求めます。

\begin{aligned}
p(y_n^{\text{pred}} \mid x_n, Y_{-n}, X_{-n})
&= \int{p(y_n^{\text{pred}} \mid x_n, \theta) p(\theta \mid Y_{-n}, X_{-n}) \ d\theta} \\
&= \frac{1}{Z_n} \int{p(y_n^{\text{pred}} \mid x_n, \theta) \frac{p(\theta \mid Y, X)}{p(y_n \mid x_n, \theta)} \ d\theta} \\
&= \frac{1}{Z_n} \int{\frac{p(y_n^{\text{pred}}, \theta \mid x_n, Y, X)}{p(y_n \mid x_n, \theta)} \ d\theta}
\end{aligned}
ただし、Z_n は予測分布を0～1に収めるための正規化定数です。

Z_n = \iint{\frac{p(y_n^{\text{pred}}, \theta \mid x_n, Y, X)}{p(y_n \mid x_n, \theta)} \ d\theta \ d y_n^{\text{pred}}}
最後に、予測分布を用いて各foldの損失の期待値を求めそれらの平均を取ればLOOCVの完成です。各OOFの損失を求める関数を l(y^{\text{true}}, y^{\text{pred}}) とおくと、LOOCVは以下のようになります。

\begin{aligned}
\text{LOOCV}
&= \frac{1}{N} \sum_{n=1}^{N} \left[ \int{l(y_n, y_n^{\text{pred}}) p(y_n^{\text{pred}} \mid x_n, Y_{-n}, X_{-n}) \ dy_n^{\text{pred}}} \right] \\
&= \frac{1}{N} \sum_{n=1}^{N} \left[ \int{l(y_n, y_n^{\text{pred}}) \left( \frac{1}{Z_n} \int{\frac{p(y_n^{\text{pred}}, \theta \mid x_n, Y, X)}{p(y_n \mid x_n, \theta)} \ d\theta} \right) \ dy_n^{\text{pred}}} \right]
\end{aligned}

 MCMCによる近似LOOCVの式を導出することはできましたが、パラメーターと目的変数との二重積分が含まれており解析的に計算するのは大変そうですね。そこで、MCMCを使って近似的に計算することにしましょう。事後分布 p(y_n^{\text{pred}}, \theta \mid x_n, Y, X) からのMCMCサンプル \{y_{n,s}^{\text{pred}}, \theta_s \mid s \in [1, \cdots, S]\} が得られていると仮定して話を進めます。
まず準備として、尤度の逆数を r とおきます。MCMCによるLOOCVの近似は実は重点サンプリングになっており、r は重要度重みに相当します。具体的には、目的の p(y_n^{\text{pred}}, \theta \mid x_n, Y_{-n}, X_{-n}) からサンプリングする代わりに p(y_n^{\text{pred}}, \theta \mid x_n, Y, X) からサンプリングし得られたMCMCサンプルを重要度重み r で重み付けして期待値を計算している、と捉えることができます。

\begin{aligned}
r_{n,s}
&= \frac{1}{p(y_n \mid x_n, \theta_s)} \\
&= \frac{{p(y_{n,s}^{\text{pred}}, \theta_s \mid x_n, Y, X)} \mathop{/} {p(y_n \mid x_n, \theta_s)}}{p(y_{n,s}^{\text{pred}}, \theta_s \mid x_n, Y, X)} \\
&\propto \frac{p(y_{n,s}^{\text{pred}}, \theta_s \mid x_n, Y_{-n}, X_{-n})}{p(y_{n,s}^{\text{pred}}, \theta_s \mid x_n, Y, X)}
\end{aligned}
では、LOOCVを近似していきましょう。LOOCVの式を少し変形すると p(y_n^{\text{pred}}, \theta \mid x_n, Y, X) での期待値になっていることがわかります。したがって、p(y_n^{\text{pred}}, \theta \mid x_n, Y, X) からサンプリングしたMCMCサンプルの平均で近似できます。

\begin{aligned}
\text{LOOCV}
&= \frac{1}{N} \sum_{n=1}^{N} \left[ \int{l(y_n, y_n^{\text{pred}}) \left( \frac{1}{Z_n} \int{\frac{p(y_n^{\text{pred}}, \theta \mid x_n, Y, X)}{p(y_n \mid x_n, \theta)} \ d\theta} \right) \ dy_n^{\text{pred}}} \right] \\
&= \frac{1}{N} \sum_{n=1}^{N} \left[ \frac{1}{Z_n} \iint{ \left\{ \frac{1}{p(y_n \mid x_n, \theta)} l(y_n, y_n^{\text{pred}}) \right\} p(y_n^{\text{pred}}, \theta \mid x_n, Y, X) \ d\theta \ dy_n^{\text{pred}}} \right] \\
&\fallingdotseq \frac{1}{N} \sum_{n=1}^{N} \left[ \frac{1}{Z_n} \frac{1}{S} \sum_{s=1}^{S}{r_{n,s} l(y_n, y_{n,s}^{\text{pred}})} \right]
\end{aligned}
正規化定数 Z_n も同様です。

\begin{aligned}
Z_n
&= \iint{\frac{p(y_n^{\text{pred}}, \theta \mid x_n, Y, X)}{p(y_n \mid x_n, \theta)} \ d\theta \ d y_n^{\text{pred}}} \\
&= \iint{\frac{1}{p(y_n \mid x_n, \theta)} p(y_n^{\text{pred}}, \theta \mid x_n, Y, X) \ d\theta \ d y_n^{\text{pred}}} \\
&\fallingdotseq \frac{1}{S} \sum_{s=1}^{S}{r_{n,s}}
\end{aligned}
これらの結果をまとめると、LOOCVは損失 l(y_n, y_{n,s}^{\text{pred}}) を正規化された重要度重み r_{n,s} \mathop{/} \sum_{s=1}^{S}{r_{n,s}} で重み付けして平均を取れば計算できることがわかります。

\begin{aligned}
\text{LOOCV}
&\fallingdotseq  \frac{1}{N} \sum_{n=1}^{N} \left[ \frac{\frac{1}{S} \sum_{s=1}^{S}{r_{n,s} l(y_n, y_{n,s}^{\text{pred}})}}{\frac{1}{S} \sum_{s=1}^{S}{r_{n,s}}} \right] \\
&= \frac{1}{N} \sum_{n=1}^{N} \left[ \sum_{s=1}^{S}{\frac{r_{n,s}}{\sum_{s=1}^{S}{r_{n,s}}} l(y_n, y_{n,s}^{\text{pred}})} \right]
\end{aligned}
以上の方法は、LOOCVを重点サンプリングで計算することからimportance sampling leave-one-out cross-validation (IS-LOOCV) と呼ばれています。

 問題点手軽にLOOCVを実現できるIS-LOOCVですが、実は問題があります。それは重要度重みが尤度の逆数だということです。尤度は非常に小さな値を取る可能性があるため、その逆数である重要度重みは非常に大きな値を取る可能性があります。特に尤度関数が裾の重い形状をしている場合、そのような重要度重みがサンプリングされやすいため期待値計算が不安定になってしまうのです。この問題を緩和するために提案されたのが、次に紹介するPareto smoothed importance samplingです。

 安定化させたCV手法｜PSIS-LOOCVここからは、IS-LOOCVの不安定さを緩和する手法としてのPareto Smoothed Importance Sampling (PSIS) をベイズ線形回帰モデルを例に見ていきます。なお、LOOCVへの適用をかなり意識してはいるものの、PSIS自体は重点サンプリングを用いた期待値計算を安定化させるための汎用的な手法です。
モジュールの読み込みimport numpy as np
import pandas as pd
from scipy import stats
import pymc as pm
import arviz as az
from matplotlib import pyplot as plt
import seaborn as sns

 事例の設定PSISを説明するための例として、y = 2 x - 10 + e という回帰問題を扱います。e はノイズで、自由度3のt分布に従うものと設定しました。t分布は裾が重いので、ときどき大きなノイズが生じます (以下の例だと x \fallingdotseq 1 の点が該当)。
データ生成random_state = np.random.RandomState(2)
size = 10
coef_true = 2.0
intercept_true = -10
df_true = 3.0
sigma_true = 1.0
x = np.linspace(start=0, stop=10, num=size)
y = coef_true * x + intercept_true + random_state.standard_t(df=df_true, size=size) * sigma_true

plt.scatter(x, y, color='C0')
plt.plot(x, coef_true * x + intercept_true, color='C0')
plt.xlabel('x')
plt.ylabel('y')
plt.xlim(0, 10)
plt.ylim(-20, 20)
plt.show()

 モデル特定と推論一方で、モデルではノイズが正規分布に従うと仮定します。真のモデルではノイズはt分布に従うので、モデルが誤特定されている状態になっています。
モデル特定with pm.Model(coords = {'index': range(size)}) as model:
    coef = pm.Normal('coef', mu=0.0, sigma=10.0)
    intercept = pm.Normal('intercept', mu=0.0, sigma=10.0)
    sigma = pm.HalfCauchy('sigma', beta=10.0)
    y_pred = pm.Normal('y', mu = coef * x + intercept, sigma=sigma, observed=y, dims='index')

pm.model_to_graphviz(model)
MCMCを使って実際に推論してみると、分散を大きめに取って x \fallingdotseq 1 の点を何とかカバーしようとしていることがわかります。この点の尤度は非常に小さな値になることから、その逆数である重要度重みは非常に大きな値になり期待値の計算を不安定にさせる可能性があります。
推論with model:
    idata = pm.sample(1000, nuts_sampler='numpyro', idata_kwargs = {"log_likelihood": True}, random_seed=0)
    idata.extend(pm.sample_posterior_predictive(idata, random_seed=0))

az.plot_hdi(x, idata.posterior_predictive['y'], color='C1')
plt.plot(x, idata.posterior_predictive['y'].mean(['chain', 'draw']), color='C1', label='pred')
plt.scatter(x, y, color='C0')
plt.plot(x, coef_true * x + intercept_true, color='C0', label='true')
plt.xlabel('x')
plt.ylabel('y')
plt.xlim(0, 10)
plt.ylim(-20, 20)
plt.legend()
plt.show()

 重要度重みの分布ここで、各点の重要度重みの分布を見てみましょう。予想通り x \fallingdotseq 1 の点 (オレンジ色) だけ取りうる値の範囲が広く、非常に大きな値を取る可能性があることがわかります。特に注目すべきは r = 10^6 付近に存在する孤立したピークです。これは、確率密度の低い領域からたまたまサンプリングされた点の出現頻度が、MCMCサンプルのサイズが十分でないせいで本来の確率密度よりも高くなっていることを表しています。非常に大きな重要度重みが本来の確率密度より高い出現頻度で期待値計算に組み込まれることになり、計算された期待値が真の値からずれてしまうわけです。
重要度重みの算出for n in range(size):
    log_likelihood = idata.log_likelihood['y'].stack(__sample__ = ['chain', 'draw'])[n, :].to_numpy()
    r = 1 / np.exp(log_likelihood)
    kde = stats.gaussian_kde(r)

    r_ = 10 ** np.linspace(-2, 12, 10000)
    plt.plot(r_, kde(r_), label=n)

plt.xscale('log')
plt.yscale('log')
plt.xlim(1e-2, 1e8)
plt.ylim(1e-20, 1e-0)
plt.xlabel('r')
plt.ylabel('確率密度')
plt.legend(title='n')
plt.show()

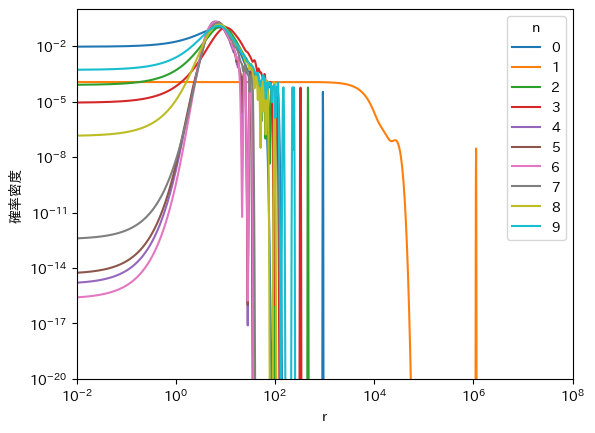
 PSISによるMCMCサンプルの修正この問題を緩和するため、右裾からサンプリングされた点を修正することを考えます。ナイーブな案としては右裾からサンプリングされた点を捨ててしまう方法が考えられますが、それだと重要度重みの分布を途中で打ち切っていることになり期待値にバイアスが生じてしまいます。
そこでPSISでは、累積分布関数の逆関数が既知の分布で右裾を近似し、その近似分布から均等にサンプリングしなおして問題のある点を置き換えることでMCMCサンプルを修正します。累積分布関数の逆関数が既知の分布で近似するのは、たとえば10個の点をサンプリングする場合なら下側確率が 0.05、0.15、...、0.95 のときの確率変数の値を逆関数で求めれば均等なサンプルを得られるからです。近似分布には、確率分布の裾を近似する際によく用いられる (……とWikipediaに書いてある。へー) 一般化パレート分布を用います。これが Pareto smoothed importance sampling という名前の由来になっています。
では実際に、PSISで重要度重みをサンプリングしなおしてみましょう。灰色の点線より右側がPSISによる修正対象の領域になっており、オレンジ色の線が一般化パレート分布による裾の近似分布、緑色の線が近似分布の累積分布関数、緑色の点が近似分布から均等にサンプリングしなおした新しいサンプルです (※ここではわかりやすさのために10個だけサンプリングしていますが、本来のPSISでは灰色の点線より右側にある点と同じ数だけサンプリングします)。近似分布から均等にサンプリングしなおしたおかげで、元のMCMCサンプルにあった r = 10^6 のような非常に大きな値を取る重要度重みが含まれなくなりました。
PSISn = 1  # 外れ値の添え字
log_likelihood = idata.log_likelihood['y'].stack(__sample__ = ['chain', 'draw'])[n, :].to_numpy()
r = 1 / np.exp(log_likelihood)
kde = stats.gaussian_kde(r)

from arviz.stats.stats import _gpdfit  # (注意) 検証のために公開されていない関数を承知の上で読み込んで利用しています。常用はしないでください。
S = len(r)
M = int(min(0.2 * S, 3 * np.sqrt(S)))
r_tail = np.sort(r)[-M:]
gp_k, gp_sigma = _gpdfit(r_tail)
gpd_pdf = lambda r: stats.genpareto.pdf(r, c=gp_k, loc=np.min(r_tail), scale=gp_sigma)
gpd_cdf = lambda r: stats.genpareto.cdf(r, c=gp_k, loc=np.min(r_tail), scale=gp_sigma)
tail_ratio = kde.integrate_box_1d(np.min(r_tail), np.inf)

z = np.arange(1, 10 + 1)  # z = np.arange(1, M + 1)
c_w = (z - 0.5) / 10  # c_w = (z - 0.5) / M
w = stats.genpareto.ppf(c_w, c=gp_k, loc = np.min(r_tail), scale=gp_sigma)

r_ = 10 ** np.linspace(-2, 12, 10000)
r_tail_ = r_[r_ >= np.min(r_tail)]
plt.plot(r_, kde(r_), label='(左軸) MCMCサンプルの分布')
plt.plot(r_tail_, gpd_pdf(r_tail_) * tail_ratio, color='C1', label='(左軸) 一般化パレート分布による裾の近似分布')
plt.axvline(np.min(r_tail), color='gray', linestyle=':')
plt.xscale('log')
plt.yscale('log')
plt.xlim(1e-2, 1e12)
plt.ylim(1e-20, 1e-2)
plt.xlabel('r')
plt.ylabel('確率密度')
h1, l1 = plt.gca().get_legend_handles_labels()
plt.twinx()
plt.plot(r_tail_, gpd_cdf(r_tail_), color='C2', label='(右軸) 近似分布の累積分布関数')
plt.scatter(w, c_w, color='C2', label='(右軸) 近似分布から均等にサンプリングした裾の新しいサンプル')
h2, l2 = plt.gca().get_legend_handles_labels()
plt.ylabel('下側確率')
plt.legend(h1 + h2, l1 + l2, bbox_to_anchor=(0, 1), loc='lower left')
plt.show()

 ArviZでのPSIS-LOOCVの実装最後に、PSIS-LOOCVの実装方法を確認しておきましょう。Rなら論文著者らによるlooパッケージが、PythonならArviZのpsislwなどが使えます。たとえばRMSEであれば、ArviZのpsislwを使って以下のように実装できます。
def rmse(y_true, y_pred, log_weights):
    from scipy.special import logsumexp
    log_se_n_s = np.log((y_true[:, np.newaxis] - y_pred) ** 2)
    log_se_n = logsumexp(log_se_n_s + log_weights, axis=1) - logsumexp(log_weights, axis=1)
    log_se = logsumexp(log_se_n) - np.log(len(y_true))
    return np.sqrt(np.exp(log_se))

# log_weights = -log_likelihood  # ISの場合
log_weights, pareto_shape = az.psislw(-log_likelihood)  # PSISの場合
rmse(y_true, y_pred, log_weights)
実際にRMSEを計算してみると以下のようになります。青色がISで、オレンジ色がPSISで、緑色が真の分布から計算したRMSEです。基本的にはISでもPSISでもほぼ同じ値を取りつつ、たとえば x \fallingdotseq 1 の点 (左から2番目の、n=1の棒グラフ) を見るとISで高めに出ていた値がPSISで低めに修正され真のRMSEに近づいていることがわかります。
RMSEの比較y_true = idata.observed_data['y'].to_numpy()
y_pred = idata.posterior_predictive['y'].stack(__sample__ = ["chain", "draw"]).to_numpy()
log_likelihood = idata.log_likelihood['y'].stack(__sample__ = ["chain", "draw"]).to_numpy()

# IS-LOOCV RMSE
log_weights = -log_likelihood
is_rmse_n = [rmse(y_true[[n]], y_pred[[n], :], log_weights[[n], :]) for n in range(size)] + [rmse(y_true, y_pred, log_weights)]
# PSIS-LOOCV RMSE
log_weights, pareto_shape = az.psislw(-log_likelihood)
psis_rmse_n = [rmse(y_true[[n]], y_pred[[n], :], log_weights[[n], :]) for n in range(size)] + [rmse(y_true, y_pred, log_weights)]

# 真の分布から計算したRMSE
with pm.Model(coords = {'index': range(size)}) as model_true:
    pm.StudentT('y', nu=df_true, mu = coef_true * x + intercept_true, sigma=sigma_true, dims='index')
    idata_true = pm.sample_prior_predictive(100000, random_seed=0)
y_true = y
y_pred = idata_true.prior['y'].stack(__sample__ = ["chain", "draw"]).to_numpy()
log_weights = np.full(y_pred.shape, -np.log(y_pred.shape[1]))
rmse(y_true, y_pred, log_weights)
true_rmse_n = [rmse(y_true[[n]], y_pred[[n], :], log_weights[[n], :]) for n in range(size)] + [rmse(y_true, y_pred, log_weights)]

plt.figure(figsize = (12, 4))
sns.barplot(
    data = (
        pd.DataFrame({
            'n': [str(n) for n in range(size)] + ['Total'],
            'IS': is_rmse_n,
            'PSIS': psis_rmse_n,
            'Truth': true_rmse_n
        })
        .melt(id_vars='n', var_name='method', value_name='rmse')
    ),
    x='n',
    y='rmse',
    hue='method'
)
plt.ylabel('RMSE')
plt.show()

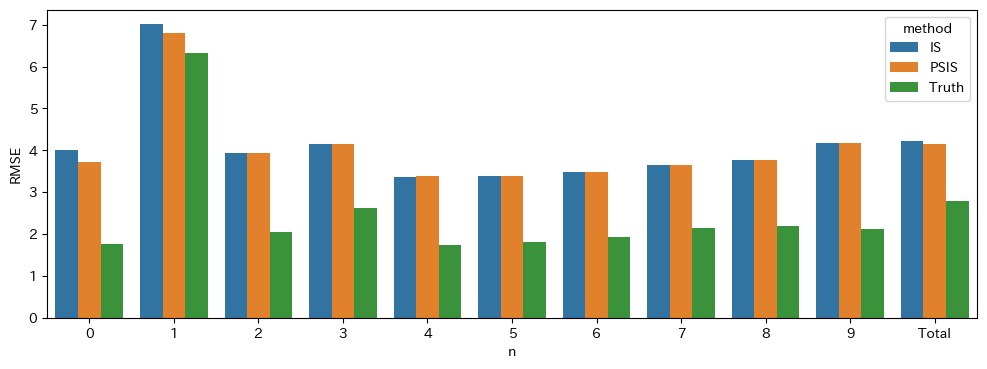
 本記事で触れられなかったこと本記事では期待値計算の安定性を高める仕組みに重点を置いてPSISを解説しました。しかし、期待値計算の安定化はPSISが実現したかったことの一部に過ぎません。論文ではPSISを使ってMCMCによる近似がうまくいっているか診断することや目標の近似精度を得るために必要なサンプルサイズを見積もることを提案しており、そういった実践的な機能を提供できる点がWAICなどの競合する汎化誤差の推定手法との差別化要素となっているのです。ただ、これらの機能は極値理論にもとづいており私の理解を超えるため本記事では割愛しました。興味がある方はぜひ原著論文を読んでみてください。
また、汎化誤差の推定手法としてはPSIS-LOOCVよりもWAICのほうが優れているという指摘があります。過去にはWAICの発案者である渡辺先生自らによる解説が渡辺先生のホームページにあったようなのですが、ご退官に伴いホームページが削除され読めなくなってしまいました (悲しい……)。理論的な話はさておき、経験的には松浦さんによる比較実験 (情報量規準LOOCVとWAICの比較) などでWAICのほうが優れていることが示されています。

 参考文献
Pareto Smoothed Importance Sampling
本記事で解説した論文。本記事の内容は論文の第1章と第2章に相当します。


Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC
IS-LOOCVを理解するため主に第2章を参照しました。


Pattern Recognition and Machine Learning
IS-LOOCVのベースである重点サンプリングを理解するため主に11.1.4を参照しました。


情報量規準LOOCVとWAICの比較
PSIS-LOOCVとWAICの比較実験。真の汎化誤差を計算可能な人工データを複数パターン作り、真の汎化誤差により近い推定値を得られる手法や条件を調べている。