🔁

モンテカルロ・シミュレーションの並列実行における乱数生成の再現性担保について

Yamaguchi Ryusei

2025/10/01に公開

 1. はじめに金融機関の信用リスク管理においては、モンテカルロ・シミュレーションによる乱数生成を用いたリスク量計測を行うことがあります。例えば、与信ポートフォリオにおける信用リスク量の計測（VaRやUL）が挙げられ、この場合は与信先のデフォルトによる損失分布を計算するために利用しています。
多くの場合、与信ポートフォリオの損失分布を計算する際は、以下の状況が考えられます。
VaR（損失分布の裾野）を正確に計測するために、シミュレーション回数をかなり大きく設定する必要がある
与信先の件数が多い（=ポートフォリオが大きい）ために計算負荷が重く、１回あたりの処理の計算時間がかかる
従って、２重に計算時間がかかることになり、一般的には並列処理によって高速化を試みています。モンテカルロ・シミュレーションは同一処理を繰り返すという点で並列処理と相性が良いですが、一方で、シミュレーション結果における再現性の担保の重要な要素であり、計算結果の適切さを遡って確認できる状況であることが求められます。
この2つの要素（並列処理による高速化＋乱数の再現性担保）をどのように達成するかが課題であり、本記事では同一シード上での乱数生成数の規模が大きいモンテカルロ・シミュレーションについて、特に並列処理を行う上での実験再現性の担保を検討した内容についてご紹介いたします。

 1.1 各種設定なお、実験環境で扱うライブラリのバージョンは以下の通りです。
Python 3.12.5
numpy 2.3.0
scipy 1.15.3
joblib 1.5.1
また、疑似乱数生成器として本記事では断りがない場合は全てPCG64を用います。詳細はこちらをご覧ください。

https://www.pcg-random.org/

 1.2 キーポイントの整理本記事のポイントをまとめておきます。各観点の込み入った部分については各章をご覧ください。

 【2章】再現性担保のために必要な概念について乱数は疑似乱数生成器による規則的な整数値を順に用いて発生させている。
特定の分布の乱数を生成する際に棄却採択法のアルゴリズムが採用されている場合、乱数の生成数と内部状態の進行速度が一致しない。
並列処理において、各コアごとに段階を進めた疑似乱数生成器を渡す必要があるが、PCG64は任意の数だけ内部状態を進めることが可能。
生成したい乱数の分布によっては、生成したい乱数の数よりも多く内部状態を進める必要がある。
再現性を担保する上では、１コア当たりのシミュレーション回数を固定しておく必要がある。

 【3・4章】具体的な実装方法と簡易検証乱数生成のためのベース準備
np.random.Generator(np.random.PCG64(seed=42))

並列処理を行う前に、予め内部状態を進めておく
np.random.PCG64.advance()
※発生したい分布によっては作成したい乱数よりも多く進めておく

2章で解説している注意点について、簡易検証としてシミュレーションを行い、その様子を確認

 【5章】補足情報乱数の生成結果の保存は、csvよりも型レベルで保存できる形式を用いることが望ましい
scipyライブラリで乱数を発生させる際もGeneratorを用いることが可能

 2. 再現性担保のために必要な概念について本章では、同一シード下における並列処理での乱数の再現性担保のために必要な概念について紹介します。

 2.1. ある分布の乱数を生成するイメージの理解はじめに特定の分布の乱数がどのように作成されるかのイメージを掴みます。実際にはここまで単純ではないのですが、標題の目標を達成するに必要な理解はそこまで深くなくても良いため、簡略化したもので解説します。
乱数は、擬似乱数生成器(以下、PRNG)から生成されるビット整数値(以下、state)を使って、これを分布変換することによって生成されます。乱数を発生させると、PRNGの内部状態が進み新しいstateが生成されるため、次の乱数ははまた異なるものが得られます。また、PRNGは初期値を与えることで一定の周期を持つ確定的な値の連鎖を作成します。「メルセンヌツイスター」や「PCG」はこのPRNGを生成するためのアルゴリズムの名称になります。これにより、擬似的にランダムな値が出るような状況を作ることができます。
!上記で定義するstateと、一般に分布生成の元として使用される整数値は厳密には異なるものとなりますが、本記事においては簡略化としてあまり切り分けずに同一視することとします。そのため、イメージとして元となる整数値が順に並んでいていて、それを基に乱数が生成されるということが分かれば、以降もそれほど問題なく解釈できるかと思います。

 2.2. 乱数の生成結果の固定前節を踏まえてここで抑えておきたい重要なポイントは、擬似乱数生成器から生成されるstateを常に同じ状態を再現して使うことができるのであれば、乱数はいつも同じ値が返ってくるということです。そのため普段何気なくやっているシードの固定という操作は、PRNGの初期値の固定を行うことに等しいといえます。

こちらも簡単な例として、線形合同法によるPRNGの生成式から確認してみましょう。

X_{n+1} = (aX_n+c) \mod{M}
初期値として X_0 を与えると、以降の全ての X_n は確定的になりますので、シードの固定は実質的に X_0 を固定するという操作になります。

 2.3. 乱数生成数とPRNGの内部状態の進行数の不一致ここからはややテクニカルな内容ですが、並列化に関係する知識として必要なものになります。

一様乱数以外の分布の乱数を生成させたとき、乱数の生成数とPRNGの内部状態の進行数が一致しないことがあります。PRNGをある(恣意的な)シードで固定した際に、以下の2つのケースの生成結果を見てみましょう。


パターン
[1]:最初の10個の分布
[2]: 次の10個の分布
[3]: 最後の10個の分布


A
一様分布
一様分布
一様分布

B
一様分布
標準正規分布
一様分布

import numpy as np

# パターンA
pcg_gen_A = np.random.Generator(np.random.PCG64(seed=13)) # 擬似乱数生成器の固定

unif_A_1 = pcg_gen_A.uniform(0,1,10)
unif_A_2 = pcg_gen_A.uniform(0,1,10)
unif_A_3 = pcg_gen_A.uniform(0,1,10)

# パターンB
pcg_gen_B = np.random.Generator(np.random.PCG64(seed=13)) # 擬似乱数生成器の固定

unif_B_1 = pcg_gen_B.uniform(0,1,10)
gauss_B_2 = pcg_gen_B.standard_normal(10)    
unif_B_3 = pcg_gen_B.uniform(0,1,10)
その結果をプロットしたものが以下になります。

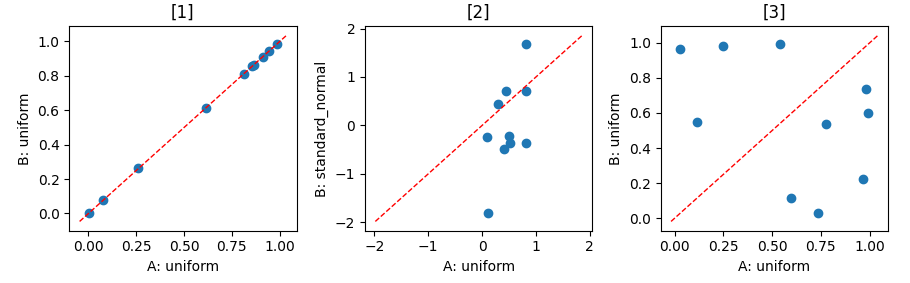
まず、それぞれPRNGは乱数生成前に固定をしているため、最初の10個は全く同じ乱数が生成されていることが確認できます（左図）。次の10個は異なる分布の乱数を生成しているため、異なる結果であることは当然です(中央図)。問題は最後の10個ですが、同じ一様乱数を発生させているにも関わらず、最後の一様乱数の結果が異なることが確認できます（右図）。
この現象は正規乱数の生成を行うことで発生していますが、他の分布でも発生することがあります。正規乱数については、numpyではZiggurat法による生成アルゴリズムが採用されています。これは棄却採択法の一種であり、あるstateから生成される乱数が正規乱数とならずに棄却されるケースが存在することから、結果的に1つの正規乱数を得るために複数のstateを消費する可能性があります。


正規乱数を発生させる際に棄却されたケースの状況イメージ
その他細かな補足については以下にまとめますので、適宜ご参照ください。
本節の補足
Ziggurat法についての詳細はこちらの説明に委ねます。Pythonではないですが、棄却採択法の概念やロジックの整理が分かりやすいと思います。なお、棄却率は約1%程度とされています。
https://andantesoft.hatenablog.com/entry/2023/04/30/183032
また、numpyのPCG64に関するドキュメントにも本現象に関する注意事項が記されています。特に1つ目に相当します。
https://numpy.org/doc/stable/reference/random/bit_generators/generated/numpy.random.PCG64.advance.html
なお、一様乱数の生成は、PRNGの内部状態のstateを用いた決定的な変換が用いているため、乱数生成数とPRNGの内部状態の進行数は比例します。詳細は割愛しますが、以下に簡単な補足を掲載します。
ベースロジックの元はこちらになるかと思われます。(numpyでも使用とされている)。numpyのライブラリでもfloatケースについては同様のロジックを確認していますが、64bitのケースの全てを追い切れていないため、この点はご了承ください。
https://github.com/tc39/proposal-seeded-random?tab=readme-ov-file
なお、上記のロジックからお試しで以下のようなコードを実行すると、同じ一様乱数が得られることが確認できます。このことから、PCG64に関しては、1つのstateに対して1つの一様乱数が対応づいています。
    pcg_gen = np.random.Generator(np.random.PCG64(seed=42))

    # 実際にロジックに従って一様乱数を生成させた例
    x = pcg_gen.bit_generator.random_raw()
    unif_1 = (x >> 11) * (1.0 / (1 << 53))

    pcg_gen = np.random.Generator(np.random.PCG64(seed=42)) # 再初期化

  # 通常通り、一様乱数を生成させた例
    unif_2 = pcg_gen.uniform(0,1,1)[0]
  
    print(f" unif_1: {unif_1},\n unif_2: {unif_2}")
    """
     unif_1: 0.7739560485559633,
     unif_2: 0.7739560485559633
    """
  


 2.4. 同一シード上での並列化シミュレーションのイメージシードの異なる並列化を行う際は容易で、並列処理で与えるコアごとに異なるシードで固定したPRNGを与えればよいということになります。しかし、どの並列処理のコアでも同じシードで固定されたPRNGを使う際には「コアごとに進行度の異なるPRNGを与える」必要が出てきます。まずはこのアイデアについて考えていきます。



並列処理イメージ図
以下の表に3つの方法をまとめました。今回の想定ケースに対してどの方法が良いかを検討した結果、ロジックの解釈性の良さと効率性の観点を含めて条件に最も適合するものは節2.4.3の手法と考えます。
ただし、この手法を用いる際には追加で注意点が発生するため、次節2.5でさらに詳細を説明します。


section
方法
メリット
デメリット


2.4.1
目的地点まで乱数を生成してPRNGの内部状態を進める
ロジックが単純
・生成数の把握が必要　
・生成数が増えると厳しい

2.4.2
同一シードでも親シードと独立なPRNGの内部状態を生成
・生成数、バッファ考慮が不要
・ロジックが複雑

2.4.3
PRNGの内部状態をスキップする
ロジックが単純
・生成数の把握が必要  
 ・バッファの考慮  
・実装があるかはPRNG次第


 2.4.1 目的地点まで乱数を生成してPRNGの内部状態を進めるPRNGをシードで初期化後、既に生成し終わった分の乱数を再生成してPRNGの内部状態を進める方法です。並列処理イメージ図のグレー部分を生成して捨てる処理を行うことで、事実上意図するstateから生成を行うことができるというものです。シンプルですが、生成数が増えるほど時間とメモリ消費量が大きくなるため、できる限りこちらは採用したくないところです。

 2.4.2 同一シードでも親シードと独立なPRNGの内部状態を生成する方法同一シード下でも異なるPNRGを生成する方法として、numpyは並列処理時はこの方法を推奨しています。ロジックの詳細はこちらをご覧ください。利点としては、並列数が増えても親シードを変更しなくて良いという点にあり、容易に異なるPRNGを生成でき、かつ節2.4.2のようなバッファや乱数の生成数に対する考慮も不要となります。
技術的には便利な方法になりますが、今回の同一シード下での実験設定にはやや一致していないと考えています。実質的な操作としては「別シードを各並列時のコアごとに付与する」こととほぼ同じような操作で、並列処理での乱数生成における操作・管理を安全に行いやすい方法であると解釈しています。
そのため、今回の想定ケースでは採用に至りませんでしたが、乱数に対する厳密な管理が不要（厳密な再現性が求められない、シード自体が重要というわけではない、など）であれば、本節の方法を使うことが推奨されるという点に違和感はないと思います。

 2.4.3 PRNGの内部状態をスキップする方法PRNGをシードで初期化後、既に生成し終わった分だけPRNGの内部状態を進める方法で、並列処理イメージ図のグレー部分を予め指定してスキップしてしまうというものです。
シミュレーション前に乱数の生成数に検討がついている場合や把握が可能なケースで特に有効的で、かつ他者から見ても理解しやすいロジックですが、実際にこれが可能で効率的に行えるかどうかはPRNGのアルゴリズムに依存します。今回のPCG64は実は任意の数だけstateを進めるadvanceメソッドがあるため、こちらが現実的な選択肢になりました。
ただし、棄却採択法が用いられている分布に対してこの方法を用いる場合はPRNGの内部状態を予定している乱数生成数よりも多くスキップする必要があります。この点の詳細を次節に解説します。

 2.5 節2.4.3の手法に対する追加の注意点今回の想定ケースに対して、並列処理における再現性担保を行うためには節2.4.3の方法を採用します。しかしこの手法を用いる場合は、節2.3(乱数生成数とPRNGの内部状態の進行数の不一致)への対処が必須となります。
すなわち、バッファの確保（実際に生成させる乱数の数よりも多くPRNGの内部状態を進める）ということですが、十分に注意しないと結果が再現しないことになります。以下代表的な3つのケースについて解説します。なお、一様乱数のみ使用する場合は本節で挙がっている問題は当てはまらないことになります。
【問題ケース1】バッファ考慮を甘く見積もった結果、別コアで重複した乱数を発生させてしまう。余裕をもったバッファを確保することが推奨されます。



※分かりやすく、バッファを持たせないケースで考えると、赤塗部分の重複が問題箇所。


【問題ケース2】バッファを実際の生成で進行するstateよりも過剰に確保した場合、同一シード下でシミュレーションを1コアの直列処理を行った場合とNコアに並列処理した場合での結果が一致しない。直列で実行した場合に使われるはずのstateが使われないため、直列と並列が一致することはありません。これを一致させたい場合は、直列シミュレーションで実際に消費したstate数とその時に生成された実際の乱数の対応表を作成するしかありませんが、そもそも直列シミュレーションが難しいケースを想定しているため、そのような状況を作ることはあまり現実的ではありません。



※直列、並列では使用するstateに差が生じるので、2つの処理間では一般に結果は一致しない。


【問題ケース3】並列処理の各コアで実行するシミュレーション回数が可変のケースで、過去のシミュレーション結果が再現しない。ある実験時点ではシミュレーション総数に対して並列コア数を2で指定し行い、その後メモリの都合がよくなり3並列が可能になった場合に、並列コア数を3に変更して実験を行ってしまうと、一般に過去の結果と一致しません。
並列コア数を増やすほど、バッファの確保により連続的に使われないstateの列が増加します。このため、並列コア数を変更すると過去の実験ではバッファ領域であったstateを用いて乱数を生成してしまうためです。そのため、再現性を担保する上では、１コア当たりのシミュレーション回数を固定しておくことが重要です。


※合計3000個の正規乱数を作るとして、2コアは1500個ずつ、3コア並列は1000個ずつ生成したときの例
以上のことから、同一シード上で十分な再現性を得るには、単純な環境再現性のみならず以下の要素に注意することになります。
**ある程度余裕を持ったバッファ確保を行う
特に乱数を発生させる分布のアルゴリズムには注意する。

直列で計算した結果と並列計算した結果を混同しない
再現実験を行う際は、過去に計算した並列処理において、各コア単位に対するシミュレーション回数を変更しない
計算環境が可変のインスタンス下で計算する際には、結果を混同しないよう特に注意する


 3. 具体的な実装方法前章で述べた概念をもとに、それぞれどのように実装するかについて述べていきます。

 3.1 乱数の固定化と生成方法まず、使用するPRNGを指定し、シードの指定から乱数の固定化を行います。
import numpy as np

bg = np.random.PCG64(seed=42) # seedの指定は整数値で普段通り設定
rg = np.random.Generator(bg)

!なお、現在のnumpyバージョンでは、上記の記述はrg = np.random.default_rng(seed=42)として呼び出すことでも同じものが得られます。ただし、これは現在のデフォルトがPCG64に設定されているためであり、今後のバージョンでは変更される可能性がある点には注意します。
bgでは、BitGeneratorを定義しています。これまでのPRNGに相当するもので、真のstateであったり、stateの生値（ただし全て64bit出力）を見ることができます。設定可能なBitgeneratorの一覧は以下より確認できます。
https://numpy.org/doc/stable/reference/random/bit_generators/index.html
次に最も代表的な2つの乱数である、一様乱数と標準正規乱数を発生させるためのコードを確認します。
# 一様分布
unif_test = rg.uniform(0,1,size=1)

# 標準正規乱数
std_norm_test = rg.standard_normal(size=1)
上記の2つを用いて、乱数の再現性の基本となる部分を確認しておきます。
import numpy as np

# １．擬似乱数生成器を seed=42 で固定
rg = np.random.Generator(np.random.PCG64(seed=42))
unif_rvs_1 = rg.uniform(0,1,size=2)

print(f"[1] : unif_rvs = {unif_rvs_1}")

# ２．擬似乱数生成器を 別の seed=84 で固定
rg = np.random.Generator(np.random.PCG64(seed=84))
unif_rvs_2 = rg.uniform(0,1,size=2)

print(f"[2] : unif_rvs = {unif_rvs_2}")

# ３．擬似乱数生成器を seed=42 で固定して再び生成（-> 1と同じ結果が再現）
rg = np.random.Generator(np.random.PCG64(seed=42))
save_state = rg.bit_generator.state # [4]のために生成前に記録
unif_rvs_3 = rg.uniform(0,1,size=2)

print(f"[3] : unif_rvs = {unif_rvs_3}")

# ４．seed42の擬似乱数生成器のstateを復元して生成（-> 1と同じ結果が再現）
bg = np.random.PCG64() # seedの指定なし
bg.state = save_state  # stateの復元
rg = np.random.Generator(bg)
unif_rvs_4 = rg.uniform(0,1,size=2)

print(f"[4] : unif_rvs = {unif_rvs_4}")
こちらを実行した結果は次のようになります。
[1] : unif_rvs = [0.77395605 0.43887844]
[2] : unif_rvs = [0.73209824 0.90020366]
[3] : unif_rvs = [0.77395605 0.43887844]
[4] : unif_rvs = [0.77395605 0.43887844]
異なるseedで乱数を生成するケース([1]-[2])の生成結果は異なります。
同一シードで初期化を行った後に生成するケース([1]-[3])は結果が再現します。
[4]のケースは特殊ですが、特定のシードで初期化したPRNGの初期のstateを保持しておき、それを復元して生成を行ったものです。
これは[1]や[3]と同じstateを使用して乱数を生成することになるため、同じ生成結果が得られるということになります。


 3.2 Generatorのスキップ処理PCG64では、内部状態のstateを任意の数だけスキップさせることが可能で、advanceメソッドを用います。シード込で初期化したBitGeneratorに対してadvanceメソッドで指定のstate分を進めてからGeneratorでラップします。
また、併せてスキップなしのGeneratorとスキップありのGeneratorの2つで一様乱数を発生させるケースを試してみます。このとき、スキップなしのGeneratorは5つ一様乱数を発生させると、スキップありのstateになるため、その後の生成結果は同じになります。
# skipなしのGeneratorの定義
rg_base = np.random.Generator(np.random.PCG64(seed=42))

# stateを5つスキップしたGeneratorの定義
bg_skip5 = np.random.PCG64(seed=42)
bg_skip5.advance(delta=5)    # 指定の数だけstateをスキップ
rg_skip5 = np.random.Generator(bg_skip5)

# それぞれ一様分布を生成
## skipなしのgeneratorは6番目からはskipありのGeneratorに一致
print(f" rg_base: {rg_base.uniform(0,1,10)[5:]},\n rg_skip: {rg_skip5.uniform(0,1,5)}")
"""
 rg_base: [0.97562235 0.7611397  0.78606431 0.12811363 0.45038594],
 rg_skip: [0.97562235 0.7611397  0.78606431 0.12811363 0.45038594]
"""

 3.3 並列処理のための実装並列処理にはjoblibを用いますが、この部分で特別なことは特にありません。joblibの外側でパラメータを整理し、必要なGeneratorを準備しておくことが重要です。事前に考慮しておくべきパラメータをまとめると以下の表になります。


変数名
内容


TOTAL_SIMUL_SIZE
同一シード下でのシミュレーション総数

SIMUL_SIZE
各コアの1回あたりのシミュレーション回数(シナリオ数)

N_WORKERS
1回の並列で使用するコア数

N_GEN_RVS
1回のシミュレーションで発生させる乱数の数

N_PER_WORKER
1つのコアで消費するstate数 (バッファ込)

SIMUL_SEED
シミュレーションする乱数シード

イメージを付けるため、例として与信ポートフォリオにおける損失額分布の作成にモンテカルロシミュレーションを用いるケースを非常に簡略化して見てみます。なお、次章では実際に並列処理による乱数の再現性を確認を行いますが、このシミュレーションを行うわけではないため、あくまで設定としてどのような変数があれば良いかの理解の補足として取り上げます。
!与信先が貸し倒れる（=デフォルトする）と、与信元には貸した額が返ってこなくなるため、損失が発生します。このデフォルト状況を数理モデルを背後におきつつ乱数を生成することで、ある乱数値（シナリオ）の元での損失額が計算されます。これを繰り返すことで、損失額分布を計算することができ、VaRや非期待損失といった信用リスク量を計算します。
これらを取り入れて、必要なGeneratorを準備しておきます。
import numpy as np

# 節3.2の関数化
def make_rng(worker_id, seed, skip):
    bg = np.random.PCG64(seed)
    bg.advance(worker_id * skip)
    return np.random.Generator(bg)
    
# テーブルにまとめた変数
TOTAL_SIMUL_SIZE = 100000 
SIMUL_SIZE    = 10000     
N_WORKERS     = 5   
N_GEN_RVS     = 100 
N_PER_WORKER  = SIMUL_SIZE * N_GEN_RVS * 2 # バッファは乱数生成数の2倍で設定
SIMUL_SEED = 42

# その他補助変数 //////////////////////////////////
## 単一コアの乱数生成数
core_gen_rvs = SIMUL_SIZE * N_GEN_RVS

## 同一seed内での並列処理を呼び出す回数 (現設定では 2 )
same_seed_parallel_iter = TOTAL_SIMUL_SIZE // SIMUL_SIZE // N_WORKERS

## 同一seed内での単一シミュレーション回数の呼び出し総回数 (現設定では 10 )
same_seed_total_iter = N_WORKERS*same_seed_parallel_iter 

## 各シミュレーションごとの連番番号の付与（次章で使用）
range_index_list = [range(core_gen_rvs*i,core_gen_rvs*(i+1),1) for i in range(same_seed_total_iter)]
# ////////////////////////////////////////////////

# 各並列コアに与えるスキップ済Generatorを作成
rngs = [make_rng(k, SIMUL_SEED, N_PER_WORKER) for k in range(same_seed_total_iter)]


 4. 再現性における簡易検証とその結果実際に並列計算において、実験再現性が担保できるかという点や、節2.5で述べたようなケースが発生することを確認します。ここでの再現性検証として、シミュレーション部分は単純に正規乱数を発生させるということに留めます。それらを集約した際に各乱数が再現していれば、実際のシミュレーション結果も再現するということが保証されます。

 4.1 ベースコード以下のコードを用いて検証を行います。前節3.3に加えて以下のコードを追加して検証します。
コードを展開import numpy as np
import pandas as pd
from joblib import Parallel, delayed

# シミュレーションする関数（今回は乱数を生成するのみ）
def exec_simulation(rg, range_list, size_simulation):
    simul_core = rg.standard_normal(size_simulation)
    col_name = [f"x_{i}" for i in range_list]
    df = pd.DataFrame(np.array([simul_core]).T, index=col_name, columns=["result"])
    return df

# 並列処理の実行（exec_simulation関数を並列化）
def run_parallel(rngs, range_list, simul_size, n_jobs):
    results = Parallel(n_jobs=n_jobs)(
        delayed(exec_simulation)(
            rngs[i],                    # 各コアに対応する Generator を割り当てる
            range_list=range_list[i],   # 各コアでの乱数のナンバリングリスト
            size_simulation=simul_size, 
        )
        for i in range(n_jobs) 
    )

    # 各実行結果(df)を結合
    df_final = pd.concat(results)

    return df_final

# メイン処理
df_result_total = pd.DataFrame()

for iter_ in range(same_seed_parallel_iter):
    now_rngs = rngs[iter_*N_WORKERS: (iter_+1)*N_WORKERS] 
    now_range_index = range_index_list[iter_*N_WORKERS: (iter_+1)*N_WORKERS]
    
    # 各シミュレーションを実行
    df_result_iter = run_parallel(rngs=now_rngs, range_list=now_range_index, simul_size=core_gen_rvs, n_jobs=N_WORKERS)

    # 結果の積みあげ
    df_result_total = pd.concat([df_result_total, df_result_iter])

例えば、これを1000万回シミュレーションを行ったと仮定したとき、以下のようなデータフレームが出力されます。



result


x_0
0.304717

x_1
-1.039984

x_2
0.750451

...
...

x_9999997
-0.644783

x_9999998
-1.284355

x_9999999
-0.717833


 4.2 検証パターンまずは、各検証パターンの設定として共通部分を以下のように設定します。このもとで、並列条件などを変更したときの結果を比較します。
1回のシミュレーションでは、100個の正規乱数を使用すると仮定
N_GEN_RVS = 100

このシミュレーションを合計10万回繰り返す（正規乱数は合計1000万個生成）
TOTAL_SIMUL_SIZE = 100000

次に、各検証パターンの設定です。生成する乱数は、正規乱数のケースと一様乱数のケースそれぞれを確認します。
正規乱数の場合：
[1]-[2] ：直列と並列の結果が一致しないことの確認
[2]-[3,4]：コア毎の生成数が同じかどうかで結果の再現性が変わることを確認
[2]-[4]は一致しない設定になりますが、[2]-[3]は事前に渡すGeneratorを正しく実装できていれば同じ結果になると想定しています。

[2]-[5]：バッファを取らないと結果が変わることの確認
[1]-[5]：並列処理でバッファを取らない場合でも直列と一致しないことも確認





検証パターン
SIMUL_SIZE
N_WORKERS
コア毎乱数生成数
バッファ


1
直列
100000
1
10000000
-

2
並列(5コア_固定)
10000
5
1000000
2000000

3
並列(10コア_固定)
10000
10
1000000
2000000

4
並列(5コア_総数割)
20000
5
2000000
4000000

5
並列(10コア_固定_バッファ無)
10000
10
1000000
1000000


 4.3 検証結果
 4.3.1 結果の概要まずは、各1000万個の生成結果を並べたものになります。なお、値の見やすさのため、小数第4位以降をカットしています。
最初の時点ではどのパターンの生成結果も一致しており、スタートの条件が揃っていることが確認できますが、最終盤の生成結果は異なる値となっています。この現象はどれも2章で話した内容で説明されます。


idx
[1]:直列
[2]:並列
(10コア固定)
[3]:並列
(5コア固定)
[4]:並列
(5コア総数割)
[5]:並列
(10コア固定_バッファ無)


x_0
0.304
0.304
0.304
0.304
0.304

x_1
-1.039
-1.039
-1.039
-1.039
-1.039

x_2
0.750
0.750
0.750
0.750
0.750

x_3
0.940
0.940
0.940
0.940
0.940

x_4
-1.951
-1.951
-1.951
-1.951
-1.951

...
...
...
...
...
...

x_9999995
0.258
-0.935
-0.935
-0.130
1.109

x_9999996
2.124
0.385
0.385
0.553
0.452

x_9999997
0.093
-0.644
-0.644
0.941
1.118

x_9999998
-0.970
-1.284
-1.284
1.251
1.074

x_9999999
0.580
-0.717
-0.717
1.094
-0.613

また、各処理に対する乱数の一致率を算出したものがこちらになります。一致率ごとの状況を整理します。
一致率 0.1 ：最初の100万個のみ一致する。
一致率 0.2 ：最初の200万個のみ一致する。
一致率 0.5 ：今回の設定において規則的なかみ合いが発生しており、全体の半分が一致する。
一致率 1   ：すべての生成結果が一致する。[2]-[3]は同じ生成が行われていることになる。



[1]:直列
[2]:並列
(10コア固定)
[3]:並列
(5コア固定)
[4]:並列
(5コア総数割)
[5]:並列
(10コア固定_バッファ無)


[1]
1
0.1
0.1
0.2
0.1

[2]

1
1
0.5
0.1

[3]


1
0.5
0.1

[4]



1
0.1

[5]




1


 4.3.2 生成結果が一致しないパターンの詳細確認について基本的な不一致の要因は2章で話しているものの、直列と並列（バッファ無）の[1]-[5]について少しだけ掘り下げて確認してみます。コアが切り替わる部分で差が生じることは分かっているため、乱数生成が95万～105万個の間に着目してみます。
並列処理で生成されている乱数の生成結果が、直列の乱数ではどの位置で生成されたものかを検出し、その位置をプロットすることで確認できます。
プロットした結果、100万個から先の時点で縦軸の値が対角線よりも下に来ていることが分かり、並列処理では、棄却された正規乱数の分だけ重複が発生していることが確認できます。また、本シードにおける正規乱数の棄却率も約2%よりも少し多いということも見て取れます。
このことから、バッファに必要性を再確認するとともに、生成したい分布に対して今のライブラリにおいて棄却採択率がどの程度であるかを実証的に確認しておくことも有効といえます。

 5. 補足事項について
 5.1 計算結果のcsv保存と再現性について再現性の観点では、シミュレーションした結果を保存しておくということも考えられます。その際の保存形式にcsvを選択する場合、再計算した際の値と完全には一致しないことがあるため、型の取り扱いという点においてはこちらも注意が必要といえます。
import numpy as np, pandas as pd

# 正規乱数を1000万個生成
rng_g = np.random.Generator(np.random.PCG64(42))
arr = rng_g.standard_normal(10_000_000)
df_raw = pd.DataFrame({"x": arr})

# 各種それぞれの形式で保存
df_raw.to_parquet("x.parquet", engine="pyarrow", compression="zstd")
df_raw.to_csv("x.csv")

# 再び呼び出してデータを結合
df_parquet = pd.read_parquet("x.parquet").rename(columns={"x":"parquet"})
df_csv = pd.read_csv("x.csv", index_col=0).rename(columns={"x":"csv"})
df = pd.concat([pd.concat([df_raw, df_parquet],axis=1), df_csv],axis=1)

# ///////////////////////////////////////

# 一致するかを確認
print(f' raw - par : {np.array_equal(df["x"].values, df["parquet"].values)}')
print(f' raw - csv : {np.array_equal(df["x"].values, df["csv"].values)}')
print(f' csv - par : {np.array_equal(df["csv"].values, df["parquet"].values)}')

# 結果 -> csv保存をすると一致しない：
 raw - par : True
 raw - csv : False
 csv - par : False

# 1つの値で一致するかを確認
print(f'idx=0:\n raw: {df["x"][0]}, \n par: {df["parquet"][0]}, \n csv: {df["csv"][0]}')
print(f'idx=1:\n raw: {df["x"][1]}, \n par: {df["parquet"][1]}, \n csv: {df["csv"][1]}')

# 結果
idx=0:
 raw: 0.30471707975443135, 
 par: 0.30471707975443135, 
 csv: 0.3047170797544313
idx=1:
 raw: -1.0399841062404955, 
 par: -1.0399841062404955, 
 csv: -1.0399841062404955


 5.2. scipyライブラリでの乱数生成の固定方法乱数を生成するという点においては、scipyライブラリを使用することもあるかと思います。

同じように標準正規乱数を生成したい場合、一般に次のようなコードを記述します。
scipy.stats.norm.rvs(size=10, random_state=None)
この時、random_stateには通常int型のシード値を入力して使用することが多いかと思われますが、ここにnumpy.random.Generatorを定義し、引数として与えることができます。そのため、分布生成アルゴリズムが同一である場合は、以下の乱数生成は同じ結果が得られることになります。
標準正規分布の乱数をnumpy, scipyで発生させて、一致するかの簡易検証を行った結果を記します。

なお、参考値ではありますが、5億個を生成した時間は numpy: 5.11s, scipy: 5.92sとなり、numpyの方が早いようでした。
seed=42
gen = np.random.Generator(np.random.PCG64(seed))
scipy_rvs = scipy.stats.norm.rvs(size=500_000_000, random_state=gen)

gen = np.random.Generator(np.random.PCG64(seed))
numpy_rvs = gen.standard_normal(size=500_000_000)

print(np.array_equal(scipy_rvs , numpy_rvs)) # -> True
scipyのrandom_stateに関する挙動の詳細はこちらを参照ください。

https://docs.scipy.org/doc/scipy-1.15.3/reference/generated/scipy.stats.rv_continuous.rvs.html

 6. まとめ同一シード上での乱数生成数の規模が大きいモンテカルロ・シミュレーションについて、特に並列処理を行う上での実験再現性の担保の検討を行ってきました。

今回の想定ケースにおいては、解釈性・効率性の観点からGeneratorの内部状態をスキップする方法が最良としつつも、内部仕様にも少し踏み込み、技術的な注意点についても解説しました。
近年はPythonを用いたコーディングが増えていると思いますので、モンテカルロ・シミュレーションも自然に使っている機会もあるかと思います。実務的な制約の中での検討という点もあり、一般の業務として今回の想定ケースが完全に当てはまるということは少ないかもしれませんが、本記事が何かの機会に参考になれば幸いです。

パターン	[1]:最初の10個の分布	[2]: 次の10個の分布	[3]: 最後の10個の分布
A	一様分布	一様分布	一様分布
B	一様分布	標準正規分布	一様分布

section	方法	メリット	デメリット
2.4.1	目的地点まで乱数を生成してPRNGの内部状態を進める	ロジックが単純	・生成数の把握が必要　・生成数が増えると厳しい
2.4.2	同一シードでも親シードと独立なPRNGの内部状態を生成	・生成数、バッファ考慮が不要	・ロジックが複雑
2.4.3	PRNGの内部状態をスキップする	ロジックが単純	・生成数の把握が必要・バッファの考慮・実装があるかはPRNG次第

変数名	内容
TOTAL_SIMUL_SIZE	同一シード下でのシミュレーション総数
SIMUL_SIZE	各コアの1回あたりのシミュレーション回数(シナリオ数)
N_WORKERS	1回の並列で使用するコア数
N_GEN_RVS	1回のシミュレーションで発生させる乱数の数
N_PER_WORKER	1つのコアで消費するstate数 (バッファ込)
SIMUL_SEED	シミュレーションする乱数シード

	result
x_0	0.304717
x_1	-1.039984
x_2	0.750451
...	...
x_9999997	-0.644783
x_9999998	-1.284355
x_9999999	-0.717833

	検証パターン	SIMUL_SIZE	N_WORKERS	コア毎乱数生成数	バッファ
1	直列	100000	1	10000000	-
2	並列(5コア_固定)	10000	5	1000000	2000000
3	並列(10コア_固定)	10000	10	1000000	2000000
4	並列(5コア_総数割)	20000	5	2000000	4000000
5	並列(10コア_固定_バッファ無)	10000	10	1000000	1000000

idx	[1]:直列	[2]:並列 (10コア固定)	[3]:並列 (5コア固定)	[4]:並列 (5コア総数割)	[5]:並列 (10コア固定_バッファ無)
x_0	0.304	0.304	0.304	0.304	0.304
x_1	-1.039	-1.039	-1.039	-1.039	-1.039
x_2	0.750	0.750	0.750	0.750	0.750
x_3	0.940	0.940	0.940	0.940	0.940
x_4	-1.951	-1.951	-1.951	-1.951	-1.951
...	...	...	...	...	...
x_9999995	0.258	-0.935	-0.935	-0.130	1.109
x_9999996	2.124	0.385	0.385	0.553	0.452
x_9999997	0.093	-0.644	-0.644	0.941	1.118
x_9999998	-0.970	-1.284	-1.284	1.251	1.074
x_9999999	0.580	-0.717	-0.717	1.094	-0.613

	[1]:直列	[2]:並列 (10コア固定)	[3]:並列 (5コア固定)	[4]:並列 (5コア総数割)	[5]:並列 (10コア固定_バッファ無)
[1]	1	0.1	0.1	0.2	0.1
[2]		1	1	0.5	0.1
[3]			1	0.5	0.1
[4]				1	0.1
[5]					1

MTEC Tech BlogPublication

三菱UFJトラスト投資工学研究所 (MTEC) のTech Blogです。各記事の内容は個人の見解であり、所属する組織の公式見解ではありません。

1. はじめに

1.1 各種設定

1.2 キーポイントの整理

【2章】再現性担保のために必要な概念について

【3・4章】具体的な実装方法と簡易検証

【5章】補足情報

2. 再現性担保のために必要な概念について

2.1. ある分布の乱数を生成するイメージの理解

2.2. 乱数の生成結果の固定

2.3. 乱数生成数とPRNGの内部状態の進行数の不一致

2.4. 同一シード上での並列化シミュレーションのイメージ

2.4.1 目的地点まで乱数を生成してPRNGの内部状態を進める

2.4.2 同一シードでも親シードと独立なPRNGの内部状態を生成する方法

2.4.3 PRNGの内部状態をスキップする方法

2.5 節2.4.3の手法に対する追加の注意点

【問題ケース1】バッファ考慮を甘く見積もった結果、別コアで重複した乱数を発生させてしまう。

【問題ケース2】バッファを実際の生成で進行するstateよりも過剰に確保した場合、同一シード下でシミュレーションを1コアの直列処理を行った場合とNコアに並列処理した場合での結果が一致しない。

【問題ケース3】並列処理の各コアで実行するシミュレーション回数が可変のケースで、過去のシミュレーション結果が再現しない。

3. 具体的な実装方法

3.1 乱数の固定化と生成方法

3.2 Generatorのスキップ処理

3.3 並列処理のための実装

4. 再現性における簡易検証とその結果

4.1 ベースコード

4.2 検証パターン

4.3 検証結果

4.3.1 結果の概要

4.3.2 生成結果が一致しないパターンの詳細確認について

5. 補足事項について

5.1 計算結果のcsv保存と再現性について

5.2. scipyライブラリでの乱数生成の固定方法

6. まとめ

Discussion