(Bell-)CHSH不等式を導出し、量子論ではそれが破れることを見ます。さらに、IBMの量子コンピュータを使って破れを実験的に観察します。
リハビリです。
CHSH不等式
(Bell-)Clauser-Horne-Shimony-Holt不等式((Bell-)CHSH不等式)は、ふたつの粒子のスピンに関するある種の相関について成り立つ不等式です。この不等式は局所実在論を仮定する限り成立します。導出の前に、局所実在論とは何かを見ましょう。
局所実在論
物理学的な意味での局所実在論は、以下の仮定を満たす理論の総称です:
-
局所性: 超光速通信ができない。
-
実在性: すべての物理量は、観測されるか否かに限らず、すべての時刻で確定した値を取る。
かなり当たり前ではないでしょうか?局所性は相対論的観点から当然のように思われます。もし超光速通信が可能であれば、過去との通信が可能となり、因果律が破綻します。実在性も経験的に当たり前に成り立つように思われます。夜の間は太陽の位置が確定していないなどという事はありえないはずです。
古典力学や電磁気学、熱力学のような局所性と実在性を仮定した物理理論においては、CHSH不等式が常に成立します。以下でこれを導出します。
スピンの測定によるCHSH不等式の導出
思考実験の設定
スピン1/2の粒子1と粒子2が、一つの粒子が崩壊することで発生したとします。二人の観測者AとBがそれぞれ粒子1と粒子2を次のように測定するとします。AとBには双方とも x 軸正の方向から粒子が入射されるとし、またそれぞれ y-z 平面で z 軸から \Theta と \Phi だけずれた方向を上向きとして測定するとします。
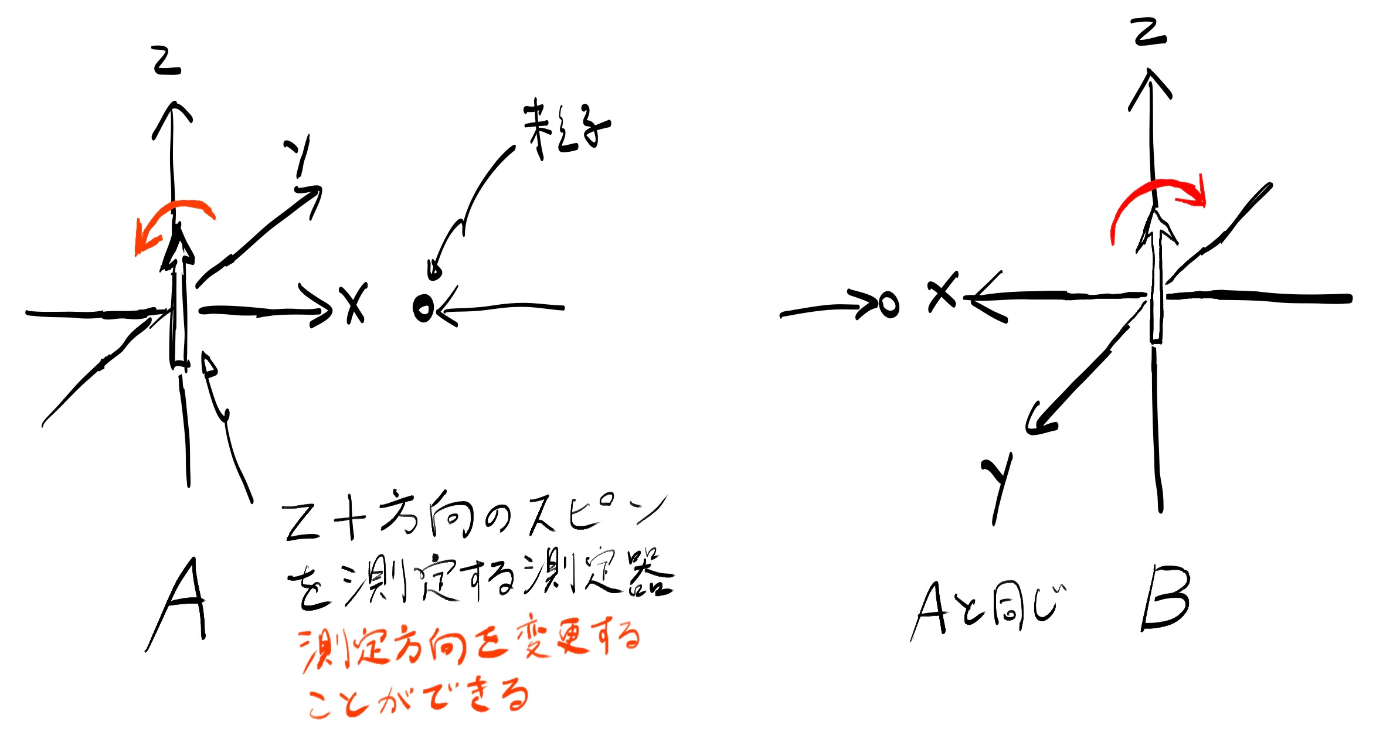
\Theta も \Phi もそれぞれの観測者が粒子を観測するまで自由に変更できるとします。さらに、スピン上向きを観測した場合には観測値を +1, 下向きを観測した場合は -1 としておきます。たとえば、もし \Theta = \Phi = 0 だとすると、A, Bともに z 軸方向のスピンを測定することになります。この際、Aが +1 (z 軸方向スピン上向き)を観測したとすると、角運動量保存則から、Bは -1 を観測する事になります。
さて、局所実在論では、実在性から二つのスピンの向きは観測される前から決定されています。ただし、各観測者には制御不可能な変数(崩壊後に送られてくる途中でスピンが外部の系と相互作用したりする)によって、スピンの上下は確率的に揺らぎます。この変数を \Lambda と書きましょう。\Lambda は、Bが観測する直前までに各粒子のスピンに影響を与えます。\Lambda が確定値 \lambda を取る確率を \mathrm{Pr}[\Lambda = \lambda] とします(\Lambda = \lambda であることは神のみが知りえますが、実在性から決定はしています)。このとき、測定方向が \Theta であるAが a \in \{+1, -1\} のスピンを測定する事象は、Aが A を観測するスピンの方向 \Theta を変数として、 A(\Theta) = a(\Theta, \lambda) と書けるでしょう。そして同様に、測定方向 \phi であるBが b \in \{+1, -1\} のスピンを測定する事象は、B をBが観測するスピンの方向を変数として、 B(\Phi) = b(\Phi, \lambda) と書けるでしょう。ここで、A(\Theta), B(\Phi) という表記に局所性が仮定されていることに注意してください。どこに仮定されているかというと、A はBの測定方向 \Phi に、B はAの測定方向 \Theta に依存しないという点です。これは、他方の観測者がどのような方向で測定していたとしても、自分の測定には影響しないのだ、という事を反映しています(正確には、相対論的な範囲で互いの観測角度が影響しあわないように測定を実行できるし、またそのように測定を実行すると仮定しています)。
以上の状況で、AとBがそれぞれ粒子のスピンを測定し終わるまでをひとつの測定シークエンスとして、次のような実験を考えましょう:
- Aは、各測定シークエンスにおいて、自身の測定角度 \Theta を、あらかじめ設定していた二つの角度 \theta と \theta' のどちらか一方に自由に設定する。
- Bは、各測定シークエンスにおいて、自身の測定角度 \Phi を、あらかじめ設定していた二つの角度 \phi と \phi' のどちらか一方に自由に設定する。
- 測定シークエンスを十分な回数繰り返す。
CHSH不等式
ここで突然、相関物理量
S = A(\theta) B(\phi) + A(\theta') B(\phi) - A(\theta) B(\phi') + A(\theta') B(\phi')
の期待値の絶対値
\begin{align*}
|\langle S \rangle| = |\langle A(\theta) B(\phi) \rangle + \langle A(\theta') B(\phi) \rangle - \langle A(\theta) B(\phi') \rangle + \langle A(\theta') B(\phi') \rangle|
\end{align*}
を計算します。微妙に対称になっていないところがミソです。例えば \langle A(\theta) B(\phi) \rangle は、
\begin{align*}
\langle A(\theta)B(\phi) \rangle &= \sum_\lambda \mathrm{Pr}[\Lambda = \lambda] a(\theta, \lambda) b(\phi, \lambda)
\end{align*}
となります。以上では \Lambda は離散的な確率を取るとしましたが、連続でも特に変わりはありません。以下面倒なので a = a(\theta, \theta), a' = a(\theta', \lambda), b = b(\phi, \lambda), b' = b(\phi', \lambda) と書きましょう。
すると、|\langle S \rangle| について
\begin{align*}
|\langle S \rangle| &= \left|\sum_\lambda \mathrm{Pr}[\Lambda = \lambda] (ab + a'b - ab' + a'b')\right| \\
& \leq \sum_\lambda |\mathrm{Pr}[\Lambda=\lambda] (ab + a'b - ab' + a'b')| \\
& = \sum_\lambda \mathrm{Pr}[\Lambda=\lambda] |ab + a'b - ab' + a'b'| \\
\end{align*}
を得ます。|\langle S \rangle| について、
\begin{align*}
|ab + a'b - ab' + a'b'| &= |(a + a') b - (a - a') b'| \\
&\leq |a + a'| |b| + |a - a'| |b'| \\
&= |a + a'| + |a - a'|
\end{align*}
が成立しますが、a, a' \in \{\pm 1\} から、最後の値は 2 になります。よって、|\langle S \rangle| は上から評価できて、
\begin{align*}
|\langle S \rangle| \leq 2 \sum_\lambda \mathrm{Pr}[\Lambda = \lambda] = 2
\end{align*}
が成立します。これがCHSH不等式です。
CHSH不等式の最大値の達成
|S| = 2 は実際に成立させることができます。|\langle S \rangle| \leq 2 はスピン1/2の系を用いて導出しましたが、このような変数を無視できるような系でも成立します(導出は簡単)。有名な例は、地球と月の間に浮かぶ宇宙船において、たい焼きを頭の部分としっぽの部分に分割して片方を地球に、もう片方を月に完全にランダムに投げる実験です。地球にいるAは、たい焼きのどちらかの部分が来る前に、頭の方を食べたいと考えている場合は \Theta = 0、しっぽの方を食べたい場合は \Theta = \pi と決めておきます(ここでは 0 や \pi の値はもはや角度ではないし、その値が重要な訳でもありません。便宜上角度のように書いていますが、異なる値であればなんでもよいです)。そして、物理量 A の観測値を、食べたいと思っている部分 \Theta が飛んで来たら +1, そうでなければ -1 として測定を行います。
これは次の表にまとめられます;
| 頭かつ \Theta = 0
|
頭かつ \Theta = \pi
|
しっぽかつ \Theta = 0
|
しっぽかつ \Theta = \pi
|
| +1 |
-1 |
-1 |
+1 |
物理量 B についても同様に次の表のように決めて測定を行います
| 頭かつ \Phi = 0
|
頭かつ \Phi = \pi
|
しっぽかつ \Phi = 0
|
しっぽかつ \Phi = \pi
|
| +1 |
-1 |
-1 |
+1 |
ここで、S の定義において、\theta= 0, \theta' = \pi, \phi = 0, \phi' = \pi とすして A(\theta) B(\phi) について考えてみると、頭の方を食べたいというAとBの欲求は同時に満たされることはあり得ないため、この値は常に -1 となります。同様に計算していくと、A'B = 1, AB' = 1, A'B' = -1 となるので、|\langle S \rangle| = 2 となります。
CHSH不等式不等式の破れ
量子論では、CHSH不等式を破ることができます。これはつまり、量子論の世界(おそらく我々が住んでいる世界)では、局所性または実在性が成り立たないということになります。そんなことある?以下では量子論におけるCHSH不等式の破れを見ていきましょう。
量子論におけるスピンの測定 A(\theta) はどのようになるのでしょうか?スピンの測定 A(\theta) は Z 基底を x 軸まわりに \theta ぶんだけ回転した基底で測定を行うことに対応するでしょう。この測定は、R_x(\theta) = \exp (-i \theta X/2) = \cos \theta/2 - i \sin \theta/2 Xとして R_x(\theta) Z R_x(- \theta) の固有ベクトルによる測定で与えられます。よって、スピンの測定 A(\theta) を表す物理量(これも A(\theta) と書きましょう)は
A(\theta) = R_x(\theta) Z R_x(- \theta)
と書くことができるでしょう。
同様にスピンの測定 B(\phi) は R_x(\phi) Z R_x(- \phi) の固有ベクトルによる測定で与えられ、それを表す物理量は
B(\phi) = R_x(\phi) Z R_x(- \phi)
と書くことができます。
2つのスピンの合成状態 \Psi の下での物理量 A(\theta) \otimes B(\phi) の期待値 \langle A(\theta) \otimes B(\phi) \rangle_{\Psi} は
\begin{align*}
\langle A(\theta) \otimes B(\phi) \rangle_\Psi &= \langle \Psi, (A(\theta) \otimes B(\phi)) \Psi \rangle
\end{align*}
で表されますから、\Psi をBell状態と呼ばれる状態(のひとつ)である
|\Psi^-\rangle = \dfrac{1}{\sqrt2}(|00\rangle - |11\rangle)
とすると、頑張って計算を行うことで、
\begin{align*}
\langle A(\theta) \otimes B(\phi) \rangle_{\Psi^-} &= \langle \Psi^-, (A(\theta) \otimes B(\phi)) \Psi^- \rangle \\
&= \cos (\theta - \phi)
\end{align*}
となるので、状態 \Psi^- の下での量子版の相関 S の期待値は
\langle S \rangle_{\Psi^-} = \cos (\theta - \psi) + \cos (\theta' - \psi) - \cos (\theta - \psi') \cos (\theta' - \psi')
となります。\langle S \rangle_{\Psi^-} の最大値を計算すれば、
\begin{align*}
\theta - \phi &= \pi / 4, \\
\theta' - \phi &= - \pi / 4, \\
\theta - \phi' &= 3 \pi / 4, \\
\theta' - \phi' &= \pi / 4
\end{align*}
が満たされる時、たとえば
\begin{align*}
\theta &= 0, \\
\theta' &= - \pi / 2, \\
\phi &= - \pi / 4, \\
\phi' &= - 3 \pi / 4
\end{align*}
の時に、
\langle S \rangle_{\Psi^-} = 2 \sqrt2 > 2
となり、CHSH不等式が破れます。
実験!
最後にIBMの量子コンピュータであるIBM Quantumを使って実験で破れを観察します。局所性または実在性が破られるなんてことがあるのでしょうか?
IBM Quantumは、Qiskitと呼ばれるPythonモジュールを通して動かすことができます。無料です。
まず量子回路を組まなければなりませんが、IBM Quantum での測定は Z 基底測定(Z の固有ベクトルである |0\rangle, |1\rangle への射影測定)しか行うことが出来ません。どうしましょう。
Z 測定の期待値
ここで一般の二量子ビット系の状態 \Psi と物理量 Z \otimes Z を考えましょう。
すると期待値 \langle Z \otimes Z \rangle_{\Psi} は
\begin{align*}
\langle Z \otimes Z \rangle_\Psi &= \langle \Psi, (Z \otimes Z) \Psi \rangle \\
&= \langle \Psi, (|00\rangle \langle00| - |01\rangle \langle01| - |10\rangle \langle 10| + |11\rangle \langle11|) \Psi \rangle \\
&= |\langle00, \Psi\rangle|^2 + |\langle11, \Psi\rangle|^2 - |\langle01, \Psi\rangle|^2 - |\langle10, \Psi\rangle|^2 \\
&= \mathrm{Pr}[a=0, b=0 | \Psi] + \mathrm{Pr}[a=1, b=1 | \Psi] - \mathrm{Pr}[a=0, b=1 | \Psi] - \mathrm{Pr}[a=1, b=0 | \Psi]
\end{align*}
となり、Z 測定をたくさん行ってその頻度を足し引きすれば決まります。
CHSH不等式の期待値
都合の良いことに、CHSH相関の各項の期待値は
\begin{align*}
\langle A(\theta) \otimes B(\phi) \rangle_{\Psi^-} &= \langle \Psi^-, A(\theta) \otimes B(\phi) \Psi^- \rangle \\
&= \langle \Psi^-, (R_x(\theta) Z R_x(- \theta)) \otimes (R_x(\phi) Z R_x(- \phi)) \Psi^- \rangle \\
&= \langle (R_x(- \theta) \otimes R_x(- \phi)) \Psi^-, (Z \otimes Z)(R_x(- \theta) \otimes R_x(- \phi)) \Psi^- \rangle \\
&= \langle Z \otimes Z \rangle_{(R(-\theta) \otimes R(-\phi))\Psi^-}
\end{align*}
のように変形できます。つまり、\langle A(\theta) \otimes B(\phi) \rangle_{\Psi^-} は、まずAとBが、送られてきた粒子のスピンをそれぞれ - \theta, - \phi だけ回転させた状態
\Psi' = (R_x(- \theta) \otimes R_x(- \phi)) \Psi^-
を用意し、そしてそのもとでの物理量 Z \otimes Z を測定することに等しい事が分かります。

つまり、\langle A(\theta) \otimes B(\phi) \rangle_{\Psi^-} を得るためには、状態 \Psi' を用意し、そのもとで物理量 Z \otimes Z の測定を繰り返して測定値の出現確率を計算して足し引きすればよい事になります。これで、IBM Quantumでの実験を行うことができます。
量子回路の作成
Qiskitというか一般の量子回路では、初めに指定した数の量子ビットを、すべて Z の固有ベクトルで固有値 +1 である |0\rangle として用意します。そしてそれらの量子ビットに各種操作を行って望みの状態を作り出す訳です。
我々はBell状態 \Psi^- を用意し、それに対して Z \otimes Z 測定を行えばよい訳です。
状態 \Psi^- の用意
状態 \Psi^- は、Hadamardゲート
H = \dfrac{1}{\sqrt{2}} \left(
\begin{matrix}
1 & 1 \\
1 & -1
\end{matrix}
\right),
CNOTゲート
C_{NOT} = \left(
\begin{matrix}
1 & & & \\
& 1 & & \\
& & 0 & 1 \\
& & 1 & 0 \\
\end{matrix}
\right),
およびCZゲート
C_Z = \left(
\begin{matrix}
1 & & & \\
& 1 & & \\
& & 1 & \\
& & & -1 \\
\end{matrix}
\right)
を使って、
\Psi^- = C_Z C_{NOT} (H \otimes 1) |00\rangle
のように用意できます。これらは量子回路の基本的なゲートで、Qiskitでは、QuantumCircuit クラスのメソッド h, cx, cz としてそれぞれ実装されています。
ここまでの回路は、

のように書けます。
物理量 A(\theta) \otimes B(\phi) の状態 \Psi^- の下での測定
先に述べたように、物理量 A(\theta) \otimes B(\phi) の状態 \Psi^- の下での測定は、物理量 Z \otimes Z を状態 (R_x(- \theta) \otimes R_x(- \phi)) \Psi^- の下での測定に等しいのでした。よって、我々は、先の回路 \Psi^- = C_Z C_{NOT} (H \otimes 1) |00\rangle の各系にそれぞれ回転を加えます。この回転も QuantumCircuit クラスのメソッド rx として実装されています。
測定直前の状態 \Psi' は、
\begin{align*}
\Psi' &= (R_x(- \theta) \otimes R_x(- \phi)) \Psi^- \\
&= (R_x(- \theta) \otimes R_x(- \phi)) C_Z C_{NOT} (H \otimes 1) |00\rangle
\end{align*}
であるから、回路図は

となります。
そしてこれらを計算基底で測定することで、測定値 00, 01, 10, 11 の各値が確率的に得られます。測定は QuantumCircuit の measurement メソッドで実装されています。
回路は

となります。
実験
CHSH相関を量子論において最大化するのは(\theta, \theta', \phi, \phi') = (0, - \pi / 2, - \pi / 4, - 3 \pi / 4) でした。ここで、\theta を固定せずに
S(\theta) = A(\theta) \otimes B(-\pi/4) + A(-\pi/2) \otimes B(-\pi/4) - A(\theta) \otimes B(-3\pi/4) + A(-\pi/2) \otimes B(-3\pi/4)
として、\theta をいろいろに動かしてみましょう。
S(\theta) の状態 \Psi^- の下での期待値は、次の4つの回路




をそれぞれ大量に実行し、各測定値の出現確率を求めるとよいです。
\langle S(\theta) \rangle を理論、シミュレーション、IBMQにおける実験で確かめたのが次の図です。特にシミュレーションと実験では、\theta = 0, \pi/4, 2\pi/4, \ldots, 8\pi/4=2\pi で、S の各項で4000ショットずつの測定を行いました。

わりとノイズが乗っていますが、きちんとCHSH不等式を破っています。なんか怪しい気もしますが、疲れたので終わりです。
実験用コード
GitHubにコードを置いておきます。src/experiments.pyを実行すると量子コンピュータ上で実験が始まります。でも実行する前にIBM Quantumに登録して、tokenを取得し、IBMQ クラスの save_account メソッドでアカウントを自分のデバイスに登録しておいてください。
https://github.com/msrn-yossy/violation_of_CHSH










Discussion