[Rust] 2Dタイル上での可視性チェック
Rust でのゲームアルゴリズム開発の記事がシリーズになりつつありますが、今回は2Dグリッドタイル上での可視性チェックがテーマです。
ちょっと意味の分かりにくいタイトルですが、下の gif アニメを見れば何をやりたいのかは一目瞭然でしょう。

この記事は例によって swarm-rs プロジェクトの Wiki を(かなり適当に)翻訳した上で少し肉付けしたものです。
可視性チェックとレイキャスティング
ゲームではプレイヤーから見て柱の陰にあるものを隠したりすることによって状況の不確実性を表現したり、戦略上の面白さを演出したりすることがあります。
日本語での文献があまりないので、どう呼べばいいのか迷いますが、英語では Visibility testing などと呼ばれることが多いようです。
視線は直線ですので、レイキャスティングアルゴリズムでこのようなチェックができます。
一口にレイキャスティングと言っても、障害物の形状をどのようなデータ構造で表現するかによって手法は様々です。
この記事では、上のアニメでも明らかなように、2次元のグリッドタイル上でのレイキャスティングを扱います。ポリゴンで表現された障害物に関しては後述の参考文献が参考になります。
2次元タイル上での可視性チェックはローグライクやストラテジーゲームで研究されてきており、長い歴史があります。
普通であれば自前でアルゴリズムを考える必要はほとんどないと思われますが、 swarm-rs の場合は、エージェントが多数 (数百ぐらい) 同時にシミュレートされるので、パフォーマンス上の要求が高く、独自の最適化を施す必要があります。
レイキャスティングアルゴリズム
ここでは2点間の単純な線形補間を使います。
Bresenham のアルゴリズムと同じ挙動ですが、厳密に言うと Bresenham のアルゴリズムのほうが浮動小数点を使わない分少し高速かもしれません。
use cgmath::Vector2;
fn lerp_i(a: Vector2<i32>, b: Vector2<i32>, f: f64) -> Vector2<i32> {
Vector2::new(
(a.x as f64 * (1. - f) + b.x as f64 * f + 0.5) as i32,
(a.y as f64 * (1. - f) + b.y as f64 * f + 0.5) as i32,
)
}
pub(crate) fn interpolate_i<P: Into<Vector2<i32>>>(
start: P,
target: P,
mut f: impl FnMut(Vector2<i32>) -> bool,
) -> bool {
let start_p = start.into();
let target_p = target.into();
let interpolates = (start_p.x - target_p.x)
.abs()
.max((start_p.y - target_p.y).abs());
if interpolates == 0 {
return f(start_p);
}
for i in 0..=interpolates {
let point = lerp_i(start_p, target_p, i as f64 / interpolates as f64);
if f(point) {
return true;
}
}
return false;
}
lerp_i は Linear interpolation (線形補間) の関数で、結果を integer で返します。
interpolate_i は少々込み入っていますが、引数に [i32; 2] や Vector2<i32> などの様々な型を受け付けるようにするため、 Into<Vector2<i32>> のジェネリック関数にしています。
Midpoint circle algorithm
まず最初に思いつくのは、「視野の範囲」を設定し、その中の全てのピクセルにレイキャスティングを試すということです。
しかし、これは非常に効率の悪い方法です。
視野のピクセル幅を
そこで、 Midpoint circle algorithm によって視野の円の外周に対してレイキャスティングを行うことを考えてみます。
しかし、円の外周をピクセル単位で辿っても、レイキャスティングの光線がチェック漏れを起こすピクセルがあります。

これは レイキャスティングに使っているアルゴリズムが Bresenham 相当であるので、厳密には光線に接触するピクセルを網羅していないのが理由ですが、このアルゴリズムにはもう一つ問題があります。
重複したチェック
上の図を見るとわかりますが、発生源付近の光線は「密」であり、多数の光線が同じピクセルに触れています。
これは重複したチェックがあるということです。
もっとわかりやすくするため、光線を直線ではなく、実際に辿るピクセルを繋いだ折れ線で表現してみます。

さらに、光線がピクセルを辿った回数を全ての光線について加算したものに比例した面積の円をそれぞれのピクセルの上に描画してみます。
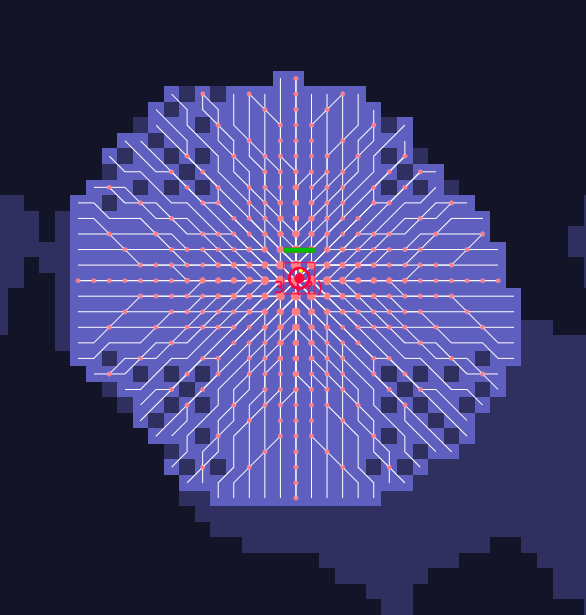
中央付近のピンク色の円の面積が大きいことが分かると思います。
この面積は重複したチェックの回数に比例します。
解決策1: レイキャスティングをやめる
視野の範囲を距離だけでフィルタする方法です。
非常に簡単で高速ですが、障害物の影も見えてしまうというのはやはりリアリティに欠けますし、面白くありません。

解決策2: グラフ探索を行う
レイキャスティングを光線1本ごとに行うのではなく、同じピクセルを通る光線の共通部分をツリー構造のグラフにして重複を減らす方法です。
ツリーのノードが障害物であれば、その全ての子孫ノードを不可視と判定できます。

重複するチェックを削減する効果は非常に高いのですが、実は厳密なレイキャスティングと同じ結果にはなりません。
同じピクセルを通る光線でも、最終地点のピクセルが異なる場合があるためです。
この方法だと、実質的に45度単位の角度の光線のレイキャスティングになってしまいます。
無いよりはましですが、リアリティはあまり感じられない不可視チェックになってしまいます。
解決策3: 逆引きマップのキャッシュ
さて、やはり正確性を期すなら範囲内の全てのピクセルにレイキャスティングを行うことを避けるわけにはいかないようです。しかし
第3の解決策は、逆引きマップをキャッシュするという方法です。
ここでは「マップ」という用語はピクセルを入力とし、ピクセルの集合を返す関数として使います(地図ではありません)。
「順方向マップ」と「逆引きマップ」は次のように定義します。
- 順方向マップ: 与えられたピクセルからそこに至るまでの光線の辿るピクセルを返す。レイキャスティングと同じ。
- 逆引きマップ: 与えられたピクセルが障害物だった場合に隠すピクセルを返す。
順方向マップはレイキャスティングアルゴリズムで陽に求めることができますが、逆引きマップは簡単には計算できません。しかし、あらかじめ計算してキャッシュしておけば毎回再計算する必要はありません。
このキャッシュは視野範囲が同じであれば使いまわせますので、 swarm-rs のように多数の同等なエージェントが登場するゲームでは効率が高いです。
さらに、このマップは90度回転対称性があるので、全方位の4分の1のメモリで記憶できます。[1]
具体的には、次のような関数で順方向マップと逆引きマップを同時に計算できます。
pub(crate) fn precompute_raycast_map(range: usize) -> (Vec<Vec<[i32; 2]>>, Vec<Vec<[i32; 2]>>) {
let mut backward = vec![vec![]; range * range];
let mut forward = vec![vec![]; range * range];
for y in 0..range as i32 {
for x in 0..range as i32 {
interpolate_i([0, 0], [x, y], |p| {
backward[p.x as usize + p.y as usize * range].push([x, y].into());
forward[x as usize + y as usize * range].push(p.into());
false
});
}
}
(backward, forward)
}
これは
実際のチェック時にはレイキャスティングはせず、メモリ上の逆引きマップに従ってピクセルを塗りつぶすだけなので、レイキャスティング自体の効率はそれほど影響しないというのも良いところです。限界効率を求めて Bresenham のアルゴリズムを実装したりする必要はありません。
実際のチェック時のアルゴリズムのコアとなる部分は次のようになりますが、回転対称性をループで処理したりしているため少々込み入っています。
let mut visibility_map = vec![true; VISION_RANGE_FULL * VISION_RANGE_FULL];
for yf in 0..VISION_RANGE_FULL {
let y = yf as i32 - VISION_RANGE_I + 1;
for xf in 0..VISION_RANGE_FULL {
let x = xf as i32 - VISION_RANGE_I + 1;
if VISION_RANGE_I * VISION_RANGE_I < x * x + y * y {
visibility_map[xf + yf * VISION_RANGE_FULL] = false;
continue;
}
let pos = pos_i + Vector2::new(x, y);
let res = game.is_passable_at(pos.cast::<f64>().unwrap().into());
if !res && visibility_map[xf + yf * VISION_RANGE_FULL] {
visibility_map[xf + yf * VISION_RANGE_FULL] = false;
let ray_inverse = &game.fog_raycast_map
[graph_shape.idx(x.abs() as isize, y.abs() as isize)];
for ys in [-1, 1] {
if ys * y < 0 {
continue;
};
for xs in [-1, 1] {
if xs * x < 0 {
continue;
};
for &[jx, jy] in ray_inverse {
let jxf = (jx * xs + VISION_RANGE_I - 1) as usize;
let jyf = (jy * ys + VISION_RANGE_I - 1) as usize;
visibility_map[jxf + jyf * VISION_RANGE_FULL] = false;
}
}
}
}
}
}
この逆引きマップを可視化するのは少々難しいのですが、障害物のピクセルが背後のどのピクセルを隠しているかを線でつないで表現すると下図のようになります。

実行速度と正確性の両方を実現できるので、最終的にはこの解決策を使うことにしました。
さらなる最適化: 位置が同じだった場合の可視性マップキャッシュ
実行速度は、私の環境で 15 ピクセルの半径の視野範囲では、エージェント1体あたり80マイクロ秒ほどです。

これでは数百体のエージェントをリアルタイムでシミュレートして 60fps を出すには十分とは言えませんが、実際にはもう一段の最適化を施しており、ピクセルをまたいだ時のみ可視性チェックの再計算を行っています。
この結果10マイクロ秒ほどになりました。

参考文献
ポリゴンで表現された障害物に対する可視性チェックは、このページが参考になります。
Bresenham アルゴリズムと raycasting の違いについては、こちらが参考になります。
おまけ
解決策とはまったく関係ないのですが、レイキャスティングを可視化する際、面白い目の錯覚を発見しました。
全ての光線は直線のはずなのですが、2つの光源からの光線をプロットすると曲がって見えます。
これはへリング錯視やヴント錯視といわれるものに似ていますが、厳密に分類され名前がついているのかどうか、よくわかりません。

-
厳密には対称行列のような鏡像対称性もあるので、さらにメモリ使用量を削減することも可能ですが、メモリ上の配置が2次元グリッドにならないとアドレス計算が煩雑になるので、むしろ遅くなる可能性もあります。 ↩︎
Discussion