🌊

[Rust] 粒子ベースの流体シミュレーション

2023/10/22に公開

Rust

最近自動微分にはまりすぎなので、少し別のトピックをやりたいと思います。

以前、流体シミュレーションを Rust で書いてみるという記事を書きました。この時は空間上に固定したグリッド上でのシミュレーションでしたが、もう一つの流派があり、流体の要素を粒子で代表させるというものです。前者はオイラー法 (Eulerian method) 、後者はラグランジュ法 (Lagrangean method) とも呼ばれます。時に、この動画で Unity でラグランジュ法の流体シミュレーションで遊んでいるのを見てしまったので、これはもちろん試してみるしかないでしょう。

いつも通りリポジトリはこちらです。

https://github.com/msakuta/rushydro

ブラウザ版はこちらです。

https://msakuta.github.io/rushydro/

オイラー法とラグランジュ法

一言で言うと空間上の格子に注目するのがオイラー法、媒質の動きに注目するのがラグランジュ法です。
英語版 Wikipedia のアニメーションが一目瞭然で分かり易いです。

物理モデル

流体を粒子の集まりと見なす最大のメリットは、ニュートンの方程式が直接適用できることです。これでオイラー法のような移流や発散の除去といった数値計算上のトリックを駆使しなくてもそれなりに安定したシミュレーションができます。ここで最も役に立った参考文献は ^[1] でした。

反発力

液体のように界面のある流体はある意味極端に圧縮性があるといえます。オイラー法は非圧縮性流体のシミュレーションに向いていますが、海面の表現は苦手です。これに対し、ラグランジュの方法なら粒子の密度によって直感的に流体の密度が表現できます。密度と圧力の相関を表現するため、粒子が近づきすぎたら、距離を離すように力を与える必要があります。

粒子の間にかかる力を次のようにモデル化します。等方的な粒子を想定し、力は粒子の相対位置ベクトルの方向のみに働き、その絶対値は距離のみの関数であるとします。式で書くと $i$ 番目と $j$ 番目の粒子の間の力は次の $F_{ij}$ のようになります。

F_{ij} = f(|| \vec{p_i} - \vec{p_j} ||) \frac{\vec{p_i} - \vec{p_j}}{|| \vec{p_i} - \vec{p_j} ||}

ここで $f(x)$ を次のように定義します。 $a$ は吸引力を調整するパラメータです。

f(x) = -(1 - x)^2 - a

この関数は次のようなポテンシャル関数の勾配と考えることができます。Sebastian Lague の動画ではポテンシャルを最初に定義してからその勾配を求めていましたが、我々は上手くいきそうな力を求めてからそれを満たすポテンシャルを求めるという逆の方針で決めています。

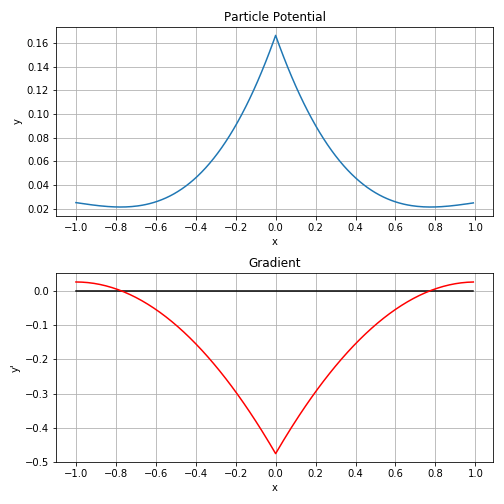
ここで、 $a$ というパラメータは分子間力あるいは表面張力を表現するためのもので、効果としては粒子を引き合わせる吸引力として働きます。反発力は粒子が縮退しないように距離を保つために重要であるので、吸引力は反発力よりもだいぶ弱く(0.05ぐらい)に設定してあります。遠ざかると吸引力が優勢になるので、一定の距離で安定するということになります。ポテンシャルのグラフ上でも、±0.8ぐらいの距離でゆるやかな谷間になっていることが見て取れます。これが流体の自然な密度です(外力によってこの密度にならないことはありますが)。

この吸引力が低いと、サラサラな砂のような流体になり、高いと水のように玉になりやすい流体になります。

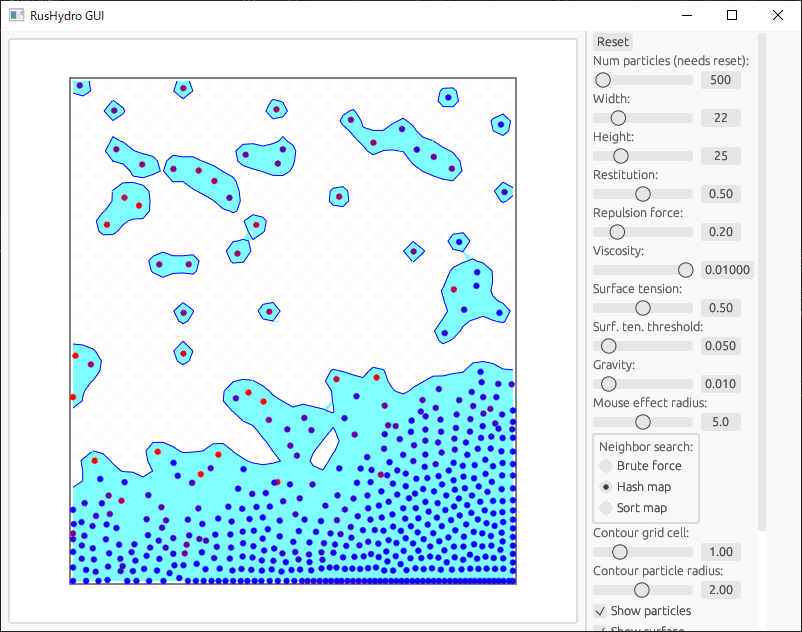
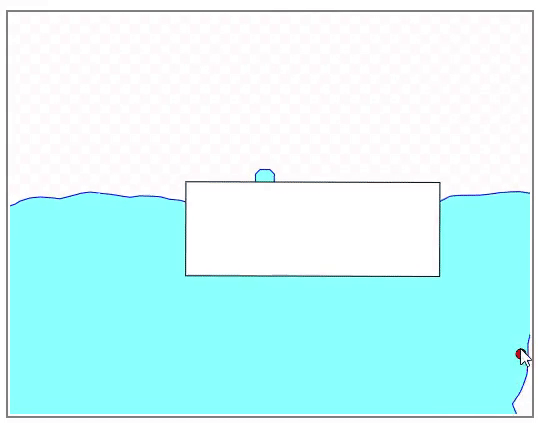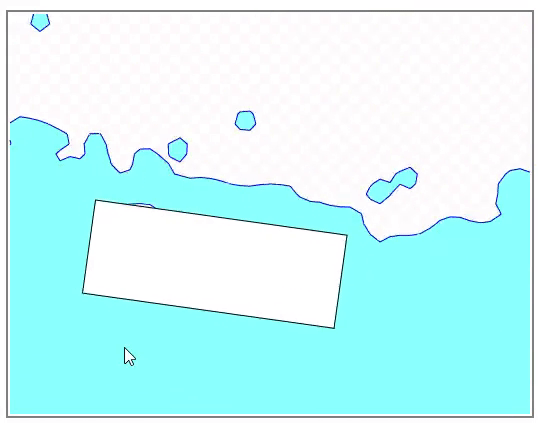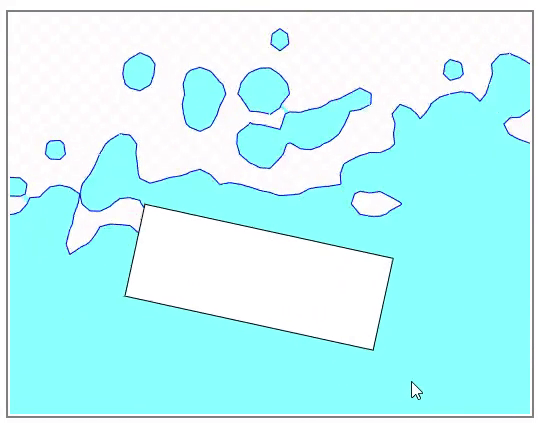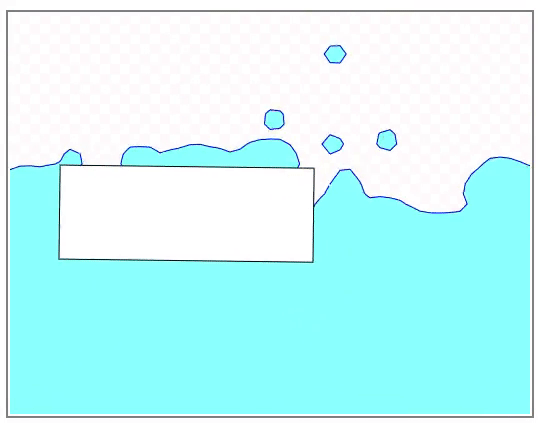
このポテンシャル関数についてはまだ少し気に入らないところがあります。それはほとんど圧縮されないはずの液体が空気のように大きく圧縮されてしまうことがある点です。これは特に下図のような深い液体の底と表面の間で顕著に表れます。ポテンシャルの形がソフトな制約であるためです。

しかし、単にポテンシャルの壁を高くするだけでは解決しません。反発力を大きくしすぎるとシミュレーション自体が不安定になるからです。これは上の図の液体の底にも赤い粒子(速度が大きい粒子)がランダムに表れていることからも見て取れます。静かに置かれているだけの液体でこのような大きな速度が生じるのはシミュレーションの不安定性によるものです。

シミュレーションの安定性についてはオイラー法でも問題になりました。これについては専門外ですが様々な研究があるようなので改善できるかもしれません。

粘性

粘性 (Viscosity) はオイラー法でも出てきましたが、ラグランジュ法では極めてシンプルです。近くの粒子の間に働く摩擦と考えることができます。具体的には、粒子 $i$ と $j$ に働く粘性の力は、平均速度へと近づける向きの力になります。

V_{ij} = \frac{\vec{v_i} + \vec{v_j}}{2} - \vec{v_i}

粘性が高いと、どろどろな流体になり、低いと気体のように媒質が動きやすい流体になります。ここで、相対速度が低下するということは、運動エネルギーが失われるということになるので、激しくかき回してもすぐに静かに落ち着くという形でも観察できます。失われたエネルギーがどこへ行くのかというと、現実の流体では熱になりますが、このシミュレーション上では温度の概念はありませんので、無へ帰します。

固体との相互作用

長方形の剛体と相互作用する機能を付けました。 Environment に None 以外を選ぶと何らかのオブジェクトが現れ、流体の流れに影響します。

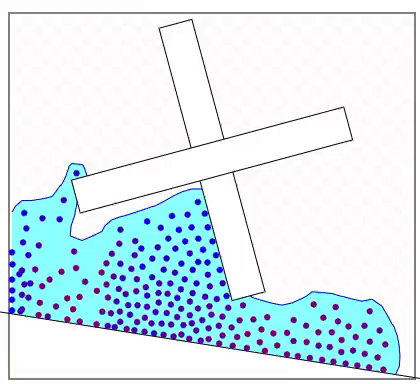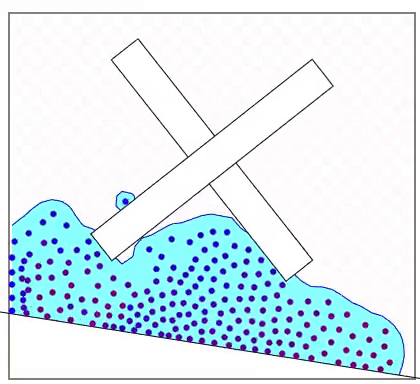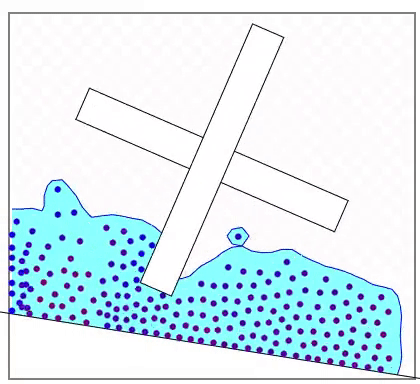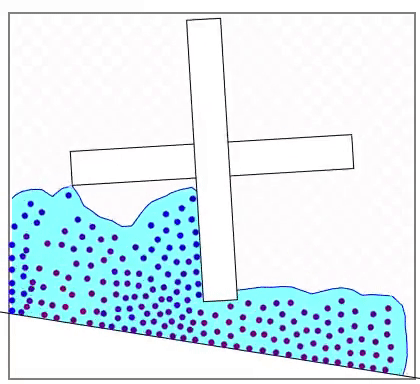
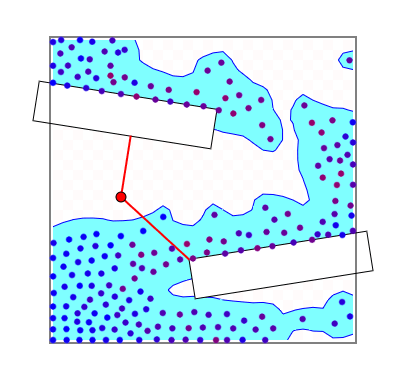
ここでは単純に粒子と物体が接触した場所と速度で反発する衝突検出を行います。このために必要なのは任意の位置から物体への最短距離の計算(負の距離を含む)と法線ベクトルです。法線ベクトルは衝突によって加わる力(瞬間的には運動量)の向きを決めるのに使います。粒子はこの法線ベクトルの方向に運動量を受け取り、物体はその逆方向の運動量を受け取ります。ただし、物体には空間に固定されているものがあり、それに関しては速度は影響しません。

下図は赤い点からのそれぞれの物体の最短距離とその方向ベクトルを示します。方向ベクトルは法線として使われます。

近傍探索の最適化

多数の粒子のシミュレーションですから、素直に相互作用を計算すると全ての粒子の組み合わせを考慮する必要があり、 $O(n^2)$ となります。これは粒子の数が増えると非常に非効率的です。 rushydro ではパフォーマンス比較用に BruteForce 近傍探索モードとして実装してありますが、実用上は何らかの最適化が必要です。

まず、粒子そのものの型は次のようにシンプルに定義されています。

pub(super) struct Particle {
    pub pos: Cell<Vec2>,
    pub velo: Cell<Vec2>,
}

位置と速度が状態になりますが、 Cell で包んでいるのはなぜかというと、同じ Vec コンテナ内の2つの粒子の相互作用を計算するためです。 Cell に包まないと更新ロジックでコンテナの可変参照 &mut を使ってループする必要があり、内部で他の粒子を参照することができなくなってしまいます(可変参照を持つ変数は不変参照すらもできなくなるため)。 Cell であれば不変参照で2重ループにし、内部の値を入れ替えることで内部可変性を実現することができます。しかも Cell には RefCell と違って実行時オーバーヘッドがありません。

これが可能なのは Vec2 型が Copy であり、小さな型だからです。大きな型や複雑な型で Copy になれないものは RefCell に包む必要があり、実行時オーバーヘッドが生じます。しかし、ここでは粒子という非常にプリミティブな型を扱っているので、 Cell が適しています。

これで、 BruteForce 法は次のように2重ループで実装できます。

for (i, particle_i) in self.particles.iter().enumerate() {
    for (j, particle_j) in self.particles.iter().enumerate() {
        if i == j {
            continue;
        }
        Self::update_speed(particle_i, particle_j, &self.params);
    }
    Self::update_speed_from_obstacles(
        &mut self.obstacles,
        particle_i,
        &self.params,
    );
}

グリッドインデックス

最も素直な最適化手法は、グリッド上のセルに含まれる粒子を覚えておくという方法でしょう。 rushydro では HashMap モードとして実装してあり、デフォルトの方法です。

オプションの Show grid と Show grid count で次のようなデバッグ表示ができます。それぞれの赤い正方形がグリッドのセルを表し、中の数字がそこに含まれる粒子の数を表します。

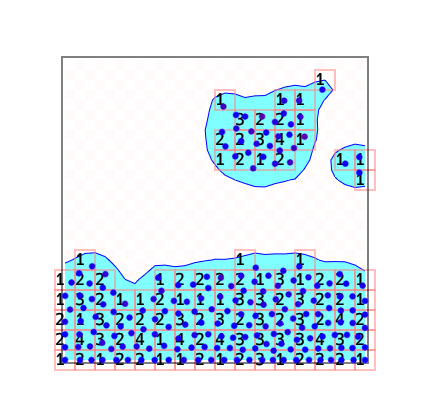
コンテナとしてはグリッドをフラット化した Vec<Vec<usize>> でも良いですが、半分以上のセルは空であることが多いので、ここでは HashMap<(i32, i32), Vec<usize>> を使っています。

ソートマップ

Sebastian Lague の動画では、グリッドを確保する別の方法が採用されています。 GPU にロジックを移行するという目的のため、動的メモリを使わないデータ構造を使用しています。ここでは便宜上ソートマップと呼称します。

これは中々スマートな方法で、 HashMap のバケットの代わりにメモリ上の連続したインデックスを用い、その先頭へのインデックスを持っておくという方法です。詳しくは動画の 23:30ごろからを参照してください。

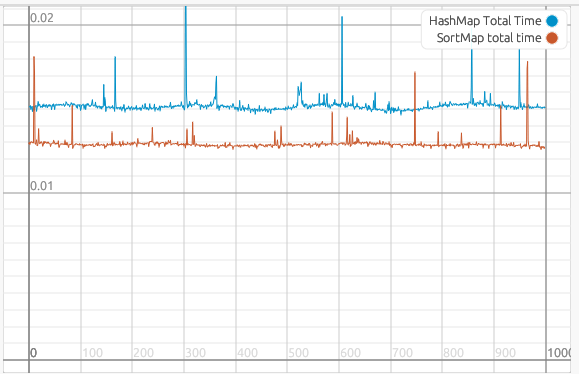
速度を 15000 個の粒子で計測したところ、私の環境では HashMap より少し速いぐらいになりました。 14-16ms ぐらいなので 60fps のレンダリングには間に合うかどうかぎりぎりといったところです。

レンダリング

rushydro は eframe/egui を用いており、あまり高度な描画はできません。それでも最低限液体に見えるようにするため、 Marching squares を用いて粒子の密度の高いところを塗りつぶしています。

この塗りつぶしの視覚的効果は劇的で、これがないとパチンコにしか見えません ^^;

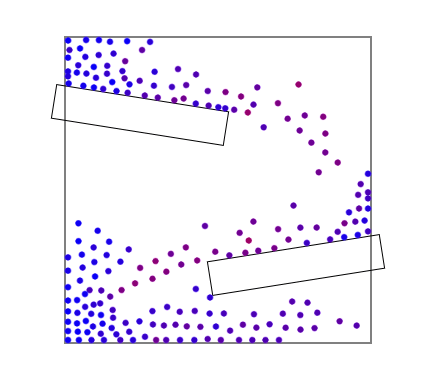
Marching squares についてはよく知られているアルゴリズムなので、内容は説明しませんが、基本的には粒子の密度を2次元グリッド上に書き込んで等高線を引いていると考えればおおむね正しいです。

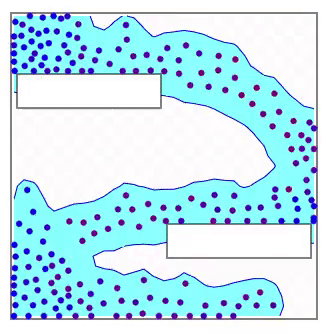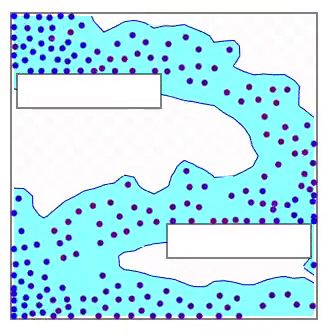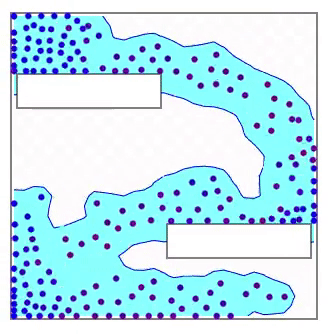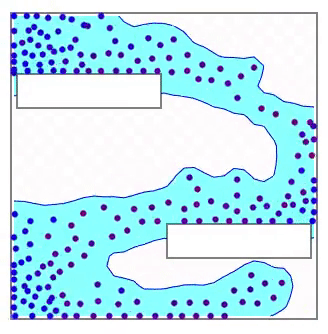
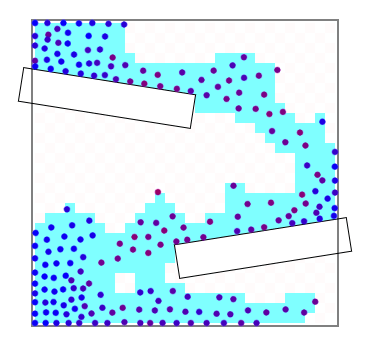
塗りつぶしについてはちょっとしたトリックを使っています。 Marching squares は境界を描画するアルゴリズムですので、そのままでは効率的な塗りつぶしはできません。例えばグリッドのセルを一つずつ正方形のプリミティブで描画するなどの方法では大いに無駄があります。そこで背景に画像を描画し、塗りつぶせるピクセルは画像のピクセルとして水色を配色します。境界を取り除けば画像は下図のようになります。

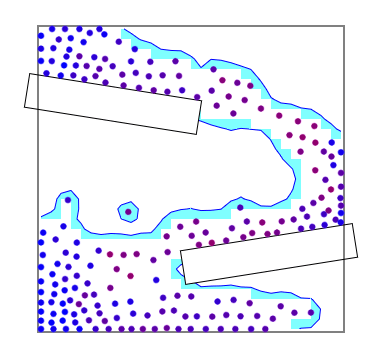
この上に境界となるピクセルの内部を描画します。ただし、ピクセルの中でも液体の内部の側には塗りつぶしが必要ですので、ポリゴンの塗りつぶしをしています。背景の画像を取り除くと下図のようになります。

この2つを組み合わせることであたかも内部が塗りつぶされた大きな液体の表面を最小限のプリミティブでレンダリングすることができます。

今後の展望

今までのところ上手く動いていると思いますが、いくつか課題があります。

液体の圧縮性の問題。これについては ^[2] が参考になるかもと思っていますがまだ読み込んでいません。
GPU への移行。並列性の高い部分とそうでない部分があるので、簡単ではないと思われますが、数万以上の粒子にスケールするためには必要です。
固体の衝突・反発物理シミュレーションの改善。特に固体同士の衝突検知はまったくできていません。
Ray marching による3次元レンダリング。

脚注

Dan Koschier1, et al. Smoothed Particle Hydrodynamics Techniques for the Physics Based Simulation of Fluids and Solids ↩︎
Jos Stam, Stable Fluids, https://www.researchgate.net/publication/2486965_Stable_Fluids ↩︎