Python微分演算子の行列表現

目的

下記のようにデータが一定のサンプリング間隔のNumPy配列で与えられているとき、これを数値的に微分するための行列を求める。

$$\bold{y} = \left[ \begin{matrix} y_0 \\ y_1 \\ \vdots \\ y_{n-1} \end{matrix} \right]$$

$x$のサンプリング間隔$\Delta x$は一定で、$\bold{y}$は列ベクトルと仮定している。

数値差分の方法

前進差分を用いると、下記のように微分を数値的に計算できる。

$$y'_n=\frac{y_{n+1}-y_n}{\Delta x}$$

これを行列で表せば、下記のようになる。

$$D_1=\frac{1}{\Delta x}\left[\begin{matrix} -1 &1&0&\dots0&0\\ 0&-1 &1&\dots0&0\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0&0 &0&\dots-1&1\\ 0&0 &0&\dots0&0\\ \end{matrix}\right]$$

微分演算子行列$D_1$を用いると、微分結果を格納したベクトル$\bold{y'}=(y'_{0},...,y'_{n-1})^T$は下記のように計算できる。

$$\bold{y'}=D_1\bold{y}$$

ただし、周期境界条件などを仮定しない限り、差分行列の最後の要素$y'_{n-1}$は正しく計算できないので注意を要する。

Pythonコード

import numpy as np
import matplotlib.pyplot as plt

def get_d1_matrix(n: int, dx: float) -> np.ndarray:
    diag_elements = np.diag(-np.ones(n))
    non_diag_elements = np.roll(np.diag(np.ones(n)), 1, axis=1)
    non_diag_elements[-1, 0] = 0
    d1_mat = diag_elements + non_diag_elements
    d1_mat[-1, :] = 0
    return d1_mat / dx

n = 10
dx = 0.1
d1_mat = get_d1_matrix(n, dx)

plt.title(r'$D_1$')
plt.imshow(d1_mat)
plt.colorbar()
plt.show()

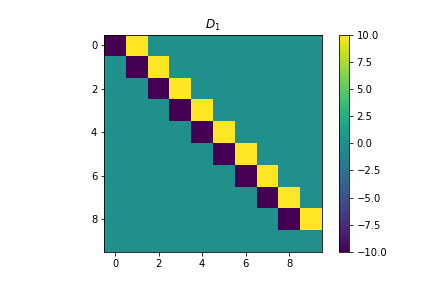
例

例として$y=\sin x \cdot e^{-ax}$の微分を計算する。
この関数は解析的にも$y'=(\cos x -a \sin x) e^{-ax}$のように微分できる。
行列演算子を用いて数値的に求めた解と、解析に求めた解を比較する。

n = 200
dx = 0.1
x = (np.arange(n) * dx)[:, None] # 列ベクトルにする

a = 0.1
y = np.sin(x) * np.exp(-a * x)

# 微分演算子行列を用いて、微分を計算
d1_mat = get_d1_matrix(n, dx)
y_diff_numerial = d1_mat @ y

# 解析的に微分を計算
y_diff_analytical = np.cos(x) * np.exp(-a * x) - a * np.sin(x) * np.exp(-a * x)

plt.figure(figsize=(6.4 * 2, 4.8))
plt.subplot(121)
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.subplot(122)
plt.plot(x, y_diff_numerial, label='numerial')
plt.plot(x, y_diff_analytical, label='analytical')
plt.xlabel('x')
plt.ylabel("y'")
plt.legend()
plt.show()

左は微分前の関数を示したグラフで、右が微分結果を示したグラフである。右図の青が微分演算子を用いて数値的(numerical)に計算した結果で、オレンジが解析的(analytical)に計算した結果である。境界を除いてよく一致していることがわかる。