Kaggleメダル獲得への挑戦 Vol.2
はじめに
この記事は30歳未経験からエンジニアに転身したド文系の僕が、機械学習エンジニアになるためにKaggleに挑戦しながらスキルを身につけていく過程をリアルタイムで発信していく連載記事となります。
毎週末、その週に僕自身が学んだ内容を発信していきます。
学びながら発信していきますので、場合によっては間違った情報や、誤って理解してしまっているものもあるかもしれません。
その際はぜひ温かくご指摘をいただけるとうれしいです!
ド文系でも本気で取り組めば結果を出せるんだという姿を見せられるように、日々頑張っていきます!
2025年5月5日〜5月11日までの学び
注)Kaggleは英語で構成されているため、その用語に慣れるためにも、主要な用語は英語のまま学ぶこととしています。
なので以下の記事でもところどころ英語のまま記載していますが、それは上記の意図があって敢えてそう表記しているものなので、その点だけご理解ください。
linear relationship
日本語では「線形関係」
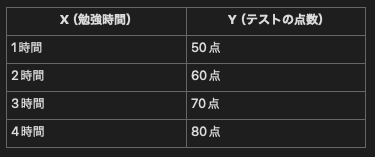
入力(X)が変わると、それに比例して出力(Y)も変わる関係のことを指す
つまりXとYの間に、直線的な関係(比例した動き)があるという意味
具体例
機械学習ではどのように使われるか?
・Linear Regression(線形回帰モデル)
→線を引いて予測するモデル
→「線形関係がある」と仮定して、最適な直線(Y = aX + b)を探す
・Feature ValueとTarget Valueの関係を探るとき
→Feature ValueとTarget Valueの間にlinear relationshipが強いと、シンプルなモデルでも高い精度が出やすい
→特に線形モデル(Linear Regression、Logistic Regression)では、linearなFeature Valueがあるかどうかが超重要
その他備考
・Positive linear relationship: Xが増えるとYも増える(右上がり)
・Negative linear relationship: Xが増えるとYは減る(右下がり)
・No linear relationship: XとYに直線的な関係はない(つまりぐちゃぐちゃ)
XGBoost
XGBoost(eXtreme Gradient Boosting)という強力な機械学習モデルの「回帰用クラス」
特徴
・高速かつ高精度
→多くのKaggle優勝者が使うモデル
・勾配ブースティング
→弱い木を多数組み合わせて強力な予測にする
・欠損値処理が強い
→欠損値があっても自動で補完処理する
・正則化あり
→過学習にも強い
使う場面の例
・家の価格予測
・売上予測
・需要予測
・医療・金融・マーケなど
pythonでのimport文
# Regressorは数値を予測するための関数
from xgboost import XGBRegressor
# XGBClassifierは分類タスクをこなす関数
from xgboost import XGBClassifier
交差検証とは?
→データを複数に分けて、その回数分モデルを作成し精度を平均化する手法
→例えば5分交差検証であれば、データを5つに分けて、5回モデルを作成し精度を平均化する
なぜ交差検証が必要か?
単純な「訓練データ/テストデータ」の分類では、分割の運が悪いと変な精度が出るため、評価がぶれやすい
イメージ的には以下のような感じ
全データ → [ Fold1 | Fold2 | Fold3 | Fold4 | Fold5 ]
1回目:Fold1 = テスト、残り = 訓練
2回目:Fold2 = テスト、残り = 訓練
...
5回目:Fold5 = テスト、残り = 訓練
→5回テストして平均を取る=より信頼性の高いスコアが得られる
pythonではcross_val_score()という関数で実装可能
score = cross_val_score(
# cv=5がCross Validation(交差検証)回数
model, X, y, cv=5, scoring="neg_mean_squared_log_error",
)
MAEとは?(Mean Absolute Error)
→予測値と実際の値のズレの「大きさ」を測るシンプルで直感的な指標
→回帰モデルの精度を評価する際によく使われる
MAEの特徴
・誤差の扱いは絶対値→直感的に差が理解しやすい
・単位も元の単位と同じ→外れ値に対する影響は小さい
MAEが使用される場面
・回帰モデルの評価
→住宅価格、売上予測、需要予測などで「予測のズレを平均的にどれくらい許容できるか」を測る。
・外れ値をあまり重視したくないケース
→MSEだと一部の外れ値がモデル全体を狂わせるが、MAEなら影響が小さい
・ビジネス上、「ズレ幅そのもの」に意味があるケース
→例えば「1商品あたり予測と実績の差が何円か」が知りたい時
MSEとは?(Mean Squared Error)
・「予測値と実際の値がどれだけズレているか(=誤差)」を測る代表的な指標
・特に回帰モデルの性能評価において最も基本的でよく使われる評価指標のひとつ
・誤差(予測 − 実測)を二乗して、それらの平均を取ったもの
MSEの特徴と意味
・二乗している→大きな誤差を強くペナルティ(=外れ値に敏感)
・符号が消える→負の誤差と正の誤差が打ち消し合わない
・平均をとる→データ全体のズレの平均を見ている
・単位が元の二乗になる→例:円 → 円²、kg → kg²
なぜ誤差を二乗するのか?
・正負の誤差がキャンセルされないようにする
・小さな誤差より大きな誤差にペナルティをかけたい
→例:10の誤差 → 100(10²)、100の誤差 → 10,000(100²)
MSLEとは?(Mean Squared Logarithmic Error)
・「予測値と実際の値の"Log(対数)"の差を二乗して平均した誤差」
・MSLEは「何倍ずれたか?」を敏感に検知可能=特に小さい値の予測精度を重視したい時に向いている
RMSLEとは?(Root Mean Squared Logarithmic Error)
→「MSLEの平方根」=より直感的に理解できる誤差指標
→「誤差のスケール」が元の単位に近くなるため、人間が解釈しやすい
なぜLogを使うのか?
・Logをとると「相対的なズレ」がわかる
通常の誤差(MSE)などは「絶対的なずれ(いくらずれているか)」を重視するが、Logを使うと「何倍ずれているか?」=相対誤差を検知することができる
以下、具体的数値で比較→ 同じ絶対誤差(10)でも、実際の値が小さい値ほどlog誤差が大きくなる
つまり、小さな値の予測ミスをより厳しく評価する性質がある
なぜLogが便利か?
例えば、
・不足や売り切れが命取りな在庫予測では「10個」の差は非常に重要
・一方、住宅価格での「10万円」は誤差の範囲なのであまり大きな問題ではない
→Logを使うと、対象領域に応じた実質的ズレに注目できる
そしてMSLEは「真の値と予測値の比率(何倍違うのか?)のLogを見ている
具体例
・真の値:10、予測:20(2倍ズレ) → log(2) ≈ 0.69
・真の値:100、予測:200(2倍ズレ) → log(2) ≈ 0.69
・真の値:1000、予測:2000(2倍ズレ) → log(2) ≈ 0.69
→ 「2倍ズレ」がどんな値でも同じように扱われるという対称性がある
これは 絶対誤差(1000 vs 10)に比べて、はるかにバランスが良い
RMSLEは、対数誤差(MSLE)の平方根をとることで、Logのスケールから元のスケールに近づけることができる
MSLE・RMSLEを使うべき判断基準(どんな時に選ぶか?)

各指標のまとめ

これから過去コンペなどに挑戦し、どの指標を使えばいいかの肌感覚は手を動かしながら磨いていくこととする
ワンホットエンコード
→カテゴリ(文字列)データを機械学習モデルが扱える数値データに変換する手法の一つ
なぜワンホットエンコードが必要か?
・機械学習モデル(特に回帰やツリー系のモデル)は、文字列のままでは学習できない
・しかし、単純に A=1, B=2, C=3 などと数字を割り当てると、順序や大小を誤解してしまう
→この問題を防止するために、それぞれのカテゴリごとに別の列(カラム)を作り、「そのカテゴリだけ1、他は0」とするのが「ワンホットエンコード」
👇ワンホットエンコードのコーディング例
import pandas as pd
df = pd.DataFrame({'色': ['赤', '青', '緑', '赤']})
pd.get_dummies(df, columns=['色'], prefix='色')
# 結果
色_赤 色_青 色_緑
0 1 0 0
1 0 1 0
2 0 0 1
3 1 0 0
ワンホットエンコードのメリット・デメリット
メリット
・モデルがカテゴリ情報を誤解しない
・ツリー系モデルにも有効
・実装が簡単
デメリット
・カテゴリ数が多いと「列数が爆発する」
・スパース(0が多い)になる
unsupervised learning algorithms(教師なし学習)
・正解ラベル(答え)が存在しないデータに対して、その中に潜む構造やパターンを見つけ出す機械学習の手法
・教師なし学習では「入力(特徴量)」だけを使って学習を行い、データの中にある位規則性・構造・グループ分けなどを自動で見つけ出す
教師あり学習
入力+正解(ラベル)で学習→価格や種類などを予測する際に使用
教師なし学習
入力のみで学習。正解はなし→クラスタ分け、特徴抽出、異常検知などをする際に使用
代表的なUnsupervised Learningアルゴリズム
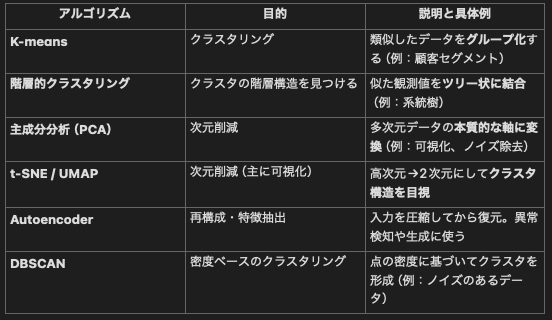
Unsupervised Learningが使用される場面

K-mean Clustering
・データをあらかじめ指定したK個のCluster(グループ)に分割し、各クラスタのcentroids(重心)を元にデータを分類するアルゴリズム
・Kは分類したいClusterの数、meansは各Clusterの中心(mean = 平均)を求めることに由来
K-meansアルゴリズムの流れ
- 初期化
ランダムにK個のcentroidsを選択 - Assignment
各データを最も近いcentroidに割り当て(ユークリッド距離などを使用) - Update
各Cluster内のデータ点の平均を取り、centroidを再計算 - 収束判定
centroidがほとんど動かなくなるまで2と3を繰り返す(もしくは指定した最大ステップ数に達する)
K-meansの用途(具体例)
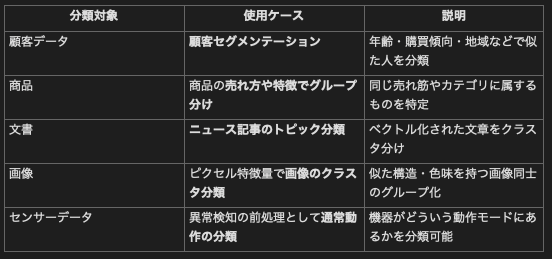
K(Cluster数)をどのように選ぶか?
K-meansクラスタリングを使ううえで 「K(クラスタ数)をいくつにすべきか?」は非常に重要なテーマ
Kを適切に選ばないと、分類が粗すぎたり細かすぎたりして、意味のあるグルーピングができない
・Kが少なすぎると、異なるグループが1つにまとめられてしまう
・Kが多すぎると、同じグループが無理やり細分化されてしまう
・正しいKは、「本質的な構造に最も近い」Cluster数
Kの数の選び方
Elbow法
・各Kに対して「クラスタ内誤差の総和(SSE)」を計算し、K vs SSE のグラフを描く
・SSEが急激に減少しなくなるポイント(ひじ=Elbow)をKとする
・Kを増やすほどSSEは必ず下がるが、ある地点からは効果が薄れる
・その「曲がり角」が適正なK
👇pythonの具体的コード
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
# Xは特徴量が格納されたDataframe
sse = []
for k in range(1, 11):
kmeans = KMeans(n_clusters=k, random_state=42)
kmeans.fit(X)
sse.append(kmeans.inertia_) # SSE(inertia_)
plt.plot(range(1, 11), sse, marker='o')
plt.xlabel("Number of clusters")
plt.ylabel("SSE (Inertia)")
plt.title("Elbow Method")
plt.show()
シルエットスコア
概要:
・各データ点に対し、「同じクラスタとの近さ」 vs 「他クラスタとの距離」を比較してスコア化
・スコアは -1 ~ 1:高いほど良いクラスタリング
評価基準:
・0.7〜1.0 → 非常に明確なクラスタ構造
・0.5〜0.7 → 良いクラスタ構造
・0.25〜0.5 → 微妙
・< 0.25 → あまり分かれていない or Kが合ってない
👇pythonの具体的コード
from sklearn.metrics import silhouette_score
for k in range(2, 11):
kmeans = KMeans(n_clusters=k, random_state=42)
labels = kmeans.fit_predict(X)
score = silhouette_score(X, labels)
print(f"k={k}, Silhouette Score={score:.4f}")
おすすめのKの個数決定手順
- Elbow法で候補のKを2〜3個に絞る
- シルエットスコアでその中からベストを選択
- 上記の可視化や意味の解釈を行い、最終判断をする
Scaling
・機械学習において 特徴量(=各列の値)の「大きさ(スケール)」を整える前処理 のこと
・データの値の範囲や単位を揃えて、機械学習モデルが各特徴を平等に扱えるようにする処理
なぜScalingが必要か
・多くの機械学習アルゴリズム(K-means、線形回帰、SVM、KNNなど)は「特徴量同士の大きさの違い」に敏感(以下の例参照)

上記のような身長と年収という2つの特徴量を使用してK-meansでCluster化する場合、そのままの値を使用してしまうと、年収の差がClusteringの際に支配的に利用されてしまう
→年収の差の幅の方が、身長の差分よりも大きいため、身長の差分はClusteringの際にほぼ無視されてしまう
Scalingの目的
・特徴量を同じくらいの大きさに揃える
→アルゴリズムが1つの特徴だけに偏らないようにする
・距離計算が意味あるものになる
→K-meansやKNNなどは「距離」に基づいて判断する
・勾配が安定して学習が早くなる
→ニューラルネットや戦型会期の最適化が早くなる
主なScaling手法

Scalingが必要な代表的なアルゴリズム

K-means Clusteringの具体的ステップ
・使用する特徴量を選択する
→目的にあった定量的(数値型)な特徴量を選択する
例)
顧客データの場合:年齢、購入頻度、平均購入金額
商品データの場合:価格、レビュー数、評価
都市データの場合:平均気温、降水量、標高
・Scalingで単位を揃える
→各特徴量のScale(値の大きさ)を揃えることで、特定の特徴だけが影響を与えるのを防止する
※ 距離を使うモデル(K-means、KNN、SVMなど)ではScalingは必須
・Clusteringを実行
fit_predict()で学習&分類を一括で行う
→各行に対してクラスタ番号(0〜K-1)が付与される
・可視化、評価
Elbow法やシルエットスコアなどを使用してCluster数の妥当性をチェックする
👇この手順に沿って作成したサンプルコードが以下
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
# ============================================
# ステップ①:K-meansクラスタリング処理
# ============================================
def perform_kmeans_clustering(df, features, n_clusters=3, random_state=42):
X = df[features]
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
kmeans = KMeans(n_clusters=n_clusters, random_state=random_state)
df["Cluster"] = kmeans.fit_predict(X_scaled)
return df, X_scaled
# ============================================
# ステップ②:クラスタ結果の可視化
# ============================================
def plot_clusters_2d(df, x_feature, y_feature, cluster_col="Cluster"):
plt.figure(figsize=(6, 4))
plt.scatter(df[x_feature], df[y_feature], c=df[cluster_col], cmap="viridis", s=60)
plt.xlabel(x_feature)
plt.ylabel(y_feature)
plt.title("K-means Clustering Result")
plt.grid(True)
plt.show()
# ============================================
# ステップ③:クラスタ数(K)を検討する用関数
# ============================================
def evaluate_k_values(X_scaled, k_range=range(2, 10)):
inertias = []
silhouettes = []
for k in k_range:
kmeans = KMeans(n_clusters=k, random_state=42)
labels = kmeans.fit_predict(X_scaled)
inertias.append(kmeans.inertia_)
silhouettes.append(silhouette_score(X_scaled, labels))
# グラフ描画
fig, ax1 = plt.subplots(figsize=(8, 4))
ax1.plot(k_range, inertias, marker='o', label='SSE (Elbow)', color='tab:blue')
ax1.set_xlabel('Number of clusters (k)')
ax1.set_ylabel('SSE (inertia)', color='tab:blue')
ax1.tick_params(axis='y', labelcolor='tab:blue')
ax2 = ax1.twinx()
ax2.plot(k_range, silhouettes, marker='x', label='Silhouette', color='tab:green')
ax2.set_ylabel('Silhouette Score', color='tab:green')
ax2.tick_params(axis='y', labelcolor='tab:green')
plt.title('Elbow & Silhouette Method for Choosing k')
plt.grid(True)
plt.show()
# 結果出力
print("\n▼ Elbow(SSE)と Silhouette スコア一覧:")
for k, sse, sil in zip(k_range, inertias, silhouettes):
print(f"k={k}: SSE={sse:.2f}, Silhouette={sil:.4f}")
if __name__ == "__main__":
# 仮データ(例:顧客データ)
df = pd.DataFrame({
"Age": [25, 45, 30, 50, 27, 60, 35, 40],
"PurchaseFreq": [2, 10, 3, 8, 2, 11, 5, 9],
"Spend": [100, 300, 120, 400, 90, 420, 200, 350]
})
features = ["Age", "PurchaseFreq", "Spend"]
# Step 1: 最適なKを可視化・確認
_, X_scaled = perform_kmeans_clustering(df.copy(), features) # 仮に1回クラスタリングしてX_scaledを取得
evaluate_k_values(X_scaled, k_range=range(2, 8)) # k=2〜8で評価
# Step 2: 実クラスタリング(k=3など)
df_clustered, _ = perform_kmeans_clustering(df, features, n_clusters=3)
# Step 3: 各クラスタの特徴(意味づけ)
print("\n▼ 各クラスタの平均値:")
print(df_clustered.groupby("Cluster")[features].mean())
# Step 4: クラスタの可視化(Age vs Spend)
plot_clusters_2d(df_clustered, "Age", "Spend")
今週の学びは以上です。
次週も頑張って学びを積み上げていきます!
未経験からエンジニア転職を目指すあなたへ
僕は今「未経験から本気でエンジニア転職を目指す人」のための新しいサポートサービスを準備中です。
もしあなたが…
- 業務改善を通じて価値を出せるエンジニアを目指したい
- 数字や仕組みで現場を変える力を、キャリアに活かしたい
- これから学ぶべきステップを明確にしたい
そんな想いを少しでも持っているなら、ぜひ僕の公式LINEに登録しておいてください。
サービスに関する先行案内や最新情報を優先的にお届けします。
👉公式LINEはこちら
Discussion