🔒

楕円曲線暗号によるデジタル署名をふんわり理解する

2022/08/07に公開

ブロックチェーン

もともとBitcoinとかブロックチェーンについて調べていた途中で気になった内容ですが、まとめたら結構な量になってしまったので記事を分割した次第です。
色々ガバガバなはずなので、ちゃんとしたい人は書籍とか読んでください...

デジタル署名って？

秘密鍵（人に教えちゃダメ）と公開鍵（みんなに教える）を用いて、こんな感じのフローで署名が秘密鍵の持ち主本人によるか？とハッシュ値が改竄されてないかを確認します。

上記が検証できれば、次のステップとして内容を検証したいメッセージから算出したハッシュと、署名から検証できたハッシュを突き合わせることで、メッセージ本体が改竄されてないかを確かめることができます。

楕円曲線って？

上記デジタル署名を実現する技術の一つとして楕円曲線暗号というものがあります。
楕円曲線暗号にでてくる楕円曲線は

y^2 = x^3 + ax + b

の形であらわされる実数平面上での曲線を指すと考えてよさそうです。
（ちゃんとした定義は数学書とか読んでください）

式を見てわかる通り、xが負の数の領域では、 $y^2 < 0$ 　となりうるため実平面状では解なしになります。また、 $y^2 > 0$ では、明らかにx軸に対称なy座標2点が解になりえます。

Wikipediaの図を借りるとこんな感じのグラフのようです。
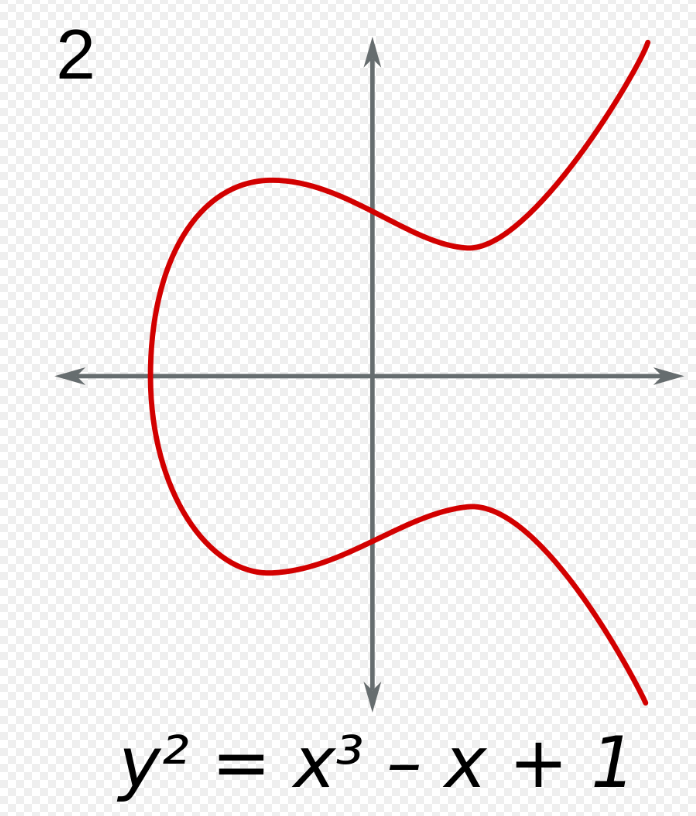
楕円曲線の図
https://ja.wikipedia.org/wiki/楕円曲線　より

楕円曲線と直線の交点と、楕円曲線上での足し算（加法）

さて、次にこの楕円曲線と直線の交わり方についてハチャメチャにざっくり考えていきます。

この楕円曲線と直線 $y=sx + t$ の交点は、 $y^2 = (sx+t)^2 = x^3+ax+b$ の解となります。
（ただし、y=k, x=kのようなx軸y軸に平行な直線の場合は上記代入ができないので上の通りとはならないですね。ほかにも例外ケースある気がしますが細かい場合分けは許して）

ここで、この方程式は3次式なので、解を３つもちます。実数係数方程式が複素数解をもつとき、その共役複素数も解となることを考えると、解のパターンは

 1. 実数3つ
 2. 複素数2つ＋実数1つ

のどちらかになります。ここで、xy平面にある楕円曲線の点G、Hを考えてみるとGとHで実数解2つが埋まっているため（だいたいの場合）GとHを通る直線は、楕円曲線とGとH以外にもう１点で交わることになります。
ところで、G=Hの場合はどうしましょう？その場合はG=Hを通る楕円曲線の接線を利用することにしましょう。この場合も接点（重解）を除いてもう1点で交わることになります。

ここで、次の操作を考えます。

1. 楕円曲線C上の点G,Hがあるとき、G,Hを通る直線lを引く(G=Hの時は接線を利用する）
2. 直線lと楕円曲線Cの交点のうち、G,H以外に新たに得られた点をRとする。
3. Rをx軸対称に移動した点（楕円曲線自体がx軸対称なため、これも楕円曲線上にある）を-Rとする。
（x軸対称なのでy座標しかマイナスになってないですが、-Rと呼んでおきます）

3の対称移動は数学に明るくない私のような人はおまじないだと思ってよいです。
（詳しく知りたい人は「楕円曲線　群」とかでググりましょう）

この対称移動というおまじないをすると、楕円曲線で上の操作をして新しい点を求めるというのと、我々が知っているような足し算は近い性質をもつようになります。

近い性質をもつということなので、G,Hが与えられたとき、1～3の手順で新しい点-Rを得るというのをこう書いちゃいましょう。

G+H = -R

さてG=Hの時は足し算と似ているというのであれば、方程式の時のx+x=2xのように

G+G = 2G

と表記しちゃいましょう。楕円曲線上の点Gから接線を引いて得た新たな交点をx軸対称移動した点を得る。というのはGから2Gを求めることです。

nGにまつわる困難性

ネタバレをすると、楕円曲線暗号ではnGのnを秘密鍵として利用します。すなわちある基準点Gに何回上のループ操作をしたか？というのを秘密鍵とします。
秘密鍵として使う上で、下の二つの困難性を考えてみます。

nとGが与えられたとき、nGを求める。
nGとGが与えられたときnを求める。

ここで、nを160bitの整数としておきます。

nとGが与えられたとき、nGを求める

この計算は結構楽にできます。
$G+G=2G, 2G+2G=4G$ になるため、(2^k)Gは倍々に計算していけば高々k回方程式を解けば求まります。そのため、160bitの整数であっても、kは整数として、

(2^k)Gを( $0<=k<=(nの2進表示桁数)$ の範囲で求める（nが160bitなら160回計算するだけ）。
nの2進表示を順にみていってkbit目が1なら(2^k)Gを答えに加算する（これもnが160bitならMAX160回計算するだけ）

なので、数百×（接線と交点を求める計算）程度の計算量でnとGからnGを求めることができます。
コンピュータにとったら超絶楽勝です。

nGとGが与えられたときnを求める。

こっちはかなり難しいです。（現在は難しいとされています）
楕円曲線で線を引いて交点をとって...というのを何度か繰り返してみるとわかりますが、新しい-Rを取るたびに座標が大きくなったり小さくなったりランダムに遷移します（するように見えます）し、その繊維幅もまちまちです。

即ち、（ある程度楕円とGを慎重に選べば）適当な値sでsGを計算してみても、sを大きくすればnGに近づくのか、小さくすればnGに近づくのかの手掛かりが全く得られないことになります。
手掛かりが全く得られないため、総当たりに近しい方法でしか解くことができません。
比較的効率的に解く方法はいくつかあるようですがそれらもせいぜい、 $\sqrt(n)$ が限度のようです。（ECDLP 計算量とかでググると出てきます）

すなわち、nが160bitの場合は2^80 > 10 ^24回程度の計算をさせることになり、1秒に10^8回程度コンピュータが計算できる仮定では10^16秒 > 3*10^8年程度かかります。
GPU等による並列化、クラウドコンピューティングによる並列化などがあっても依然として解くのが難しいです。

楕円曲線を利用したデジタル署名

やっとたどり着きました。ここまでの話で以下の情報がそろっています。

楕円曲線上で足し算と定数倍算のようなものが定義できる。
点Gの定数倍算nGについて、nとGからnGを求めるのは簡単である。
点Gの定数倍算nGについて、nGとGがわかってもnを求めるのは難しい。

ところで、これまで意図的に無視していましたが、実際はnGのそれぞれの座標は、ある素数pでの剰余として計算していきます。 普通の足し算や掛け算の時を $3+1\equiv 4 \ (mod 5)$ になるように、上の性質については変わらず考えてよいです。（よいと思っています）

さて、あるメッセージに署名をするとき、天下り的に次の値を追加で用意します。

1. q: nGのnのようにGを移動する係数として使う、十分大きい値の中からランダムに選ぶ。
2. h: メッセージのハッシュ値。これが改ざんされていないか知りたい。
3. R : qGのx座標
4. S: (h+nR)/q (mod p)

なんのこっちゃという感じなのですが、楕円曲線暗号では、上のSとRを署名として利用します。
念のため、SとRから秘密鍵の復元性などを確認してみると、

R：無関係なqGから生成されているためここからnは推測不可。またnの秘密鍵の時の議論と同じく、qGの座標がわかってもqを知ることは困難
S：qを知ることが困難である上、qが分かってもそもそもnGからnを求めることは難しいため、Sから秘密鍵nを知ることは困難。またSはランダムに決めたqと秘密鍵nの両方がそろわないと生成できないため、Sの生成も秘密鍵の持ち主しかできない。

となっていて（qに毎回同じ値を使ってしまったりしない限りは）秘密鍵nを推測することは困難なままであることが分かります。

ここで、さらに天下り的ですが、 $hG/S + R(nG)/S$ 　を計算してみます。すると、
$hG/S + R(nG)/S = (h+Rn)G/S = (h+Rn)G・q/(h+nR) = qG$
という関係が成り立ちます。

* 署名値Sの生成は秘密鍵nの持ち主しかできず、またハッシュ値hの情報もSに含まれる。
* ハッシュ値h、プロトコル的に決まる基準点G、署名値R,S、公開鍵nGが与えられた場合、hG/S + R(nG)/S = qG の関係が成り立つことを確かめることで、署名が正しいことを検証できる。
* h,G,R,S,nGのいずれからも秘密鍵nを知ることは困難である

という性質が成立するようになり、デジタル署名として必要な性質がそろっていることが分かります。

楕円曲線を利用したデジタル署名手順（まとめ）

おわりに

群は割といろんなアルゴリズムの話で出てくるので結び付けて覚えた方がいいんだろうなぁと思いました。
色々ガバガバなはずなので、ちゃんとした書籍なども当たることをお勧めいたします。