【第6回】いまさら聞けないメカ設計 暗算でできる強度設計
概要
メカ設計でよくあるのが強度不足です。
個人開発においては特に3Dプリンタ部品は一度試作してしまってから修正すると効率的です。
材料力学の基礎知識を用いて、細かい強度計算をすっ飛ばして暗算できる方法を紹介します。
対象読者
・3Dプリンタなどプロトタイピングをしている
・強度不足のときにどれくらい強度を増せばいいのかいつも適当になる
・材料力学を学んだことがない
結論
1.材料を分厚くした分の3乗だけ強くなる
2.部分的ならその割合だけ強くなる
3.幅を2倍にしたら2倍強くなる
たったこれだけです。
実証シミュレーション
幅10 mm, 厚さ1 mm, 長さ50 mmのABS(3Dプリンタでよく使うプラスチック材料)平板を基準として上記3つの強度UPをしたらどうなるかシミュレーションで確認します。
板の端を固定し、10 N(約1 kg)の荷重をかけたときのたわみ量をシミュレーションします。
基準サイズでは変形量が207.2 mmになりました。

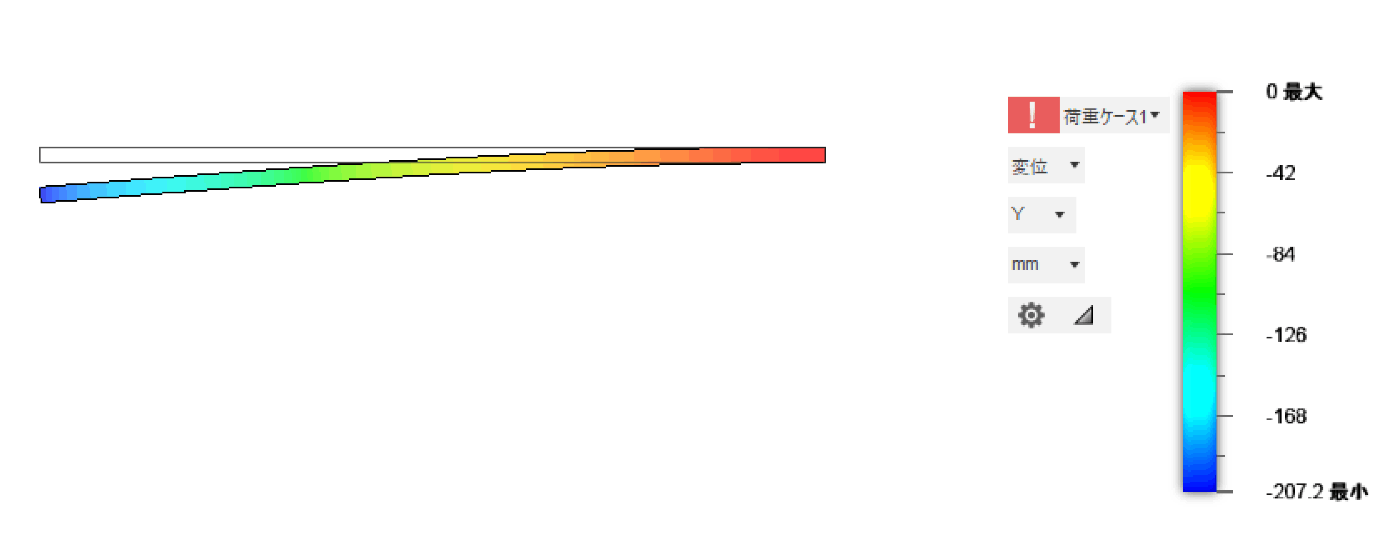
シミュレーションでは見た目が調整されていますが、実寸の変形量はこんな感じです。
※実際は破断します。
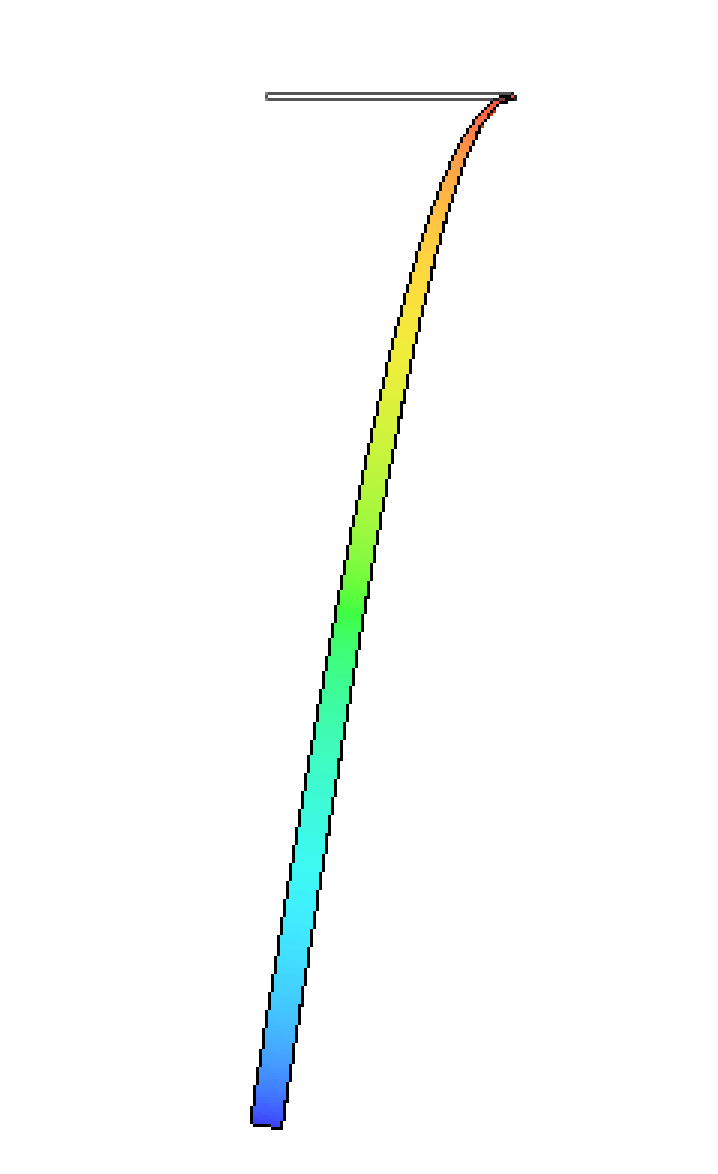
1.分厚くした場合
基準に対して厚さを2倍にすると26.44 mmたわみました。
2倍分厚くしたので2^3 = 8倍強くなり、変形量は約1/8になりました。
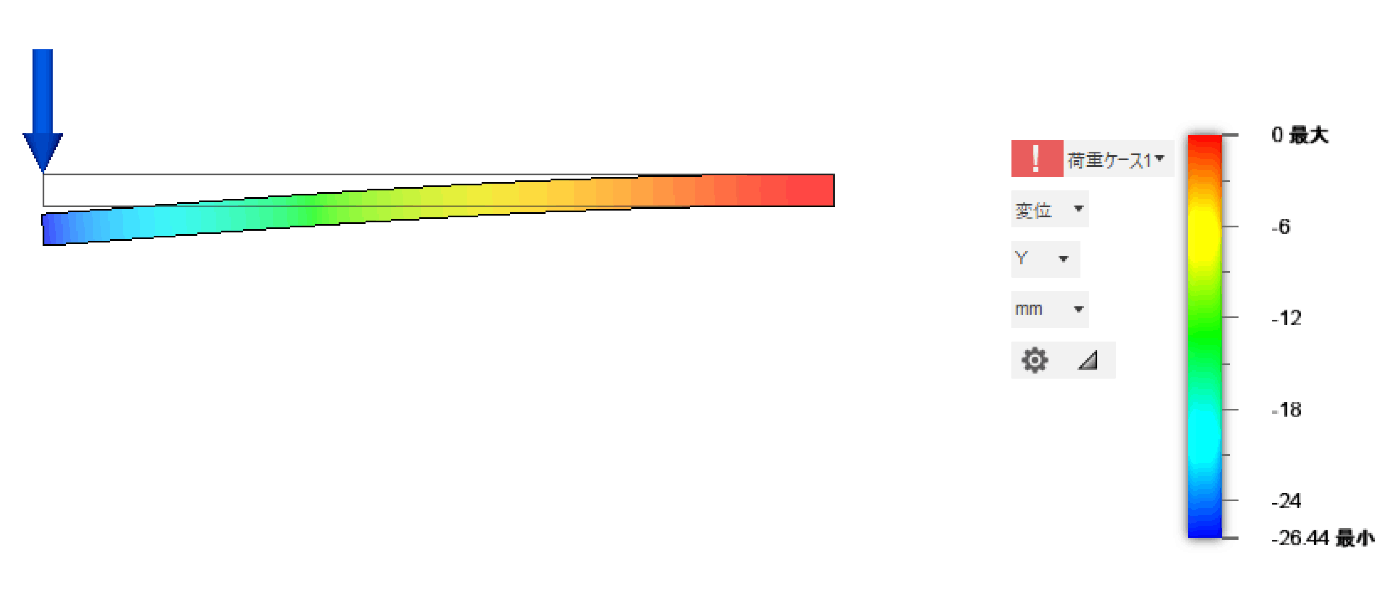
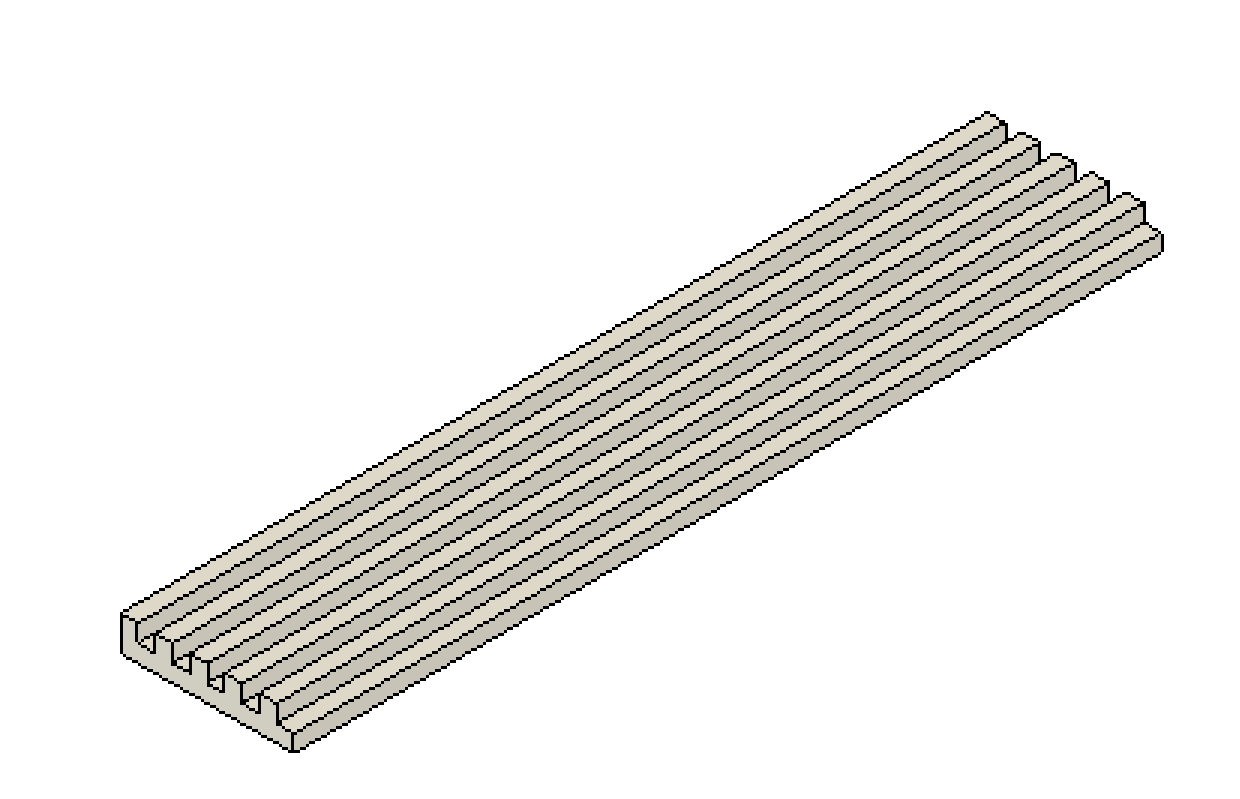
2.部分的に分厚く(しましまにまびく)した場合
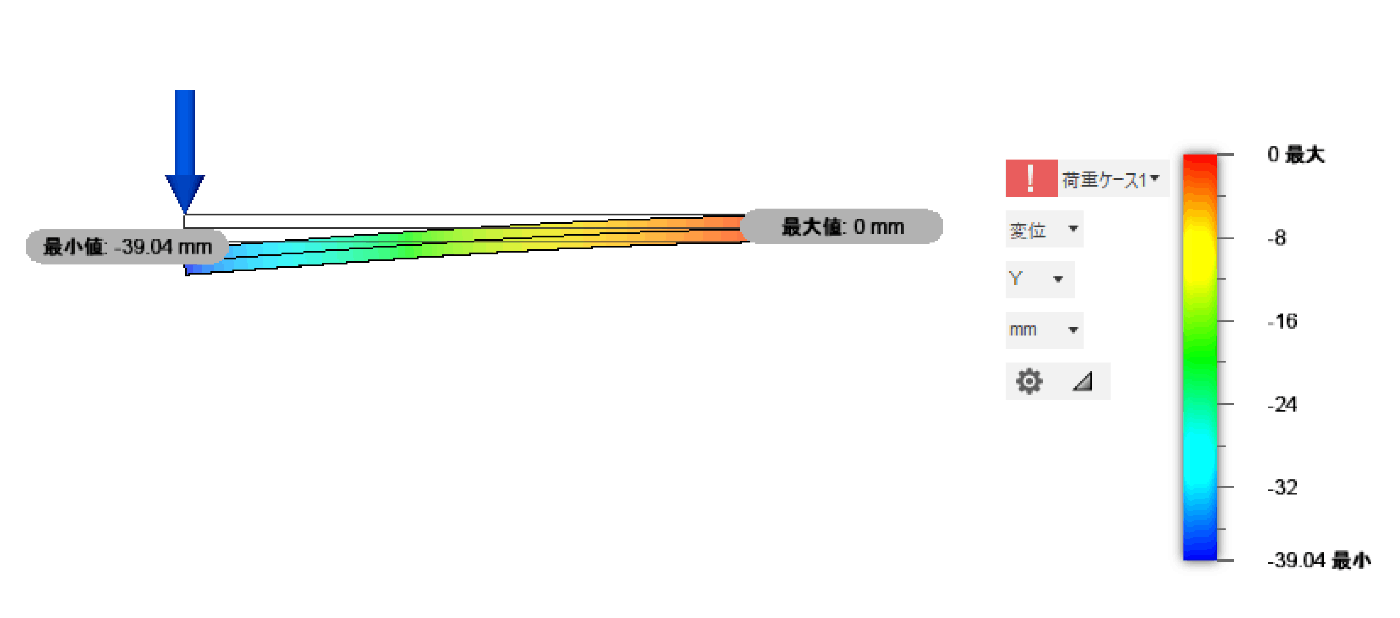
基準に対して半分の面積だけ厚さを2倍にすると 39.04 mmたわみました。
半分の面積だけ2倍分厚くしたので2^3/2 = 4倍強くなったのですが、変形量は約1/5になりました。
ちょっと強いですね。
形状が複雑な分、誤差が大きくなりました。
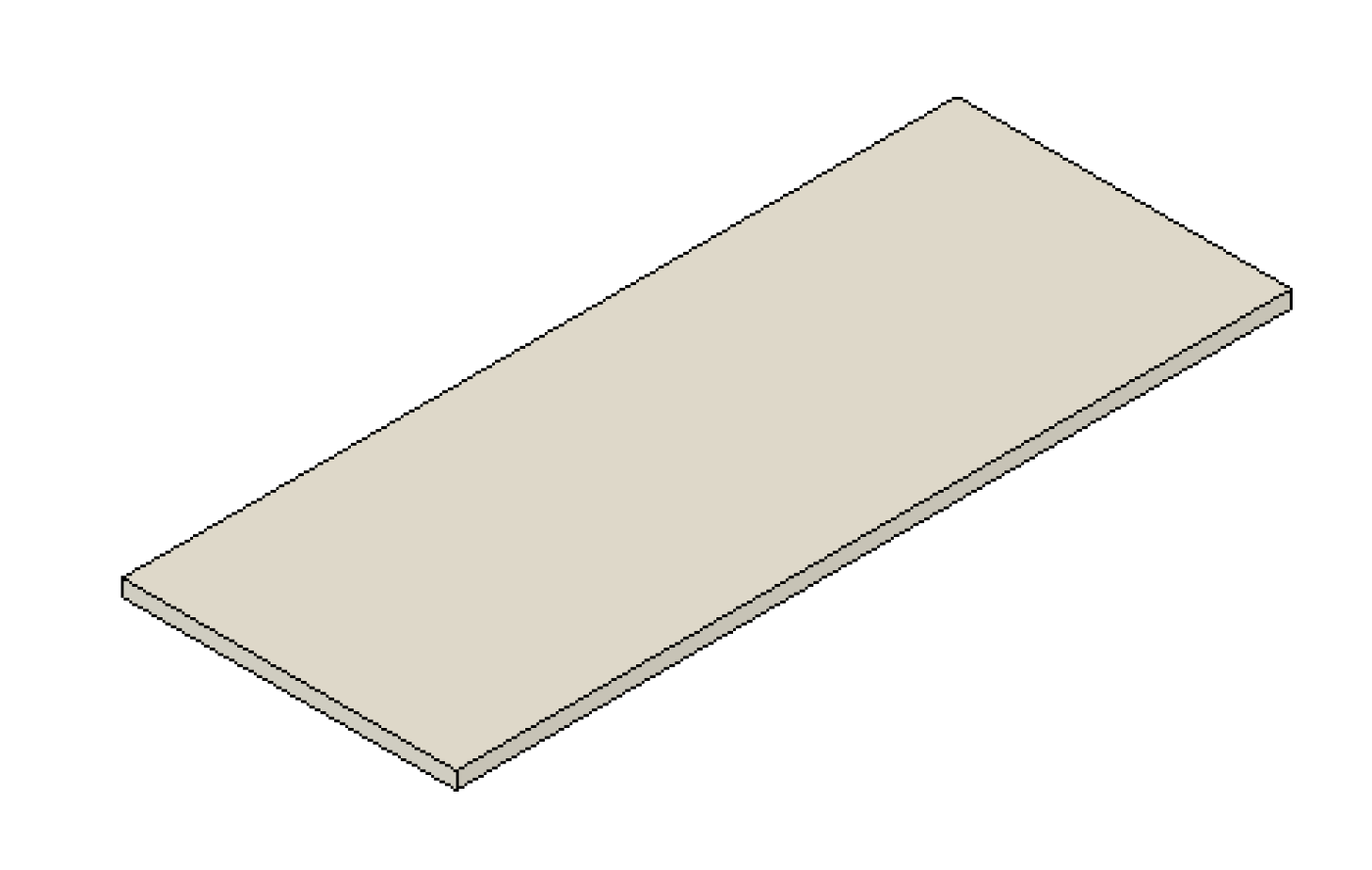
3.幅を広くした場合
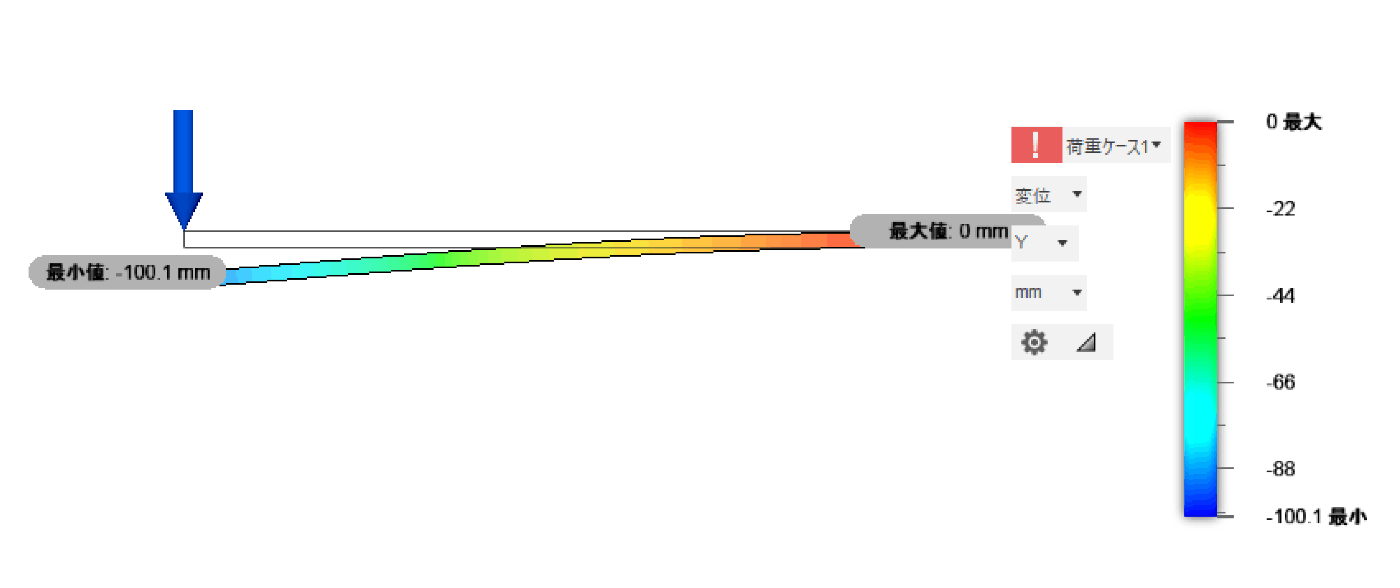
基準に対して幅を2倍にすると100.1 mmたわみました。
2倍広くして2倍強くなったので変形量は約1/2になりました。
まとめ
1.材料を分厚くした分の3乗だけ強くなる
2.部分的ならその割合だけ強くなる
3.幅を2倍にしたら2倍強くなる
という事実が伝わったかと思います。
2.3.はとても直感的ですが、1.の3乗というのをぜひ覚えてみてください。
幅を2倍にすると強度2倍ですが、厚さを2倍にすると強度8倍で効率が良いですね。
この知識の使い方ですが、
試作品に実際にかけたい荷重をかけてみて曲がり量をみます。
その曲がり量を何分の一にしたいかで厚さや幅をコントロールすると良いです。
Discussion