📨
SQLだけでナイーブベイズ分類モデルを実装する ― スパムメール分類を例に

畳屋民也
2025/12/13に公開
SQL でデータ分析をしていると、

機械学習や統計モデルを作りたいけど R や Python 立ち上げるのは面倒臭い！

ってことがよくあると思います。
そんな時は、そのまま SQL でモデル実装してしまえばいいのです！

（※そこまで複雑でないアルゴリズムに限る）
ということで、この記事ではスパムメール（迷惑メール）検知などでよく使われるナイーブベイズ分類モデルを SQL だけで実装する方法を紹介します。

 ナイーブベイズとは？まずはナイーブベイズがどのようなものかを解説します。
ナイーブベイズというとなんか難しそうに聞こえるかもしれませんが、基本的な原理は実はとてもシンプルです。
以下、代表的な応用例であるスパムメール検知を例に説明しようと思います。
ざっくりいうと、過去に届いたメールからラベルごとに各単語の出やすさを学習し、新しいメールがスパムメールに出やすい単語をどれだけ含んでいるかを見て、それをもとにそのメールがスパムかを判断する、ということを行います。


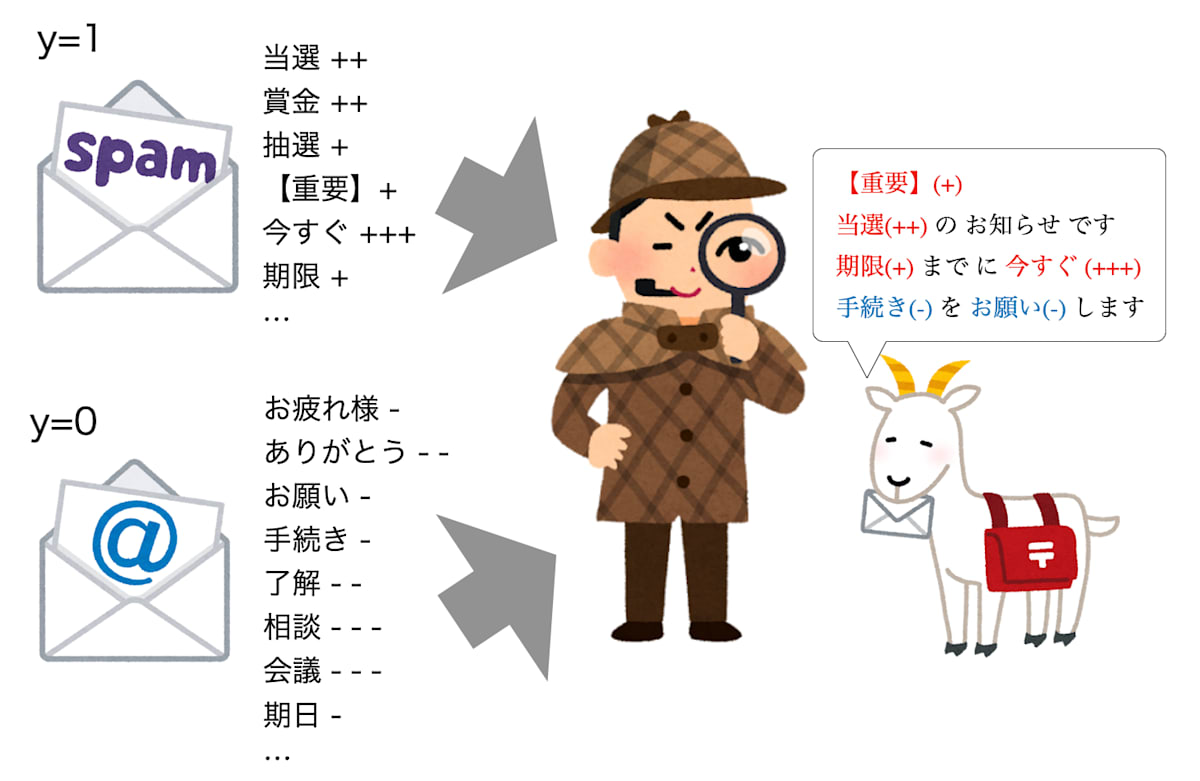
図: 過去のスパム／非スパムメールから単語の出現傾向を学習し、新しいメールを判定するナイーブベイズの模式図
まずは過去に届いたスパムかそうでないかがわかっているメールに着目し、文面に含まれるそれぞれの単語がスパムメールの中にどれだけの割合で含まれていたか、スパム以外のメールの中にどれだけの割合で含まれていたかを数えます。
そうすると、単語によって非スパムよりスパムメールの方でより現れやすい・現れにくいといった違いが見えてくるはずです。
ここで、手元に届いたメールの文面にスパムメールに現れやすい単語が多く含まれていればそれだけスパム確率が高いだろうと考えます。
この考え方をもとに文面に含まれる単語を一つ一つ見ていき、スパムに現れやすい単語であれば大きな値を、スパム以外のメールに現れやすい単語であれば小さな値を取るように予測値を計算します。
こうして最終的に得られた予測値の大きさをもとに、届いたメールがスパムかどうかを判定します。
これがナイーブベイズによるスパムメール検知のざっくりとした考え方です。
実際の計算ではスパム/非スパムごとの各単語の出現率とメール全体におけるスパム/非スパムの割合を用いて、予測値として推定スパム確率を出力します。

 理論ここでは、ナイーブベイズの理論的側面について解説します。
実際に実装を行ううえで集計が必要になるパラメータが何かを数式を追いながら一つ一つ見ていきますが、数式全くワカラン！という方は「SQLによる実装」まで飛ばしてしまっても一応大丈夫です。

 問題設定引き続きスパムメール検知を題材に議論します。
メール文面を単語 s_i が並んだものとして \boldsymbol{d} = (s_1, s_2, ..., s_n) と表すことにします。

n はそのメールに含まれる合計単語数です。
そして、そのメールがスパムなら y=1、スパムでないなら y=0 となるような目的変数を y とします。
このとき、与えられたメール文面 \boldsymbol{d} に対してそれがスパムである確率は条件付き確率を用いて P(y=1 \vert \boldsymbol{d}) と表すことができます。
このスパム確率 P(y=1 \vert \boldsymbol{d}) はどのように求めればよいかを考えます。

 ベースとなる考え方まず、以下のような式変形を行います：

\begin{aligned}
P(y=1\vert \boldsymbol{d}) &= \frac{P(y=1, \boldsymbol{d})}{P(\boldsymbol{d})}\\
&= \frac{P(\boldsymbol{d} \vert y=1)P(y=1)}{P(\boldsymbol{d})}.
\end{aligned}
いわゆる「ベイズの定理」と呼ばれているものです。
これにより、メール全体におけるスパムメールの出現確率 P(y=1)、スパムメールの中で文面が \boldsymbol{d} で表せる確率 P(\boldsymbol{d}\vert y=1)、メール全体の中で文面が \boldsymbol{d} であるものが現れる確率 P(\boldsymbol{d}) をそれぞれ求めればいいことがわかります。
なお、P(\boldsymbol{d}) は以下のようにして y と \boldsymbol{d} の同時分布 P(y, \boldsymbol{d}) = P(\boldsymbol{d}\vert y)P(y) を周辺化して求めることができます：

\begin{aligned}
P(\boldsymbol{d}) &= P(y=0, \boldsymbol{d}) + P(y=1, \boldsymbol{d})\\
&= P(\boldsymbol{d}\vert y=0)P(y=0) + P(\boldsymbol{d}\vert y=1)P(y=1)
\end{aligned}

 「ナイーブ」な独立性の過程では、条件付き確率 P(\boldsymbol{d}\vert y=1), \, P(\boldsymbol{d}\vert y=0) はどのように求めればいいでしょうか？
ここで、以下のような仮定をおきます：

P(\boldsymbol{d}\vert y) = \prod_{i=1}^n P(s_i \vert y).
この仮定の意味するところをスパムメール (y=1) の場合の P(\boldsymbol{d}\vert y=1) で説明すると、「スパムメールに含まれる単語は、互いに独立な分布から生成される」というものです（非スパムメールでも同様だが、スパムメールとは分布が異なっていてよい）。
実際にはひとつひとつのメールによって出やすい単語・出にくい単語が違いますし、単語同士の相関（続けて出やすい・出にくいなど）もあるのでこれは強い仮定です。
上記の仮定を用いると、P(y=1 \vert \boldsymbol{d}) は以下のように表すことができます：

P(y=1\vert \boldsymbol{d})
= \frac{\left\{\prod_{i=1}^n P(s_i \vert y=1)\right\} P(y=1)}{P(\boldsymbol{d})}.

 Bag-of-Words による表現ところで、上記では s_i は「メール文面中に含まれる i 番目の単語」を意味していますが、集計上は「それぞれの単語がメール文面中に何回出たか？」という形でデータを保持することが多いです。
そこで、メールに含まれる重複を除いた K 種類の単語全体を \{w_k\}_{k=1}^K で表し、各単語がメール文面中に含まれた回数を \{n_k\}_{k=1}^K と表すことにします。

このような表し方を、自然言語処理では Bag-of-Words (BoW) 表現と言います。
この表現を用いると、P(s_i\vert y) の積は以下のように書き換えることができます：

\prod_{i=1}^n P(s_i\vert y) = \prod_{k=1}^K P(w_k\vert y)^{n_k}.
上記では、同じ単語 w_k は何度出てきてもその確率は P(w_k \vert y) で変わらないので、回数 n_k 回分まとめています。
これを用いると、再び P(y=1\vert \boldsymbol{d}) は以下のように書き換えられます：

P(y=1\vert \boldsymbol{d})
= \frac{\left\{\prod_{k=1}^K P(w_k \vert y=1)^{n_k}\right\} P(y=1)}{P(\boldsymbol{d})}. \tag{1}
なお、P(\boldsymbol{d}) についても以下のように表すことができます:

\begin{aligned}
    P(\boldsymbol{d})
    &= P(\boldsymbol{d}\vert y=0)P(y=0) + P(\boldsymbol{d}\vert y=1)P(y=1)\\
    &= \left\{\prod_{k=1}^K P(w_k \vert y=0)^{n_k}\right\} P(y=0)\\
    & \qquad + \left\{\prod_{k=1}^K P(w_k \vert y=1)^{n_k}\right\} P(y=1).
\end{aligned}

 実データでのモデル学習方法上記の式(1)に従って、文面が単語列 \boldsymbol{d}_0 で表される新しく届いたメールがスパムである確率 P(y=1 \vert \boldsymbol{d}_0) を予測します。
そのためには、モデルパラメータとして \{P(w_k\vert y=1), P(w_k\vert y=0)\}_{k=1}^K と P(y=1), P(y=0) を学習する必要があります。
データからこのモデルの学習を行う際は、過去に届いたメール文面 \boldsymbol{d}_i とスパム・非スパムラベル y_i がペアになったデータセット \{\boldsymbol{d}_i, y_i\}_{i=1}^D （D はデータセット数）を学習データとして用います。

 条件付き単語出現確率 P(w_k \vert y) の推定学習データ全体 \{\boldsymbol{d}_i\}_{i=1}^D に含まれる単語を \{w_k\}_{k=1}^K （K は全メールに含まれる単語のユニーク数）として、ラベル y で条件付けされた各単語の出現確率 P(w_k\vert y) を推定します。
P(w_k\vert y=1), P(w_k\vert y=0) は「スパム/非スパムメールの中で k 番目の単語 w_k が登場する確率」なので、以下がわかれば推定できます：

N_1, \, N_0: スパム（y=1）/ 非スパム（y=0）全体での全ワード登場回数の合計

N_{1,k}, \, N_{0,k}: スパム（y=1）/ 非スパム（y=0）全体における k 番目の単語 w_k の登場回数
単純に考えれば、N_{1,k} / N_1 が P(w_k\vert y=1) の推定値 \hat{P}(w_k\vert y=1) になります。同様にして、P(w_k\vert y=0) の推定値 \hat{P}(w_k\vert y=0) についても単純には N_{0,k} / N_0 で求められます（後述しますが、実際にはそれでは問題が生じるので補正を加えます）。

 各ラベルの出現確率 P(y) の推定P(y=1), \, P(y=0) については、「あるメールがスパム / 非スパムである確率」なので、その推定値はそれぞれスパム/非スパムの件数を全メール件数で割ることで求められます：

\hat{P}(y=1) = \frac{1}{D}\sum_{i=1}^D y_i, \quad \hat{P}(y=0) = \frac{1}{D}\sum_{i=1}^D (1 - y_i). \tag{2}

 実装上の補足以上から、あるメール文面 \boldsymbol{d}_0 が与えられたとき、全文面中に含まれる各単語の登場回数を \{n_{0,k}\}_{k=1}^{K'} と置くと、このメールがスパムである確率 P(y=1\vert \boldsymbol{d}_0) は以下のように推定できます：

\begin{aligned}
    \hat{P}(y=1 \vert \boldsymbol{d}_0)
    &= \frac{\left\{\prod_{k=1}^{K'} \hat{P}(w_k \vert y=1)^{n_{0,k}}\right\} \hat{P}(y=1)}{\hat{P}(\boldsymbol{d}_0)},\\
    \hat{P}(\boldsymbol{d}_0) &= \left\{\prod_{k=1}^{K'} \hat{P}(w_k \vert y=0)^{n_{0,k}}\right\} \hat{P}(y=0)\\
     &\qquad + \left\{\prod_{k=1}^{K'} \hat{P}(w_k \vert y=1)^{n_{0,k}}\right\} \hat{P}(y=1). \tag{3}
\end{aligned}
なお、K' は、予測データも含めたデータセット全体に登場する単語のユニーク数です。予測データに学習データには含まれていなかった新たな単語 \{w_l\}_{l=K+1}^{K'} が現れた場合を想定しています。
モデルパラメータ \hat{P}(w_k\vert y), \hat{P}(y) はいずれも単語の数やデータラベルの数をカウントすれば求められるので、SQL の SUM や GROUP BY を駆使して集計できそうです。
これに加えて、実際に上記の計算を行う際には、いくつか必要になる計算テクニックがあります。

 ゼロ頻度問題の回避前述のように \hat{P}(w_k \vert y) としてそのままスパム/非スパムメール文中の単語の登場頻度 N_{y,k} / N_y を用いた場合、困ったことが発生します。
学習データに含まれなかったものの予測対象メールには含まれている単語 w_l では、N_{y,l} = 0 となるため \hat{P}(w_l \vert y) = 0 になってしまうのです。
これにより、例えば学習データではスパムメールに "hoge" という単語が含まれていなかったら、予測対象メールの文中に "hoge" が登場した時点でそれがいくら明らかにスパムメールに見えようが予測確率は 0 になってしまいます。
学習データに登場していても、スパム/非スパムいずれか片方のラベルでしか現れなかった単語についても同様のことがいえます。
これを避けるために平滑化というものを行い、以下のように単語出現確率を補正します：

\hat{P}(w_k \vert y) = \frac{N_{y,k} + \alpha}{N_y + K\alpha} \tag{4}
K: 学習データ全体に登場する単語のユニーク数

\alpha: 平滑化パラメータ（ハイパーパラメータ）
こうすることで、学習データに登場しなかった単語 w_l でも \hat{P}(w_l \vert y) = \alpha / (N_y + K\alpha) のように0にならずに済みます。
なお、\alpha は厳密には交差検証などをして決定する必要がありますが、ここでは簡単のため \alpha=1 とおいてしまいます。[1]

 数値のアンダーフロー回避実際に計算してみるとわかるのですが、確率の積の部分 \prod_{k=1}^{K'} \hat{P}(w_k\vert y)^{n_k} をそのまま計算すると値が極端に小さくなり、特にメールの語数が多い場合ほとんど0になってしまいます。
そのため、次のように対数を取って和の形に変換します:

\prod_{k=1}^{K'} \hat{P}(w_k\vert y)^{n_k} = \exp \left\{ \sum_{k=1}^{K'} n_k \log \hat{P}(w_k\vert y)\right\}
なお、SQL では複数行にわたる値の積を求めることができないのですが、上記の方法をとることで SUM 関数で集計できるようになるという利点もあります。
この考え方を用いて、文面 \boldsymbol{d}_0 からなる予測対象メールについてスパム確率を予測する際は、式(3)を以下のように変換して計算を行います：

\begin{aligned}
    \hat{P}(y=1 \vert \boldsymbol{d}_0)
    &= \frac{1}{1 + \frac{\hat{P}(y=0)}{\hat{P}(y=1)}\prod_{k=1}^{K'}\frac{\hat{P}(w_k \vert y=0)^{n_{0,k}}}{\hat{P}(w_k \vert y=1)^{n_{0,k}}}}\\
    &= \frac{1}{1 + \frac{\hat{P}(y=0)}{\hat{P}(y=1)}\exp \left\{\sum_{k=1}^{K'} n_{0,k} \log\frac{\hat{P}(w_k \vert y=0)}{\hat{P}(w_k \vert y=1)}\right\}}\\
    &= \frac{1}{1 + \frac{\hat{P}(y=0)}{\hat{P}(y=1)}\exp \left\{-\sum_{k=1}^{K'} n_{0,k} \log\frac{\hat{P}(w_k \vert y=1)}{\hat{P}(w_k \vert y=0)}\right\}}. \tag{5}
\end{aligned}
なお、上記の指数関数部分の中に出てきた

\log\frac{\hat{P}(w_k \vert y=1)}{\hat{P}(w_k \vert y=0)} = \log\hat{P}(w_k \vert y=1) - \log \hat{P}(w_k \vert y=0)
という量は、対数尤度比 (log-likelihood ratio) と呼ばれるものです。
後ほどまた触れますが、この量は単語 w_k が 通常のメールと比べてスパムメールの方が登場しやすい単語であるほど正の方向に大きな値をとり、逆にスパムメールの方が出にくい単語であるほど負の方向に大きな値をとります。

 SQL による実装やや込み入った話が続きましたが、これまでの議論をまとめると、以下を集計すればナイーブベイズ分類モデルを作成し、推定スパム率 \hat{P}(y=1\vert \boldsymbol{d}_0) を得ることができます：


求めたいもの
必要な集計値
集計値の説明


式(4) スパム/非スパムメールにおける各単語の推定登場確率 \hat{P}(w_k \vert y) = \frac{N_{y,k} + \alpha}{N_y + K\alpha}

\left\{ N_{1,k}, N_{0,k}\right\}_{k=1}^K
スパム/非スパムメール中の各単語 w_k の登場回数


N_1, \, N_0
スパム/非スパムメールに含まれる単語総数


K
学習データ全体に含まれる単語のユニーク数

式(2) スパム/非スパムメールの推定割合 \hat{P}(y=1) = \frac{1}{D}\sum_{i=1}^D y_i, \quad \hat{P}(y=0) = \frac{1}{D}\sum_{i=1}^D (1 - y_i)

D
学習データ数


\sum_{i=1}^D y_i, \, \sum_{i=1}^D (1-y_i)
学習データ中のスパムメール数・非スパムメール数

式(5) 推定スパム率
 \hat{P}(y=1\vert \boldsymbol{d_0})=\frac{1}{1 + \frac{\hat{P}(y=0)}{\hat{P}(y=1)}\exp \left\{-\sum_{k=1}^{K'} n_{0,k} \log\frac{\hat{P}(w_k \vert y=1)}{\hat{P}(w_k \vert y=0)}\right\}}

\{n_{0,k}\}_{k=1}^{K'}
予測対象メールの文中に含まれる各単語 \{w_k\}_{k=1}^{K'} の登場回数

これなら SQL でも実装できますね！

ということで、実際にやってみましょう！

 使用データセットkaggle で公開されている以下のデータセットを用います。

https://www.kaggle.com/datasets/uciml/sms-spam-collection-dataset
これは、SMS のメッセージに SPAM（迷惑メール） / HAM（非スパム）のラベルが付与されたものです。



データ型
内容
例


カラム1
STRING
正解ラベル
(spam ... 13%, ham ... 87%)
spam

カラム2
STRING
メッセージ文面 (5169種類)
This is the 2nd time we have tried 2 contact u...

こちらをサイトからダウンロードしたうえで、いったん文字コードをUTF-8に変換した上で BigQuery に取り込みました。

 0. データ読み込み + 前処理まず BigQuery 上でデータを読み込みますが、このままでは扱いづらいので以下の処理を行いました：
重複メッセージの削除
正解ラベルを spam or ham の文字列から 1 or 0 に変換
メッセージごとにIDの作成 (message_id)
学習データ・テストデータへの分割
再現性のため message_id をもとに擬似ランダムな数値を発生させ、その値をもとにメッセージ全体の20%をテストデータに振り分けました。

-- ==========================================
-- パラメータ
-- ==========================================
DECLARE TEST_SPLIT_RATIO INT64 DEFAULT 20;  -- 20% を test データにする
DECLARE ALPHA FLOAT64 DEFAULT 1.0;  -- 平滑化 (smoothing) パラメータ

WITH
  -- ==========================================
  -- 0. データの読み込みと前処理
  -- ==========================================
  import_sms_dataset AS (
    -- BQ に取り込んだ SMS Spam Collection Dataset を読み込む
    -- https://www.kaggle.com/code/pavelbogdanov/spam-filtering-with-naive-bayes
    SELECT
      string_field_0 AS spam_or_ham,
      string_field_1 AS message
    FROM `<project_id>.naive_bayes.sms_spam_collection`
  ),
  preprocessed_sms_dataset AS (
    -- SMS Spam Collection Dataset の前処理を行う
    WITH
      remove_duplicated_messages AS (
        -- 同一の message 文面があればまとめる
        SELECT
          message,
          MAX(IF(spam_or_ham = "spam", 1, 0)) AS is_spam,
        FROM
          import_sms_dataset
        GROUP BY message
      ),
      assign_id AS (
        -- オリジナルのデータにIDがなかったため、便宜的に付与する
        SELECT
          ROW_NUMBER() OVER () AS message_id,
          is_spam,
          message,
        FROM remove_duplicated_messages
      )
    -- 学習データ・テストデータに一定割合で分ける
    SELECT
      *,
      IF(
        MOD(ABS(FARM_FINGERPRINT(CAST(message_id AS STRING))), 100)
          >= 100 - TEST_SPLIT_RATIO,
        1,
        0)
        AS is_test
    FROM assign_id
  ),
この処理により、以下のような形のデータになります（メッセージ本文は適当に置き換えています）：


message_id
is_spam
message
is_test


1
0
Hoge fuga piyo fuga.
0

2
0
Piyo piyo hoge HOO :)
0

3
0
HOGE inc. meeting at 10.
1

4
1
WIN!!! CLICK HOO TO CLAIM NOW!
0

5
1
Click PIYO to win PiYo!!!
1


 1. メッセージごとに各単語の登場回数を集計次に、文面を単語に分割し、メッセージごとに単語の登場回数を集計します。
その際、大文字は小文字に揃え、句読点(.,)や!?の記号は除去します。

これにより、文頭・文末や強調表現関係なく同じ単語をひとまとめにして扱います。
  -- ==========================================
  -- 1. メッセージごとに各単語の登場回数を集計
  -- ==========================================
  count_words AS (
    WITH
      split_into_words AS (
        -- スペースで区切った文字列を単語とみなす
        SELECT
          *
        FROM
          preprocessed_sms_dataset, UNNEST(SPLIT(message, " ")) AS splitted_word
      ),
      clean_words AS (
        -- ".,?!"は除外したうえで、小文字に揃える
        SELECT
          *,
          LOWER(REGEXP_REPLACE(splitted_word, r"[.,?!]", "")) AS word
        FROM split_into_words
      )
    -- 単語の登場回数を集計する
    SELECT
      message_id,
      is_test,
      is_spam,
      word,
      COUNT(*) AS cnt
    FROM
      clean_words
    GROUP BY
      message_id, is_test, is_spam, word
  ),

こうすることで、以下のようなデータが出来上がります：


message_id
is_test
is_spam
word
cnt


1
0
0
hoge
1

1
0
0
fuga
2

1
0
0
piyo
1

2
0
0
hoge
1

2
0
0
piyo
2

2
0
0
hoo
1

2
0
0
:)
1

3
1
0
hoge
1

3
1
0
inc
1

3
1
0
meeting
1

3
1
0
at
1

3
1
0
10
1

4
0
1
win
1

4
0
1
click
1

4
0
1
hoo
1

4
0
1
to
1

4
0
1
claim
1

4
0
1
now
1

5
1
1
click
1

5
1
1
piyo
2

5
1
1
to
1

5
1
1
win
1


 2. モデルパラメータの学習次に、学習データに絞ってモデルパラメータの学習を行います。
  -- ==========================================
  -- 2. モデルパラメータの学習
  --  * クラス別単語確率 log P(w | y) を求める
  --  * 非スパム/スパムの登場確率 P(y) を求める
  -- ==========================================
  train_data AS (
    SELECT
      *
    FROM count_words
    WHERE is_test = 0
  ),


message_id
is_test
is_spam
word
cnt


1
0
0
hoge
1

1
0
0
fuga
2

1
0
0
piyo
1

2
0
0
hoge
1

2
0
0
piyo
2

2
0
0
hoo
1

2
0
0
:)
1

4
0
1
win
1

4
0
1
click
1

4
0
1
hoo
1

4
0
1
to
1

4
0
1
claim
1

4
0
1
now
1

まずは各単語の推定登場確率 \hat{P}(w_k \vert y) = \frac{N_{y,k} + \alpha}{N_y + K\alpha} を求めるために、\{N_{0,k}, N_{1,k}\}_{k=1}^K, N_0, N_1, K を計算します。
  -- 2-1. クラス別単語頻度を集計 → log P(w | y) を求める
  count_by_word_train AS (
    -- 非スパム/スパム別に単語ごとの登場回数 N_{0,k}, N_{1,k} を計算する
    SELECT
      word,
      SUM(IF(is_spam = 0, cnt, 0)) AS cnt_in_y0,  -- N_{0,k}
      SUM(IF(is_spam = 1, cnt, 0)) AS cnt_in_y1,  -- N_{1,k}
    FROM train_data
    GROUP BY word
  ),
  count_total_words_train AS (
    -- 非スパム/スパム全体の合計単語数 N_0, N_1 と、学習データに登場する単語のユニーク数 K を計算する
    SELECT
      SUM(cnt_in_y0) AS total_cnt_in_y0,  -- N_0
      SUM(cnt_in_y1) AS total_cnt_in_y1,  -- N_1
      COUNT(*) AS count_unique_words  -- K
    FROM
      count_by_word_train
  ),
先ほどのサンプルデータでいうと以下のようになります：
count_by_word_train \{N_{0,k}, N_{1,k}\}_{k=1}^K


word
cnt_in_y0
cnt_in_y1


:)
1
0

claim
0
1

click
0
1

fuga
2
0

hoge
2
0

hoo
1
1

now
0
1

piyo
3
0

to
0
1

win
0
1

count_total_words_train N_0, N_1, K


total_cnt_in_y0
total_cnt_in_y1
count_unique_words


9
6
10

次に、\hat{P}(w_k \vert y) を計算しますが、後続の処理のために対数にしておきます：

\log \hat{P}(w_k \vert y) = \log \left(N_{y,k} + \alpha\right) - \log \left(N_y + K\alpha \right)
なお、ハイパーパラメータ \alpha は、冒頭で定義しておいたクエリ変数 ALPHA を用います。
  calc_logprob_of_words AS (
    -- 単語ごとに条件付き登場確率を計算し対数をとる log P(w | y)
    SELECT
      *,
      LOG(cnt_in_y0 + ALPHA) - LOG(total_cnt_in_y0 + count_unique_words * ALPHA)
        AS logprob_word_in_y0,  -- log P(w | y=0)
      LOG(cnt_in_y1 + ALPHA) - LOG(total_cnt_in_y1 + count_unique_words * ALPHA)
        AS logprob_word_in_y1,  -- log P(w | y=1)
    FROM count_by_word_train, count_total_words_train
  ),


word
log_prob_word_in_y0
log_prob_word_in_y1


:)
-2.25129
-2.77259

claim
-2.94444
-2.07944

click
-2.94444
-2.07944

fuga
-1.84583
-2.77259

hoge
-1.84583
-2.77259

hoo
-2.25129
-2.07944

now
-2.94444
-2.07944

piyo
-1.55814
-2.77259

to
-2.94444
-2.07944

win
-2.94444
-2.07944

なお、学習データに含まれない単語 w_l がテストデータに出た場合は \hat{P}(w_l \vert y) = \frac{\alpha}{N_y + K\alpha} になるように、あらかじめ計算しておきます：
  calc_log_prob_for_smoothing AS (
    -- 学習データに登場しなかった単語については、P(w | y) を alpha / (N_y + K alpha) で代用する
    SELECT
      LOG(ALPHA) - LOG(total_cnt_in_y0 + count_unique_words * ALPHA)
        AS logprob_for_smoothing_in_y0,
      LOG(ALPHA) - LOG(total_cnt_in_y1 + count_unique_words * ALPHA)
        AS logprob_for_smoothing_in_y1,
    FROM
      count_total_words_train
  ),


log_prob_word_in_y0
log_prob_word_in_y1


-2.94444
-2.77259

最後に学習データ内のスパム/非スパムメッセージの割合 \hat{P}(y=1) = \frac{1}{D}\sum_{i=1}^D y_i, \quad \hat{P}(y=0) = \frac{1}{D}\sum_{i=1}^D (1 - y_i) も計算します。

ここでは単語数ではなくメッセージ数単位で集計することに気をつけてください。
  -- 2-1. 各クラスの登場頻度から、非スパム/スパムの登場確率 P(y) を求める
  calc_spam_prob_train AS (
    SELECT
      COUNT(DISTINCT IF(is_spam = 0, message_id, NULL))
        / COUNT(DISTINCT message_id) AS p_y0,
      COUNT(DISTINCT IF(is_spam = 1, message_id, NULL))
        / COUNT(DISTINCT message_id) AS p_y1,
    FROM
      train_data
  ),


p_y0
p_y1


0.666667
0.333333


 3. テストデータに対して推論計算モデルパラメータの推定ができたので、今度はテストデータに作成したモデルを当てて推論を行なっていきます。
  -- ==========================================
  -- 3. テストデータに対して推論計算
  -- ==========================================
  test_data AS (
    SELECT
      *
    FROM
      count_words
    WHERE is_test = 1
  ),


message_id
is_test
is_spam
word
cnt


3
1
0
hoge
1

3
1
0
inc
1

3
1
0
meeting
1

3
1
0
at
1

3
1
0
10
1

5
1
1
click
1

5
1
1
piyo
2

5
1
1
to
1

5
1
1
win
1

まずは、テストデータとしたメッセージに含まれる単語一つ一つに先ほど計算した \log \hat{P}(w_k \vert y) を紐づけていきます。

テストデータで初めて登場する単語については、\log \frac{\alpha}{N_y + K\alpha} となるように calc_logprob_for_smoothing で計算した値をとってきます。
  join_model_params_to_test_data AS (
    -- 各テストデータに含まれる単語に、学習データで計算した log P(w | y) を紐づける
    -- テストデータで新たに登場した単語については、平滑化により求めた値で置き換える（ゼロ頻度問題の回避）
    SELECT
      message_id,
      word,
      cnt,  -- n_k
      COALESCE(logprob_word_in_y0, logprob_for_smoothing_in_y0)
        AS logprob_word_in_y0,  -- log P(w_k | y=0)
      COALESCE(logprob_word_in_y1, logprob_for_smoothing_in_y1)
        AS logprob_word_in_y1,  -- log P(w_k | y=1)
    FROM test_data
    LEFT JOIN
      calc_logprob_of_words
      USING (word)
    CROSS JOIN calc_log_prob_for_smoothing
  ),


message_id
word
cnt
log_prob_word_in_y0
log_prob_word_in_y1


3
hoge
1
-1.84583
-2.77259

3
inc
1
-2.94444
-2.77259

3
meeting
1
-2.94444
-2.77259

3
at
1
-2.94444
-2.77259

3
10
1
-2.94444
-2.77259

5
click
1
-2.94444
-2.07944

5
piyo
2
-1.55814
-2.77259

5
to
1
-2.94444
-2.07944

5
win
1
-2.94444
-2.07944

そのうえで、メッセージごとに以下の量を計算します：

\begin{aligned}
 {\rm LLR}(\boldsymbol{d}_0\vert y) &= \sum_{k=1}^{K'} n_{0,k} \log\frac{\hat{P}(w_k \vert y=1)}{\hat{P}(w_k \vert y=0)}\\
  &= \sum_{k=1}^{K'} n_{0,k} \left\{\log\hat{P}(w_k \vert y=1) - \log \hat{P}(w_k \vert y=0)\right\}
\end{aligned}
これは、理論パートで触れた対数尤度比 (log-likelihood ratio) の総和を意味します。
これを用いて、予測スパム確率を以下のように求めることができます：

\begin{aligned}
\hat{P}(y=1\vert \boldsymbol{d_0}) &=\frac{1}{1 + \frac{\hat{P}(y=0)}{\hat{P}(y=1)}\exp \left\{-\sum_{k=1}^{K'} n_{0,k} \log\frac{\hat{P}(w_k \vert y=1)}{\hat{P}(w_k \vert y=0)}\right\}}\\
&= \frac{1}{1 + \frac{\hat{P}(y=0)}{\hat{P}(y=1)}\exp \left\{-{\rm LLR}(\boldsymbol{d}_0\vert y)\right\}}.
\end{aligned}
  calc_llr_sum_for_each_message AS (
    -- メッセージごとに、対数尤度比log P(w_k | y=1) - log P(w_k | y=0) の合計を計算する
    SELECT
      message_id,
      SUM(cnt * (logprob_word_in_y1 - logprob_word_in_y0))
        AS llr_sum  -- Σ_k n_k {log P(w_k | y=1) - Σ log P(w_k | y=0)}
    FROM
      join_model_params_to_test_data
    GROUP BY message_id
  ),
  calc_spam_prob_test AS (
    -- スパム予測確率 P(y=1 | d) を計算する
    SELECT
      *,
      SAFE_DIVIDE(1, 1 + EXP(-llr_sum) * p_y0 / p_y1)
        AS spam_prob  -- P(y=1 | d)
    FROM calc_llr_sum_for_each_message
    CROSS JOIN calc_spam_prob_train
  )


message_id
llr_sum
p_y0
p_y1
spam_prob


3
-0.239361
0.666667
0.333333
0.282416

5
0.166104
0.666667
0.333333
0.371207


 4. 予測結果と元データを紐づける以上でテストデータでの推論が完了しました！
最後に分析しやすいように、正解ラベルと元のメッセージを紐づけましょう。
-- ==========================================
-- 4. 予測結果と元データを紐づける
-- ==========================================
SELECT
  message_id,
  spam_prob,
  is_spam,
  message
FROM calc_spam_prob_test
JOIN preprocessed_sms_dataset
  USING (message_id)
ORDER BY message_id


message_id
spam_prob
is_spam
message


3
0.282416
0
HOGE inc. meeting at 10.

5
0.371207
1
Click PIYO to win PiYo!!!


 クエリ全貌クエリ全体を通して掲載すると以下のようになります：
詳細-- ==========================================
-- パラメータ
-- ==========================================
DECLARE TEST_SPLIT_RATIO INT64 DEFAULT 20;  -- 20% を test データにする
DECLARE ALPHA FLOAT64 DEFAULT 1.0;  -- 平滑化 (smoothing) パラメータ

WITH
  -- ==========================================
  -- 0. データの読み込みと前処理
  -- ==========================================
  import_sms_dataset AS (
    -- BQ に取り込んだ SMS Spam Collection Dataset を読み込む
    -- https://www.kaggle.com/code/pavelbogdanov/spam-filtering-with-naive-bayes
    SELECT
      string_field_0 AS spam_or_ham,
      string_field_1 AS message
    FROM `<project_id>.naive_bayes.sms_spam_collection`
  ),
  preprocessed_sms_dataset AS (
    -- SMS Spam Collection Dataset の前処理を行う
    WITH
      remove_duplicated_messages AS (
        -- 同一の message 文面があればまとめる
        SELECT
          message,
          MAX(IF(spam_or_ham = "spam", 1, 0)) AS is_spam,
        FROM
          import_sms_dataset
        GROUP BY message
      ),
      assign_id AS (
        -- オリジナルのデータにIDがなかったため、便宜的に付与する
        SELECT
          ROW_NUMBER() OVER () AS message_id,
          is_spam,
          message,
        FROM remove_duplicated_messages
      )
    -- 学習データ・テストデータに一定割合で分ける
    SELECT
      *,
      IF(
        MOD(ABS(FARM_FINGERPRINT(CAST(message_id AS STRING))), 100)
          >= 100 - TEST_SPLIT_RATIO,
        1,
        0)
        AS is_test
    FROM assign_id
  ),

  -- ==========================================
  -- 1. メッセージごとに各単語の登場回数を集計
  -- ==========================================
  count_words AS (
    WITH
      split_into_words AS (
        -- スペースで区切った文字列を単語とみなす
        SELECT
          *
        FROM
          preprocessed_sms_dataset, UNNEST(SPLIT(message, " ")) AS splitted_word
      ),
      clean_words AS (
        -- ".,?!"は除外したうえで、小文字に揃える
        SELECT
          *,
          LOWER(REGEXP_REPLACE(splitted_word, r"[.,?!]", "")) AS word
        FROM split_into_words
      )
    -- 単語の登場回数を集計する
    SELECT
      message_id,
      is_test,
      is_spam,
      word,
      COUNT(*) AS cnt
    FROM
      clean_words
    GROUP BY
      message_id, is_test, is_spam, word
  ),

  -- ==========================================
  -- 2. モデルパラメータの学習
  --  * クラス別単語確率 log P(w | y) を求める
  --  * 非スパム/スパムの登場確率 P(y) を求める
  -- ==========================================
  train_data AS (
    SELECT
      *
    FROM count_words
    WHERE is_test = 0
  ),
  -- 2-1. クラス別単語頻度を集計 → log P(w | y) を求める
  count_by_word_train AS (
    -- 非スパム/スパム別に単語ごとの登場回数 N_{0,k}, N_{1,k} を計算する
    SELECT
      word,
      SUM(IF(is_spam = 0, cnt, 0)) AS cnt_in_y0,  -- N_{0,k}
      SUM(IF(is_spam = 1, cnt, 0)) AS cnt_in_y1,  -- N_{1,k}
    FROM train_data
    GROUP BY word
  ),
  count_total_words_train AS (
    -- 非スパム/スパム全体の合計単語数 N_0, N_1 と、学習データに登場する単語のユニーク数 K を計算する
    SELECT
      SUM(cnt_in_y0) AS total_cnt_in_y0,  -- N_0
      SUM(cnt_in_y1) AS total_cnt_in_y1,  -- N_1
      COUNT(*) AS count_unique_words  -- K
    FROM
      count_by_word_train
  ),
  calc_logprob_of_words AS (
    -- 単語ごとに条件付き登場確率を計算し対数をとる log P(w | y)
    SELECT
      *,
      LOG(cnt_in_y0 + ALPHA) - LOG(total_cnt_in_y0 + count_unique_words * ALPHA)
        AS logprob_word_in_y0,  -- log P(w | y=0)
      LOG(cnt_in_y1 + ALPHA) - LOG(total_cnt_in_y1 + count_unique_words * ALPHA)
        AS logprob_word_in_y1,  -- log P(w | y=1)
    FROM count_by_word_train, count_total_words_train
  ),
  calc_log_prob_for_smoothing AS (
    -- 学習データに登場しなかった単語については、P(w | y) を alpha / (N_y + K alpha) で代用する
    SELECT
      LOG(ALPHA) - LOG(total_cnt_in_y0 + count_unique_words * ALPHA)
        AS logprob_for_smoothing_in_y0,
      LOG(ALPHA) - LOG(total_cnt_in_y1 + count_unique_words * ALPHA)
        AS logprob_for_smoothing_in_y1,
    FROM
      count_total_words_train
  ),
  -- 2-1. 各クラスの登場頻度から、非スパム/スパムの登場確率 P(y) を求める
  calc_spam_prob_train AS (
    SELECT
      COUNT(DISTINCT IF(is_spam = 0, message_id, NULL))
        / COUNT(DISTINCT message_id) AS p_y0,
      COUNT(DISTINCT IF(is_spam = 1, message_id, NULL))
        / COUNT(DISTINCT message_id) AS p_y1,
    FROM
      train_data
  ),

  -- ==========================================
  -- 3. テストデータに対して推論計算
  -- ==========================================
  test_data AS (
    SELECT
      *
    FROM
      count_words
    WHERE is_test = 1
  ),
  join_model_params_to_test_data AS (
    -- 各テストデータに含まれる単語に、学習データで計算した log P(w | y) を紐づける
    -- テストデータで新たに登場した単語については、平滑化により求めた値で置き換える（ゼロ頻度問題の回避）
    SELECT
      message_id,
      word,
      cnt,  -- n_k
      COALESCE(logprob_word_in_y0, logprob_for_smoothing_in_y0)
        AS logprob_word_in_y0,  -- log P(w_k | y=0)
      COALESCE(logprob_word_in_y1, logprob_for_smoothing_in_y1)
        AS logprob_word_in_y1,  -- log P(w_k | y=1)
    FROM test_data
    LEFT JOIN
      calc_logprob_of_words
      USING (word)
    CROSS JOIN calc_log_prob_for_smoothing
  ),
  calc_llr_sum_for_each_message AS (
    -- メッセージごとに、対数尤度比 log P(w_k | y=1) - log P(w_k | y=0) の合計を計算する
    SELECT
      message_id,
      SUM(cnt * (logprob_word_in_y1 - logprob_word_in_y0))
        AS llr_sum  -- Σ_k n_k {log P(w_k | y=1) - Σ log P(w_k | y=0)}
    FROM
      join_model_params_to_test_data
    GROUP BY message_id
  ),
  calc_spam_prob_test AS (
    -- スパム予測確率 P(y=1 | d) を計算する
    SELECT
      *,
      SAFE_DIVIDE(1, 1 + EXP(-llr_sum) * p_y0 / p_y1)
        AS spam_prob  -- P(y=1 | d)
    FROM calc_llr_sum_for_each_message
    CROSS JOIN calc_spam_prob_train
  )

-- ==========================================
-- 4. 予測結果と元データを紐づける
-- ==========================================
SELECT
  message_id,
  spam_prob,
  is_spam,
  message
FROM calc_spam_prob_test
JOIN preprocessed_sms_dataset
  USING (message_id)
ORDER BY message_id

 モデル評価ここまでで、各メッセージに対してスパム確率を出力できるようになりました。

せっかくですので、実際のスパムメッセージデータセットで計算したこの確率を用いて、モデルの性能を評価してみます。
まずは、予測値を 0.05幅のビンで区切って、その中に含まれるデータの数とスパムラベルの割合を集計してみました。

その結果、ものの見事予測確率0.95以上にスパムデータが集中していることがわかりました。


予測スパム確率
メッセージ件数
スパム件数
スパム割合


(0.95, 1.0]
125
123
0.984

(0.9, 0.95]
4
1
0.25

(0.85, 0.9]
1
0
0.0

(0.8, 0.85]
1
0
0.0

(0.75, 0.8]
4
0
0.0

(0.7, 0.75]
0
0
<NA>

(0.65, 0.7]
1
0
0.0

(0.6, 0.65]
1
1
1.0

(0.55, 0.6]
0
0
<NA>

(0.5, 0.55]
1
1
1.0

(0.45, 0.5]
1
0
0.0

(0.4, 0.45]
1
0
0.0

(0.35, 0.4]
5
0
0.0

(0.3, 0.35]
3
0
0.0

(0.25, 0.3]
2
0
0.0

(0.2, 0.25]
4
0
0.0

(0.15, 0.2]
5
0
0.0

(0.1, 0.15]
8
1
0.125

(0.05, 0.1]
7
0
0.0

(-0.001, 0.05]
819
6
0.0073260

きちんと精度評価をしてみた結果が以下になります。
ROC AUC: 0.98
Average Precision (AP): 0.97
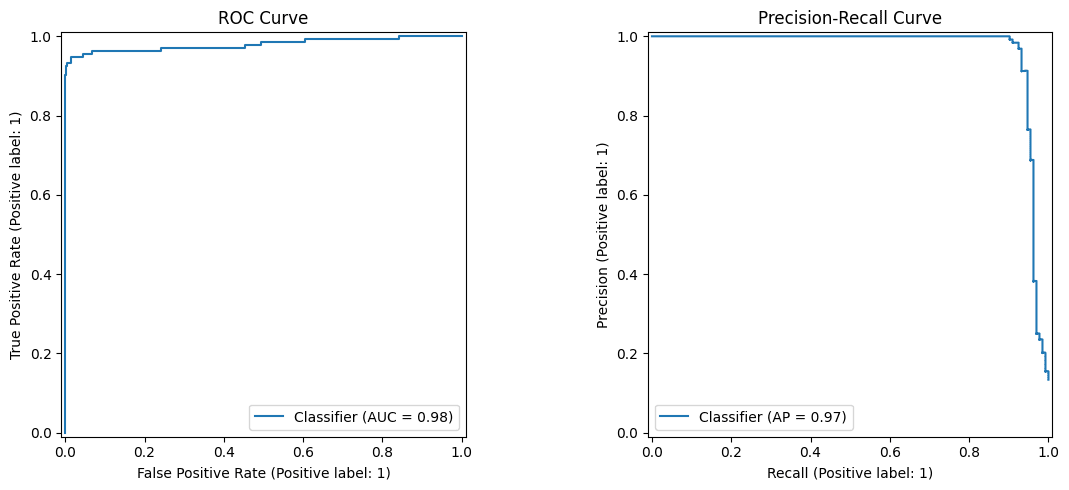
加えて、スパム検知では「スパムを取り逃がさないこと」と「誤ってスパムと判定しないこと」の両方が重要なため、ここでは precision・recall・F1-score の3つを用いて評価します。
閾値を0.95としたときの分類精度評価指標は以下のようになっていました：
precision: 0.98
→ モデルがスパムと判定したメッセージのうち、98%が実際にスパムだった

recall: 0.92
→ 実際のスパムメッセージ全体のうち、92%をスパムとして検出できた

F1-score: 0.95
→ precision と recall がトレードオフになる状況で、両者のバランスを表す指標

混同行列（confusion matrix）は以下の通りです：

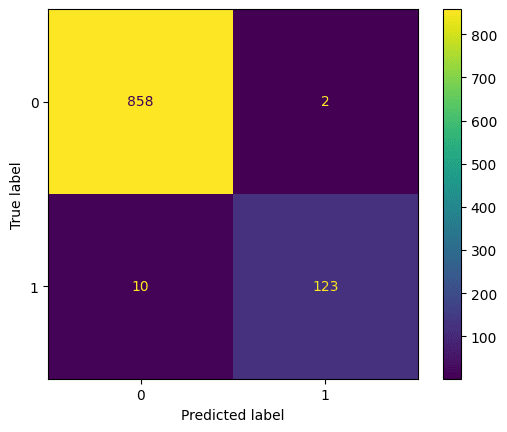
シンプルな手法にも関わらず、数字的になかなかいい感じですね！
なお、予測が外れた箇所ですが、以下のような傾向がありました：
スパムラベルがついていないにも関わらず、スパム予測確率が高かった箇所
スラングや機種依存文字（文字化けしている）が多い
文章が短い

スパムラベルがついているが、スパム予測確率が低かった箇所
ラベルが誤って振られている（実際はスパムではない普通の会話）
内容的にはスパム広告だが、文章が人の目で見ても自然
複数単語をスペースを空けず繋げて書いている（新規登場単語として判定されてしまう）


 おまけところで、昨今AIによる予測結果の説明可能性がしばしば話題になりますが、

今回の手法ではどの単語が予測結果に寄与したかを算出することができます。
もう一度予測値の計算式(5)を見てみましょう：

\begin{aligned}
    \hat{P}(y=1 \vert \boldsymbol{d}_0)
    &= \frac{1}{1 + \frac{\hat{P}(y=0)}{\hat{P}(y=1)}\exp \left\{-\sum_{k=1}^{K'} n_{0,k}\log\frac{\hat{P}(w_k \vert y=1)}{\hat{P}(w_k \vert y=0)}\right\}}\\
\end{aligned}
上記の式の指数関数部分の中にある以下に着目します：

\sum_{k=1}^{K'} n_{0,k}\log\frac{\hat{P}(w_k \vert y=1)}{\hat{P}(w_k \vert y=0)}.
これは、単語ごとの対数尤度比（≒ その単語がスパム文書に現れやすいかどうかを表す指標）の総和を、全単語で合計したものです。

この値が大きくなるほどスパム予測確率は大きくなり、小さくなるほど予測確率は小さくなります。

従って、予測対象メッセージに含まれる各単語について対数尤度比の合計 n_{0,k} \log\frac{\hat{P}(w_k \vert y=1)}{\hat{P}(w_k \vert y=0)} を計算し、絶対値の大きい単語から順に並べてみるといいでしょう。

この値が大きく正の値を取っていればその単語はスパム確率を押し上げていて、値がマイナスに触れていれば逆に非スパム側に貢献していると解釈することができます。
実際にテストデータ全体で各単語の対数尤度比を集計してみたところ、

正の値側では prize や claim、金額表現、短縮コードといった典型的なスパム特有の単語が上位に並びました。

一方で負の値側を見ると、he や she といった単語が非スパム側に強く寄与していました。

このことからも、ナイーブベイズが「意味」を理解しているというよりも、

「クラス間（スパム/非スパム）で統計的に強く偏った単語」を拾い上げていることが見て取れます。

 まとめ一見難しそうなナイーブベイズ分類でしたが、コメント含めても200行程度のクエリで書くことができましたね。

SQL でも少し頑張れば機械学習・統計モデルを作れるのです！
ちなみに、以前こちらの記事では BigQuery で単回帰モデルを作る方法を紹介しました。

https://note.com/tatatamiya/n/ncb54f4bf2dd4
上記の単回帰の記事では一部 BigQuery の独自機能を使いましたが[2]、今回のナイーブベイズは、多少頑張れば BigQuery 以外の SQL でも実行することができます。

ただし、学習データ・テストデータへの分割や、メッセージを単語に分割して単語ごとにカウントする処理は、DB によっては実行できない場合があります。
そのような場合は、単語ごとの集計部分までを別の環境で実行してからテーブル化し、その後のモデル学習・予測部分を SQL で書くのが良いでしょう。
また、今回はナイーブベイズ分類の代表的な応用例としてスパム検知を題材にしましたが、同様の考え方は他のタスクにも応用できます。

例えばECサイトの購買データであれば、単語の出現回数を商品の購入回数に置き換えることで、ユーザー行動の分類といった用途にも利用できます。
より精密な予測が求められる場合にはディープラーニングや勾配ブースティング木といった高度な手法を用いた方が無難ですが、R や Python を立ち上げるのが面倒な場合、もしくは運用上 SQL だけでなんとか分類モデルを作る必要がある場合などには、ナイーブベイズも試してみる価値があるかもしれません。

 参考文献Spam Filtering with Naive Bayes https://www.kaggle.com/code/pavelbogdanov/spam-filtering-with-naive-bayes
本記事で用いたのと同じスパムメッセージデータセットで、Python によりナイーブベイズモデルを作成している Kaggle notebook です。

scikit-learn User Guide https://scikit-learn.org/stable/modules/naive_bayes.html
Python の機械学習ライブラリ scikit-learn のナイーブベイズのユーザーガイドです。
本記事では触れませんでしたが、ナイーブベイズにも種類があり、今回でいう単語登場回数のようなカテゴリごとのカウントデータを用いたものは multinomial naive bayes と呼ばれます。Multinomial の他にも、連続値をもとに予測する Gaussian Naive Bayes といった手法もあります。

Naive Bayes Classifier in Wikipedia https://en.wikipedia.org/wiki/Naive_Bayes_classifier
ナイーブベイズの背景・理論的側面がコンパクトにまとまっています。

持橋 大地、統計的テキストモデル（岩波書店、2025）https://www.iwanami.co.jp/book/b10135026.html
5.1節にナイーブベイズによる文書分類の解説があります。
全体を通して文字→単語→文→文章の順でテキストを統計的に扱う際の考え方が丁寧に解説されています。社内のデータサイエンティストで輪読しましたが、とても勉強になりました。


脚注
理論的にはこのような平滑化は、事前分布として対称なディリクレ分布を仮定して単語の事後分布を計算し、それをもとに単語登場率の期待値を求めることに一致します。特に \alpha=1 の場合をラプラス平滑化（Laplace Smoothing）といいます。https://en.wikipedia.org/wiki/Additive_smoothing ↩︎
一応 BigQuery の機能を使わなくても単回帰モデルは作れますが、クエリがかなり複雑になると思われます。 ↩︎
求めたいもの	必要な集計値	集計値の説明
式(4) スパム/非スパムメールにおける各単語の推定登場確率 $\hat{P}(w_k \vert y) = \frac{N_{y,k} + \alpha}{N_y + K\alpha}$	$\left\{ N_{1,k}, N_{0,k}\right\}_{k=1}^K$	スパム/非スパムメール中の各単語 $w_k$ の登場回数
	$N_1, \, N_0$	スパム/非スパムメールに含まれる単語総数
	$K$	学習データ全体に含まれる単語のユニーク数
式(2) スパム/非スパムメールの推定割合 $\hat{P}(y=1) = \frac{1}{D}\sum_{i=1}^D y_i, \quad \hat{P}(y=0) = \frac{1}{D}\sum_{i=1}^D (1 - y_i)$	$D$	学習データ数
	$\sum_{i=1}^D y_i, \, \sum_{i=1}^D (1-y_i)$	学習データ中のスパムメール数・非スパムメール数
式(5) 推定スパム率 $\hat{P}(y=1\vert \boldsymbol{d_0})=\frac{1}{1 + \frac{\hat{P}(y=0)}{\hat{P}(y=1)}\exp \left\{-\sum_{k=1}^{K'} n_{0,k} \log\frac{\hat{P}(w_k \vert y=1)}{\hat{P}(w_k \vert y=0)}\right\}}$	$\{n_{0,k}\}_{k=1}^{K'}$	予測対象メールの文中に含まれる各単語 $\{w_k\}_{k=1}^{K'}$ の登場回数
	データ型	内容	例
カラム1	STRING	正解ラベル (`spam` ... 13%, `ham` ... 87%)	spam
カラム2	STRING	メッセージ文面 (5169種類)	This is the 2nd time we have tried 2 contact u...
message_id	is_spam	message	is_test
1	0	Hoge fuga piyo fuga.	0
2	0	Piyo piyo hoge HOO :)	0
3	0	HOGE inc. meeting at 10.	1
4	1	WIN!!! CLICK HOO TO CLAIM NOW!	0
5	1	Click PIYO to win PiYo!!!	1
message_id	is_test	is_spam	word	cnt
1	0	0	hoge	1
1	0	0	fuga	2
1	0	0	piyo	1
2	0	0	hoge	1
2	0	0	piyo	2
2	0	0	hoo	1
2	0	0	:)	1
3	1	0	hoge	1
3	1	0	inc	1
3	1	0	meeting	1
3	1	0	at	1
3	1	0	10	1
4	0	1	win	1
4	0	1	click	1
4	0	1	hoo	1
4	0	1	to	1
4	0	1	claim	1
4	0	1	now	1
5	1	1	click	1
5	1	1	piyo	2
5	1	1	to	1
5	1	1	win	1
message_id	is_spam	word	cnt
1	0	hoge	1
1	0	fuga	2
1	0	piyo	1
2	0	hoge	1
2	0	piyo	2
2	0	hoo	1
2	0	:)	1
4	1	win	1
4	1	click	1
4	1	hoo	1
4	1	to	1
4	1	claim	1
4	1	now	1
word	cnt_in_y0	cnt_in_y1
:)	1	0
claim	0	1
click	0	1
fuga	2	0
hoge	2	0
hoo	1	1
now	0	1
piyo	3	0
to	0	1
win	0	1
total_cnt_in_y0	total_cnt_in_y1	count_unique_words
9	6	10
word	log_prob_word_in_y0	log_prob_word_in_y1
:)	-2.25129	-2.77259
claim	-2.94444	-2.07944
click	-2.94444	-2.07944
fuga	-1.84583	-2.77259
hoge	-1.84583	-2.77259
hoo	-2.25129	-2.07944
now	-2.94444	-2.07944
piyo	-1.55814	-2.77259
to	-2.94444	-2.07944
win	-2.94444	-2.07944
log_prob_word_in_y0	log_prob_word_in_y1
-2.94444	-2.77259
p_y0	p_y1
0.666667	0.333333
message_id	is_test	is_spam	word	cnt
3	1	0	hoge	1
3	1	0	inc	1
3	1	0	meeting	1
3	1	0	at	1
3	1	0	10	1
5	1	1	click	1
5	1	1	piyo	2
5	1	1	to	1
5	1	1	win	1
message_id	word	cnt	log_prob_word_in_y0	log_prob_word_in_y1
3	hoge	1	-1.84583	-2.77259
3	inc	1	-2.94444	-2.77259
3	meeting	1	-2.94444	-2.77259
3	at	1	-2.94444	-2.77259
3	10	1	-2.94444	-2.77259
5	click	1	-2.94444	-2.07944
5	piyo	2	-1.55814	-2.77259
5	to	1	-2.94444	-2.07944
5	win	1	-2.94444	-2.07944
message_id	llr_sum	p_y0	p_y1	spam_prob
3	-0.239361	0.666667	0.333333	0.282416
5	0.166104	0.666667	0.333333	0.371207
message_id	spam_prob	is_spam	message
3	0.282416	0	HOGE inc. meeting at 10.
5	0.371207	1	Click PIYO to win PiYo!!!
予測スパム確率	メッセージ件数	スパム件数	スパム割合
(0.95, 1.0]	125	123	0.984
(0.9, 0.95]	4	1	0.25
(0.85, 0.9]	1	0	0.0
(0.8, 0.85]	1	0	0.0
(0.75, 0.8]	4	0	0.0
(0.7, 0.75]	0	0	<NA>
(0.65, 0.7]	1	0	0.0
(0.6, 0.65]	1	1	1.0
(0.55, 0.6]	0	0	<NA>
(0.5, 0.55]	1	1	1.0
(0.45, 0.5]	1	0	0.0
(0.4, 0.45]	1	0	0.0
(0.35, 0.4]	5	0	0.0
(0.3, 0.35]	3	0	0.0
(0.25, 0.3]	2	0	0.0
(0.2, 0.25]	4	0	0.0
(0.15, 0.2]	5	0	0.0
(0.1, 0.15]	8	1	0.125
(0.05, 0.1]	7	0	0.0
(-0.001, 0.05]	819	6	0.0073260
Money Forward DevelopersPublication
株式会社マネーフォワード公式開発者向けアカウントです。技術記事やイベント、登壇など技術関連のことを発信します。
SQLだけでナイーブベイズ分類モデルを実装する ― スパムメール分類を例に

ナイーブベイズとは？

理論

問題設定

ベースとなる考え方

「ナイーブ」な独立性の過程

Bag-of-Words による表現

実データでのモデル学習方法

条件付き単語出現確率 $P(w_k \vert y)$ の推定

各ラベルの出現確率 $P(y)$ の推定

実装上の補足

ゼロ頻度問題の回避

数値のアンダーフロー回避

SQL による実装

使用データセット

0. データ読み込み + 前処理

1. メッセージごとに各単語の登場回数を集計

2. モデルパラメータの学習

3. テストデータに対して推論計算

4. 予測結果と元データを紐づける

クエリ全貌

モデル評価

おまけ

まとめ

参考文献

Discussion
