README

O'Reilly Japan - コンピュータシステムの理論と実装

https://www.nand2tetris.org/demos

写経リポジトリ

進め方

開催実績

2022/01/03(月) https://zenn.dev/link/comments/923b06c53129bf
2022/01/10(月) https://zenn.dev/link/comments/3a6fe14fd47031
2022/01/17(月) https://zenn.dev/link/comments/9efce3e4133270

mohira

2022/01/03(月)

やったこと

まえがき
環境構築

MEMO

コンピュータをマジでゼロからつくる！
NANDからはじめる
テンションが高まる、まえがき
読書会じゃなくて、俺達は、大学に通っている気持ち

次回開催メモ

xix 「イントロダクション」から

mohira

環境構築

付録CどおりやればOK。

https://drive.google.com/open?id=1xZzcMIUETv3u3sdpM_oTJSTetpVee3KZ からダウンロードして、シェルスクリプト実行でOK。

$ cd nand2tetris
$ chmod +x tools/*.sh
$ ./tools/HardwareSimulator.sh &

mohira

2022/01/10(月)

やったこと

xix 「イントロダクション」からp.12 HDLでのXOR実装まで

MEMO

本書の全体感とか流れ
ブール代数 / ブール式 / ブール関数 / 正準表現
NANDがあれば、NANDもできる！
抽象化 / インタフェースと実装
Hello HDL!!! たのしい

次回開催メモ

p.13 仕様

jnuank

本書では3つを学ぶ

「コンピュータの動く仕組み」「複雑な問題を扱いやすいモジュールに分
割する方法」そして「ハードウェアとソフトウェアからなる巨大なシステムを開発す
る方法」

mohira

それは、「コンピュータの動く仕組み」「割する方法」そして「ハードウェアとソフトウェアからなる巨大なシステムを開発する方法」である。

wkwk

mohira

一方、コンピュータサイエンスの分野で「抽象化」という言葉が使われる場合は、次のように非常に具体的な意味合いで使われる。それは「この要素は何をするのか（what）」だけを考え、その詳細である「それをどのように行うのか（how）」は無視するということである。

ここまで言い換えられるか。確かに。

この機能部分のみを記述するためには、その要素に関係のない情報は含めずに、それを使うために必要な情報はすべて記載する。つまり、その要素の実装部分にかかわる情報は、 それを使おうとするユーザーの目に触れてはならない 。なぜなら、ユーザーにとってそれは意味のない情報だからである。

隠すならちゃんと隠す。隠してこその、抽象化

jnuank

機械語もまた抽象化されたものであり、物理的には存在しない。

たしかに。

jnuank

ところで、標準言語ライブラリとは何だろうか？そして、オペレーティングシステ
ム（ OS ）はどのように動いているのだろうか？これらの問は 12 章で扱われるテーマ
である。

たしかに。あまり考えたことがなかったな。
12章が楽しみだ。

jnuank

一般的にコンパイルには、コンパイラ、バーチャルマシン、アセンブラの 3 つの変換器が関連する。

そうなの？　コンパイラだけが全部やってくれるんじゃないのか

mohira

バーチャルマシン、まじで謎。知りたい。

jnuank

コンパイラが、高水準言語のコードから中間コードを生成する。
変換作業は、構文解析とコード生成

jnuank

思量

jnuank

ブール関数の表現

真理値表
ブール式
- f (x, y, z) = (x + y) · z̄
正準表現
- f (x, y, z) = x̄yz̄ + xȳz̄ + xyz̄

mohira

正準表現（canonical representation）
重要な結論を導く。それは、どのようなブール関数であれ、たとえそれがどれだけ複雑であったとしても、3 つのブール演算 And、Or、Not を用いて表現できる、ということである。

これが正準表現の威力！

直観的には納得できる話。

mohira

Equivalence 【ɪkwív(ə)ləns(米国)】

mohira

Nand 関数は（Nor 関数も同様に）、理論的に興味深い性質を持っている。それは、 And、Or、Not はそれぞれ Nand（または Nor）だけから作ることができるという点である。たとえば、x Or y = (x Nand x) Nand (y Nand y) というように、Nand だけから Or を作ることができる。

証明した！

また、正準表現を用いることで、すべてのブール関数は And、Or、Not の操作によって作ることができた。そのため、すべてのブール関数は Nand だけから作れることになる。

NAND最強！

mohira

ここで注意すべきは、ゲートのインターフェイスはただひとつしか存在しない、ということである。

ここから考えられるのは、

インターフェイスの設計がひどいと、おそらく悪いことになるし、
インターフェイスの設計が良いと、嬉しい。

mohira

ゲートの設計と実装の話は抽象化の説明として良いな〜

jnuank

HDLすごいな…

mohira

Xor.hdl

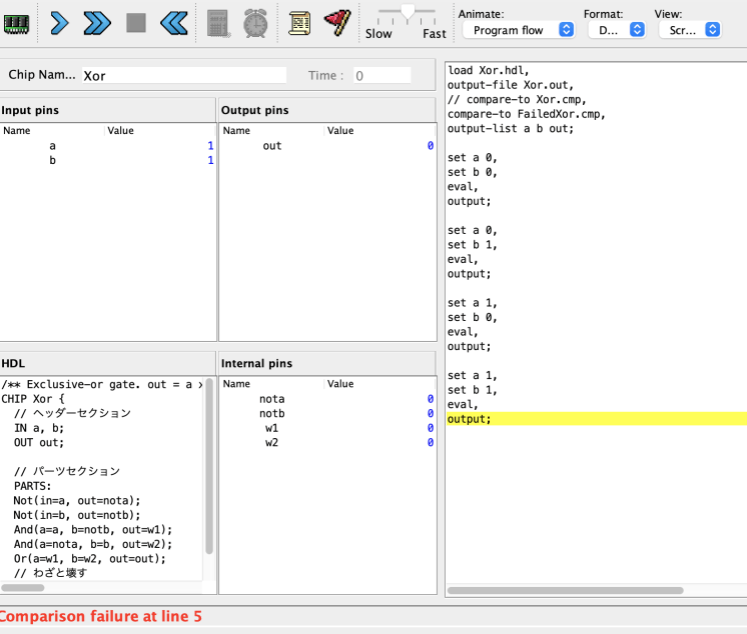
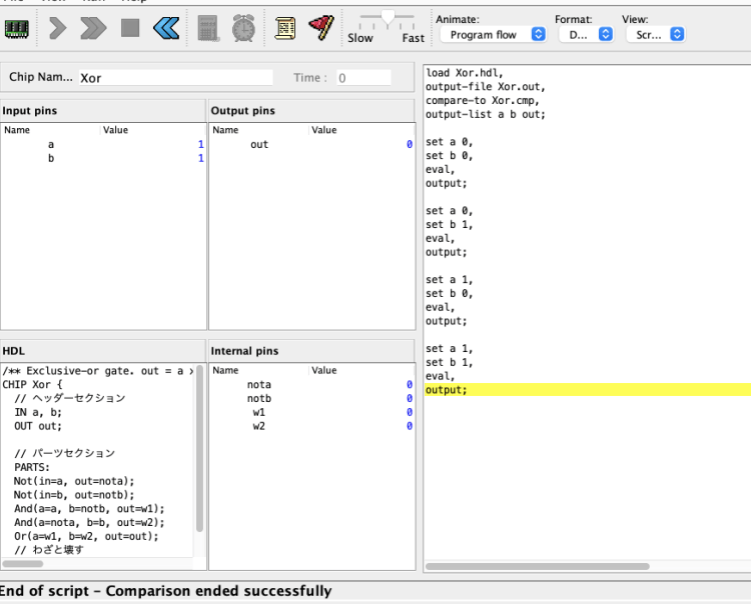
/** Exclusive-or gate. out = a xor b */
CHIP Xor {
  // ヘッダーセクション
  IN a, b;
  OUT out;

  // パーツセクション
  PARTS:
  Not(in=a, out=nota);
  Not(in=b, out=notb);
  And(a=a, b=notb, out=w1);
  And(a=nota, b=b, out=w2);
  Or(a=w1, b=w2, out=out);
  // わざと壊す
  // And(a=w1, b=w2, out=out);
}

Xor.tst

load Xor.hdl,
output-file Xor.out,
// compare-to Xor.cmp,
compare-to FailedXor.cmp,
output-list a b out;

set a 0,
set b 0,
eval,
output;

set a 0,
set b 1,
eval,
output;

set a 1,
set b 0,
eval,
output;

set a 1,
set b 1,
eval,
output;

Xor.out

a | b | out
0 | 0 | 0
0 | 1 | 1
1 | 0 | 1
1 | 1 | 0

Xor.cmp

a | b | out
0 | 0 | 0
0 | 1 | 1
1 | 0 | 1
1 | 1 | 0

FailedXor.cmp

| a | b |out|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |

jnuank

流れとしては、
ブール関数は、ブール式は正準表現などでAnd、Or、Notで構成することができる。

さらに言うと、And、Or、NotはNANDだけで全て表現ができることを証明したので、
コンピュータの最小構成要素はNAND、という説明だった

mohira

2022/01/17(月)

やったこと

p.12 1.1.5 〜 p.22 Xorの実装まで

MEMO

正準表現を使うと、ロジカルに、任意の回路の論理式をつくれる！
- 回路の作り方 → https://zenn.dev/link/comments/3e0fa45fc7fc16
HDLわかってきた感じある。
すぐに答えを見ないで、2人でちゃんと粘ったのは偉い！
リファクタリングでゲート節約
まじで、全部NANDでつくれてすごい
多入力と多ビットの違い → https://zenn.dev/link/comments/d1fe6ea3d04e64

次回開催メモ

p.22 マルチプレクサの実装から

mohira

このシミュレータを使い、最終的には汎用コンピュータを作るまでに至る。

まだ疑っている！

あるいは、「汎用コンピュータ」の定義が実は曖昧が原因。

mohira

NANDもできるNAND

この Nand ゲートから他のすべてのゲートが作成される。

mohira

1 入力の Not ゲートは「インバータ」とも呼ばれる。

「インバータ」って結構聞くよね。

jnuank

そのため、ここで述べるゲートは基本要素としてみなす必要はない。

Not, And, Or も最小構成要素ではない

jnuank

デマルチプレクサも基本ゲートか

mohira

コンピュータのハードウェアは「バス」と呼ばれる複数のビットからなる配列を操作するように設計されているのが一般的である。たとえば、32 ビットのコンピュータは 32 ビットのバス 2 本に対して And 関数を行う必要がある。

???

mohira

多ビットマルチプレ草

// 全部a か 全部b にする
if sel=0 {
  for i = 0..15 {
    out[i] = a[i]
  }  
} else {
  for i = 0..15 {
    out[i] = b[i]
  }
}

jnuank

多入力と多ビットの違いは？

mohira

・多ビットは、同じバスの他のビットに依存しない。演算が独立しているって感じ

・多入力は、入力すべてに依存するみたいなノリ

mohira

# Python風

def Mux4Way16(
  a[16],b[16],c[16],d[16], # バス幅16ビットで4入力"""
  sel[2] # セレクタは2つ (4 = log2(k) ∴ k = 2)
  ) -> out:
  if (sel[0], sel[1]) == (0, 0): # sel = 00
    for i=0..15:
        out[i] = a[i]
    
  elif (sel[0], sel[1]) == (0, 1): # sel = 01
    for i=0..15:
        out[i] = b[i]

  elif (sel[0], sel[1]) == (1, 0): # sel = 10
    for i=0..15:
        out[i] = c[i]

  elif (sel[0], sel[1]) == (1, 1): # sel = 11
    for i=0..15:
        out[i] = d[i]

jnuank

多入力多ビットマルチプレクサは、バス幅が変わろうがセレクタの数は特に変わらない。

m 入力 n ビットのマルチプレクサ。k個の制御ビット

k = log 2 m
制御ビット個数 = log2 入力数

※ log2n = 8 　→　n = 3

mohira

Not, And, Or の実装

jnuank

回路を作る考え方

真理値表を作る
正準表現を作る
回路を作る
Nandにすべて変換
テスト通す
リファクタ

mohira

XORの論理式を導いて、実装して、リファクタリングする流れの図解

正準表現 → 正準表現を回路図に起こす → 実装&テスト → リファクタリング

正準表現って、洗練されているっぽい式だけど、それを愚直にNANDだけで表現すると、無駄が生まれることもあるわけです！

p.22 Xorのリファクタリング: 正準表現を愚直にやったけど、Not(Not(x))があったので、回路を小さくできた · mohira/nand2tetris-shakyo@4a2477d

jnuank

一括リネーム

 ls -1 hoge* | awk -F"." '{print "mv "$0" fuga."$2}'   
mv hoge.json fuga.json
mv hoge.swp fuga.swp
mv hoge.txt fuga.txt

mohira

Xorのフォルダをベースに、新しいGateのフォルダを作る

cp -a Xor NewGate;  ls -1 Xor* | awk -F"." '{print "mv "$0" NewGate."$2}'    | sh

mohira

2022/01/24(月)

やったこと

p.22 マルチプレクサとデマルチプレクサの実装

MEMO

HDLのtstファイルの罠！
- 完全な文字列一致でやるので、半角スペースとかがおかしいとだめ！
- 左詰めとかに注意！
NAND4つでつくるデマルチプレクサをどうやって考えればいいか謎すぎる！未解決。

次回開催メモ

p.22 多ビット Not/And/Or ゲートから

mohira

マルチプレクサ

mohira

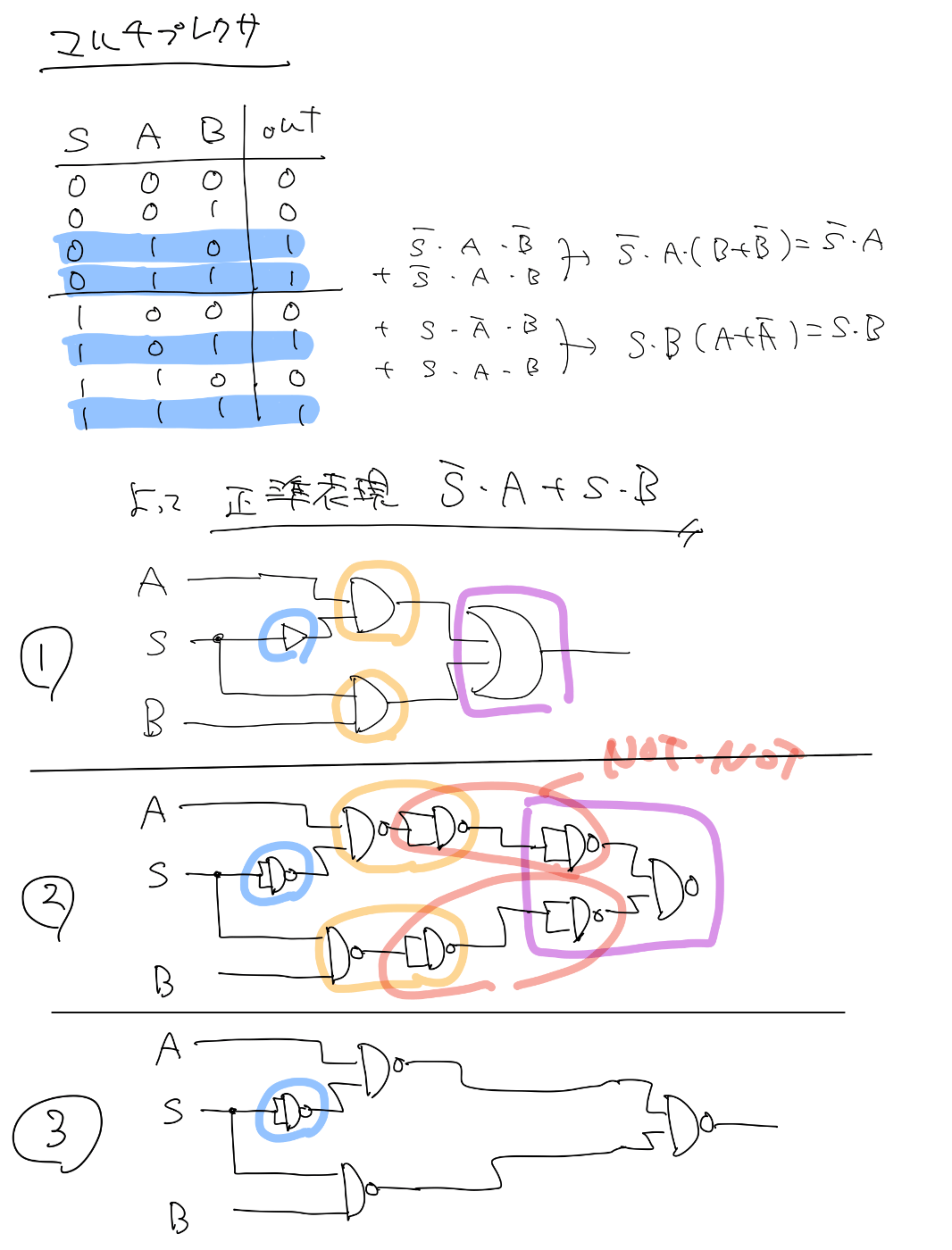
compareはマジの文字列単純一致だから、余計なスペースが入っていたりすると、テスト落ちるよ！

jnuank

ぱっと見わからんけども、代入して展開すると、とりあえず正準表現にはできそう

sel a out 
0   1  1  sel not * a 
0   0  0


sel b out 
1   1  1  sel * b 
1   0  0

mohira

tstファイルは1テストケースに付き1行で書いた方がめっちゃわかりやすい！

Multiplexer.tst

load Multiplexer.hdl,
output-file Multiplexer.out,
compare-to Multiplexer.cmp,
output-list s a b out;

set s 0, set a 0, set b 0, eval, output;
set s 0, set a 0, set b 1, eval, output;
set s 0, set a 1, set b 0, eval, output;
set s 0, set a 1, set b 1, eval, output;
set s 1, set a 0, set b 0, eval, output;
set s 1, set a 0, set b 1, eval, output;
set s 1, set a 1, set b 0, eval, output;
set s 1, set a 1, set b 1, eval, output;

mohira

↑
ジェネレーターつくろうよ？

jnuank

入力3つだと8通りあるんで、ブレース展開で生成

$ echo "set s "{0,1}", set a "{0,1}", set b "{0,1}" eval, output;\n"  
set s 0, set a 0, set b 0 eval, output;
 set s 0, set a 0, set b 1 eval, output;
 set s 0, set a 1, set b 0 eval, output;
 set s 0, set a 1, set b 1 eval, output;
 set s 1, set a 0, set b 0 eval, output;
 set s 1, set a 0, set b 1 eval, output;
 set s 1, set a 1, set b 0 eval, output;
 set s 1, set a 1, set b 1 eval, output;