Zenn
Closed4

UnityでIKを実装する

Unity
ik
mogesystemmogesystem

UnityでオレオレIK (Inverse Kinematics) を実装してみたい。

mogesystemmogesystem

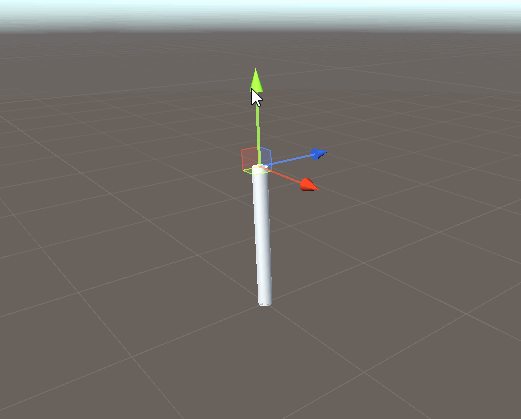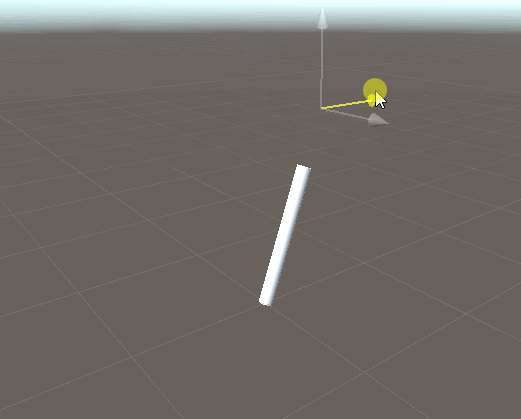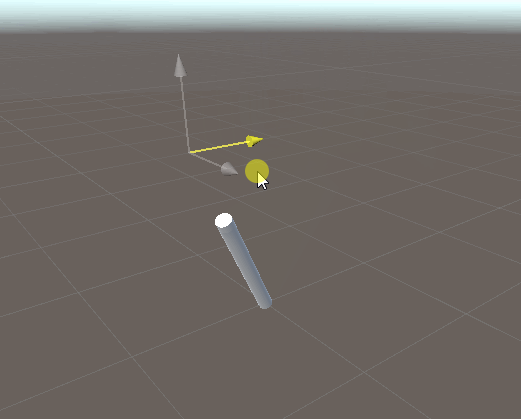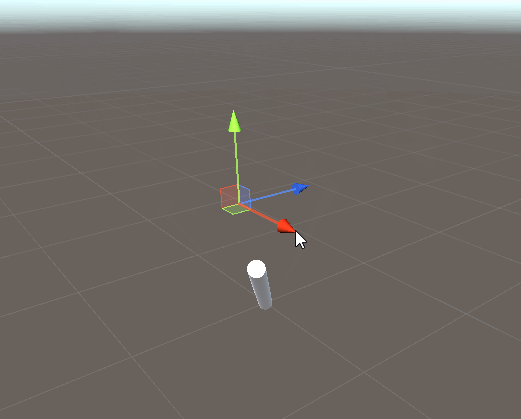
1ボーンのIKを実装してみる。

ボーンの「現在方向」と「目標方向」のズレを計算して、ズレている分だけ回転させる。
ベクトル間の回転角は Quaternion.FromToRotation で計算すればOK。

// SPDX-License-Identifier: Unlicense
using UnityEngine;

public class OneBoneIK : MonoBehaviour
{
    public Transform bone;     // 回転させたいボーン始点
    public Transform boneEnd;  // 回転させたいボーン終点
    public Transform target;   // ターゲットとするオブジェクト

    void Update()
    {
        var beforeDirection = boneEnd.position - bone.position;
        var afterDirection = target.position - bone.position;
        var delta = Quaternion.FromToRotation(beforeDirection, afterDirection);

        bone.rotation = delta * bone.rotation;
    }
}

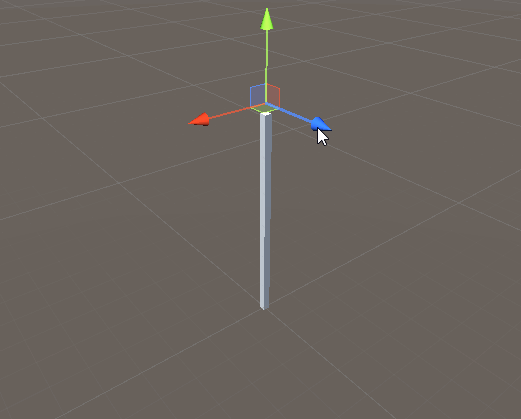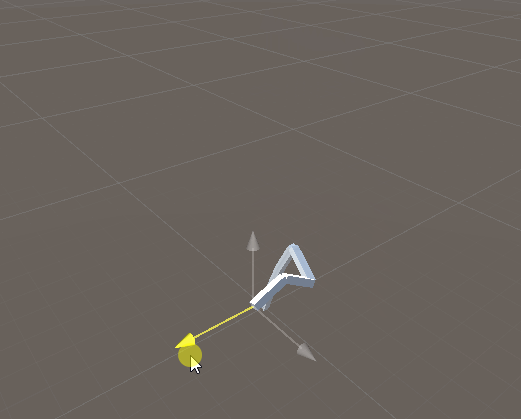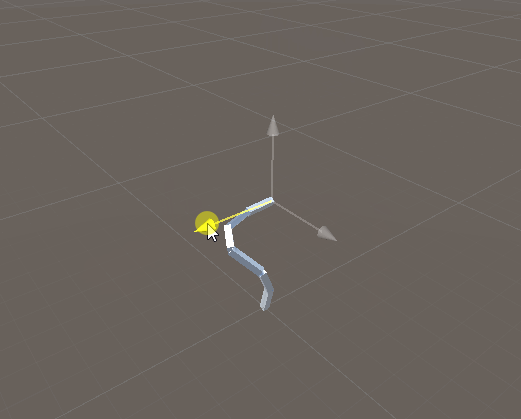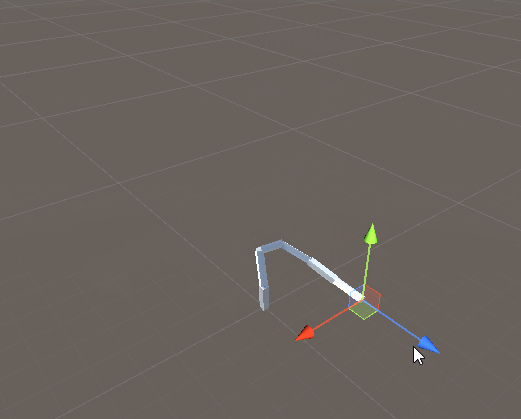
動作結果のスクリーンショット。1本の棒がターゲット座標を追いかける。

mogesystemmogesystem

2ボーンのシンプルなIKを実装してみる。
ここでは便宜上2つのボーンをそれぞれ「親ボーン」「子ボーン」と呼ぶことにする。

位置情報が確定している要素としては、親ボーンの始点（人間でいえば肩）と子ボーンの終点（人間でいえば手首）がある。始点はボーンの根本なので固定されているし、終点はIKターゲット位置と一致させることになる。
一方で、それらの間にあるジョイント（人間でいえば肘）の位置は確定していない。そこで2ボーンIKでは、このジョイントの位置を計算する。

ジョイントの座標は幾何学的に計算できる。
「親ボーンの終点」「子ボーンの始点」の可動範囲をそれぞれ考えてみると、どちらも球面になる。
ジョイントの位置は「親ボーンの終点」と「子ボーンの始点」がぴったり一致する座標なので、これら2つの球面が重なる境界線（円）を考えてみる。
この境界線上にある点なら、どこを選んでも適切なジョイント位置になる。

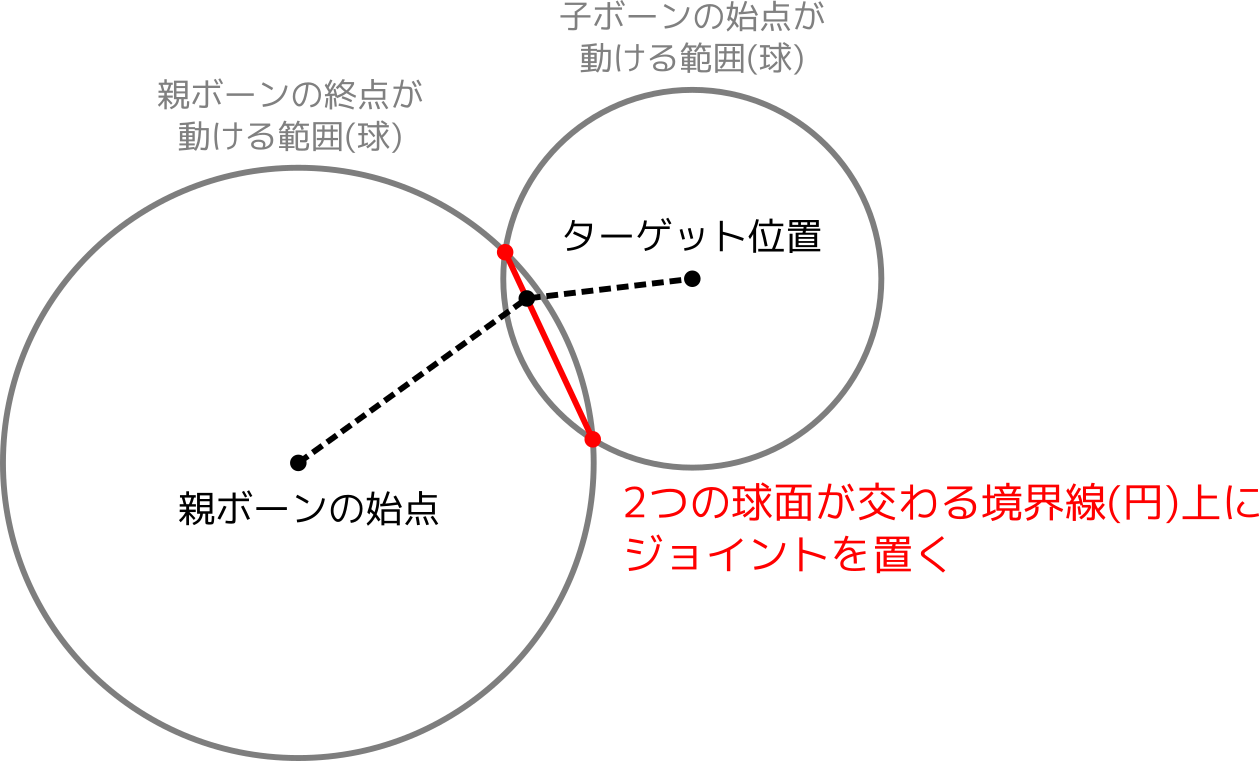
ここで新たな問題が浮上する。この境界線上のどこにジョイントを置くかを確定させなければならない。
よくあるIKソルバでは、ジョイントの曲げ方向を指示するベンドゴール（いわゆる肘IK）を使うことで、ジョイント位置をコントロールできるようにしている。ここではこの仕組みを真似てみる。

ベンドゴールの座標を平面へ射影すれば、円上のどの位置にジョイントを置くべきかが定まる。

実装してみる。

// SPDX-License-Identifier: Unlicense
using UnityEngine;

public class TwoBoneIK : MonoBehaviour
{
    public Transform bone1;    // 親ボーン
    public Transform bone2;    // 子ボーン
    public Transform boneEnd;  // 終点ボーン
    public Transform target;   // IKターゲットとするオブジェクト
    public Transform bendGoal; // 曲げ方向を指示するオブジェクト

    void Update()
    {
        // ジョイントの位置を求める
        var jointPosition = GetJointPosition();

        // 親ボーンをジョイントへ向ける
        var delta1 = GetDeltaRotation(bone1.position, bone2.position, jointPosition);
        bone1.rotation = delta1 * bone1.rotation;

        // 子ボーンをターゲットへ向ける
        var delta2 = GetDeltaRotation(jointPosition, boneEnd.position, target.position);
        bone2.rotation = delta2 * bone2.rotation;
    }

    Vector3 GetJointPosition()
    {
        var distance = Vector3.Distance(target.position, bone1.position);
        var length1 = Vector3.Distance(bone2.position, bone1.position);
        var length2 = Vector3.Distance(boneEnd.position, bone2.position);

        var straight = (target.position - bone1.position) / distance;

        // IKターゲットに届かない距離なら、一直線上に並べる
        if (distance <= Mathf.Abs(length2 - length1) || distance >= length1 + length2)
        {
            return straight * length1 + bone1.position;
        }

        // ジョイント可動中心
        var midLength = (length1 * length1 + distance * distance - length2 * length2) / (2 * distance);
        var midPoint = straight * midLength + bone1.position;

        // ジョイント可動半径
        var radius = Mathf.Sqrt(length1 * length1 - midLength * midLength);

        // ジョイント位置を平面上へ射影
        var bend = bendGoal.position - midPoint;
        var bendOnPlane = Vector3.ProjectOnPlane(bend, straight);
        bendOnPlane = bendOnPlane.normalized * radius;

        return bendOnPlane + midPoint;
    }

    Quaternion GetDeltaRotation(Vector3 origin, Vector3 current, Vector3 target)
    {
        // 始点と終点が近すぎたら回転させない
        if (Vector3.Distance(origin, target) < 1e-6)
            return Quaternion.identity;

        var beforeDirection = (current - origin).normalized;
        var afterDirection = (target - origin).normalized;
        return Quaternion.FromToRotation(beforeDirection, afterDirection);
    }
}

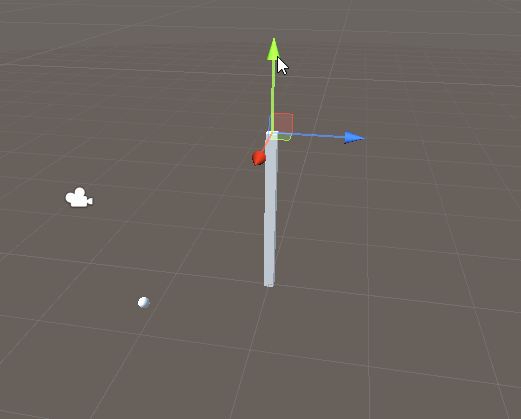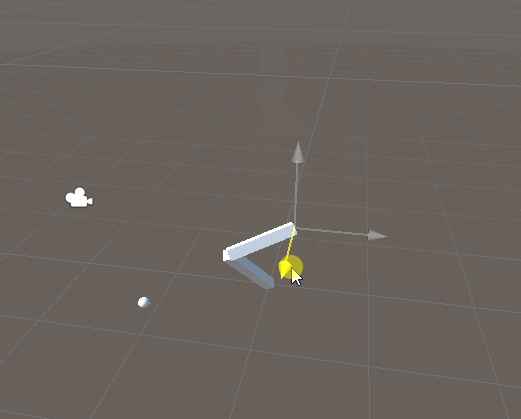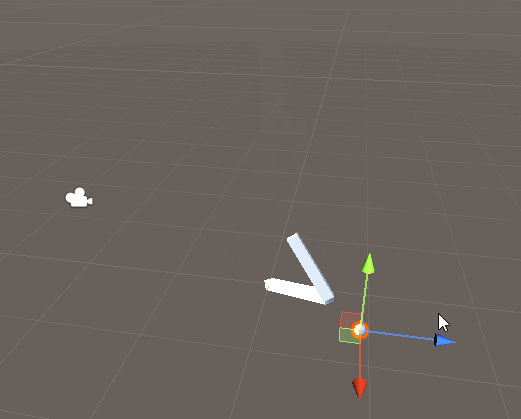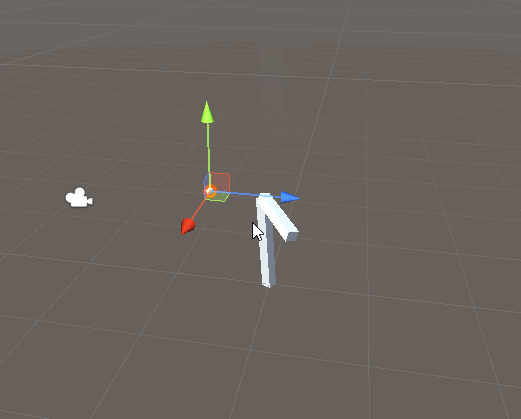
実行例。ちゃんと動いてるっぽい。

mogesystemmogesystem

複数ボーンIKの手法はいろいろある。

  • Jacobian IK: ヤコビ行列（各ボーンの角度を微小に動かしたときに先端位置がどれくらいズレるかを並べた行列）を用意して、ターゲット位置に合うようなボーン角度を逆算する。
  • CCD (Cyclic Coodinate Descent): 先端にあるボーンから順に角度を修正……を何度も繰り返す。
  • FABRIK (Forward and Backward Reaching Inverse Kinematics): 先端から根元、根元から先端……と交互に修正を繰り返す。

Jacobian IK は一発でボーン角度が決まるが、逆行列の計算が必要になり、数値計算ライブラリ (C# なら Math.NET や NumSharp) を使う必要がある。
CCD と FABRIK はシンプルな方法だが、必ずしも一度でボーンの角度が決まるわけではなく、何度か修正を繰り返す必要がある。

CCD や FABRIK によるボーンの角度の決め方は「自作CNCマシン・レーザーカッターについて」や「FABRIKによる逆運動学」にある図解が直感的にわかりやすい。

ここでは FABRIK を実装してみる。

// SPDX-License-Identifier: Unlicense
using System.Collections.Generic;
using UnityEngine;

public class FABRIK : MonoBehaviour
{
    public List<Transform> bones = new List<Transform>();
    public Transform target;
    public int maxIteration = 5;

    List<float> lengths = new List<float>();
    List<Vector3> positions = new List<Vector3>();

    void Awake()
    {
        // ボーンの長さ
        lengths.Clear();
        for (int i = 0; i < bones.Count - 1; i++)
        {
            lengths.Add(Vector3.Distance(bones[i].position, bones[i + 1].position));
        }

        // ボーンの位置
        positions.Clear();
        foreach (var b in bones)
        {
            positions.Add(b.position);
        }
    }

    void Update()
    {
        // 現在のボーン位置をコピーしてくる
        for (int i = 0; i < bones.Count; i++)
        {
            positions[i] = bones[i].position;
        }

        // FABRIKでボーン位置を推定
        var basePos = positions[0];
        var targetPos = target.position;
        var prevDistance = 0.0f;
        for (int iter = 0; iter < maxIteration; iter++)
        {
            // 収束チェック
            var distance = Vector3.Distance(positions[positions.Count - 1], targetPos);
            var change = Mathf.Abs(distance - prevDistance);
            prevDistance = distance;
            if (distance < 1e-6 || change < 1e-8)
            {
                break;
            }

            // Backward
            positions[positions.Count - 1] = targetPos;
            for (int i = positions.Count - 1; i >= 1; i--)
            {
                var direction = (positions[i] - positions[i - 1]).normalized;
                positions[i - 1] = positions[i] - direction * lengths[i - 1];
            }

            // Forward
            positions[0] = basePos;
            for (int i = 0; i <= positions.Count - 2; i++)
            {
                var direction = (positions[i + 1] - positions[i]).normalized;
                positions[i + 1] = positions[i] + direction * lengths[i];
            }
        }
        
        // 推定したボーン位置から回転角を計算
        for (int i = 0; i < positions.Count - 1; i++)
        {
            var origin = bones[i].position;
            var current = bones[i + 1].position;
            var target = positions[i + 1];
            var delta = GetDeltaRotation(origin, current, target);
            bones[i].rotation = delta * bones[i].rotation;
        }
    }
    
    Quaternion GetDeltaRotation(Vector3 origin, Vector3 current, Vector3 target)
    {
        var beforeDirection = (current - origin).normalized;
        var afterDirection = (target - origin).normalized;
        return Quaternion.FromToRotation(beforeDirection, afterDirection);
    }
}

実行例。ちゃんと動いてるっぽい。

このスクラップは2023/01/05にクローズされました