3Dアニメーションのための躍度最小軌道メモ

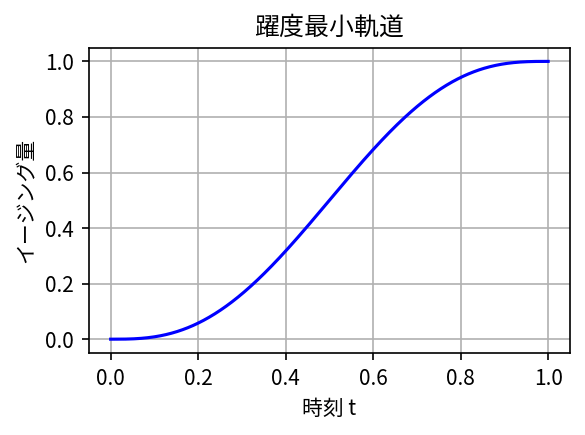
3DCGでキャラクターをプログラム制御したいとき、躍度最小軌道 (やくどさいしょうきどう) を使うと自然な動きになる。

断片的な情報を集めているうちになんとなく理解してきたのでまとめる。数式の導出も載せてみたが、ちょっとゴチャゴチャしてしまった。必要なところだけ読めばよいと思う。

かんたんに使う方法

イージング曲線（補間曲線）として以下の式を使うだけ。

モーションの開始時刻を $t=0$、終了時刻を $t=1$ としたとき、2点間の躍度最小軌道は、

$$f(t) = 6t^5 - 15t^4 + 10t^3$$

で表される。

グラフにするとこんな曲線になる。徐々に加速したあと徐々に減速する。キャラクターモーションを手付けした経験がある方には、“S字型の補間曲線”としてこうしたカーブに馴染みがあるかもしれない。

Unity向けにC#で実装するならこんな感じ。

float minJerkTrajectory(float t) {
    var tc = Mathf.Clamp01(t);  // 時刻の範囲を0～1に制限
    return ((6 * tc - 15) * tc + 10) * tc * tc * tc;
}

これをイージング曲線として使う。線形補間 (Lerp) なら次のように書ける。

// 位置の補間
var currentPos = Vector3.Lerp(positionFrom, positionTo, minJerkTrajectory(t));
// 角度の補間
var currentRot = Quaternion.Slerp(rotationFrom, rotationTo, minJerkTrajectory(t));

かんたんに使うときの注意点

(1) ここで紹介した式は2点補間にしか使えない。「静止状態」で始まって「静止状態」で終わるという条件で躍度最小軌道を求めると $6t^5 - 15t^4 + 10t^3$ が出てくる。これ以外のケース (たとえば、最初から動いた状態で始まる、複数点を経由するなど) では、別の式が躍度最小軌道になる。各条件での導出方法とリアルタイム計算の方法は、このあと解説していく。

(2) 外からかかる力が考慮されていない。たとえば手を鉛直方向に動かすときは腕に重力がかかるため、躍度最小軌道だと不自然に見えることがあるらしい (参考: 佐藤ら(2017))。後発の軌道モデル (トルク変化最小軌道など) ではこの点が解決されているが、より複雑な計算が必要になる。

このうち(1)の問題については、すこし別の導出方法をすることで、リアルタイムに躍度最小軌道を生成しながらキャラクター制御することができる。導出と実装方法を記事の後半で紹介する。

詳しく知りたい人向け

ただ2点補間するだけならここまでの情報で十分だと思われるが、もっと知りたい人向けに背景知識や導出方法の情報をまとめる。

躍度最小軌道はいかにして考案されたか

躍度最小軌道はもともと神経科学の研究で提案された。神経科学では「人間の手が描く運動の軌跡」を計測して分析する研究がおこなわれてきた。躍度最小軌道は、そうした手先軌道モデルのひとつである。

原典は以下の論文。
T. Flash and N. Hogan, "The coordination of arm movements: an experimentally confirmed mathematical model," Journal of Neuroscience, 5(7), pp.1688-1703, 1985.

実験参加者は机の上で操作子のハンドルを握り、ある点からほかの点へ線を引く（ペンタブを想像するとわかりやすいかも？）。このときのハンドルの位置や速度を計測する。

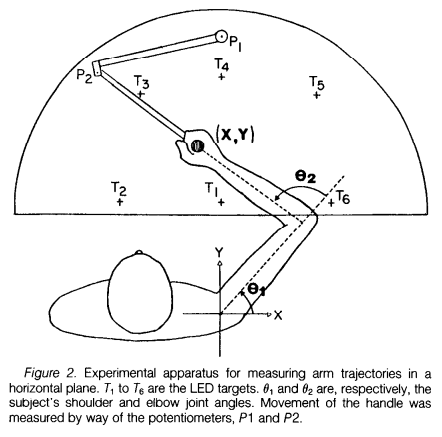
Flash and Hogan (1985) より。

こうした実験で速度変化を調べると、たいていだんだん加速して、線の真ん中あたりで最高速度に達し、終点に向かって減速するようなカーブが得られる。

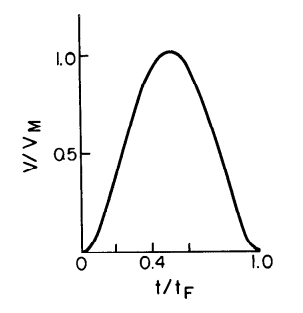
Flash and Hogan (1985) より。図の縦軸は速度。

これは手先運動の「速度変化」のグラフになっている。つまり、時間方向に積分することで冒頭のようなS字の「位置変化」のグラフとして得られる。

こうした手先運動の実測データによくあてはまる数学的モデルとして、先の論文で躍度最小軌道が提案されている。

数式による表現

まず 躍度 (やくど, 英:jerk) について説明する。力学の授業で習うように、時間変化する物体位置 $x(t)$ を時間で1階微分すると「速度」が出てくる。2階微分すると「加速度」になる。「躍度」はその3階微分バージョンである。

• 位置
  $$x(t)$$
• 速度 (1階微分)
  $$\frac{d x(t)}{d t}$$
• 加速度 (2階微分)
  $$\frac{d^2 x(t)}{d t^2}$$
• 躍度 (3階微分)
  $$\frac{d^3 x(t)}{d t^3}$$

躍度最小軌道は、その名のとおり「動作全体の躍度が最小になるような軌道」のことである。まずは「躍度が最小になる」ということを数式で表現してみる。ここでは 「躍度の小ささ」を評価する関数 $J(x(t), y(t))$ を次のように設定して、これを最小にする（なるべくゼロに近づける）ような曲線を計算することを考える。

$$J(x(t), y(t)) = \int_0^{T} \left[ \left( \frac{d^3 x(t)}{dt^3} \right)^2 + \left( \frac{d^3 y(t)}{dt^3} \right)^2 \right] dt$$

この式では躍度を二乗している。なぜそんなことをするかというと、躍度に負値があらわれたときに正値へ変換するためである。(二乗ではなく絶対値でよいのではと思うかもしれないが、ふつうの躍度最小軌道では後の導出をしやすくするために二乗を使う。)
負値が出ないようにすることで、この評価関数 $J(x(t), y(t))$ が最も小さくなる（つまりゼロに近づく）ような曲線が躍度最小軌道ということになる。

ここまでの内容をまとめる。評価値 $J$ を「躍度の二乗を開始時刻 $t=0$ から終了時刻 $t=T$ にわたって積分した値」として、これを最小にするような曲線 $x(t), y(t)$ が知りたい。

評価関数から躍度最小軌道へ

では、ここで式を立てた評価関数から具体的なカーブを計算するにはどうすればよいだろうか。そこで、評価関数が最小になるときに数学的にどんなことが言えるか考えてみる。

実は、評価関数 $J(x(t), y(t))$ が極小のとき、曲線 $x(t), y(t)$ の6階微分がゼロになることが示せる。(ここでは詳細を追わないが、導出は元論文の Appendix A に載っている。オイラー・ポアソン方程式を使う。)

$$\frac{d^6 x(t)}{dt^6} = 0, \frac{d^6 y(t)}{dt^6} = 0$$

曲線 $x(t), y(t)$ を6階微分するとゼロになる。すなわちこの曲線は5次多項式を使うことで十分に表現できる。

$$\begin{align*} x(t) &= \alpha_0 + \alpha_1 t + \alpha_2 t^2 + \alpha_3 t^3 + \alpha_4 t^4 + \alpha_5 t^5 \\ y(t) &= \beta_0 + \beta_1 t + \beta_2 t^2 + \beta_3 t^3 + \beta_4 t^4 + \beta_5 t^5 \\ \end{align*}$$

というのも、5次多項式は6階微分するとちょうどすべての項が消える（ゼロになる）からだ。

こうして、5次多項式で躍度最小軌道が表現できることがわかった。あとはこの多項式の係数 $\alpha_0, \alpha_1, \alpha_2, \alpha_3, \alpha_4, \alpha_5$ と $\beta_0, \beta_1, \beta_2, \beta_3, \beta_4, \beta_5$ を定めれば、躍度最小軌道 $x(t), y(t)$ が求められる。

躍度最小軌道の導出: 開始・終了時点で任意状態の場合

ここまでの結果を使って、開始・終了時点で特定の位置・速度・加速度が与えられている場合の躍度最小軌道を求める。

ここでは計算を簡単にするために、以下の前提を置くことにする。

• 1次元空間の場合として $x(t)$ のみを扱う
• 終了時刻を $T=1$ とする（時刻は解いたあとで適当にスケーリングすればよい）

まずは位置 $x$ の条件を考える。開始位置を $x_o$、終了位置を $x_f$ とすると、

$$\begin{align*} x(0) &= x_o \\ x(T) &= x_f \end{align*}$$

と書ける。

次に、速度 $\frac{d x}{d t}$ の条件を考える。初速を $v_o$、終了速度を $v_f$ とすると、

$$\begin{align*} \frac{d}{dt}x(0) &= v_o \\ \frac{d}{dt}x(T) &= v_f \end{align*}$$

と書ける。

同様に加速度 $\frac{d^2 x}{d t^2}$ についても、開始時加速度を $a_o$、終了時加速度 $a_f$ とすると、

$$\begin{align*} \frac{d^2}{dt^2}x(0) &= a_o \\ \frac{d^2}{dt^2}x(T) &= a_f \end{align*}$$

と書ける。

ここまでの6つの条件を組み合わせることで、6元連立方程式が立てられる。式中にあらわれる $x(0), x(T), \frac{d}{dt}x(0), \frac{d}{dt}x(T), \frac{d^2}{dt^2}x(0), \frac{d^2}{dt^2}x(T)$ にそれぞれ多項式を代入すれば、

$$\begin{cases} \alpha_0 &= x_o \\ \alpha_0 + \alpha_1 T + \alpha_2 T^2 + \alpha_3 T^3 + \alpha_4 T^4 + \alpha_5 T^5 &= x_f \\ \alpha_1 &= v_o \\ \alpha_1 + 2\alpha_2 T + 3\alpha_3 T^2 + 4\alpha_4 T^3 + 5\alpha_5 T^4 &= v_f \\ 2\alpha_2 &= a_o \\ 2\alpha_2 + 6\alpha_3 T + 12\alpha_4 T^2 + 20\alpha_5 T^3 &= \alpha_f \end{cases}$$

となる。この連立方程式を解けば、多項式係数が定まる。

連立方程式の求解

まず簡単に整理すると、

$$\begin{cases} \alpha_0 &= x_o \\ \alpha_1 &= v_o \\ \alpha_2 &= \frac{a_o}{2} \\ \alpha_3 + \alpha_4 + \alpha_5 &= x_f - x_o - v_o - \frac{a_o}{2} \\ 3\alpha_3 + 4\alpha_4 + 5\alpha_5 &= v_f - v_o - a_o \\ 6\alpha_3 + 12\alpha_4 + 20\alpha_5 &= a_f - a_o \end{cases}$$

と変形できる。ここで先ほど置いた前提 (終了時刻 $T=1$) を使っていることに注意。

下3つの連立方程式を解く必要があるが、面倒なので行列を使う。

$$\begin{bmatrix} 1 & 1 & 1 \\ 3 & 4 & 5 \\ 6 & 12 & 20 \end{bmatrix} \begin{bmatrix} \alpha_3 \\ \alpha_4 \\ \alpha_5 \end{bmatrix}= \begin{bmatrix} x_f - x_o - v_o - \frac{a_o}{2} \\ v_f - v_o - a_o \\ a_f - a_o \end{bmatrix}$$

逆行列を使うと、

$$\begin{bmatrix} \alpha_3 \\ \alpha_4 \\ \alpha_5 \end{bmatrix}= \begin{bmatrix} 1 & 1 & 1 \\ 3 & 4 & 5 \\ 6 & 12 & 20 \end{bmatrix}^{-1} \begin{bmatrix} x_f - x_o - v_o - \frac{a_o}{2} \\ v_f - v_o - a_o \\ a_f - a_o \end{bmatrix}$$

ここで3×3行列 $\boldsymbol{M}$ の逆行列 $\boldsymbol{M}^{-1}$ は以下のように計算できる。

$$\begin{align*} \boldsymbol{M} &= \begin{bmatrix} m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \\ m_{31} & m_{32} & m_{33} \\ \end{bmatrix} \\ \boldsymbol{M}^{-1} &= \frac{1}{|\boldsymbol{M}|} \tilde{\boldsymbol{M}} \end{align*}$$

ただし $|\boldsymbol{M}|, \tilde{\boldsymbol{M}}$ はそれぞれ

$$\begin{align*} |\boldsymbol{M}| &= m_{11}m_{22}m_{33} + m_{12}m_{23}m_{31} + m_{13}m_{21}m_{32} - m_{11}m_{23}m_{32} - m_{12}m_{21}m_{33} - m_{13}m_{22}m_{31} \\ \tilde{\boldsymbol{M}} &= \begin{bmatrix} m_{22}m_{33}-m_{23}m_{32} & -(m_{12}m_{33}-m_{13}m_{32}) & m_{12}m_{23}-m_{13}m_{22} \\ -(m_{21}m_{33}-m_{23}m_{31}) & m_{11}m_{33}-m_{13}m_{31} & -(m_{11}m_{23}-m_{13}m_{21}) \\ m_{21}m_{32}-m_{22}m_{31} & -(m_{12}m_{32}-m_{12}m_{31}) & m_{11}m_{22}-m_{12}m_{21} \end{bmatrix} \end{align*}$$

である。（定義を書いておいたが、実際に手計算をする必要はなく、Pythonや関数電卓の機能を使って逆行列を求めさせればよい。）

逆行列を計算すると、

$$\begin{bmatrix} 1 & 1 & 1 \\ 3 & 4 & 5 \\ 6 & 12 & 20 \end{bmatrix}^{-1} = \frac{1}{2} \begin{bmatrix} 20 & -8 & 1 \\ -30 & 14 & -2 \\ 12 & -6 & 1 \end{bmatrix} = \begin{bmatrix} 10 & -4 & 0.5 \\ -15 & 7 & -1 \\ 6 & -3 & 0.5 \end{bmatrix}$$

という結果が得られる。

すなわち、係数 $\alpha_3, \alpha_4, \alpha_5$ は

$$\begin{align*} \begin{bmatrix} \alpha_3 \\ \alpha_4 \\ \alpha_5 \end{bmatrix} &= \begin{bmatrix} 10 & -4 & 0.5 \\ -15 & 7 & -1 \\ 6 & -3 & 0.5 \end{bmatrix} \begin{bmatrix} x_f - x_o - v_o - \frac{a_o}{2} \\ v_f - v_o - a_o \\ a_f - a_o \end{bmatrix} \\ &= \begin{bmatrix} 10 (x_f - x_o - v_o - \frac{a_o}{2}) - 4 (v_f - v_o - a_o) + 0.5 (a_f - a_o) \\ -15 (x_f - x_o - v_o - \frac{a_o}{2}) + 7 (v_f - v_o - a_o) - (a_f - a_o) \\ 6 (x_f - x_o - v_o - \frac{a_o}{2}) - 3 (v_f - v_o - a_o) + 0.5 (a_f - a_o) \\ \end{bmatrix} \\ &= \begin{bmatrix} 10 (x_f - x_o) - 6 v_o - 4 v_f - 1.5 a_o + 0.5 a_f \\ -15 (x_f - x_o) + 8 v_o + 7 v_f + 1.5 a_o - a_f \\ 6 (x_f - x_o) - 3 v_o - 3 v_f - 0.5 a_o + 0.5 a_f \\ \end{bmatrix} \\ \end{align*}$$

と求められる。

連立方程式を解くと最終的に、

$$\begin{cases} \alpha_0 &= x_o \\ \alpha_1 &= v_o \\ \alpha_2 &= 0.5 a_o \\ \alpha_3 &= 10 (x_f - x_o) - 6 v_o - 4 v_f - 1.5 a_o + 0.5 a_f \\ \alpha_4 &= -15 (x_f - x_o) + 8 v_o + 7 v_f + 1.5 a_o - a_f \\ \alpha_5 &= 6 (x_f - x_o) - 3 v_o - 3 v_f - 0.5 a_o + 0.5 a_f \end{cases}$$

という解が得られる。これをもとの5次多項式へ代入して整理すると、躍度最小軌道は

$$\begin{align*} x(t) &= \alpha_0 + \alpha_1 t + \alpha_2 t^2 + \alpha_3 t^3 + \alpha_4 t^4 + \alpha_5 t^5 \\ &= x_o + (x_f - x_o) \cdot (6t^5 - 15t^4 + 10t^3) \\ & \quad - v_o \cdot (3t^5 - 8t^4 + 6t^3 - t) \\ & \quad - v_f \cdot (3t^5 - 7t^4 + 4t^3) \\ & \quad - 0.5 a_o \cdot (t^5 - 3t^4 + 3t^3 - t^2) \\ & \quad + 0.5 a_f \cdot (t^5 - 2t^4 + t^3) \\ \end{align*}$$

と求められる。

ここまで1次元空間の場合で導出したが、2次元や3次元の場合でも、

$$\begin{align*} x(t) &= x_o + (x_f - x_o) \cdot (6t^5 - 15t^4 + 10t^3) \\ & \quad - v_{xo} \cdot (3t^5 - 8t^4 + 6t^3 - t) \\ & \quad - v_{xf} \cdot (3t^5 - 7t^4 + 4t^3) \\ & \quad - 0.5 a_{xo} \cdot (t^5 - 3t^4 + 3t^3 - t^2) \\ & \quad + 0.5 a_{xf} \cdot (t^5 - 2t^4 + t^3) \\ y(t) &= y_o + (y_f - y_o) \cdot (6t^5 - 15t^4 + 10t^3) \\ & \quad - v_{yo} \cdot (3t^5 - 8t^4 + 6t^3 - t) \\ & \quad - v_{yf} \cdot (3t^5 - 7t^4 + 4t^3) \\ & \quad - 0.5 a_{yo} \cdot (t^5 - 3t^4 + 3t^3 - t^2) \\ & \quad + 0.5 a_{yf} \cdot (t^5 - 2t^4 + t^3) \\ z(t) &= z_o + (z_f - z_o) \cdot (6t^5 - 15t^4 + 10t^3) \\ & \quad - v_{zo} \cdot (3t^5 - 8t^4 + 6t^3 - t) \\ & \quad - v_{zf} \cdot (3t^5 - 7t^4 + 4t^3) \\ & \quad - 0.5 a_{zo} \cdot (t^5 - 3t^4 + 3t^3 - t^2) \\ & \quad + 0.5 a_{zf} \cdot (t^5 - 2t^4 + t^3) \\ \end{align*}$$

といった同様の式が導出される。単に $x$ を $y$ や $z$ に置き換えただけ。

以上が、任意の位置・速度・加速度をもつ躍度最小軌道の導出である。

躍度最小軌道の導出: 開始・終了時点で静止状態の場合

上述の結果から、記事冒頭で述べたイージング曲線の式を導出してみる。

開始・終了時点で静止状態ということは $v_o=v_f=a_o=a_f=0$ だから、これらを代入すると躍度最小軌道は

$$\begin{align*} x(t) &= x_o + (x_f - x_o) \cdot (6t^5 - 15t^4 + 10t^3) \end{align*}$$

となる。冒頭の式 $6t^5 - 15t^4 + 10t^3$ が出てきた。

この式をよくみてみると、多項式 $6t^5 - 15t^4 + 10t^3$ をイージング曲線とする線形補間(Lerp)になっていることがわかる。

状態空間表現による定式化

最後に、状態空間表現 (state space representation) を使った定式化を紹介する。

まずは状態空間表現の数式から見てみる。状態空間表現では、3つのベクトル型変数、目標状態 $\boldsymbol{u}$、出力状態 $\boldsymbol{z}$、内部状態 $\boldsymbol{s}$ を使って、いまこの瞬間の「状態」を表現する。そして何らかの行列 $\boldsymbol{A}$, $\boldsymbol{B}$, $\boldsymbol{C}$ を使って、これらの関係性を表す。

$$\begin{align*} \dot{\boldsymbol{s}} &= \boldsymbol{A}\boldsymbol{s} + \boldsymbol{B}\boldsymbol{u} \\ \boldsymbol{z} &= \boldsymbol{C}\boldsymbol{s} \end{align*}$$

ここで $\dot{\boldsymbol{s}}$ は $\boldsymbol{s}$ を時間微分したもの。

上述の状態空間表現は、もともと制御工学の分野で使われてきた考え方である。制御工学になじみがない方向けに簡単に説明すると、たとえば部屋の中にエアコンが設置されているのをイメージしてほしい。部屋の室温がなるべく一定値 $\boldsymbol{u}$ になるよう、気温センサのデータ $\boldsymbol{s}$ を見ながら、エアコンの送風パワー $\boldsymbol{z}$ を自動調整したい。こういった多くのリアルタイム制御の問題に、状態空間表現を使うことができる。

というわけで、状態空間表現に躍度最小軌道をあてはめた数式を考えることで、リアルタイム版の躍度最小軌道が導出できることになる。

躍度最小軌道を状態空間表現に落とし込むにあたって、まずは変数 $\boldsymbol{u}$, $\boldsymbol{z}$, $\boldsymbol{s}$ の具体的な中身を決める（ある程度は自由に決めてよい）。そして出力状態 $\boldsymbol{z}$ が躍度最小軌道になるよう、行列 $\boldsymbol{A}$, $\boldsymbol{B}$, $\boldsymbol{C}$ の中身を導出してやればよい。

(もうひとつ気に留めておいてほしいのは、上式の時間 $t$ が連続時間であるということ。連続時間系のままだとプログラムとして実装できないので、離散時間の状態空間表現へ変換する必要がある。離散化についてはあとで説明する。)

変数

まずは、目標状態 $\boldsymbol{u}$、出力状態 $\boldsymbol{z}$、内部状態 $\boldsymbol{s}$ の中身を決める。

目標状態 $\boldsymbol{u}$ は、最終的な位置 $x_f$、速度 $v_f$、加速度 $a_f$ とする。

$$\boldsymbol{u} = \begin{bmatrix} x_f \\ v_f \\ a_f \end{bmatrix}$$

出力状態 $\boldsymbol{z}$ は、位置 $x$ のみをキャラクターの見た目に反映させればよい、と考えることができる。要素がひとつしかないのでベクトルではなくスカラーになる。

$$z = x$$

内部状態 $\boldsymbol{s}$ は、位置・速度・加速度と設定することで定式化しやすくなる。 (ここは天下り的ですんません)

$$\boldsymbol{s} = \begin{bmatrix} x \\ \frac{dx}{dt} \\ \frac{d^2x}{dt^2} \\ \end{bmatrix}$$

ここまでで変数の中身が決まった。

状態モデル

次は状態空間表現の式 $\dot{\boldsymbol{s}} = \boldsymbol{A}\boldsymbol{s} + \boldsymbol{B}\boldsymbol{u}$ と $\boldsymbol{z} = \boldsymbol{C}\boldsymbol{s}$ に出てくる係数行列 $\boldsymbol{A}, \boldsymbol{B}, \boldsymbol{C}$ の中身を決める。ここに、先ほど導出した躍度最小軌道の式を入れ込んでいく。

状態空間表現のひとつめの式 $\dot{\boldsymbol{s}} = \boldsymbol{A}\boldsymbol{s} + \boldsymbol{B}\boldsymbol{u}$ は状態モデルと呼ばれる。ここに先ほど決めたベクトル変数の中身を代入すると以下のようになる。元の式の左辺にある $\dot{\boldsymbol{s}}$ は $\frac{d}{dt}\boldsymbol{s}$ なので、各要素を時間微分している。

$$\begin{bmatrix} \frac{dx}{dt} \\ \frac{d^2x}{dt^2} \\ \frac{d^3x}{dt^3} \end{bmatrix} = \boldsymbol{A} \begin{bmatrix} x \\ \frac{dx}{dt} \\ \frac{d^2x}{dt^2} \\ \end{bmatrix} + \boldsymbol{B} \begin{bmatrix} x_f \\ v_f \\ a_f \end{bmatrix}$$

この等式を満たすように行列 $\boldsymbol{A}, \boldsymbol{B}$ を設計する必要がある。

状態モデルの行列 A, B の導出

まずは簡単に書けるところからはじめてみる。

行列の方程式を連立方程式として見てみると、両辺に $\frac{dx}{dt}$ と $\frac{d^2x}{dt^2}$ があることに気付く。

これらを等号で結べば $\frac{dx}{dt}=\frac{dx}{dt}$ と $\frac{d^2x}{dt^2}=\frac{d^2x}{dt^2}$ という（当たり前すぎる）方程式が出てくるはずだ。そうなるように行列の各要素に値をあてはめれば、

$$\begin{bmatrix} \frac{dx}{dt} \\ \frac{d^2x}{dt^2} \\ \frac{d^3x}{dt^3} \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ A_{31} & A_{32} & A_{33} \end{bmatrix} \begin{bmatrix} x \\ \frac{dx}{dt} \\ \frac{d^2x}{dt^2} \\ \end{bmatrix} + \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ B_{31} & B_{32} & B_{33} \end{bmatrix} \begin{bmatrix} x_f \\ v_f \\ a_f \end{bmatrix}$$

となる。

残った未確定の係数 $A_{31}, A_{32}, A_{33}, B_{31}, B_{32}, B_{33}$ が現れる方程式を書き下してみる。

$$\frac{d^3x}{dt^3} = A_{31}x + A_{32}\frac{dx}{dt} + A_{33}\frac{d^2x}{dt^2} + B_{31}x_f + B_{32}v_f + B_{33}a_f$$

ここから $A_{31}, A_{32}, A_{33}, B_{31}, B_{32}, B_{33}$ を求める必要がある。そのために、この式の中にある躍度最小軌道 $x(t)$ がどのような式だったか思い出してみる。

躍度最小軌道 $x(t)$ は5次の多項式で表せるので、次のように書ける。

$$\begin{align*} x(t) &= \alpha_0 + \alpha_1 {\frac{t}{T}} + \alpha_2 {\left( \frac{t}{T} \right)}^2 + \alpha_3 {\left( \frac{t}{T} \right)}^3 + \alpha_4 {\left( \frac{t}{T} \right)}^4 + \alpha_5 {\left( \frac{t}{T} \right)}^5 \end{align*}$$

ただしここでは終了時刻 $T$ が $1$ ではなく任意の値がとれるよう、$t \rightarrow t/T$ とスケーリングした値に置き換えてある。

この躍度最小軌道 $x(t)$ の時間微分を考えると、次のように計算できる。

$$\begin{align*} \frac{d}{dt}x(t) &= \frac{\alpha_1}{T} + 2 \frac{\alpha_2}{T^2} t + 3 \frac{\alpha_3}{T^3} t^2 + 4 \frac{\alpha_4}{T^4} t^3 + 5 \frac{\alpha_5}{T^5} t^4 \\ \frac{d^2}{dt^2}x(t) &= 2 \frac{\alpha_2}{T^2} + 6 \frac{\alpha_3}{T^3} t + 12 \frac{\alpha_4}{T^4} t^2 + 20 \frac{\alpha_5}{T^5} t^3 \\ \frac{d^3}{dt^3}x(t) &= 6 \frac{\alpha_3}{T^3} + 24 \frac{\alpha_4}{T^4} t + 60 \frac{\alpha_5}{T^5} t^2 \end{align*}$$

今回は開始時の条件を与えているので $t=0$ の場合について考える。上の式にそれぞれ $t=0$ を代入すると第1項だけが残って、

$$\begin{align*} x(0) &= \alpha_0 \\ \frac{d}{dt}x(0) &= \frac{\alpha_1}{T} \\ \frac{d^2}{dt^2}x(0) &= 2 \frac{\alpha_2}{T^2} \\ \frac{d^3}{dt^3}x(0) &= 6 \frac{\alpha_3}{T^3} \end{align*}$$

と大幅に整理できる。

ここに多項式係数 $\alpha_0, \alpha_1, \alpha_2, \alpha_3$ の中身を代入すれば、

$$\begin{align*} x(0) &= x_o \\ \frac{d}{dt}x(0) &= \frac{v_o}{T} \\ \frac{d^2}{dt^2}x(0) &= \frac{a_o}{T^2} \\ \frac{d^3}{dt^3}x(0) &= \frac{60}{T^3} x_f - \frac{60}{T^3} x_o - \frac{36}{T^3} v_o - \frac{24}{T^3} v_f - \frac{9}{T^3} a_o + \frac{3}{T^3} a_f \end{align*}$$

となる。これらを整理してやれば、

$$\frac{d^3}{dt^3}x(0) = \underbrace{-\frac{60}{T^3}}_{A_{31}} x_o \underbrace{-\frac{36}{T^2}}_{A_{32}} \frac{d}{dt}x(0) \underbrace{-\frac{9}{T}}_{A_{33}} \frac{d^2}{dt^2}x(0) + \underbrace{\frac{60}{T^3}}_{B_{31}} x_f \underbrace{-\frac{24}{T^3}}_{B_{32}} v_f + \underbrace{\frac{3}{T^3}}_{B_{33}} a_f$$

として、残りの行列係数 $A_{31}, A_{32}, A_{33}, B_{31}, B_{32}, B_{33}$ が導ける。

最終的に状態モデルは次のように表せる。

$$\begin{bmatrix} \frac{dx}{dt} \\ \frac{d^2x}{dt^2} \\ \frac{d^3x}{dt^3} \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ -\frac{60}{T^3} & -\frac{36}{T^2} & -\frac{9}{T} \end{bmatrix} \begin{bmatrix} x \\ \frac{dx}{dt} \\ \frac{d^2x}{dt^2} \\ \end{bmatrix} + \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ \frac{60}{T^3} & -\frac{24}{T^3} & \frac{3}{T^3} \end{bmatrix} \begin{bmatrix} x_f \\ v_f \\ a_f \end{bmatrix}$$

観測モデル

状態空間表現のふたつめの式 $\boldsymbol{z} = \boldsymbol{C}\boldsymbol{s}$ は観測モデルと呼ばれる。今回のケースではとても単純に記述できる。観測モデルの式にあてはめているだけなので、方程式としては単に $x=x$ でしかない。

$$x = \begin{bmatrix} 1 & 0 & 0 \end{bmatrix} \begin{bmatrix} x \\ \frac{dx}{dt} \\ \frac{d^2x}{dt^2} \\ \end{bmatrix}$$

これで躍度最小軌道を状態空間表現に落とし込むことができた。

離散化

いままで導出してきた状態空間表現は、時刻 $t$ が連続な場合のモデルだった。しかし、コンピュータ上のプログラムとして実装する際は、描画フレームごとに区切られたような離散的な時刻を扱うことになる。したがって最後に、ここまでで得られた状態空間表現を離散化する必要がある。

ここまでの連続時刻での定式化をまとめて書き直してみる。

$$\begin{align*} \dot{\boldsymbol{s}} &= \boldsymbol{A}\boldsymbol{s} + \boldsymbol{B}\boldsymbol{u} \\ z &= \boldsymbol{C}\boldsymbol{s} \end{align*}$$

$$\boldsymbol{u} = \begin{bmatrix} x_f \\ v_f \\ a_f \end{bmatrix}, \quad z = x, \quad \boldsymbol{s} = \begin{bmatrix} x \\ \frac{dx}{dt} \\ \frac{d^2x}{dt^2} \\ \end{bmatrix}$$

$$\boldsymbol{A} = \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ -\frac{60}{T^3} & -\frac{36}{T^2} & -\frac{9}{T} \end{bmatrix}, \quad \boldsymbol{B} = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ \frac{60}{T^3} & -\frac{24}{T^3} & \frac{3}{T^3} \end{bmatrix}, \quad \boldsymbol{C} = \begin{bmatrix} 1 & 0 & 0 \end{bmatrix}$$

さて、上式に出てくるなかで実装するのにやっかいな変数が、内部状態の時間微分 $\dot{\boldsymbol{s}}$ である(逆に言えばそれ以外はそのまま実装できる)。そこで、微分を差分として近似することを考える(オイラー法)。

$$\dot{\boldsymbol{s}}(t) \approx \frac{\boldsymbol{s}(t+\Delta t) - \boldsymbol{s}(t)}{\Delta t}$$

ただし $\Delta t$ は離散時間の間隔(描画フレーム間隔など)である。

これを状態モデルの式に代入すると、

$$\begin{align*} \frac{\boldsymbol{s}(t+\Delta t) - \boldsymbol{s}(t)}{\Delta t} &= \boldsymbol{A}\boldsymbol{s}(t)+\boldsymbol{B}\boldsymbol{u}(t) \\ \therefore \boldsymbol{s}(t+\Delta t) &= \left( I + \Delta t\boldsymbol{A} \right) \boldsymbol{s}(t) + \Delta t \boldsymbol{B}\boldsymbol{u}(t) \end{align*}$$

という式が出てくる。行列を使わずに書き下せば、

$$\begin{cases} x_{i+1} &= x_i + \Delta t \cdot v_i \\ v_{i+1} &= v_i + \Delta t \cdot a_i \\ a_{i+1} &= a_i - \Delta t \cdot \left[ \frac{60}{T^3} x_i + \frac{36}{T^2} v_i + \frac{9}{T} a_i - \frac{60}{T^3} x_f + \frac{24}{T^3}v_f - \frac{3}{T^3} a_f \right] \\ \end{cases}$$

という結果が得られる。ただし $\boldsymbol{s}(t)=[x_i~v_i~a_i]^T, \boldsymbol{s}(t+\Delta t)=[x_{i+1}~v_{i+1}~a_{i+1}]^T$ として変数を書き換えている。

これで離散化することができた。実際に実装するときはこの式を使えばよい。この式は、今の内部状態 $\boldsymbol{s}(t)$ をもとに次の状態 $\boldsymbol{s}(t + \Delta t)$ へ更新する。ここで描画フレーム間隔(UnityでいうTime.deltaTime)を $\Delta t$ とすれば、この計算を毎フレーム回すことでリアルタイムに躍度最小軌道が得られることになる。

(本当はオイラー法よりもルンゲクッタ法を使った離散化のほうが正確なのだけれど、とりあえずこれで十分ということにしておく。)

Unityでのリアルタイム実装

ここまでで導出した状態空間バージョンの躍度最小軌道をUnityで実装する。躍度最小軌道のコアとなる部分は後述の MinJerkFollower.cs というスクリプトに実装した。せっかくなのでさらに応用して、簡単に3Dキャラクターモデルを動かすところまでやってみる。

今回参考にしたのは、jumius氏の講演動画「メタバースにいきものを創る」。このなかで、

手のターゲット位置を 200 ms おきに 400 ms かけて追従すると自然に見える

という例が紹介されていたので、これを試してみる。

https://www.youtube.com/watch?v=kpjchAf1bek

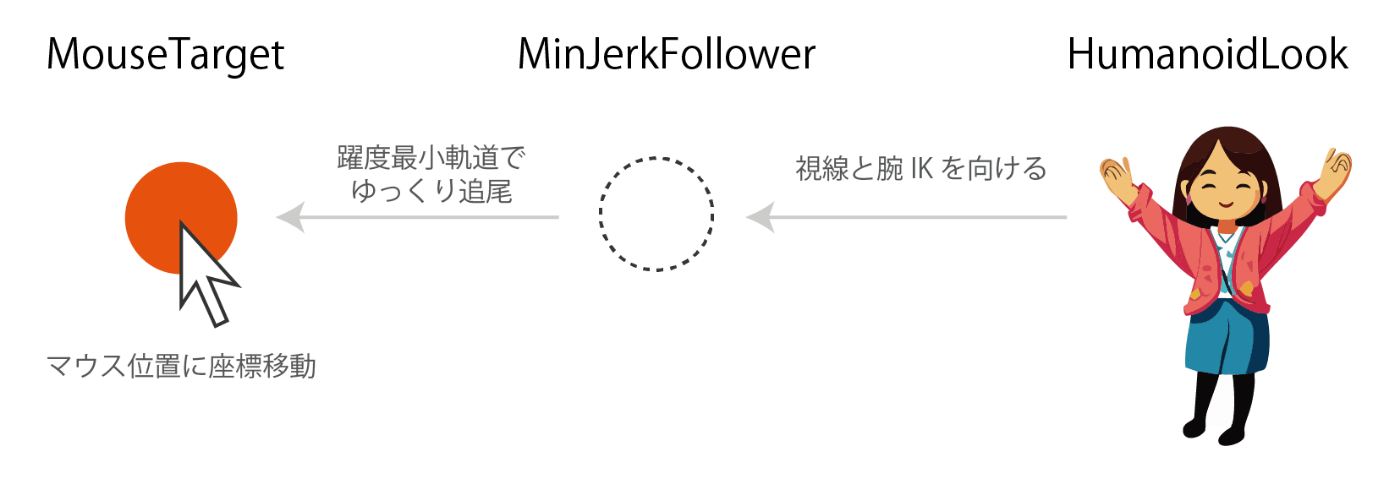
ここでは3つのスクリプトに分けて実装する。

• MouseTarget: ターゲットをマウス位置に移動する。
• MinJerkFollower: ターゲットを躍度最小軌道で追尾する。
• HumanoidLook: 3Dモデルの視線と腕を制御する。

MouseTarget.cs

ターゲット用のオブジェクトをゲーム画面のマウス位置に移動させるシンプルなスクリプト。
Sphereなどにアタッチしておくと見た目上わかりやすい。

// SPDX-License-Identifier: Unlicense
using UnityEngine;

public class MouseTarget : MonoBehaviour
{
    public Vector3 offset = new Vector3(0, 0, 1);

    void Update()
    {
        var screenPosition = Input.mousePosition + offset;
        transform.position = Camera.main.ScreenToWorldPoint(screenPosition);
    }
}

MinJerkFollower.cs

躍度最小軌道でターゲットオブジェクトを追尾するスクリプト。

ここまでで導出した「状態空間バージョンの躍度最小軌道」の式をそのまま実装すればよいが、今回の用途に合わせて少し条件を加えておく。ターゲットに到達した時点で静止してほしいので、終了速度 $v_f = 0$、終了加速度 $a_f = 0$ という条件を課すことにする。すると、以下のように少し簡略化される。

$$\begin{cases} x_{i+1} &= x_i + \Delta t \cdot v_i \\ v_{i+1} &= v_i + \Delta t \cdot a_i \\ a_{i+1} &= a_i - \Delta t \cdot \left[ \frac{60}{T^3} (x_i - x_f) + \frac{36}{T^2} v_i + \frac{9}{T} a_i \right] \\ \end{cases}$$

この数式を実装したのが以下のスクリプトである。これを空のGameObjectにアタッチしておく。

// SPDX-License-Identifier: Unlicense
using UnityEngine;

public class MinJerkFollower : MonoBehaviour
{
    public Transform target;  // 追尾したいオブジェクト
    public float followInterval = 0.2f;  // 200 ms 間隔
    public float followDuration = 0.4f;  // 400 ms かけて追従

    float intervalTime = 0;
    Vector3 targetPosition;
    Vector3 position;
    Vector3 velocity;
    Vector3 acceleration;

    void Start()
    {
        position = target.position;
        targetPosition = target.position;
    }

    void Update()
    {
        var dt = Time.deltaTime;
        intervalTime += dt / followInterval;
        if (intervalTime >= 1)
        {
            // intervalTimeごとにターゲット位置を更新
            targetPosition = target.position;
            intervalTime -= (int)intervalTime;
        }

        // 内部状態の更新
        var xf = targetPosition;
        var x = position;
        var v = velocity;
        var a = acceleration;
        var t = followDuration;
        var tt = followDuration * t;
        var ttt = followDuration * tt;
        position = x + dt * v;
        velocity = v + dt * a;
        acceleration = a - dt * (60 / ttt * (x - xf) + 36 / tt * v + 9 / t * a);

        // 出力
        transform.position = position;
    }
}

HumanoidLook.cs

キャラクターの「視線」と「手先」を制御するためのスクリプト。

視線と手先を動かすには IK (Inverse Kinematics) が必要になるが、ここではUnity標準のIK機能を使う。こだわりたい人は Final IK などを使ってもいいかもしれない。

// SPDX-License-Identifier: Unlicense
using UnityEngine;

public class HumanoidLook : MonoBehaviour
{
    public Transform target;  // MinJerkFollowerがアタッチされたGameObjectを指定する
    public Animator animator;
    [Range(0, 1)]
    public float weight = 0.2f;
    [Range(0, 1)]
    public float weightBody = 0.1f;
    [Range(0, 1)]
    public float weightHead = 0.6f;
    [Range(0, 1)]
    public float weightEyes = 0.5f;
    [Range(0, 1)]
    public float clamp = 0.5f;

    void OnAnimatorIK(int layerIndex)
    {
        // 視線を向ける
        animator.SetLookAtWeight(weight, weightBody, weightHead, weightEyes, clamp);
        animator.SetLookAtPosition(target.position);
        // 左手を指定位置に置く
        animator.SetIKPositionWeight(AvatarIKGoal.LeftHand, 1);
        animator.SetIKPosition(AvatarIKGoal.LeftHand, target.position);
    }
}

ここではサンプル3Dキャラクターとしてプロ生ちゃんの3Dモデルを使う。

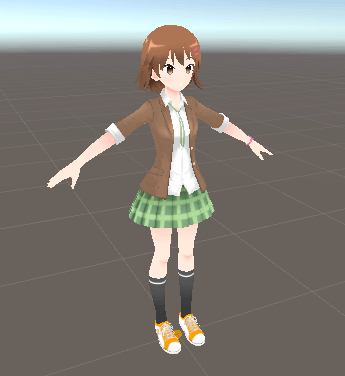
上で実装した HumanoidLook スクリプトは、必ずAnimatorがくっついているオブジェクトにアタッチする。Animator がくっついていないところにアタッチすると、実装した OnAnimatorIK() が呼び出されずIKが実行されないので注意。

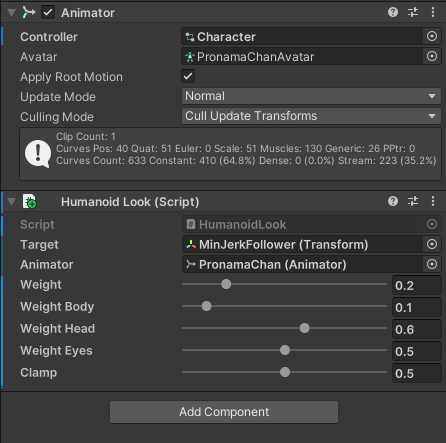
(1) プロ生ちゃんのAnimatorがついているところにHumanoidLookをアタッチする

さらに以下の設定をする。これもUnity標準のIK機能を使うために必要になる。

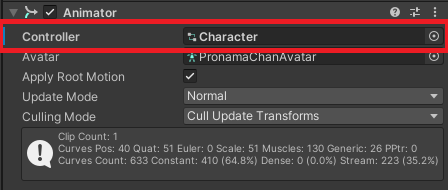
(2) プロ生ちゃんの Animator に適当な AnimationController を設定する

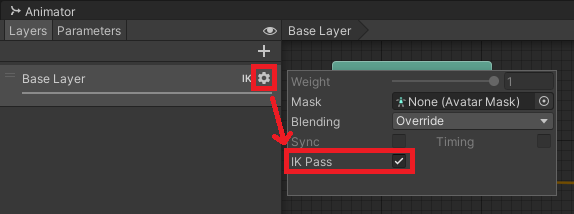
(3) 設定した AnimationController を開き、レイヤー設定の IK Pass にチェックを入れる

こうして完成したのがこちら。それっぽく追従する動作がリアルタイムに生成される。

躍度最小軌道で追従するプロ生ちゃん

もともと2点間の手先運動のモデルなので、ターゲットをパッパッと止めながら動かしたほうが自然に見える。ターゲットをグリグリ動かしたときは、手先が遅れて追従してしまう。もっと人間らしくするなら、動きの予測機構のようなものが必要になるかもしれない。

まとめ

• 躍度最小軌道は3Dキャラクター制御に向いている曲線
• 静止 → 静止 の場合はただのイージング曲線として実装できる
• 応用するとリアルタイムインタラクションにも使える

やってみた感想

躍度最小軌道はシンプルながら奥深いですね。当初に思っていたよりも底が深くてびっくりしました。

個人的には状態空間表現を使った方法がお気に入りです。状態空間表現にすることで、物理シミュレーションや他のモデルと融合させられそうな余地を感じます。さすがに躍度最小軌道だけだとインタラクションとしては物足りないので、ここからさらに拡張した動作生成モデルを構築してみたいです。

年末年始でこの記事を書いたのですが、文献を読み漁りつつ数学をやりつつ3DCGも触れて楽しかったです。

参考にした文献など

• Flash and Hogan (1985) : 元論文。サイトの「View Full Page PDF」から無料でダウンロードできる。詳しく書かれていて参考になる。
• 宇野 (2014) : 躍度最小軌道を含むさまざまな軌道モデルについて書かれている論文（オープンアクセス）。
• 田中『計算論的神経科学』(2019) : ヒトの動作を数式でモデル化する話が丸々一冊書いてある本。このあたりの話題に興味がある方にはたいへんおすすめ。躍度最小軌道については第2.2節に詳しい説明がある。
• A MINIMUM-JERK TRAJECTORY : 躍度最小軌道に関する細かい話がいろいろ載っていて便利。Shadmehr先生による講義資料の一部。状態空間による定式化についても書かれている。
• メタバースにいきものを創る (YouTube) : jumius氏による講演動画。