🎹
MIDIで歌声を再現する

2025/04/20に公開
正弦波の足し算でどんな周期波形でも表現できるという有名な話がありますよね。一方で、MIDI音源には正弦波の音色が搭載されています。ということは、任意の音をMIDI音源で近似して再生することが理論上可能なはずです。
この記事では、歌声をMIDIに変換する実験をしてみます。
Pythonで実装していきます。実際に動かしたい方は pip で以下のパッケージをインストールしておくとよいかもしれません。
pip3 install numpy matplotlib soundfile pyworld mido

 先人の試み音を正弦波で近似すること自体は、たとえばMP3やAACなどの圧縮フォーマットで使われているような一般的な考え方です。
ボーカルをMIDIで近似する実験は、ElekenさんやMSX研鑚推進委員会さんが昔から取り組まれています。Elekenさんの動画は中学生の頃に観て感動したのを覚えています。というわけでぜひともやりたい。
https://www.nicovideo.jp/watch/sm6280081

 その1: 所望の正弦波をMIDIで鳴らすにはまずはMIDIで正弦波を自由自在にコントロールすることが重要になってくるので、そのための方法を探っていきます。
ここでは先人たちと同様にMSGS音源を使うことにします。Windowsに標準搭載されているMIDI音源です。
今回の材料は、正弦波リードの音色である Program Change 081 (Bank 008/000) です。これで任意の正弦波を鳴らすには、振幅と周波数を調整するMIDIメッセージを送ればよさそうです。それぞれ次のMIDIイベントが対応しています。
振幅の制御: Expression (Control Change 011)
周波数の制御: ノート番号, ピッチベンド, ベンド幅

 振幅の制御: Expression音量を制御するMIDIイベントには CC 007: Volume と CC 011: Expression があります。どうやら固定値には Volume が、時々刻々と変化する調整には Expression が使われることが多いようです。
正弦波を鳴らしながら Expression の値を変えたとき、音声波形上でどのような振幅変化が起きるのか調べてみます。MIDIシーケンサの Domino で Expression を 0～127 の範囲で動かして再生しました。
録音したものがこちら。どうやら単純に線形な関係というわけではなく、ゆるいカーブがついているようです。
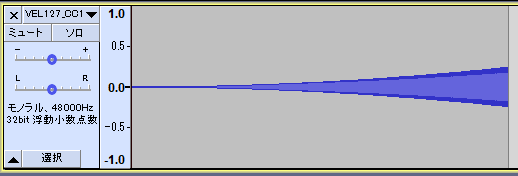
Pythonに取り込んで、これがどのようなカーブになっているのか調べてみます。いろいろな関数を試してみたところ、どうやら Expression を 0～1 に正規化して二乗した値 (x/127)^2 とおおむね対応するようです。
つまり、任意の振幅 a に設定したいときは Expression の値を 127\sqrt{a} に設定すればよいことがわかりました。

 周波数の制御: ノート番号, ピッチベンド, ベンド幅音の高さは、音符のノート番号で変えるのが一般的です。しかしこれだけだとドレミファソラシで表現できる音の高さに固定されてしまうので、ピッチベンドを併用して任意の周波数の音が再生できるようにします。
周波数 f Hz の音を鳴らしたいときの計算方法は、周波数とMIDIノート番号 のページに書かれています。
x = np.log2(f / 440.0) * 12 + 69
notenumber = int(np.round(x))
pb = int(np.round((x - n) * 8192 / bendrange))
周波数 f Hz の音を再生するには、音符のノート番号に notenumber を設定して、ピッチベンドの値 (-8192～8191) に pb を設定すればOKです。
ちなみにピッチベンドは、ベンドできる音程の範囲を何半音にするかという値 bendrange が設定できます。ここもうまく範囲設定をすれば、より正確に周波数 f Hz の音が鳴らせます。

 その2: 歌声を正弦波で近似するにはMIDIで正弦波を鳴らす方法がわかったので、次は歌声を正弦波のパラメータへ変換する方法を考えていきます。
とりあえず思いつくのは、音声信号を切り出しながら FFT (高速フーリエ変換) をかけて、振幅が大きい正弦波成分を見つけてくる方法です。



これでも実現可能ですが、いくつか問題があります。たとえば、切り出したフレーム間で周波数が急に変化しやすいのでピロピロした音になりやすかったり、同じような周波数の正弦波ばかりを拾ってしまったりします。
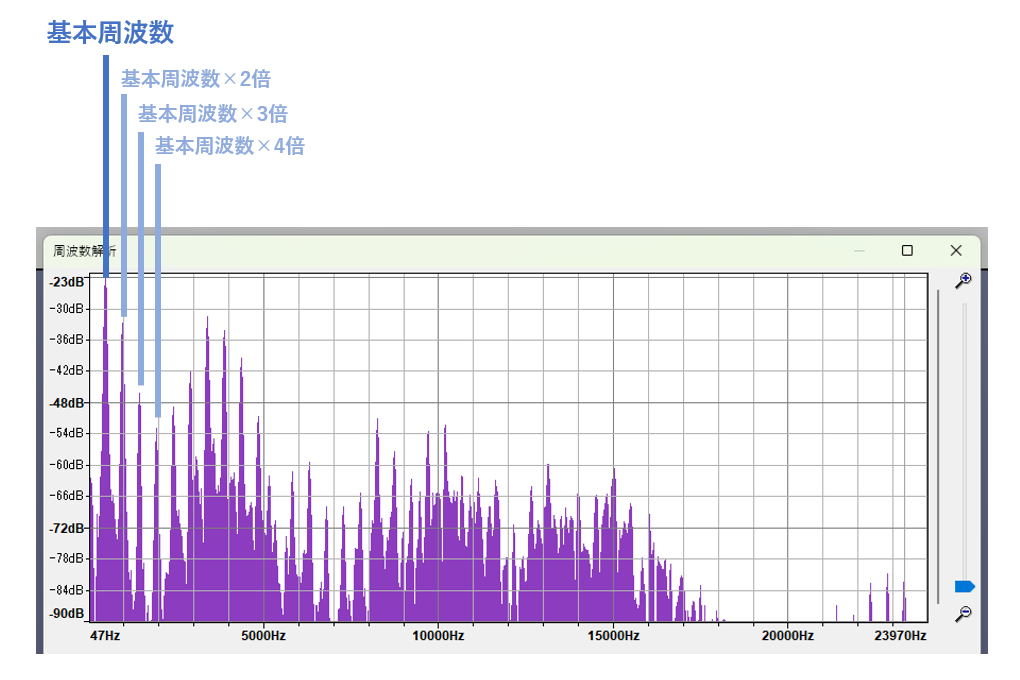
もっとうまくやるには、音声が整数倍音でできているという性質を活用します。はじめに音の高さを表す基本周波数 f_o Hz を調べておき、その整数倍の周波数における振幅値を求めます。たとえば4個の正弦波で近似する場合は f_o, 2f_o, 3f_o, 4f_o Hz の振幅を計算します。



この方式の良いところは、声の高さに応じてゆっくりと周波数が変化するようになるので、急な変化によってピロピロとした音になる現象が防げます。また、倍音だけを選ぶという制約が付いていることで、同じような周波数帯域ばかりを拾ってしまう問題も自然に解決できます。
ただし、基本周波数をうまく分析する必要があります。基本周波数の分析アルゴリズムを自力で組むのは大変なので、先人が開発した高性能なアルゴリズムを使うことにします。ここでは明治大学の森勢先生が開発された WORLD を使います。

 WORLDを使ってみるWORLDは人間の声に特化した音声分析合成システムです。音声信号からパラメータを分析し、さらにパラメータから音声信号を再合成できます。今回は再合成機能を使わず、分析部分のみを使っていきます。
まずは音声信号を読み込みます。ここでは童謡「うさぎ」を小春六花(Synthesizer V)に歌わせた usagi.wav を使いました。
import numpy as np
import matplotlib.pyplot as plt
import soundfile as sf

x, fs = sf.read("usagi.wav")

plt.figure(figsize=[12, 4])
plt.title("音声波形")
plt.plot(np.arange(len(x)) / fs, x)
plt.xlabel("時刻 [s]")
plt.ylabel("音圧")
plt.ylim(-0.5, 0.5)
plt.grid(True)
plt.show()
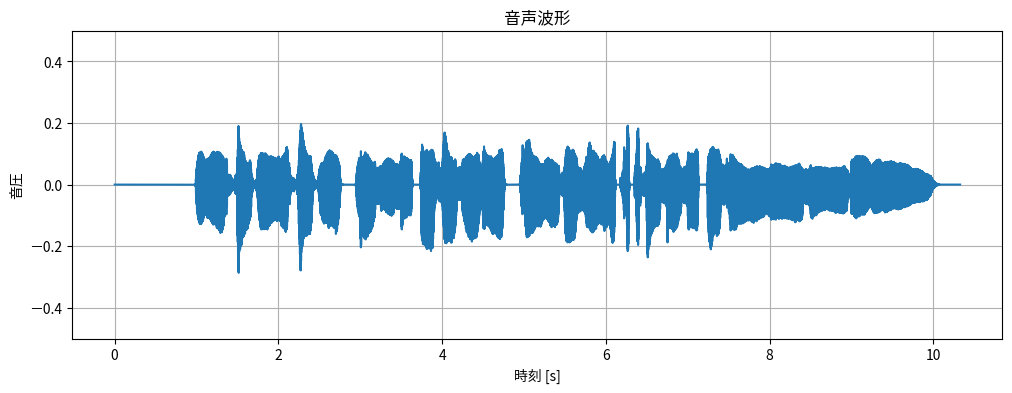
この音声信号をWORLDで分析をしてみます。WORLDに音声波形を入力すると、基本周波数(fo)、スペクトル包絡(sp)、非周期性指標(ap)の3種類のパラメータを分析してくれます。
import numpy as np
import matplotlib.pyplot as plt
import soundfile as sf
import pyworld as pw

x, fs = sf.read("usagi.wav")

period = 10.0  # 分析間隔[ms]
fo, time = pw.harvest(x, fs, frame_period=period)
sp = pw.cheaptrick(x, fo, time, fs)
ap = pw.d4c(x, fo, time, fs)

plt.figure(figsize=[12, 6])
plt.subplot(3, 1, 1)
plt.title("基本周波数")
plt.plot(time, fo)
plt.ylabel("周波数 [Hz]")
plt.xlim(0, time[-1])
plt.grid(True)
plt.subplot(3, 1, 2)
plt.title("スペクトル包絡")
plt.imshow(10 * np.log10(sp.T), origin="lower", aspect="auto", extent=[0, time[-1], 0, fs / 2 / 1000], vmin=-80, vmax=0)
plt.ylabel("周波数 [kHz]")
plt.subplot(3, 1, 3)
plt.title("非周期性指標")
plt.imshow(ap.T, origin="lower", aspect="auto", extent=[0, time[-1], 0, fs / 2 / 1000], vmin=0, vmax=1)
plt.xlabel("時刻 [s]")
plt.ylabel("周波数 [kHz]")
plt.tight_layout()
plt.show()
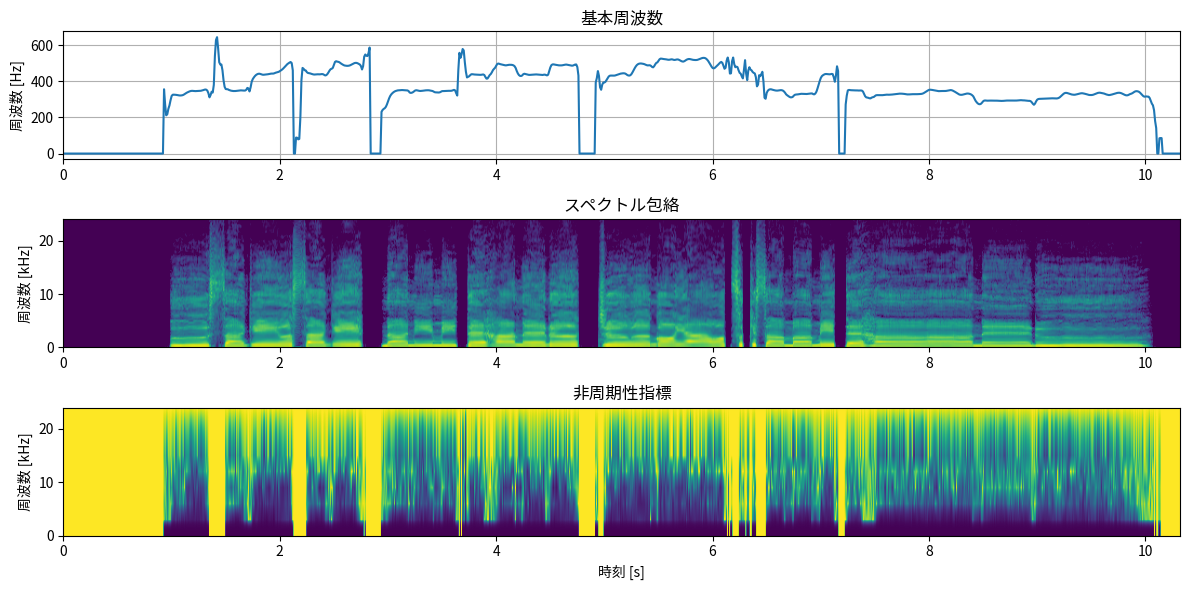
各パラメータの意味をざっくり載せておきます。

基本周波数: 声の高さ [Hz]

スペクトル包絡: 周波数ごとのおおまかなパワー(振幅の二乗)

非周期性指標: 周波数ごとのノイズの割合 [0.0-1.0]
ちなみに基本周波数が 0 Hz になっているところは、高さのある音声が検出されなかった区間です。

 WORLDパラメータを正弦波パラメータへ変換するWORLDで得られた基本周波数(fo)とスペクトル包絡(sp)を使って、正弦波の振幅と周波数を計算します。以下の図でいうオレンジ丸の座標が、各正弦波の振幅と周波数になります。
n_harmonics = 4  # 分析する倍音の個数
n_frames = len(time)  # 時間フレームの総数
fftsize = (sp.shape[1] - 1) * 2  # スペクトル包絡のFFT長

plt.figure()
for h in range(n_harmonics):  # 倍音ごと
    f = np.zeros(n_frames)
    a = np.zeros(n_frames)
    for frame in range(n_frames):  # 時間フレームごと
        # 倍音の周波数を計算
        f[frame] = (h + 1) * fo[frame]
        # 対応する周波数ビンを取得
        freqbin = int(np.round(f[frame] / fs * fftsize))
        # 指定した周波数におけるスペクトル包絡を取得
        power = sp[frame, freqbin] / np.sqrt(fftsize)
        # パワーを振幅へ変換
        a[frame] = np.sqrt(power)

    # プロット
    plt.subplot(2, 1, 1)
    plt.plot(time, f, label=f"正弦波{h + 1}")
    plt.subplot(2, 1, 2)
    plt.plot(time, a, label=f"正弦波{h + 1}")
plt.subplot(2, 1, 1)
plt.title("周波数")
plt.xlim(0, time[-1])
plt.grid(True)
plt.legend(loc="upper right")
plt.subplot(2, 1, 2)
plt.title("振幅")
plt.xlim(0, time[-1])
plt.grid(True)
plt.legend(loc="upper right")
plt.tight_layout()
plt.show()
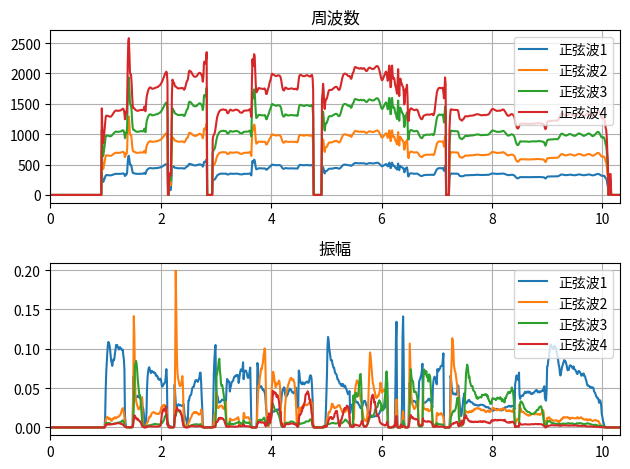
入力された歌声を、正弦波の情報（周波数と振幅）に変換することができました。

 NOTE: ノイズ成分は？音声信号には、ノイズ成分、たとえば「さ」の歯擦音 /s/ の音のようなものも含まれています。こうしたノイズ成分は扱わなくてもよいのでしょうか？
実は、ノイズ成分を省略してもそこそこ発話内容は聞き取れます。子音の聞き分けには、フォルマントの動きが重要な役割を果たしているという仮説（ローカス理論）があります。つまり正弦波成分だけで子音の聞き取りに必要な情報はある程度含まれているので、ノイズは必須ではないということです。
とはいえなんらかの方法でノイズ成分も再現すればより綺麗に合成できるようになるかもしれませんね。今回はそこまではやりませんが、工夫すると楽しそうです。

 MIDIで歌声を再現する「その1」のMIDIの正弦波制御と、「その2」の音声から正弦波を抽出を組み合わせます。

実装したものが以下です。（長いので省略しておきます）
wav2midi.pyimport numpy as np
import pyworld as pw
import soundfile as sf
import mido

# 設定
bpm = 120          # MIDIファイルのBPM
tpb = 480          # 1拍あたりのtick数
tick_interval = 8  # 時間変化のtick間隔
period = 10.0      # 分析間隔[ms]
n_harmonics = 7    # 正弦波の個数
fo_floor = 40      # 正弦波の最低周波数
track_vol = 127    # トラックボリューム
note_vel = 127     # ノートベロシティ

# MIDIファイルを作成
print("initializing midi data...")
mid = mido.MidiFile(ticks_per_beat=tpb)
tempo = mido.bpm2tempo(bpm)

# テンポ用トラックを追加
track = mido.MidiTrack()
messages = [
    mido.MetaMessage("set_tempo", tempo=mido.bpm2tempo(60), time=0),
    mido.MetaMessage("time_signature", numerator=1, denominator=8, time=0),
    mido.MetaMessage("set_tempo", tempo=tempo, time=240),
    mido.MetaMessage("time_signature", numerator=4, denominator=4, time=0),
]
track.extend(messages)
mid.tracks.append(track)

# 初期化用トラックを追加 (これがないと正弦波が鳴らない)
track = mido.MidiTrack()
messages = [
    mido.MetaMessage("track_name", name="System Setup", time=0),
    mido.Message("sysex", data=(126, 127, 9, 1), time=0),                      # GM System On
    mido.Message("sysex", data=(65, 16, 66, 18, 64, 0, 127, 0, 65), time=60),  # GS Reset
    mido.Message("sysex", data=(127, 127, 4, 1, 0, 127), time=0),              # Master Volume 127
]
track.extend(messages)
mid.tracks.append(track)

# 正弦波トラックを追加
sin_tracks = []
for h in range(n_harmonics):
    # 初期化
    track = mido.MidiTrack()
    messages = [
        mido.MetaMessage("text", text="CH Setup", time=188),
        mido.Message("control_change", channel=h, control=121, value=0, time=0),        # Reset All Control
        mido.Message("control_change", channel=h, control=0, value=8, time=1),          # CC 000 MSB = 008
        mido.Message("control_change", channel=h, control=32, value=0, time=0),         # CC 032 LSB = 000
        mido.Message("program_change", channel=h, program=80, time=0),                  # PC 081 Sine Wave
        mido.Message("control_change", channel=h, control=10, value=64, time=3),        # CC 010 Pan = 0
        mido.Message("control_change", channel=h, control=7, value=track_vol, time=1),  # CC 007 Volume
        mido.Message("control_change", channel=h, control=100, value=0, time=1),        # CC 100 RPN MSB = 0
        mido.Message("control_change", channel=h, control=101, value=0, time=0),        # CC 101 RPN LSB = 0
        mido.Message("control_change", channel=h, control=6, value=12, time=0),         # CC 006 BendRange = 12
        mido.Message("pitchwheel", channel=h, pitch=0, time=3),                         # PB = 0
        mido.Message("control_change", channel=h, control=11, value=0, time=43),        # CC 007 Expression = 0
    ]
    track.extend(messages)
    mid.tracks.append(track)
    sin_tracks.append(track)

# 音声ファイルを読み込む
print("reading audio file...")
x, fs = sf.read("usagi.wav")

# 基本周波数(fo)とスペクトル包絡(sp)をWORLDで分析
print("fo analysis...")
fo, time = pw.harvest(x, fs, frame_period=period, f0_floor=fo_floor)
print("sp analysis...")
sp = pw.cheaptrick(x, fo, time, fs)

# スペクトル包絡の振幅をスケーリング
n_frames = len(time)
fftsize = (sp.shape[1] - 1) * 2
sp_scaled = np.sqrt(sp)
sp_scaled /= np.max(sp_scaled)

# 正弦波トラック用のMIDIデータを作成
print("creating midi events...")
tick = 0
n_ticks = mido.second2tick(time[-1], tpb, tempo)
last_nn = [0] * n_harmonics
last_bendranges = [0] * n_harmonics
while tick < n_ticks:
    # フレーム位置
    frame = int(mido.tick2second(tick, tpb, tempo) / (period / 1000))

    # ノートの終了・開始 (初回または無声区間に入ったとき)
    if tick == 0 or fo[frame] <= fo_floor:
        # 発音終了 (現在のノート)
        frame_next = np.argmax(fo[frame:] > fo_floor)
        tick_next = mido.second2tick(frame_next * (period / 1000), tpb, tempo)
        if tick != 0:
            for h in range(n_harmonics):
                message = [
                    mido.Message("control_change", channel=h, control=11, value=0, time=tick_interval),
                    mido.Message("pitchwheel", channel=h, pitch=pb, time=0),
                    mido.Message("note_off", channel=h, note=last_nn[h], time=0),
                ]
                sin_tracks[h].extend(message)
        tick += tick_next

        # 次のノートがなかったら終了
        if tick_next == 0:
            break

        # フレーム位置を再計算
        frame = int(mido.tick2second(tick, tpb, tempo) / (period / 1000))

        # 発音開始 (次のノート)
        note_off_frame = frame + np.argmax(fo[frame:] <= fo_floor)
        note_fo = fo[frame:note_off_frame]
        pre_tick = max(tick_next - tick_interval, 0)
        for h in range(n_harmonics):
            # 次のノート区間内の基本周波数をもとに中心周波数とベンド幅を決める
            note_nn = np.log2((h + 1) * note_fo / 440.0) * 12 + 69
            max_nn = np.max(note_nn)
            min_nn = np.min(note_nn)
            center_nn = int(np.round((max_nn + min_nn) / 2))
            bendrange = int(np.ceil((max_nn - min_nn)))
            last_nn[h] = center_nn
            last_bendranges[h] = bendrange

            # イベントを追加
            messages = [
                mido.Message("control_change", channel=h, control=11, value=0, time=pre_tick),  # CC 007 Expression = 0
                mido.Message("control_change", channel=h, control=100, value=0, time=0),  # CC 100 RPN MSB = 0
                mido.Message("control_change", channel=h, control=101, value=0, time=0),  # CC 101 RPN LSB = 0
                mido.Message("control_change", channel=h, control=6, value=last_bendranges[h], time=0),   # CC 006 BendRange = 12
                mido.Message("note_on", channel=h, note=last_nn[h], velocity=note_vel, time=0),
            ]
            sin_tracks[h].extend(messages)
        continue

    if fo[frame] <= fo_floor:
        raise Exception(f"Error on tick {tick}, frame {frame}")

    # 音量と音程を調整
    for h in range(n_harmonics):
        # スペクトル包絡から正弦波の振幅を計算
        freqbin = int(np.round((h + 1) * fo[frame] / fs * fftsize))
        amp = sp_scaled[frame, freqbin]

        # Expression
        expression = int(np.sqrt(amp) * 127)

        # PitchBend (参考: https://www.geidai.ac.jp/~marui/matlab/node4.html)
        note_nn = np.log2((h + 1) * fo[frame] / 440.0) * 12 + 69
        pb = int(np.round((note_nn - last_nn[h]) * 8192 / last_bendranges[h]))

        # イベントを追加
        messages = [
            mido.Message("control_change", channel=h, control=11, value=expression, time=tick_interval),
            mido.Message("pitchwheel", channel=h, pitch=pb, time=0),
        ]
        sin_tracks[h].extend(messages)

    tick += tick_interval

# MIDIファイルへ書き出す
print("writing to midi file...")
mid.save("converted.mid")

print("done.")
このPythonコードを実行すると、usagi.wav を読み込んで converted.mid を作成します。
MIDIシーケンサで読み込んでみると、ちゃんと正弦波リードをコントロールチェンジで制御しているのがわかります。

このファイルを再生したのが以下の動画です。ちゃんと歌声になっていますね！

https://youtu.be/lxZT9CRdTlI

 おわりに昔からずっとやりたいと思っていた歌声の wav → midi 変換ができて嬉しいです。ソースコードも載せたので、試してみたいという殊勝な方(?)はぜひ遊んでみてください。