📑
ABC276の振り返り(A~F問題)
コンテストの振り返り
個人成績
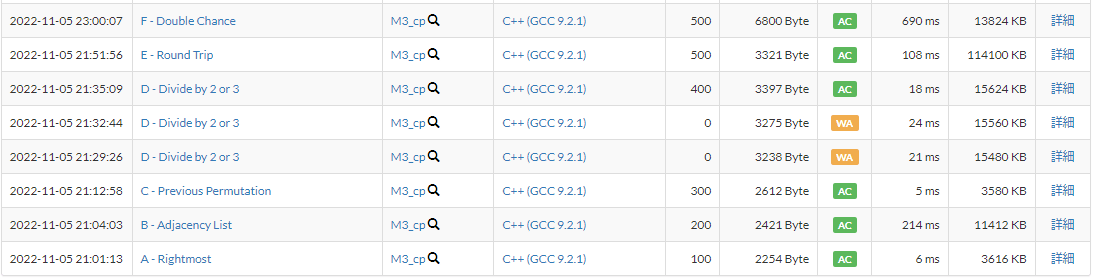
成績:5完2ペナ(51分56秒)
順位:1152位/7118人
パフォーマンス:1366
レート変化:1598→1577(-21)
パフォーマンスのボーダー
| 2400(理論値) | 2000 | 1600 | 1200 |
|---|---|---|---|
| 7完99:06 | 6完51:24 | 6完99:58 | 5完85:35 |
A~F問題の最速攻略時間
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 0:29 | 1:19 | 0:35 | 1:27 | 7:47 | 5:03 |
各問題の振り返り
A問題
最速との差:0分44秒(+0ペナ)
自分の解法
後ろから文字を見ていき、 a が出たらそこで探索を切る
上位・運営陣に見られた解法・実装
- 昇順に見ていって、
aがあれば更新
反省点
- 「昇順でもできる」といった発想が浮かばなかった
B問題
最速との差:1分31秒(+0ペナ)
自分の解法
愚直に実装した
vector<int> g[202020];
int n, m;
int main(){
cin >> n >> m;
REP(i, m){
int a, b;
cin >> a >> b;
g[a].emplace_back(b);
g[b].emplace_back(a);
}
REPS(v, n){
cout << SZ(g[v]);
sort(ALL(g[v]));
REP(i, SZ(g[v])){
cout << " " << g[v][i];
}
cout << endl;
}
}
上位・運営陣に見られた解法・実装
- 変わった実装は確認できなかった
反省点
- 実装スピードがやたらと遅い
C問題
最速との差:8分20秒(+0ペナ)
自分の解法
公式解説[1]と同じ実装をした
int n;
int p[101];
int main(){
cin >> n;
REP(i, n)cin >> p[i];
int idx = n - 1;
while(p[idx - 1] < p[idx])idx--;
idx--;
int less_idx = -1, less_max = -1;
for(int i = idx;i < n;i++){
if(p[idx] <= p[i])continue;
if(chmax(less_max, p[i])){
less_idx = i;
}
}
swap(p[idx], p[less_idx]);
sort(p + idx + 1, p + n);
reverse(p + idx + 1, p + n);
REP(i, n){
if(i)cout << " ";
cout << p[i];
}
cout << endl;
}
上位・運営陣に見られた解法・実装
-
prev_permutation()を利用した[2]
反省点
-
prev_permutation()を使う発想はあったのだが、テンパって採用しなかった- 後半の問題にどうしても時間がかかってしまうので、前半の時間を短くしようとすると、ついつい焦ってしまう
- swapをする部分でバグらせてしまった
D問題
最速との差:20分44秒(+2ペナ)
自分の解法
- 最終的にありうる
A_i - その値になるための最小回数を求める
int n;
int a[1010];
int cnt = 0;
map<int, bool> visited;
map<int, int> idx;
vector<int> g[505050];
vector<int> edge_list;
void make_vertex(int num){
if(visited[num])return;
visited[num] = true;
edge_list.emplace_back(num);
if(num % 2 == 0)make_vertex(num / 2);
if(num % 3 == 0)make_vertex(num / 3);
}
int calc(int num){
int ret = 0;
while(num % 3 == 0){
ret++;
num /= 3;
}
while(num % 2 == 0){
ret++;
num /= 2;
}
if(num != 1){
return -1;
}
return ret;
}
int main(){
cin >> n;
REP(i, n)cin >> a[i];
REP(i, n){
make_vertex(a[i]);
}
sort(ALL(edge_list));
int ans = HINF<int>();
REP(i, SZ(edge_list)){
int gl = edge_list[i];
int value = 0;
bool isok = true;
REP(j, n){
int cur = a[j];
if(cur < gl || cur % gl){
isok = false;
break;
}else{
int ret = calc(cur / gl);
if(ret == -1)isok = false;
value += ret;
}
}
if(isok)chmin(ans, value);
}
if(ans == HINF<int>()){
cout << -1 << endl;
}else{
cout << ans << endl;
}
}
上位・運営陣に見られた解法・実装
-
2^{x} \times 3^{y} \times z
反省点
- 問題を見た瞬間に「数字を頂点としてみれば、LCAで行けそう!」という発想をしてしまった
- 遷移が木ではないことにすぐ気づいたが、似たような考察に至ってしまった
E問題
最速との差:9分00秒(+0ペナ)
自分の解法
- 4方向にそれぞれDFSをして、閉路検出をした
int dx[4] = {1, 0, -1, 0}, dy[4] = {0, 1, 0, -1};
int h, w;
string fld[1010101];
vector<vector<bool>> visited;
bool dfs(int ci, int cj, int pi, int pj){
bool ret = false;
if(fld[ci][cj] == 'S')return true;
visited[ci][cj] = true;
REP(dir, 4){
int ni = ci + dy[dir];
int nj = cj + dx[dir];
if(pi == ni && pj == nj)continue;
if(!(0 <= ni && ni < h) || !(0 <= nj && nj < w))continue;
if(fld[ni][nj] == '#')continue;
if(visited[ni][nj])continue;
visited[ni][nj] = true;
ret |= dfs(ni, nj, ci, cj);
}
return ret;
}
int main(){
cin >> h >> w;
visited.resize(h, vector<bool>(w, false));
REP(i, h)cin >> fld[i];
int sr, sc;
REP(i, h)REP(j, w){
if(fld[i][j] == 'S'){
sr = i, sc = j;
}
}
REP(dir, 4){
int ny = sr + dy[dir];
int nx = sc + dx[dir];
if(!(0 <= ny && ny < h) || !(0 <= nx && nx < w))continue;
if(fld[ny][nx] == '#')continue;
REP(i, h)REP(j, w)visited[i][j] = false;
bool ret = dfs(ny, nx, sr, sc);
if(ret){
cout << "Yes" << endl;
return 0;
}
}
cout << "No" << endl;
}
上位・運営陣に見られた解法・実装
反省点
- 「閉路」という言葉とその検出方法を忘れてしまい、ググる時間が少々発生してしまった
F問題
※終了20分後に自力ACしました
最速との差:68分11秒(+0ペナ)
自分の解法
- 地道に期待値を求めた [6]
- (たぶん)「今見ている値より小さい値の数」「今見ている値より大きい値の総和」を求めるパートが本質で、ここは
2
- (たぶん)「今見ている値より小さい値の数」「今見ている値より大きい値の総和」を求めるパートが本質で、ここは
上位・運営陣に見られた解法・実装
- 分母の値はどこも同じなので、まとめて割る[7]
反省点
- 遷移と計算を冗長に書いてしまい、バグを処理するのにだいぶ時間をかけてしまった
- 「
X_i X_{i - 1} X
- 「
Discussion