$d$ の大きいところが局所的に存在する
- できるだけそういう箇所を回りつつ、全体を踏みたい
  - そもそも「 $d$ の大きいところの検出方法は？」
    - とりあえず、 $d \geq 100$ としておこう
公式のサンプル解から派生できないか
- 全体を最低1回踏む経路で、短いものが作れそう（短い方がスコアは高そう）
  - 全部到達しきった瞬間に最短でゴールを目指す

実際のルート構築に関して

大まかに移動する際に使えそうなものはあるか
- 右手法？
  - 未到達のマスが $1 \times k$ の形をしてしまったらどうしよう

「 $d$ の大きい塊」同士を行き来しながら、未到達点を潰す

到達済みのマスのコストを $10$ 、未到達マスのコストを $1$ としたダイクストラ
「 $d$ の大きい塊」内ではオイラーツアーをして必ず全頂点踏むようにする

2日目(12/2)

「『 $d$ の大きい塊』同士を行き来しながら、未到達点を潰す」を実装した。適宜到達済みマスのコストを上昇させるようにすることによって、全マス踏めるようにした。コストのパラメーターは考察の余地がありそう。

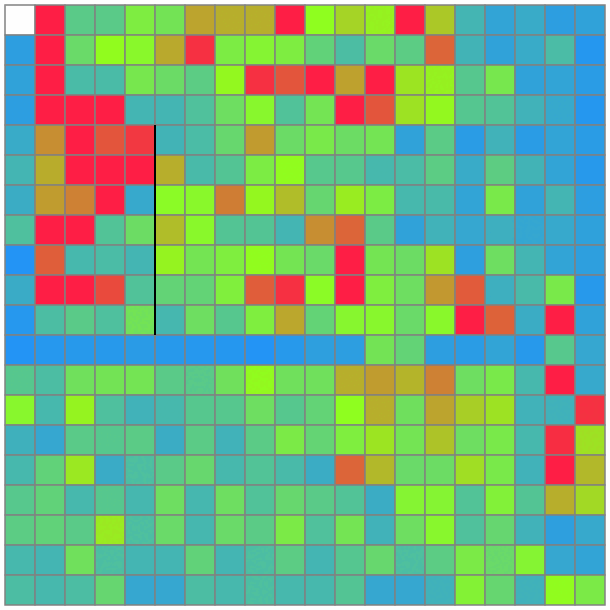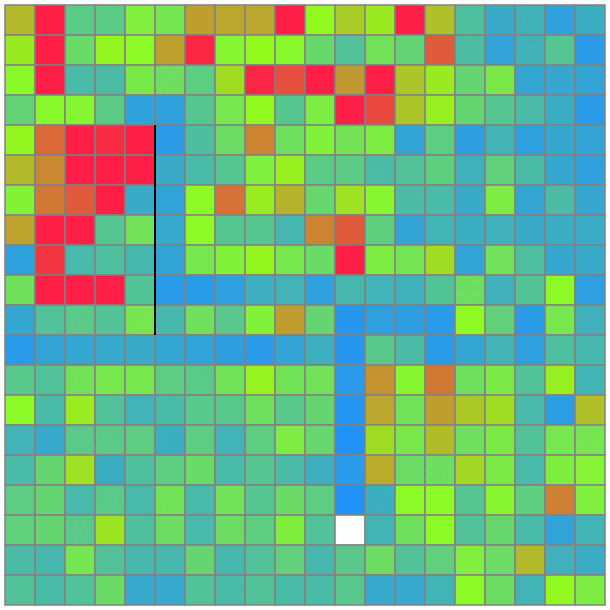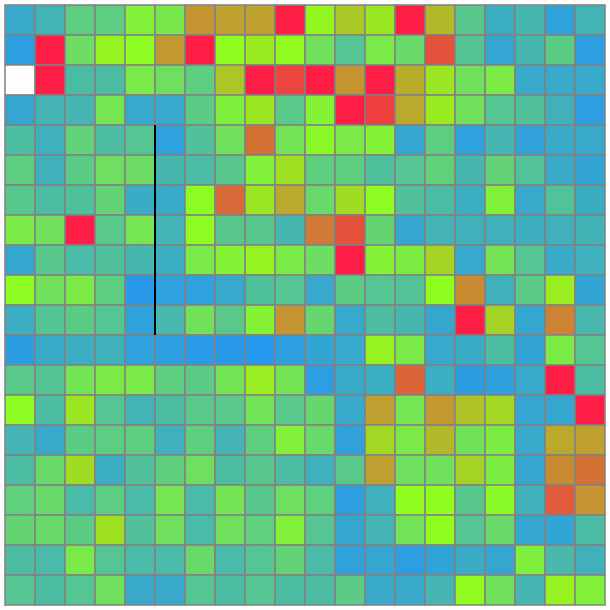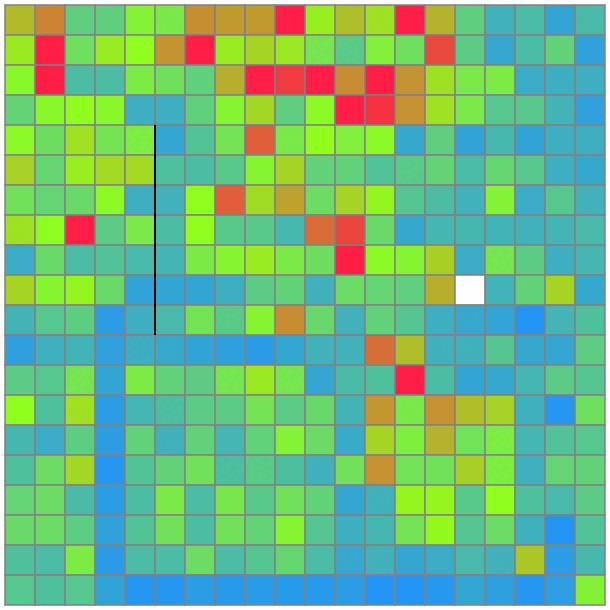
seed=0, score=3074479

通る回数が少ないマスは、いくら $d$ が小さくても $a$ が莫大になってしまう。

初期解が雑でも、何かいい方向に導いてくれることを信じて、雑焼きなましを書く。釣果ナシ。

3日目(12/3)

$L$ が比較的短い方針を考えてみる。「 $d$ の大きいところのみオイラーツアー」→「全体をオイラーツアー」をしてみると、案外スコアが高かった。

より汚れているところはより多い回数通過する
- 前回の到達から時間が経っているほうがいい
全体をできるだけ短い手数で回る

とよさそうなことに気づいた。全体を高々 $k$ 回以下で回りきる経路を構築するアルゴリズムを組もうと思ったが、難しすぎて断念。

手数を減らすことに、もっと注力してみる。TSPの近似解として、「もっとも近い未到達点を踏む」を繰り返すというものがあるらしいので実装してみる。

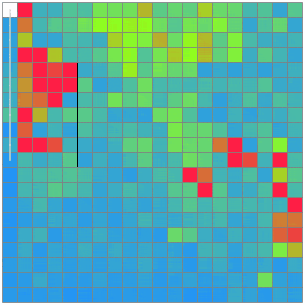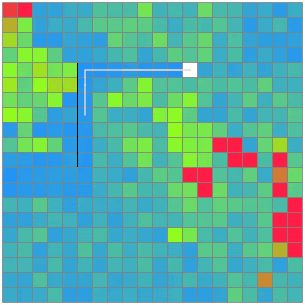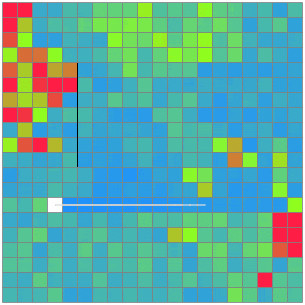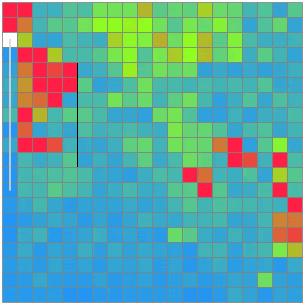
seed=0, score=2504932

提出。

提出結果

1位の6割程度だということが分かった。さらに経路を短くすることができるか→2-optを実装したものの、一切更新することが無くて困ってしまった。局所最適解すぎるようだ。

4日目(12/4)

さらに経路を短くすることができるか→2-optを実装したものの、一切更新することが無くて困ってしまった。局所最適解すぎるようだ。

諦めて別の方針を考える。壁がないものと仮定すると、「ループを作って、伸ばす」のがよさそうなのではないかと思った。 $d$ の大きいところを通過するときに、大回りしてから戻るようにすると、イイ感じに $2$ 回回れる気がした。

こんな感じの事を考えていた

長考の末、実装方法がわからず放置。

5日目(12/5)

経路を短くしたときのスコアの下限値を見積った。

void calc_minimum(){
    ll score = 0;
    rep(i, N)rep(j, N){
        score += N * N * D[i][j] / 2;
    }
    cout << score << endl;
}

曰く、提出した経路をいくら短くしても、ほぼ変わらないスコアだということが分かった。

前日に考えていたループの方針を考え直したが、やはりわからず。

この辺で進展がなくなってしまった。

どのような思考・実験をすればアイデアが尽きないのだろうか

本題でございます。参加記を基に、自分の取り組み方の反省点を探してみます。

ふわふわしすぎない

今回の問題における重要なポイントは、「 $d$ ごとに、どのような間隔で到達すればよいのかをいかに見極められるか」にあると思っています。何となく、「 $d$ が大きいところをたくさん通るのがよさそう」という発想は得られていたのですが、それ以上の吟味ができませんでした。

公式解説放送では、自由なマスに飛べるようルールを緩和して、解析的に求めていました。上位のプレイヤーは、緩和した問題を焼きなまして解いたり、作成した評価値を修正したりしながら解析的な解に近づいていました。

思いついた「 $d \geq 100$ 」といったルールも、実験を通してさまざまなアプローチを仕掛けていけば、 $d$ や $\sqrt{d}$ に比例することを導けたのかもしれません。

多面的にルールを緩和してみる

問題を難しくしている変数は大量に存在します。全部を一気に考えるのは難しいので、どれか $1$ つに絞って問題の理解度を深めるべきです。今回は「壁の有無」だけでなく、「ワープ可能」「 $N$ を小さくする」「 $d$ の分布をシンプルにしてみる」などの切り口があったはずです。

最初はもう少し単純な方法を考える

複雑な解法は実装が何回であり、（確証がつかめていないと）不安も大きいものとなってしまいます。問題が相変わらず難しい、というのもありますが、今回は初日にプログラムを書く手が一切動かないレベルでした。

とくに序盤は、着目する変数を減らしたり、非常にシンプルな解法を作って問題の理解度を深めるのが大切だと思います。

下手な焼きなましを避ける

経験上、AHC001（の延長戦）以外でうまい焼きなましをできた経験がなく、大半は山登り法を使っていました。うまい温度設計の心得を知らず、設計するのが難しいからです。そんな中、これまた適当なパラメーターで焼きなましをしようとしたのも、反省点です。

自分が捨てた方針を見直す

考えのまとめ

たとえば、1つの発想から1つだけが導き出されるのではなく、考えようによっては新たな方針を見つける基にもなるはずです（図の赤いところ）。

また、「到達点と未到達点で違うコストを振ったダイクストラ」という発想は、「 $d$ の閾値調整」や「新たな方針」でいい結果をもたらしてくれる可能性があります（図の青いところ）。

自分がコンテスト中に考えた物の中で、本当に諦めていいパターンは、「下界的に無理」という判断ができた「TSPの近似解」をベースにする発想くらいな気がします。

とにかく「実験ができるまでは、スコア上昇につながるエッセンスが眠っている」といったマインドで取り組むのが、僕には合っているのかもしれません。

焼きなましの近傍がデカすぎる

参加記には書かなかったのですが、解を作るたびに、それを初期解とした焼きなましをしようと挑戦していました。理想の形を思い描けず、「何か突然変異でも奇跡でもいいから、いい形を俺に見せてくれ」と言わんばかりに、雑な焼きなましをしていました。

作成した近傍

ランダム2点選択、最短経路の引き直し
- 「ダイクストラ法」も「採用したTSPの近似解」も、元々「最短経路」をベースに考えてるのだから、更新がほぼないのは当たり前かもしれない
ランダム2点選択、間に経由する点をランダムに追加・削除
- あまりにもランダムすぎる（当たればいいや精神がひどい）
  - 適当に作ると $L$ が大きくなってしまい、大きくスコアが悪化する
- 「元の経路長+2,4マス」程度にとどめておけば、望みがあったかもしれない

試行回数を増やしてもうまくいかなかったため、諦めてしまったのですが、よく考えれば、「近傍は小さい方がいい」ということを忘れていることに気づけた可能性もあります。いずれにせよ、もう少し焼きなましの研鑽を積むべきです。

まとめ

改めて、このようなまとめを書いてみると、「もう少しやれることがあったんだなぁ」という気持ちになりました。とくに、グラフ形式にして発想をまとめてみるのが自分にとって効果的でした。

さて、この記事の投稿日の翌日から、AHC029が始まります。スケジュール的に前半3日しかまともに参加できなさそうなのですが、早々に諦めることのないように、全力で取り組みたいと思います。

ここまで読んでいただきありがとうございました。

TL;DR

自己紹介

背景

AHC027上位解法まとめ

参加記

1日目(12/1)

解法のアプローチに関して