最新のテーブルデータ向けNNモデルをまとめてみた
はじめに
突然ですが、みなさんはテーブルデータの分類や回帰タスクを解くとき、どのようなモデルを使っていますか?
とりあえずCPUベースですぐに動かせて、それなりの精度が出せる、LightGBMなどの勾配ブースティング決定木(GBDT)モデルでまずは試してみるという方が多いのではないでしょうか。
実際、Kaggleなどの機械学習コンペティションにおいても、テーブルデータに対してはGBDTを試す、というのがここ十年近くの王道となっていたと思います。
一方で、ニューラルネット(NN)ベースのモデルとしては、決定木的な挙動とNNモデルを組み合わせたTabNetなどのモデルが有名でしたが、計算コストが高く、パラメータの緻密な調整が必要で、それでいてGBDTに匹敵する性能が出ない場合もある、といったデメリットがネックとなり、広く使われていたとは言い難い状況だったと思います。
かくいう私も、「テーブルデータといえばGBDT」が当たり前だと思っていた一人であり、テーブルデータ向けのNNモデルの最新動向についてはあまり追えていませんでした。
しかし、今年6月に公開された、テーブルデータ向けモデルのライブリーダーボードであるTabArenaを何気なく眺めたところ、上位に自分の全然知らないNNモデルが多く入っているのを発見して、衝撃を受けました。パラメータアンサンブルした場合の性能では、GBDTモデルを凌駕する精度のモデルも出てきています。

TabArenaリーダーボード : RealMLPやTabMといったNNモデルがGBDTモデルを上回っている。TabArenaサイトより引用。
これらのNNモデルの多くはCPUでも十分現実的な時間で学習が回るような高速化がなされていることも踏まえると、テーブルデータ分析において、最新NNモデルを理解して活用していくスキルはますます重要になってくると考えられます。
そこで、この機会に有望なNNモデルの論文を調査して、その仕組みをわかりやすくまとめてみることにしました。
本記事で扱うモデル
TabArenaのリーダーボードで上位に入っており、有望そうと考えた下記の4モデルを対象としています。完全に個人の主観ですが、論文の面白さ(≒難しさ)レベルについても付記しています。
- RealMLP:(★★★☆☆: シンプルなNNに様々な技術的工夫を追加しており、精度向上手法の勉強になる)
- TabM:(★★★★☆: 弱いサブモデルを内部的にアンサンブルさせるという、GBDTを連想させる手法。ほとんどの重みをサブモデル間で共有しても高い汎化性能が得られている)
- ModernNCA(★★★★☆: 近傍法という古典的な技術に、深層学習の最新知見を追加して強化。埋もれた技術を再発見することの重要性を学べる)
- TabPFN(★★★★★: 大量データでの事前学習を行い、個々のデータセットの推論時にはパラメータ更新が不要という、LLMに似た独創的なアプローチ)
GBDT系のモデルについては、既にとてもわかりやすい記事が多くありますので、本記事では解説しません。
RealMLP
論文
実装
どんなモデル?
RealMLPは、2024年に発表された、標準的な3層の多層パーセプトロン(MLP)に対して数多くの改良を加えることで、性能を大幅に向上させたモデルです。MLPは、Transformerなどの複雑なNNモデルに比べてパラメータ数が少なく、学習にかかる時間・コストが低い利点があります。こうした軽量なMLPを、様々な工夫によってGBDTに匹敵する精度に引き上げたのがRealMLPです。
また、大量のデータセットを用いたメタ学習を行うことで、個別のデータセットに依存しない優れたデフォルトパラメータを提供している点も大きな特徴です。このため、タスクごとにハイパーパラメータチューニングを行わずとも、安定した性能を得ることができます。
どこがポイント?
メタ学習による強力なデフォルトパラメータの算出
従来のNNモデルで安定した精度を出すためには、ハイパーパラメータの最適化(HPO)が不可欠でしたが、その実行に多大な時間・コストを要することが課題でした。 そこで著者らは、データセットに依存せず高い性能を示す「デフォルトパラメータ」を探索しました。
具体的には、118個のデータセットからなるメタ訓練ベンチマークを用いてハイパーパラメータやモデルアーキテクチャの最適化を行い、90個のデータセットからなるメタテストベンチマークでその性能を評価しました。
結果として、最適化されたデフォルトパラメータを用いたモデルは、HPOを行ったモデルの性能に匹敵することが分かりました。 これは、時間のかかるHPOを行わなくても、優れたデフォルトパラメータを利用するだけで非常に良い結果が得られることを示しています。
様々な工夫によるMLPの改良
RealMLPでは、前処理から学習のスケジューリング、アーキテクチャ、初期化方法など、様々な観点からのMLP改善手法が検証され、上述のメタ学習プロセスで有効だったものが採用されています。
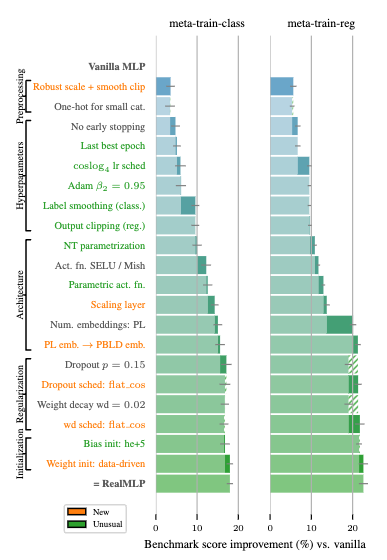
RealMLPで採用された工夫点とスコア改善幅: 分類タスク(左)、および、回帰タスク(右)について、様々な工夫によってメタトレーニングベンチマークスコアが改善していることが分かる。
このセクションでは、これらの工夫点のうち、特にスコアの改善幅が大きく重要と考えられる部分に絞って紹介します。
前処理:ロバストスケーリングおよびスムーズクリッピング
数値特徴量とone-hotエンコードされたカテゴリ特徴量には、ロバストスケーリングとそれに続くスムーズクリッピングが適用されます。
- ロバストスケーリングでは、データの中央部分(第一四分位点から第三四分位点)を利用してスケーリングを行います。 これにより、データの最小値・最大値を利用するMinMaxスケーリングに比べて、極端な外れ値によるデータ全体のスケールを歪みが抑制されます。
- スムーズクリッピングでは、スケーリングされたデータを、-3から3の範囲に滑らかに収めます。 これも、外れ値がモデルの学習結果に与える影響を過度に大きくしないための工夫です。
アーキテクチャ:スケーリング層の追加
ネットワークの最初の線形層の直前に、特徴量ごとに個別のスケーリング係数を乗算する層を追加しており、その係数も学習対象としています。 これにより、モデル自身が重要な特徴量を際立たせたり、不要な特徴量の影響を抑制したりと、「ソフトな特徴量選択」 が実現されています。
スケジューリング:
様々なデータセットに対して適切な探索と収束を促すために、周期的に変動するマルチサイクルの学習率スケジューラである
また、ドロップアウト率やWeight Decayといった正則化の強さについては、

各スケジューラーのプロット
(参考)異なるデータセットに対して、横断的なスコアをどうやって算出したの??
このセクションでは、メタ学習において、様々なデータセットをもとに、どのように横断的な総合スコアを算出したかを説明します。
まず、それぞれのデータセットにおける誤差を下記の方法で算出します。
- 分類タスクの場合: 分類誤差(1 - 正解率)、もしくは、(1 - ROC-AUC)
- 回帰タスクの場合: nRMSE (RMSEを目的変数の標準偏差で割った値)
これらの誤差について、下記の式で表されるシフト付き幾何平均誤差(Shifted Geometric Mean Error)を算出します。
ここでは、要するに、誤差の対数を取ったうえで平均を取り、再び指数変換して元のスケールに戻しています。対数を取ってから平均化することにより、例えば誤差が0.42→0.41に変化したときよりも0.02→0.01に変化したときの方が総合スコアの改善幅が大きく、より高く評価される ようになります。
制限はある?
欠損値への対応
RealMLPのメタ学習に用いられたデータセットでは、数値列に欠損値のある行はすべて事前に削除されています。 このため、数値的な欠損値を含むデータに対応しておらず、事前の欠損値処理が不可欠となります。
小規模/大規模データへの適用
チューニングおよび評価の対象となったデータセットは、1,000件から500,000件のデータセットに限られています。 そのため、データセットがこの範囲外の場合に、同じデフォルトパラメータが有効かは不明です。
総評は?
RealMLPは、NNモデルの中では軽量なMLPをベースに、包括的な性能改善検証を行い、GBDTに匹敵する精度を実現したモデルです。TabArenaのリーダーボードでも、様々なパラメータのモデルをアンサンブルした比較では、GBDTモデルを上回って、最も高い精度を示しています。
大量のデータセットを用いて最適化されたデフォルトパラメータが提供されているため、従来のNNモデルに比べて、個別のタスクに適用する際のハイパーパラメータチューニングの負担が大幅に軽減されるのは嬉しい点ですね。
数値の欠損値の前処理が必要という弱点はありますが、特に欠損値が少なくデータ数が1,000件以上ある場合には、試してみる価値が非常に高いモデルと言えるでしょう。
TabM
論文
実装
どんなモデル?
TabMは、2024年に発表された、標準的な多層パーセプトロン(MLP)を効率的にアンサンブルさせることで、高い性能を実現したモデルです。RealMLPのセクションでも紹介しましたが、MLPはTransformerなどの複雑なNNモデルに比べて、パラメータ数が少なく、学習にかかる時間・コストが低い利点があります。一方で構造が単純で表現力に劣るという課題がありますが、本手法はそれをアンサンブルによって解決し、GBDTにも匹敵する性能を達成しています。
通常のNNモデルのアンサンブルは、独立に複数のモデルを学習・推論させて結果を平均しますが、TabMで提唱されているアンサンブル手法では、ほとんどのモデルパラメータは共有され、一部のアダプタだけがサブモデルごとに異なる構成となっています。 この方法は、学習・推論の時間効率を改善するだけでなく、モデル全体への強い正則化として働き、汎化性能を向上させることが明らかにされています。
どこがポイント?
パラメータ効率のよいアンサンブル
ニューラルネットワークにおけるアンサンブルは、性能向上のための強力な手法ですが、同じモデルを複数独立して学習させる必要があり、時間・コストを大量に消費するという欠点がありました。
この問題を解決するため、アンサンブルを構成するサブモデル間でほとんどのパラメータを共有するBatch Ensembleという手法が2020年に提唱されています。具体的には、パラメータの大半を占める重み行列はサブモデル間で共有しており、「アダプタ」と呼ばれるサブモデル固有のパラメータを少数持っています。アダプタは、入力されるデータの調整(下図の
TabMは、この手法をMLPによるテーブルデータ分析に適用し、後述する初期化の工夫などを行うことで高い精度を実現しています。

TabMのアーキテクチャ: 入力を異なるk個の経路で処理したうえで、それらの平均値を予測値とすることで内部的にアンサンブルを実現している。最もパラメータ数が多い重み行列
こうした工夫により、TabMは内部的にアンサンブルを実現しつつも、NNモデルとしては高速な学習・推論速度を実現しています。 また、アンサンブルのないMLPに比べて、デッドニューロン(推論時に活性化せず予測に全く影響を与えないニューロン)の割合が半分近くまで減少し、パラメータを有効活用できていることも確認されています。

様々なデータセットに対する学習時間(左)/推論効率(右)の分布: TabMは、内部的にアンサンブルを行っているにもかかわらず、他のNNモデルに比べると高速な学習・推論を実現している。
また、興味深いことに、この重みの共有はパラメータ数を抑制するだけでなく、モデルの汎化性能を高める正則化の役割も果たしていることが分かりました。 パラメータを一切共有せず、サブモデルごとに独自の重みを持ったモデル(
観察に基づく初期化手法の調整
TabMの開発にあたっては、パラメータ効率化をさらに推し進めた

著者らは、この発見を元に、TabMの初期化方法に工夫を加えています。乗算されるアダプタ
これにより、学習の序盤は
弱い学習器のアンサンブルによる高い汎化性能
テーブルデータで安定した性能を示すGBDTでは、複数の決定木(弱い学習器)が内部的に構築され、それらの予測が集合的に組み合わされることで高い性能を発揮します。TabMにおいても、学習されるそれぞれのサブモデルは、むしろ単純なMLPよりも性能が低いことが確認されています。
様々なデータセットを用いた学習曲線の検証(下図)では、TabMのサブモデル自体は強い過学習の傾向を示しており、テストデータに対する予測性能は低いことが明らかになりました。 サブモデルの中で最も性能が良いモデルでも、その性能はたかだか単純なMLPと同程度でした。
しかし、こうしたサブモデルの予測値を平均したアンサンブル予測値では状況は一変して、過学習の傾向は抑制され、テストデータに対する予測精度は高くなります。 これは、個々のモデルが過学習気味であっても、その多様性によってデータのより多くの特徴を捉えることができ、集合的な予測は汎化能力が高く頑健なものになる、ということを示唆しています。

様々なデータセットに対する訓練中の損失の推移: 青がアンサンブルなしの単一MLPの損失、赤がサブモデルごとの個別予測値の損失の平均、緑が個別予測値を平均したアンサンブル予測値の損失。学習が左から右へ進むにつれて、赤は青よりも大きく上昇していて強く過学習している一方で、緑は過学習が抑制されていることが示唆される。つまり、TabMの個々のサブモデルは過学習していて弱いモデルだが、それらを平均したアンサンブル予測値は高い汎化能力を示す。
(参考)汎化性能として、現実世界でみられるデータドリフトへの対応力はどうなのか?
テーブルデータのベンチマークの多くでは、学習データとテストデータの分割はランダムに行われます。しかし、現実世界では学習に用いるデータと実際に推論するデータには時間的な差などがあり、データの分布に一定のシフト(分布シフト)が生じることが一般的です。
このため、ベンチマーク上で優れたモデルであっても、現実世界に適用した場合に十分な精度が得られないことが多くあります。本論文では、このような現実世界を考慮したデータ分割(ドメイン考慮分割)を行っているデータセットも用いて各モデルの評価を行っています。
その結果、ランダム分割のデータセットでは高い精度を出すNNモデルであっても、ドメイン考慮分割されたデータセットでは単純なMLPよりパフォーマンスが平均して劣る場合があることが分かりました。 一方で、TabMはこれらのデータセットにおいてもGBDTに匹敵する安定した性能を実現しており、より信頼性の高い手法であるといえます。
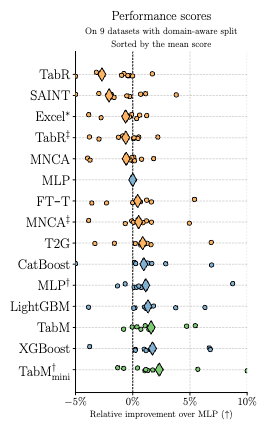
ドメイン考慮分割されたデータセットでの各モデルのパフォーマンス: ひし形で示された平均値に注目すると、オレンジ色で示された複雑なNNモデルはMLPと同等か、少し劣ったスコアとなっています。一方で、緑色で示されたTabM(および派生モデル)はMLPよりも優れており、GBDTに匹敵するスコアとなっています。
制限はある?
ハイパーパラメータチューニングの必要性
TabMの構築にあたっては、MLPアーキテクチャの構造(深さや隠れ層の次元数)もハイパーパラメータとして扱われ、データセットごとにチューニングされています。 様々なデータセットに対して汎用的なデフォルトパラメータの考察は行われていないため、高い精度を得るためには個別のチューニングが必要になる可能性があります。
また、TabMではアンサンブルを行うサブモデルの数(
論文中には、これらのハイパーパラメータ依存の精度変動について限定的な記載しかないため、ベースラインモデルとして、どんなデータセットに対してもデフォルトパラメータで安定した精度を実現できるかは未知数です。
総評は?
TabMは、単純なNNモデルであるMLPを、パラメータ効率的にアンサンブルさせることで、GBDTに匹敵する性能を実現したモデルです。ほとんどのパラメータをサブモデルで共有することが、むしろ正則化として働いてパフォーマンスを向上させるという興味深い結果も得られています。
TabMで提唱されたアンサンブル手法は、基本的にはアーキテクチャとは独立に適用可能です。そのため、より高性能なNNモデルが提唱されたとしても、本手法を適用することで、アンサンブルによる性能向上を比較的容易に実現できると考えられます。本記事で紹介したRealMLPのようなMLPの改善版モデルと組み合わせて使ってみるのも面白そうです。
TabMは、Kaggleの上位解法でもアンサンブルの一つとして採用されるなど、実績も伴ってきているため、ぜひ試してみて、パラメータの勘所を掴んでおくことをおすすめします。
ModernNCA
論文
実装
どんなモデル?
ModernNCAは、2024年に発表された、最近傍法をベースとしつつ、データの非線形変換にNNを用いたモデルです。2004年に提唱されたNCAという古典的な近傍法に対して、20年間で蓄積された深層学習に関する手法を適用することで、高い性能を実現しています。
また、近傍法における損失計算コストを抑制するため、確率的なサンプリングによる効率化を図っている点も特徴となっています。
どこがポイント?
古典的なNCAの現代化による性能向上
本論文では、まずは近傍成分分析(NCA)という古典的な手法の再検討を行うところからスタートしています。NCAとは、k近傍法(KNN)の予測精度を向上させるために2004年に提案された古典的手法です。
KNNでは、あるデータ点が与えられた際に、訓練データのうち距離が近いデータ点をk個抽出して、それらの目的変数の値から、与えられたデータ点の目的変数を予測します。しかし、KNNの性能はデータ点同士の「距離」の定義に大きく依存しており、タスクに適合した距離関数を設計することが性能向上の鍵でした。
そこでNCAでは、データ点に対して線形射影(線形変換)を行う行列を導入し、射影後の空間上で同じラベルを持つデータ点同士が引き寄せられ、異なるラベルを持つデータ点が引き離されるように、その行列を最適化します。この線形射影は、通常は元のデータ点の次元を削減するような変換を行い、タスクを解く上で重要な情報を保持しつつ、ノイズとなる情報を削減する役割を担っています。この手法により、データに合わせてカスタマイズされた距離関数(距離指標)が獲得できるため、KNNの精度向上に繋がるのです。
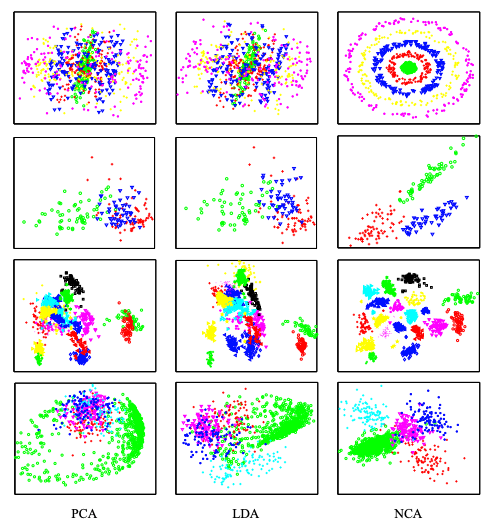
NCAによるデータ可視化結果: 右端がNCAによるデータ埋め込みの可視化。分類ラベルが色で表現されている。NCAでは、他手法と比較して、同じラベル同士が近づいて明確な分離がみられている。NCA提案論文より引用。
本手法では、まずこのNCAについて、下記の観点での改良を行い、L-NCAというモデルを構築しています。
- 次元削減制約を取り除き、高次元空間への射影も可能とするよう修正
- 最適化手法として、確率的勾配降下法(SGD)を適用
- 目的関数を、負の対数尤度の最小化として一般化
- 近傍のk個のみではなく、すべてのデータ点について距離で重み付けした予測を行うソフトNN手法を適用
このようなシンプルな改善を適用しただけで、精度は大きく改善して、NNモデルであるMLPを上回る性能が実現されました。この結果は、古典的な手法に対して、現代的な深層学習の技術を追加していくことで高い性能を得る、という著者らのアプローチが有望であることを示唆しています。
(参考)NCAの改良の詳しい流れは??
このセクションでは、NCAを改良してL-NCAに到達するまでに加えられた改良の詳細と、それぞれの性能への寄与を説明します。
まず、scikit-learn上のNCA実装に準拠したベースラインとなるモデルをNCAv0として、著者らはこのモデルに段階的な改善を加えて、性能変化を調べています。このベースラインの性能は、平均ランク4.400でした(ランクが小さいほど高性能)。
高次元への射影(NCAv1)
元々のNCAの実装では、線形射影は基本的に次元数を減らす(
確率的勾配降下法(SGD)の利用(NCAv2)
scikit-learnでのNCA実装では、L-BFGSという最適化手法が利用されています。これを、深層学習で広く用いられている確率的勾配降下法(SGD)に置き換えたところ、平均ランクは3.296とさらに改善しました。
L-BFGSは準ニュートン法の一種であり、安定した収束が得られる一方で、大規模データに不向きな場合があります。これをSGDに置き換えることで、訓練効率が向上し、最適化が促進されたと考えられます。
目的関数の更新(NCAv3)
本論文では、NCAを分類だけでなく回帰タスクにも適用するため、下記の一般化された式に従って、あるデータ
ここで、
最小化を目指す目的関数としては、下記の通り、予測値と正解の損失の総和として定義しています。
ここで、関数
予測戦略の改善(NCAv4 / L-NCA)
元のNCA実装では、学習時には上記のソフトな最近傍法を用いていましたが、予測時には「ハードな」KNN戦略(最近傍のデータ数個のみを用いた多数決)を適用していました。
本論文のNCAv4では、予測時にも学習時と同じソフトな最近傍法を適用して、全てのデータ点を距離に応じて重み付けした予測戦略をとるように修正しています。これによって平均ランクは2.962へと改善し、比較対象のMLP(平均ランク3.000)を上回る性能を達成しました。このモデルがL-NCAと呼ばれています。
NNを用いた非線形変換の導入による性能向上
L-NCAでは、データ点の変換には線形射影のみを利用していました。著者らは、この変換に非線形性を導入することでさらなる性能向上を実現した、ModernNCAを報告しています。ここでは、L-NCAの構成に、線形層、活性化関数、ドロップアウト層などからなる単層ニューラルネットワークのブロックを1つ以上追加することで、データ点の非線形的な変換を可能にしています。
また、入力のエンコーディングとして、数値特徴量に対してPLRエンコーディングという手法を適用しています。PLRエンコーディングは、周期的な埋め込み、線形層、活性化関数を介して、数値特徴量をNNモデルにとって扱いやすい高次元ベクトルに変換します。PLRエンコーディングによって性能が向上した理由として、こうした非線形性の埋め込みによって、ModernNCAの構造の単純性が補われているのではないかと著者らは考察しています。
このように、より柔軟な表現によってデータ点を高次元空間上に配置することにより大きな性能向上が見られ、ModernNCAは回帰タスクではCatBoostに次いで二番目のスコアを、分類タスクでは最高スコアを達成しています。
こうした高い性能にも関わらず、モデルサイズや訓練時間が比較的軽量なのもModernNCAの特徴です。ModernNCAと同様に近傍法をベースとしたTabRというNNモデルと比較すると、精度は同等レベルであるにも関わらず、訓練時間は大幅に短く、メモリ使用量も小さくなっています。
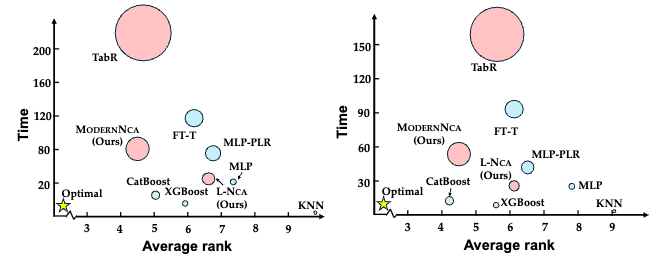
本論文で検証された各手法の性能と効率性の関係: 横軸が複数データセットでの平均順位、縦軸が平均トレーニング時間(秒)、円の大きさがモデルのメモリ使用量。左が分類タスク、右が回帰タスク。ModernNCAはいずれのタスクにおいても、高いパフォーマンスと効率性を両立している。
確率的サンプリングによる高速化と汎化
ModernNCAでは、損失関数の評価に際して訓練データ全体との距離を計算する必要があるため、学習時の計算負荷が非常に大きくなるという問題があります。
この問題を解決するために、本手法では確率的近傍サンプリング(SNS)という手法が提案されています。SNSでは、訓練データの一部が確率的に抽出されて、この一部の点との距離に基づいた損失計算が行われます。これは学習時にのみ適用され、実際の推論時においては、一部ではなく全ての学習データに基づいた近傍計算が行われます。
SNSを適用することで、学習効率が改善するだけではなく、モデルの汎化性能も向上することが実験的に確かめられています。これは、SNSのもつランダム性によって、実際の推論時に存在するノイズに対して堅牢なモデルが構築されるためと考えられます。
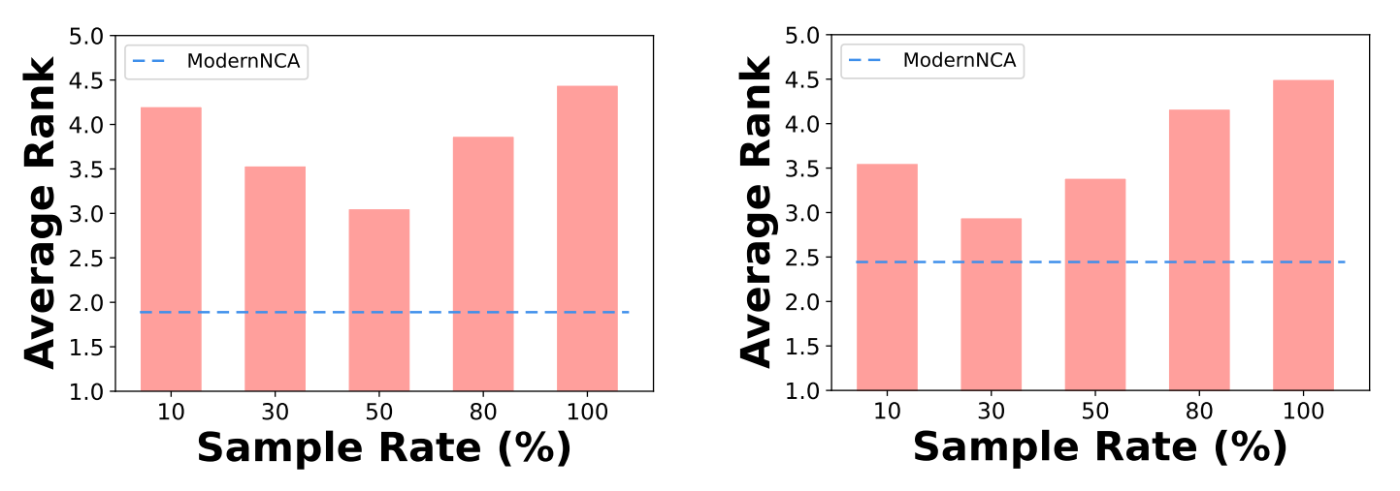
SNSでのサンプリング比率と性能の関係: 左が分類タスク、右が回帰タスク。サンプリングを行わない場合(サンプリング比率100%)よりも、一部をサンプリングする方が性能が高くなっている。
制限はある?
分布シフトへの対応
ModernNCAの根底にある考え方は、あるデータ点のラベルは、その近傍の訓練データのラベルをもとに予測できる、というものです。そのため、訓練データ分布に比べて、実際に処理するデータの分布がシフトしている場合には、訓練データでカバーされていない領域における予測精度が大きく損なわれるリスクがあります。
大規模データセットにおける推論速度制約
上で述べたように、ModernNCAの推論時には、全ての学習データとの距離を計算して予測を行います。そのため、訓練データが数百万行あるような大規模データの場合には、推論時に時間がかかる可能性があります。これは、学習を完了すれば高速に予測できるGBDTと比較した場合に潜在的な弱点となりえます。
総評は?
ModernNCAは、入力に線形射影を適用して近傍法を行う古典的なNCAという手法をベースに、近年の深層学習における技術を段階的に追加することで、GBDTに匹敵する性能を実現したモデルです。NCAに対して、SGDの導入や次元削減制約の除去などのシンプルな改善を行うだけで、MLPに匹敵する良好なパフォーマンスが実現されています。さらに、入力の距離空間への射影について、NNモデルを活用して非線形性を持たせることで、高い性能を達成しています。
また、ModernNCAは近傍法をベースとしているため、埋め込みを用いたデータ可視化についても良好な結果が期待できます。実際に論文中では、ModernNCAによる埋め込みを可視化することで、クラスごとに分離された構造化された変換ができていると報告されています。
学習方法の特殊さを加味すると、これまでに紹介したMLPベースの手法とは異なる観点からデータの特徴を捉えることが期待できるため、モデルアンサンブルを行うにあたってはぜひ加えておくべきモデルだと考えられます。
TabPFN
最初のバージョンの論文
v2の論文
実装
どんなモデル?
TabPFNは、Transformerをベースとしたアーキテクチャを持つモデルであり、合成された数百万〜1億以上のテーブルデータで事前学習されているという特徴があります。
すでに膨大なデータで事前学習されているため、個別のデータセットに適用する際は、一般的な機械学習モデルのように重みの更新は行いません。その代わりに、大規模言語モデル(LLM)でその有効性が示されたIn-Context Learning (ICL)という仕組みで、入力された訓練データの特徴をその場で読み取り、推論を行います。
このアプローチにより、特にデータセットのサイズが比較的小さい状況において、チューニング不要の高速な処理と、安定した高精度を両立できるのが最大の強みです。
2022年に発表された最初のバージョンでは、分類タスクにのみ対応し、扱えるデータ量も1000行/100列に制限されていました。その後、2025年に発表されたバージョン(v2)では、回帰タスクへの対応や扱えるデータ量の拡大(10000行/500列)などが行われ、その適用範囲が大きく広がりました。
どこがポイント?
In-Context Learningによる単一ステップでの学習・推論
TabPFNは、大量のデータで事前学習済みのモデルであり、新しいデータセットに対する学習と推論を、単一の順伝播で実行します。通常のモデルだと、新しいデータセットごとに重みの更新を行う場合が多いですが、TabPFNはすでに大量のデータセットでの事前学習が行われているため、新しいデータセットに対しても一度の推論で予測値を得ることができます。
新しいデータセットについて推論するときは、個々のデータ単位で処理するのではなく、訓練データとテストデータをまとめて一気に入力します。モデルは訓練データ全体を「お手本」として文脈内で学習し、テストデータに対する予測値を出力する、In-Context Learningという手法で推論します。この際にはパラメータの更新は行われないため、非常に高速な処理が可能です。
このあたりの挙動は、大規模言語モデル(LLM)と類似しています。LLMも、大量のデータでの事前学習を通じて汎用的な能力を獲得しており、実際の個別タスク実行時には推論のみを行います。また、タスク実行時にいくつかの具体例を与えたうえで推論させることで性能が向上する、In-Context Learningの能力を有していることが知られています。
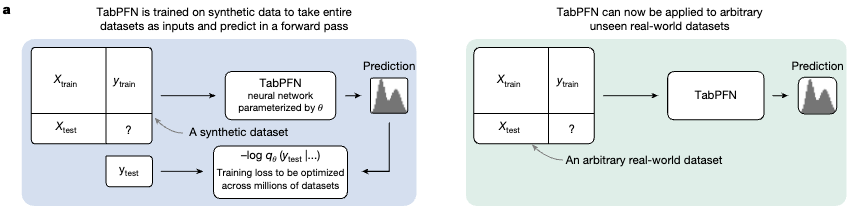
TabPFNの処理の流れ: 左図が事前学習、右図が新しいデータに対する推論を示す。事前学習では、データセット
大量の合成データセットによる学習
Transformerモデルを上記の方法で効果的に学習させるには、多様な関係性を持つ膨大なデータセットが必要です。現実世界のデータセットでは量が不足するため、本手法では大量の合成データセットのみを使って事前学習を行っています。
また、それらのデータセットは完全にランダムな内容ではなく、現実のテーブルデータと同様に、列間に何らかの構造的な関係性が存在している必要があります(完全にランダムなデータからは、法則性を見出して目的変数を予測することは不可能です)。
この要件を満たすため、TabPFNでは構造的因果モデル(SCM)と呼ばれる、ノード間の因果関係を表現するグラフ構造を基にデータセットを合成しています。具体的には、まずランダムなグラフ構造を生成し、そのグラフに初期ノイズを与えることで順に各ノードの値を計算します。そして、計算されたノードの中からいくつかのノードを特徴量
すなわち、あらかじめ「データを生み出す因果関係」を定義しておくことで、ランダム性を有しつつ、背後に特定のメカニズムが存在している、現実的なデータセットを作成することができるのです。
ただし、単一のSCMから多くのデータセットを作成して学習させただけでは、その特定のメカニズムにしか対応できない、汎化性能の低いモデルになってしまいます。そこでTabPFNでは、このSCMπ自体を確率的にサンプリングします。つまり、グラフの構造、各ノードの計算に用いられる関数、外生ノイズの分布などを毎回ランダムに決定し、その都度異なる「データを生み出す因果関係」を構築した上で、それを用いてデータセットを作成しているのです。
このような手法により、様々な変数間の関係パターンが含まれる、現実的なデータセットの集合を得ています。このグラフ構造のサンプリングが、初期のバージョンでは数百万回、v2ではなんと1億回以上も繰り返され、大量のデータセットが合成されました。

データ合成の流れ: (a)まず、ノードの数やグラフ形状、特徴量の数といったパラメータがサンプリングされる。(b)それに沿ってグラフ構造が構築され、初期ノイズを伝播させて値を計算したうえで、特徴量およびターゲットに相当するノードが選定される。それぞれのエッジには、下部に記載されているような様々な計算マッピングが割り振られている。(c)bを繰り返すことで、様々な特徴量-ターゲット間の関係性を表す多様なデータセットが生成される。
このように、極めて多様なグラフ構造に基づくデータセットを合成して、それを用いた学習を行うことで、TabPFNは強力な汎化性能を獲得します。新しいデータセットが与えられた際に、その背後にあるデータ生成メカニズムを踏まえた推論を行うため、様々なデータセットに対して妥当な予測を行うことができるのです。
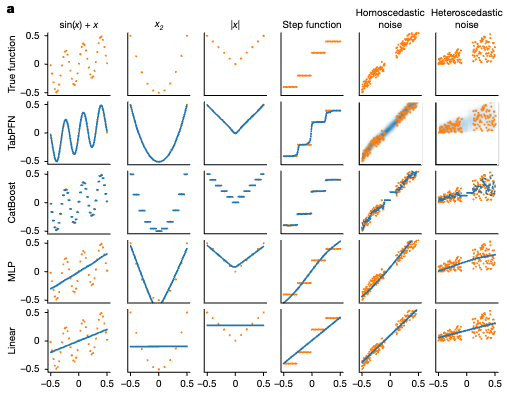
様々な形状の関数の予測結果: オレンジが実際の関数、青がモデリングされた関数。TabPFNは、様々な関数を精度良くモデリングできている。ニューラルネットであるにもかかわらず、ステップ関数もうまく近似できている。
(参考)なぜ、様々なデータセットで学習すると、メカニズムを踏まえた推論が実現されるの??
上記の説明ではサラッと書きましたが、「なぜ、様々なデータセットを用いて学習すると、メカニズムを踏まえた推論ができるようになるのか」と疑問に思った方もいるかもしれません。このセクションでは、TabPFNのアプローチがうまくいく理論的な裏付けを、なるべく分かりやすく解説します。
事後予測分布(PPD)の定式化
TabPFNは、PFN(事前データ適合ネットワーク)という、ベイズ推論を基盤としたフレームワークを採用しています。
ベイズ推論とは、観測されたデータ(証拠)を基に、事前に持っていた仮説を更新し、より確からしい推定(事後分布)を得るための統計的な枠組みです。
教師あり学習にベイズ推論を適用する場合、そのゴールは、訓練データセット
このPPDは、下記の式で表すことができます。ここで、
この式が成り立つことは、「事後予測分布(PPD)とは、存在しうるあらゆる仮説
この式は、ベイズの定理より
PPDを近似する関数の学習
この複雑な積分計算を直接行うのは非常に高コストであるため、PFNではTransformerモデルを用いて、入力
ということで、この近似関数をどのように学習すればよいか考えます。近似関数
ここで、KLダイバージェンスの定義は
第一項
この右辺の期待値は、実際にはモンテカルロ法によって近似されます。モンテカルロ法の適用のために、「データセットの事前分布
ここで、データセットの分布
-
仮説のサンプリング: まず、仮説の事前分布
p(\phi) \phi -
データのサンプリング: 次に、そのサンプリングされた仮説
\phi p(D|\phi) D
この2段階の生成プロセスこそが、TabPFNの事前学習で「一つの合成データセットを作る」手順そのものです。この生成されたデータセットから、さらにランダムにテストポイント
この操作を、十分多く繰り返しながら
新しいデータセットが与えられた際に、その背後にあるであろう様々なデータ生成メカニズムを想定し、それらの尤もらしさで重み付けを行った上でアンサンブル予測を行う――こうしたベイズ的な推論結果をTransformerを用いて学習したTabPFNは、多様なデータに対して妥当な予測を行うことができるのです。
(参考)事前学習の詳細はどうなってるの??
このセクションでは、TabPFNの事前学習が具体的にどのように行われるかを解説します。
事前学習の目的は、任意のデータセットが与えられたときに、その背後にある真の事後予測分布(PPD)を近似できるような、汎用的な推論モデルを構築することです。
-
合成データセットの作成
まず、一つのSCMを確率的にサンプリングします。ここでは、SCMのグラフ構造、各ノードの計算関数、外生ノイズの分布、そしてどのノードが特徴量Xでどれがターゲットyかという指定までを全て含んだ、「データ生成器」が得られます。この生成器は、外部からノイズの具体的な値(ランダムシード)さえ与えられれば、決定論的にデータの1行を計算できます。
この生成器に、ランダムシードを与えてデータを生成するプロセスを繰り返し、一つのSCMから一つのデータセット(v1では固定長で1024行、v2では最大2048行の範囲でランダム)を合成します。 -
データセットの分割と訓練
次に、この合成データセットを訓練用とテスト用に分割し、12層のTransformerアーキテクチャを持つニューラルネットワークに入力します。ネットワークは、訓練データ(X_{train}, y_{train} X_{test} -
反復
以上の処理を、v1では512個のデータセットを1バッチとして18000ステップ、v2では64個のデータセットで約200万ステップ繰り返します。
テーブルデータに適したAttentionアーキテクチャ
TabPFNは、標準的なTransformerのアーキテクチャをテーブルデータに最適化しています。その核となるのが2方向アテンションです。通常のTransformerのアテンション機構は1次元のシーケンスを処理しますが、TabPFNのアテンション機構では、入力されたテーブルの各セルを独立したトークンのように扱い、2つの異なる方向から情報集約を連続して行います。
1. 特徴量アテンション(横方向): 各サンプル内で、異なる特徴量同士がどのように関連しているかに注目します。
2. サンプルアテンション(縦方向): 各特徴量について、異なるサンプル間で値がどのように分布しているかに注目します。
この2方向のアテンション機構により、モデルはテーブル全体の構造的情報を効率的に捉えることができ、サンプルの順序や特徴量の順序に影響されない、より頑健な予測が可能になります。

TabPFNのアーキテクチャ: オレンジ色で示されたテストデータの予測を行う際には、横方向および縦方向のアテンションが計算され、表全体の情報を踏まえた予測が行われる。
制限はある?
データ量の壁
TabPFN v2では、効率的に扱えるデータは、サンプル数が10,000件、特徴量数が500個、クラス数が10個程度までに制限されています。この主な要因は、TabPFNが入力データセット全体をTransformerに入力して結果を得るため、サンプル数の2乗に比例して計算量やメモリ使用量が増大するためです。
この課題の解決策として、より長大なデータに対しても効率的に動作するTransformerアーキテクチャ(例: Longformer)の採用が、著者らによって今後の方向性として示唆されています。
苦手なデータ特性
TabPFNの学習データにはカテゴリ特徴量や欠損値も含まれますが、その生成パターンは現実世界の多様性を完全にはカバーしきれておらず、特に数値中心のデータで性能が最大化されるように設計されています。そのため、カテゴリ特徴量や欠損値が非常に多いデータについては、適用は可能ですが性能が悪化する傾向が報告されています。また、目的変数に無関係な特徴量が多く含まれる場合も同様に性能が劣化することが指摘されています。
この課題の解決策としては、事前分布の改良によってさらにデータセットの多様性を高めることが重要です。現状のデータセット生成においても、数値変数のカテゴリ変数化やランダムな欠損値の追加といった後処理は行われていますが、現実世界に存在するより複雑なパターン(例えば、欠損値の偏った発生メカニズムなど)を事前分布に組み込むことで、さらなる性能向上が期待されます。
総評は?
TabPFNは、In-Context Learningによってデータセット全体に対して一度の順伝播で学習・予測を行う、新しいアプローチのモデルです。事前学習の段階で、極めて大量かつ多様な因果グラフ構造を基にデータセットを合成・学習することで、高い汎化性能を達成しています。
新しいデータへの適用において勾配更新が不要であり高速に動作する点と、ハイパーパラメータチューニングなしで高い性能を達成できる点を踏まえれば、特にデータセットのサイズがそれほど大きくない状況においては、最初の選択肢として非常に有力な手法と言えるでしょう。
実際に、TabArenaのリーダーボードでも、TabPFNが対応可能なサイズのデータセットに絞った検証では、多くの既存手法を凌駕する高い性能を示しています。
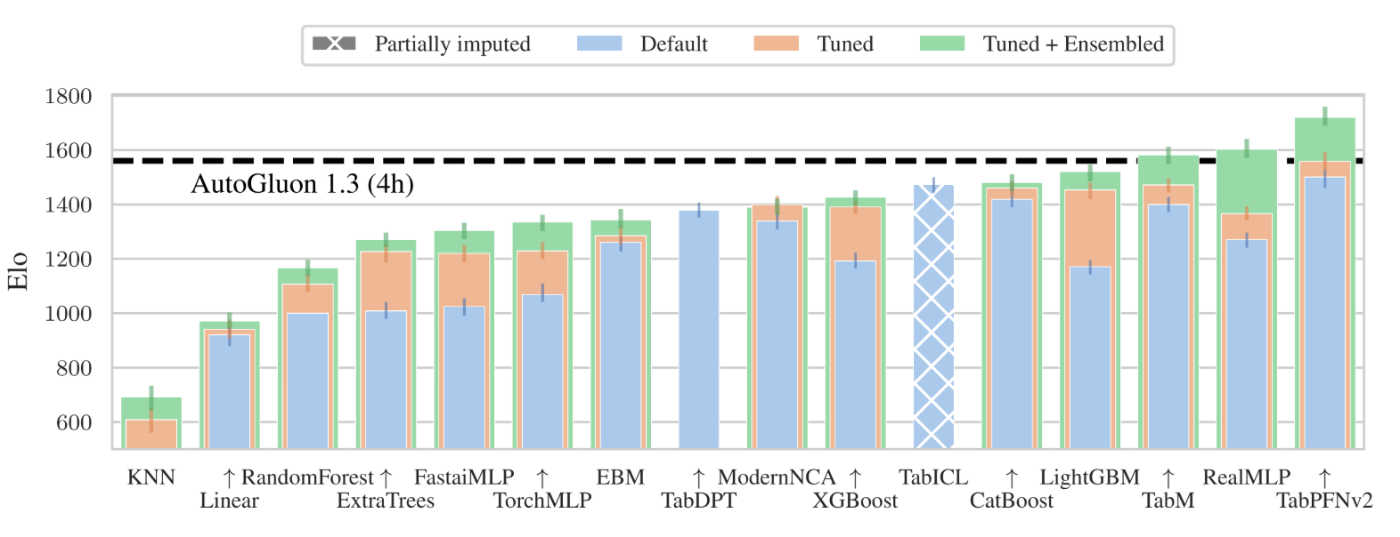
TabPFNが対応可能なデータセットでのリーダーボード: デフォルト設定でも、アンサンブルでも、TabPFNが最も高い性能になっている。TabArenaサイトより引用。
さいごに
軽い気持ちでまとめ始めたのですが、どの論文にもそれぞれの面白さがあり、気づけばとんでもない大長文になってしまいました。
有望手法をまとめていて感じたこととしては、テーブルデータ分析に対しては、比較的シンプルなNNモデルベースの手法が有望であるという点です。比較的データサイズが小さいことが多いテーブルデータの特性を鑑みると、自然言語や画像認識のようにTransformer一強という状況でもないということが分かりました。
一方で、TabPFNのように、データセット全体を対象に一気に学習・予測を行うTransformerベースの基盤モデルも出現しており、この方向性についても今後の発展が非常に楽しみです。
これからテーブルデータの予測を行う時には、本記事で紹介したような最新NNモデルについても思い出して、試してみていただけると幸いです。
最後まで読んでいただきありがとうございました。
Discussion