LLM-in-the-loop最適化 -明日の献立をLLMで最適化してみる-

はじめに

こんにちは、株式会社松尾研究所シニアデータサイエンティストの大西です。
この記事は、松尾研究所 Advent Calendar 2025の記事です。

前職でブラックボックス最適化やHuman-in-the-loop最適化に関する研究開発に携わり、現職ではLLM（大規模言語モデル）を用いたプロジェクトを推進しています。これらの経験と昨今のLLMの進展に伴い、私自身が注目している研究テーマをブログにまとめました。

本記事では、従来の最適化と LLM による選好評価を組み合わせた LLM-in-the-loop最適化 を紹介します。近年、LLMを最適化アルゴリズムに組み込み、人間のような判断や選好を反映させるアプローチが注目されています。従来の最適化手法では数値的な目的関数に基づく評価が中心でしたが、LLM を介在させることで、自然言語による柔軟な評価・探索が可能になります。

今回、献立の理想的なPFCバランス（タンパク質・脂質・炭水化物）を数式で最適化し、「組み合わせの良さ」や「満足度」といった定性的な要素をLLMが評価するアプローチを実装してみました。最適化問題では、すべての目的関数を数式で表せるとは限りません。特に「組み合わせの良さ」や「満足度」といった人間の主観的な評価は定量化が難しく、従来の最適化手法では扱いが困難でした。
この枠組みは、献立の最適化以外にも応用可能です。たとえば、デザイン最適化、広告配置、商品レコメンド、UI改善、経営戦略シミュレーションなど、人間の主観や感覚的要素を含む複合的な最適化課題に拡張できます。

関連研究

LLM を最適化ループに組み込む研究は、近年Human-in-the-loopの効率化、最適化アルゴリズムとの統合といった観点で発展しています。本節では、本記事と特に関連の深い研究をいくつか紹介します。

Human-in-the-loopの効率化に関する研究の一つが Agent-in-the-Loop^[1] です。これは企業のカスタマーサポート応答を対象に、LLMが生成した応答を人間エージェントが評価・修正し、そのフィードバックを継続的な学習に活用する「データ・フライホイール」構造を提案しています。実運用の中でフィードバックループを回すことで、モデルの継続的改善を実現しています。

最適化アルゴリズムとLLMをの統合した研究もいくつか行われています。
例えば LLINBO^[2] は、LLMを人間評価者の代替として組み込み、ベイズ最適化（BO）の中で候補案の良し悪しを自然言語で判断させる手法を提案しています。LLMが出力した評価を確率的なスコアとしてBOに取り込み、主観的な目的関数を扱える最適化を実現しました。これにより、定量的な数値で表しにくいタスク（デザイン・文章・UIなど）でも、安全かつ体系的に最適化を進めることが可能になります。
また、AutoLead^[3] では化学分野の分子設計において、LLM が候補生成・探索方向決定を支援する多目的最適化フレームワークを示しています。
さらに LILO^[4] では、ユーザーからの自然言語フィードバックを直接最適化ループに取り込み、対話的に探索を進める方式を提示しています。

多目的最適化とは

多目的最適化とは、複数の相反する目的関数を同時に最適化する手法です。

通常の最適化（単目的最適化）：

# 1つの目的関数を最小化
minimize f(x)

多目的最適化：

# 複数の目的関数を同時に最適化
minimize [f1(x), f2(x), f3(x), ...]

たとえば「理想的な献立」を考えると、PFCバランス・味・満足度・カロリーといった複数の目的を同時に最適化する必要があります。今回は以下の5つの目的関数と1つの制約を設定しました。最小化問題とするため、f4,f5については 1 - scoreという形にしています。また、今回は総カロリーについては制約条件g1として扱うことにしました。

種別	内容	指標（小さいほど良い）
f1	たんぱく質比率を理想(20%)に近づける	|P - 20|[%]
f2	脂質比率を理想(20%)に近づける	|F - 20|[%]
f3	炭水化物比率を理想(60%)に近づける	|C - 60|[%]
f4	献立の組み合わせの良さ（LLM評価）	1 - compatibility
f5	献立の満足度（LLM評価）	1 - satisfaction
g1	総カロリー制約（制約条件）	500–700 kcal/食

このうち f1-f3 は栄養学的な定量評価、f4-f5 は LLM による定性評価として扱います。これらは互いにトレードオフの関係にあり、単一の最良解は存在しません。

単目的化手法とパレート最適化手法の違い：

多目的最適化には大きく2つのアプローチがあります。

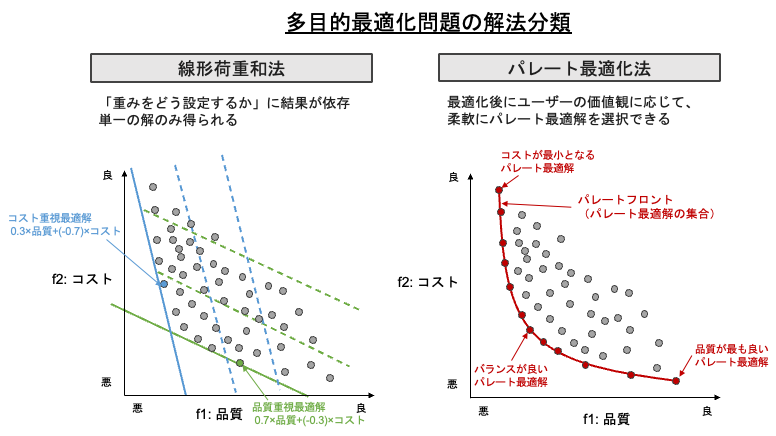
多目的最適化問題の解法分類
1つは、線形加重和法のように複数の目的に重みを設定して足し合わせ、単一の目的関数に変換して最適化する手法です。もう1つは、NSGA-IIなどの進化的アルゴリズムを用いて、複数目的のバランスを考慮しながらパレートフロント（非劣解集合）を直接推定する 「パレート最適化手法」 です。

たとえば線形荷重和法では、「コストを最小化しつつ品質を最大化したい」とき、総合スコア = 0.7×品質+(-0.3)×コスト のように重みを決めて1つの評価値にまとめます。ただし、この方法では「重みをどう設定するか」に結果が大きく依存してしまいます。重みが変われば“最適解”も変わるため、複数の価値基準を想定通りに扱うのが難しいという課題があります。
一方、パレート最適化手法では、重みを事前に決める代わりに 「どの目的も他を犠牲にせずにこれ以上改善できない状態（パレート最適解）」 を複数同時に探索します。このようにして得られた パレートフロント には、コスト重視・品質重視といった異なるトレードオフの解が並びます。そのため、後からユーザーの価値観に応じて、柔軟に“最も望ましい解”を選択できる という利点があります。

多目的最適化の課題

1. すべての目的関数を定量化することが難しい

従来の多目的最適化では、評価関数をすべて数式で表現しようとしてきました。しかし、「美味しさ」「満足度」「食材の組み合わせ」などを数式化するのは極めて困難であり、個人的な好み夜間感覚を反映できないという課題がありました。

2. Human-in-the-loop (HITL) 評価の非効率さ

多目的最適化では、最終的な意思決定は人間が担う必要があります。
また、Human-in-the-loop (HITL) 型の最適化では、最適化の探索途中に人間の評価を行う必要があります。
つまり、探索中・最適化後に得られる「パレート最適解」の中から、自身の優先順位に応じて最適なものを選ぶのが人間の役割です。
しかしこのHITL型の評価には、次のような実用上の課題があります。

• 数十〜数百の献立候補を1つずつ評価するのは現実的でない
• 人間は疲労や気分によって評価基準がブレやすい

本記事の提案：LLM-in-the-loop最適化

LLM-in-the-loop最適化
これらの課題を解決するために、本記事ではLLMを評価関数（evaluator）として多目的最適化ループに組み込むという新しいアプローチを提案します。
具体的には、①献立候補の提案→②評価値の計算→③評価値の反映という最適化フローにおいて、②評価値の計算における定量的な評価を最適化アルゴリズムで行い、定性的な評価をLLMによって自動化する仕組みを提案します。

モデル選択	対応する目的関数
最適化モデル（高速・正確・低コスト）	f1-f3（PFCバランス）
LLM評価器（定性的な評価）	f4-f5（組み合わせの良さ・満足度）

定量的で計算可能な部分は高速・正確に処理し、定性評価のみLLMを活用してコスト削減を実現可能です。また、LLMを評価器として使用することで上記の従来課題についても解決が可能です。

• 人間の介入なしで探索中の評価自動化が可能で、献立候補が増えても対応可能
• 評価基準のブレをある程度制御することができ、複数のLLMで評価することも可能。

最適化ライブラリの選定

多目的最適化を実装する際には、いくつかのライブラリ候補があります。
本セクションでは主要な選択肢を比較し、今回のテーマに最も適したライブラリを選定します。

ライブラリ	言語	ライセンス	商用利用	Githubリンク	特徴
pymoo	Python	Apache 2.0	可能	https://github.com/anyoptimization/pymoo	進化計算ベースの手法が豊富
Optuna	Python	MIT	可能	https://github.com/optuna/optuna	開発が活発、複数の最適化アルゴリズムを選択可能
PlatEMO	MATLAB	記載なし	×（研究用途と明記）	https://github.com/BIMK/PlatEMO	アルゴリズム数は最大規模だが研究用途

今回の実験では進化計算ベースの多目的最適化での実装を想定したこと、私自身が使用した経験があることからpymooを採用しましたが、Optunaでも同様の実験・検証は可能です。
pymoo は多目的最適化に特化したPythonライブラリで、次のような特徴があります。

• 多目的最適化（NSGA-II, NSGA-III, MOEA/Dなど）を標準サポート
• 多様な制約条件・目的関数を簡潔に定義可能
• 結果の可視化（パレートフロント、収束過程など）が容易
• 最適化アルゴリズムごとのドキュメントが充実しており実装例も豊富

プログラム例：

from pymoo.core.problem import Problem
from pymoo.algorithms.moo.nsga2 import NSGA2
from pymoo.optimize import minimize
import numpy as np

class MyProblem(Problem):
    def _evaluate(self, X, out, *args, **kwargs):
        out["F"] = np.column_stack([f1(X), f2(X), f3(X)]) 

algorithm = NSGA2(pop_size=100)
res = minimize(MyProblem(), algorithm, ('n_gen', 50))

実験

使用したデータ

今回、こちらの久留米市オープンデータセットを使用します。
https://data.bodik.jp/dataset/402036_0009100_00005

実験方法

本節では、最適化のみとLLM-in-the-loop最適化のアプローチを比較します。

手法	説明
最適化のみ	栄養に関するPFCバランスの3目的を最適化する
LLM-in-the-loop最適化	上記に加え、LLMが「組み合わせの良さ」「満足度」を評価し5目的を最適化する

①献立候補の提案→②評価値の計算→③評価値の反映というフローで最適化を行います。
①献立候補の提案
多目的最適化アルゴリズムであるNSGA-II^[5]を用いて、主食・主菜・副菜の3変数を対象とした最適化を行います。popsize（候補献立数）=50, 世代数（最適化試行回数）=40として全3seed値で最適化を行いました。
②評価値の計算
前述した5つの評価値をもとに計算を行います。献立の理想的なPFCバランス（タンパク質・脂質・炭水化物）f1-f3を数式で最適化し、「組み合わせの良さ」や「満足度」といった定性的な要素をLLMが評価するアプローチを実装します。最適化のみの場合はf4=0, f5=0としました。
LLMについては、GPT-4o-miniを使用し、プロンプトは以下のように簡潔に設定しました。

Rate compatibility (how well the dishes go together as a meal) and satisfaction (overall appeal and enjoyment) of this 3-dish Japanese meal as floats in [0,1].

③評価値の反映
②評価値の計算で得られた評価値を最適化アルゴリズムに反映し、再度 ①献立候補の提案を行います。このフローを40世代分繰り返し、最終的に得られた献立の差分を人間が定性的に判断します。

プログラム

最適化関数

class RecipeOptimization(Problem):
    def __init__(self, staple_food_df, main_dish_df, side_dish_df):
        super().__init__(
            n_var=3,
            n_obj=5,
            n_constr=1,
            xl=np.array([0, 0, 0]),
            xu=np.array([len(staple_food_df) - 1, len(main_dish_df) - 1, len(side_dish_df) - 1])
        )
        self.staple_food_df = staple_food_df
        self.main_dish_df = main_dish_df
        self.side_dish_df = side_dish_df
        self.ideal_pfc_ratio = np.array([20, 20, 60])

    def _evaluate(self, X, out, *args, **kwargs):
        f1 = np.zeros(X.shape[0])
        f2 = np.zeros(X.shape[0])
        f3 = np.zeros(X.shape[0])
        f4 = np.zeros(X.shape[0])  # ← LLM: compatibility (1-score)
        f5 = np.zeros(X.shape[0])  # ← LLM: satisfaction  (1-score)
        g  = np.zeros((X.shape[0], self.n_constr))

        # ★ 追加：バッチ評価用の入れ物
        prompts = []
        ids = []

        for i in range(X.shape[0]):
            staple_index = int(X[i, 0])
            main_index   = int(X[i, 1])
            side_index   = int(X[i, 2])

            staple_item = self.staple_food_df.iloc[staple_index]
            main_item   = self.main_dish_df.iloc[main_index]
            side_item   = self.side_dish_df.iloc[side_index]

            total_energy  = staple_item['エネルギー[キロカロリー]'] + main_item['エネルギー[キロカロリー]'] + side_item['エネルギー[キロカロリー]']
            total_protein = staple_item['たんぱく質[グラム]']       + main_item['たんぱく質[グラム]']       + side_item['たんぱく質[グラム]']
            total_fat     = staple_item['脂質[グラム]']             + main_item['脂質[グラム]']             + side_item['脂質[グラム]']
            total_carb    = staple_item['炭水化物[グラム]']         + main_item['炭水化物[グラム]']         + side_item['炭水化物[グラム]']

            energy_protein = total_protein * 4
            energy_fat     = total_fat * 9
            energy_carb    = total_carb * 4

            epsilon = 1e-6
            total_energy_with_epsilon = total_energy + epsilon

            percent_protein = (energy_protein / total_energy_with_epsilon) * 100
            percent_fat     = (energy_fat     / total_energy_with_epsilon) * 100
            percent_carb    = (energy_carb    / total_energy_with_epsilon) * 100

            f1[i] = np.abs(percent_protein - self.ideal_pfc_ratio[0])
            f2[i] = np.abs(percent_fat     - self.ideal_pfc_ratio[1])
            f3[i] = np.abs(percent_carb    - self.ideal_pfc_ratio[2])

            # 制約：500-700 kcal
            lower_bound, upper_bound = 500, 700
            g[i, 0] = max(0, lower_bound - total_energy, total_energy - upper_bound)

            # LLM用プロンプト（compatibilityとsatisfaction）
            rid = f"{int(staple_index)}-{int(main_index)}-{int(side_index)}"
            ids.append(rid)
            prompts.append(
                f"Meal: {staple_item['料理名']}, {main_item['料理名']}, {side_item['料理名']}. "
                "Rate compatibility (how well the dishes go together as a meal) and satisfaction (overall appeal and enjoyment) of this 3-dish Japanese meal as floats in [0,1]. " # compatibilityとsatisfactionの説明を追加
                "Return ONLY JSON array element with keys: id, compat, satisfaction."
            )

        # 個体群まとめて一括評価（1世代=1 API呼び出し）
        id2obj = call_llm_api_batch(list(zip(ids, prompts)))

        # LLMスコアを目的関数へ反映（未取得は 0.5 フォールバック）
        for i, rid in enumerate(ids):
            f4[i], f5[i] = id2obj.get(rid, (0.5, 0.5))

        out["F"] = np.column_stack([f1, f2, f3, f4, f5])
        out["G"] = g

最適化プログラム

from pymoo.algorithms.moo.nsga2 import NSGA2
from pymoo.operators.sampling.rnd import IntegerRandomSampling
from pymoo.operators.crossover.sbx import SBX
from pymoo.operators.mutation.pm import PM
from pymoo.termination import get_termination
from pymoo.optimize import minimize

# Instantiate the problem with the filtered dataframes
problem = RecipeOptimization(staple_food_df, main_dish_df, side_dish_df)

algorithm = NSGA2(
    pop_size=50,
    sampling=IntegerRandomSampling(),
    crossover=SBX(),
    mutation=PM(),
    eliminate_duplicates=True
)

termination = get_termination("n_gen", 40)

# Run the optimization
print("Running optimization...")
res = minimize(problem,
               algorithm,
               termination,
               seed=seed_value,
               verbose=True)

pymoo_X = res.X
pymoo_F = res.F

print("Optimization finished.")

実験結果

最適化の結果、それぞれ合計3seed分の150個の献立を得ました。
それぞれ具体的な献立の傾向を見てみます。

最適化のみ
3目的の最適化問題ということもあり、PFCバランスが良い食事群が選ばれています。
一方で、組み合わせの良さや満足度については考慮されない献立となっています。

主食	主菜	副菜	Protein %	Fat %	Carb %	Total Energy
かけそば	蓮根ハンバーグ	きのこのおろし和え	20.5	19.1	59.7	557
巻き寿司	揚げ鮭のマリネ	しいたけの網焼き（3枚）	17.5	20.0	61.1	585
冷やし中華	甘えびの刺身（5尾）	小松菜のお浸し	19.1	19.2	58.8	516

LLM-in-the-loop最適化
LLM を評価器として組み込んだ最適化では、主食の種類を軸にした特徴的な献立が作成されました。

• 和食パターン（PFCバランス型）
  → 栄養・組み合わせの良さ・満足度が最もバランス良い構成

主食	主菜	副菜	Protein %	Fat %	Carb %	Total Energy
五目炊き込みご飯	鶏むね肉の味噌ダレ焼き	さつまいものレモン煮	19.2	18.5	59.2	551
ちらし寿司	かんぱちの刺身（5切）（醤油付き）	小松菜と桜えびの炒め煮	22.1	14.8	59.7	607
麦ごはん	肉じゃが	切干大根の煮物	10.3	26.2	60.1	673
ごはん（中茶碗1杯）	筑前煮	ほうれん草のごま和え	13.0	19.1	65.3	523

• パン＋カツの組み合わせ（満足度型）
  → 高脂質・低炭水化物だが、満足感を重視した構成

主食	主菜	副菜	Protein %	Fat %	Carb %	Total Energy
トースト（食パン6枚切り1枚）	ヒレカツ（ソース付き）	揚げ出し豆腐（2分の1丁）	20.0	46.3	31.0	668
トースト（食パン6枚切り1枚）	とんカツ（ソース付き）	冷奴（3分の1丁、しょうゆかけ）	20.0	50.7	26.6	620

• 麺＋天ぷら／和食の組み合わせ（伝統的整合型）
  → 炭水化物多めだが、味の一貫性がある自然な和食構成

主食	主菜	副菜	Protein %	Fat %	Carb %	Total Energy
かけうどん	エビの天ぷら（大根おろし天つゆ付き）	小松菜とこんにゃくのごま和え	21.4	21.2	52.4	650
かけそば	ブリ大根	わかめとレタスのポン酢和え	20.3	24.1	51.5	638

まとめ・今後

本記事では、 「定量的な最適化」×「定性的なLLM評価」 を統合した LLM-in-the-loop最適化 を実装・検証しました。PFC バランスなどの栄養指標を従来の最適化アルゴリズムで扱い、「組み合わせの良さ」「満足度」といった主観的指標を LLM に評価させることで、数値最適化だけでは得られにくい、「和食」「パン＋カツ」など感覚的に自然な献立案が生成されることを確認しました。その一方で、PFCバランスはわずかに理想から外れるなど、“栄養バランス” と “人間らしい納得感” の間のトレードオフも可視化されました。

今後は、より多様なデータセットの活用、LLMのペルソナ設定やプロンプト設計・評価設計改善、最適化アルゴリズム改善などにより、さらに納得感がある結果が得られると考えられます。LLM 評価の設計については Yan (2025)^[6] による Product Evals in Three Simple Steps の知見が参考になります。

• まず少数の実データに対して N段階評価ではなく pass/fail や win/lose/tie（引き分けあり）の二値・ペアワイズ評価でラベリングすること
• ラベルを用いて 評価軸ごとに個別の LLM evaluator を調整し、「5軸まとめて見るGod Evaluator」は作らないこと
• evaluator は通常のMLモデルと同様に train/test split で検証し、Cohen’s Kappa が 0.7 程度あれば実務上は十分

こうした枠組みは、本記事の LLM-in-the-loop 最適化をプロダクト開発やPoCに展開していく際の実務的な指針にもなります。もし、同様のアプローチを自社の意思決定やプロダクト設計・PoCで試してみたい方がいれば、ぜひお気軽にご相談ください！

脚注

1. Agent-in-the-Loop: A Data Flywheel for Continuous Improvement in LLM-based Customer Support

2. LLINBO: Trustworthy LLM-in-the-Loop Bayesian Optimization

3. AutoLead: An LLM-Guided Bayesian Optimization Framework for Multi-Objective Lead Optimization

4. LILO: Bayesian Optimization with Interactive Natural Language Feedback

5. A fast and elitist multiobjective genetic algorithm: NSGA-II

6. Yan, Ziyou. (Nov 2025). Product Evals in Three Simple Steps. eugeneyan.com.