LoRAの進化：基礎から最新のLoRA-Proまで

近年、大規模言語モデル（LLM）のオープンソース化が進み、大小さまざまなモデルが利用できるようになりました。
これらのモデルは汎用性が高い一方で、特定分野に特化したモデルを作るためのファインチューニングの需要も増えています。

そこで注目されているのが、パラメータ効率的ファインチューニング（PEFT）です。特にLoRA（Low-Rank Adaptation） という手法が広く使われています。LoRAは学習するパラメータ数を大幅に削減できる優れた手法ですが、フルファインチューニング（すべてのパラメータを学習する方法）と比べると性能が劣るという課題があります。
この課題を解決するため、ICLR2025でLoRA-Proという新手法が提案されました。論文を確認する過程でLoRAには派生手法が数多くあることが分かったので、備忘録も兼ねて記事を書いています。
本記事では、LoRAの基本概念から始め、様々な派生手法を整理しながら、LoRA-Proについて解説します。

サマリー

• LoRA派生手法の分類

  • スケーリング・学習率調整型：
    • LoRAのアダプター行列に適用されるスケーリングファクターや学習率を調整し、学習の安定性と速度を改善
  • 構造変更型：
    • LoRAの基本構造そのものを改良し、性能向上
  • 勾配最適化・初期化型：
    • LoRAの最適化プロセスやアダプター行列の初期化を改良することで、フルファインチューニングの学習を模倣（LoRA-Proはここに分類）

• LoRA-Proの特徴

  • LoRAの勾配をフルファインチューニングの勾配に近づける最適化を実現
  • 性能面では既存手法を上回る結果を達成
  • ただし、現時点ではDeepSpeedの独自実装のみ公開されており、既存のPEFTエコシステムとの統合に課題

主要な派生手法の比較表 (LoRA-Pro論文でベンチマーク対象手法）

手法	公開年	中心的なアイデア	アプローチ分類	PEFT公式実装
AdaLoRA	2023	重要度スコアに基づきモジュールごとに動的にランクを調整	構造変更	⚪︎
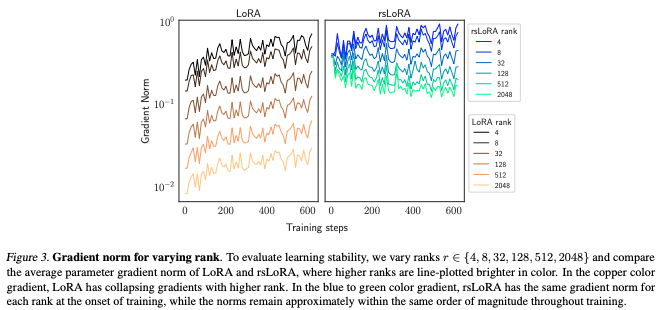
rsLoRA	2023	スケーリングファクターの修正で高ランクでの勾配崩壊を防ぐ	スケーリング調整	⚪︎
DoRA	2024	重み行列をマグニチュードと方向に分解して最適化	構造変更	⚪︎
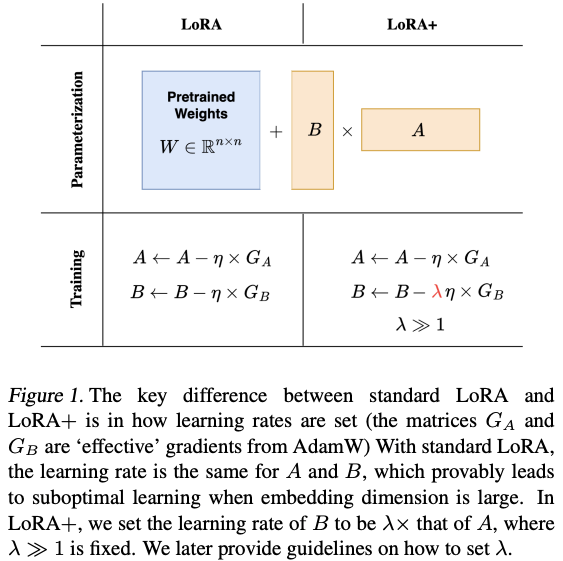
LoRA+	2024	AとB行列に異なる学習率を適用	学習率調整	⚪︎
PiSSA	2024	重み行列の主要な特異ベクトルでアダプターを初期化	初期化（静的最適化）	⚪︎
LoRA-GA	2024	訓練の最初のステップで勾配方向をフルFTに近似	初期化（静的最適化）	×
LoRA-Pro	2024	LoRAの最適化をフルFTの「低ランク仮想勾配」に近似	勾配最適化（動的最適化）	×

各図表は言及がない場合、対応する論文から引用しています。

LoRA(2021)

https://arxiv.org/abs/2106.09685

LoRA（Low-Rank Adaptation）は、ファインチューニング中にモデルの重み行列で生じる変化が、実は低ランクの構造を持つという仮説に基づいています。

LoRAの仮説背景

先行研究①②では、深層学習モデルが非常に多くのパラメータ（高い次元の空間）を持っているにもかかわらず、そのモデルの実効的な複雑さや、学習された表現が占める空間が、パラメータの総数よりもはるかに少ない次元で特徴づけられることを示唆しています。
LoRAは先行研究の知見をもとに、LLMの事前学習済みの重みは固定したまま、各層に非常に小さいアダプター行列を注入することで、タスク特化型のファインチューニングが可能と提案しています。

このアイデアを実装するために、事前に訓練された重み行列 $W_0 \in \mathbb{R}^{m \times n}$ を凍結し、変更分 $\Delta W$ を2つの小さな低ランク行列 $B \in \mathbb{R}^{m \times r}$ と $A \in \mathbb{R}^{r \times n}$ の積として再パラメータ化します。

この関係は、スケーリングファクター $s$ を用いて以下の式で表されます

$W = W_0 + \Delta W \approx W_0 + sBA$

これにより、訓練パラメータ数を $m \times n$ から $r \times (m+n)$ に大幅に削減でき、計算コストとメモリ消費を抑えてモデル学習が可能になりました。しかし、LoRAにはフルファインチューニングに性能が及ばないという根本的な課題が残されていました。

LoRAの派生手法：様々なアプローチ

LoRAの性能をさらに高めるため、さまざまな改良手法が提案されてきました。これらの手法は、主に以下の3つのアプローチに分類できます。

1. スケーリング・学習率調整に基づく手法

rsLoRA (2023)

https://arxiv.org/abs/2312.03732

• モチベーション： LoRAの性能・学習安定性向上
• 中心的なアイデア: 従来のLoRAのスケーリングファクター $s = \alpha/r$ が、ランク $r$ が増加するにつれて勾配を小さくし、学習が停滞する「勾配崩壊」を引き起こすことを発見
• アプローチ: 新しいスケーリングファクター $s = \alpha/\sqrt{r}$ を提案し、高ランク設定における学習の安定性を確保
  

LoRA+ (2024)

https://arxiv.org/abs/2402.12354

• モチベーション： LoRAの性能・学習安定性・収束速度向上
• 中心的なアイデア: アダプター行列 $A$ と $B$ に同じ学習率を適用することが、効率的な学習を妨げる可能性を指摘
• アプローチ: $A$ と $B$ に異なる学習率を適用することを提案し、LoRAと同じ計算コストで収束速度と最終的な性能を改善
  

2. 構造変更に基づく手法

AdaLoRA (2023)

https://arxiv.org/abs/2303.10512

• モチベーション： LoRAの性能向上
• 中心的なアイデア: すべてのモジュールに一律のランク$r$を割り当てるのではなく、各モジュールの重要度に基づき動的にランクを調整
• アプローチ: アダプター行列をSVD（特異値分解）の形式に変更し、重要度の低い特異値を動的に刈り込む
  • $W = W_0 + \Delta W = W_0 + P\Lambda Q$
    • ここで、$W_0$は事前学習済み重みを表し、増分更新$\Delta W$は、左特異ベクトル$P \in \mathbb{R}^{d_1 \times r}$、特異値$\Lambda \in \mathbb{R}^{r \times r}$、および右特異ベクトル$Q \in \mathbb{R}^{r \times d_2}$に分解

SVDとは

SVD（Singular Value Decomposition, 特異値分解）は、任意の行列を3つの行列の積に分解する手法です。
行列 $W$ をSVDで分解すると：

$W=P\Lambda Q$

• $P$：左特異ベクトル（行方向の重要なパターン）
• $\Lambda$：特異値を並べた対角行列（各パターンの重要度）
• $Q$：右特異ベクトル（列方向の重要なパターン）

特異値（$\Lambda$の対角成分）は大きい順に並んでおり、値が大きいほどその成分が重要ということを表します。

DoRA (2024)

https://arxiv.org/abs/2402.09353

• モチベーション： LoRAの性能・学習安定性向上
• 中心的なアイデア: フルファインチューニングが重み行列の「大きさ（マグニチュード）」と「方向」を独立して最適化するのに対し、LoRAはこれらを同時に変更するため非効率だと指摘
  • 大きさ：重みベクトルの全体的な強さ・スケールに相当
  • 方向：モデルがどのような特徴を学習しているかに相当
• アプローチ: 事前学習済みモデルの重み(パラメータ)をマグニチュードと正規化された方向行列に分解し、LoRAを方向成分にのみ適用。マグニチュード側は学習可能なスカラーで調整。
  

3. 勾配最適化・初期化に基づく手法

LoRA-GA (2024)

https://arxiv.org/abs/2407.05000

• モチベーション： LoRAの性能・収束速度向上
• 中心的なアイデア: LoRAの収束が遅いのは、学習初期の勾配方向がフルファインチューニングの勾配と乖離しているためだと仮定
• アプローチ: 訓練の最初のステップで、フルファインチューニングの勾配行列の固有ベクトルを 使用してアダプター行列 $A$ と $B$ を初期化し、学習開始時からフルファインチューニングの勾配方向と一致させる
  

PiSSA (2024)

https://arxiv.org/abs/2404.02948

• モチベーション： LoRAの性能・収束速度向上
• 中心的なアイデア: LoRAの「Noise & Zero」初期化($A$ を乱数、$B$をゼロで初期化)が収束を遅らせるという考え
• アプローチ: 訓練開始前に重み行列$W_0$に特異値分解（SVD）を適用し、$W_0$を「主要な低ランク行列 $W_{pri}$」と「残差行列 $W_{res}$」に分解。アダプター行列 $A$ と $B$ は $W^{pri}$ の特異値と特異ベクトルで初期化

LoRA-Pro: フルファインチューニングの勾配を追跡するアプローチ

https://arxiv.org/abs/2407.18242

• モチベーション： LoRAの性能・収束速度向上
• 中心的なアイデア: LoRAによる最適化が、フルファインチューニングにおける「仮想的な低ランク勾配」によるパラメータ更新と数学的に等価であるという発見に基づく

上記理論の仮定

LoRA-Proの理論は、アダプター行列 A と B が学習中にフルランクであるという仮定に基づいています。大規模なファインチューニングデータや特定の事前学習モデルではこの仮定が成立しない可能性があり、性能に影響を与える可能性があります。

LoRA-Proの著者たちはこの仮定が実際に成立するかを実験的に検証しました。

実験内容と結果
Llama-2-7BモデルをMetaMathQAデータセットでファインチューニングする過程で、アダプター行列 $A$ と $B$ のランクがどのように変化するかを追跡しました。ランクは8と32の2つの設定で検証されています。

実験の結果、初期段階では行列 $B$ がゼロ行列として初期化されるため、アダプター行列はフルランクではないものの、最初の更新ステップ後には、両方の行列がフルランクを達成することが観察されました。この挙動は他の層でも同様に確認されています。

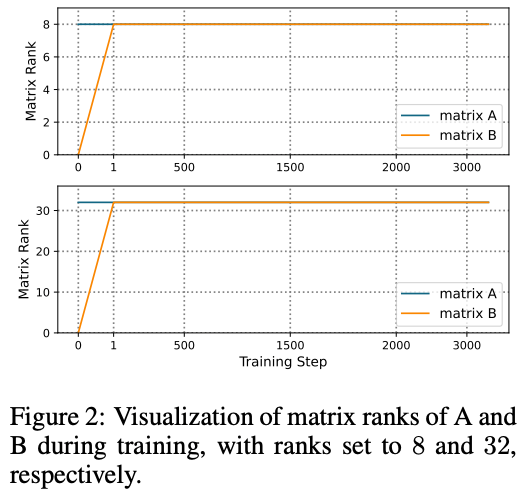
この実験結果より、LoRA-Proの理論の前提となる仮定は問題なく成立すると結論づけられています。

フルランクとは

「フルランク」であるとは、その行列のすべての行ベクトルが線形独立であり、かつすべての列ベクトルも線形独立である状態を指します。

具体例

1. フルランクの行列の例（情報の重複がない、最大限の情報を保持）

   $A = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}$
   この行列の行ベクトルは $(1, 0)$ と $(0, 1)$ です。

   $(1, 0)$ は $(0, 1)$ を何倍しても作れず、その逆も然りです。つまり、これらは線形独立です。
   同様に、列ベクトルも $(1, 0)$ と $(0, 1)$ であり、これらも線形独立です。

   この行列Aは、行の数（2つ）と同じ数の線形独立な行ベクトルを持ち、列の数（2つ）と同じ数の線形独立な列ベクトルを持っています。このような状態を「フルランク」と言います。この行列は、2次元空間の情報を最大限に、かつ重複なく表現しています。

2. フルランクではない行列の例（情報が重複している、一部の情報が失われている可能性）

   $B = \begin{pmatrix} 1 & 2 \\ 2 & 4 \end{pmatrix}$
   この行列の行ベクトルは $(1, 2)$ と $(2, 4)$ です。

   $(2, 4)$ という行ベクトルは、$(1, 2)$ を2倍することで作ることができます（$2 \times (1, 2) = (2, 4)$）。これは、2つの行ベクトルが線形従属である、つまり線形独立ではないことを意味します。
   同様に、列ベクトルも $(1, 2)$ と $(2, 4)$ であり、これらも線形従属です。

   この行列Bは、行の数（2つ）に対して線形独立な行ベクトルが1つしかありません（例えば $(1, 2)$ だけ）。列の数（2つ）に対しても線形独立な列ベクトルが1つしかありません。このような行列は「フルランクではない」と言います。この行列は、2次元空間の情報を表現しているようでいて、実際には1次元の情報しか持っておらず、情報が重複している、あるいは一部の情報が失われている状態と言えます。

• アプローチ: LoRAの勾配が、フルファインチューニングの真の勾配により近づくように最適化し、性能を向上
  • フルファインチューニングの真の勾配 $g = \frac{\partial L}{\partial W}$ と、LoRAの更新によって生じる等価勾配 $\tilde{g} = sBg^A + sg^B A$ との間の距離を最小化する最適化問題を定式化
  • この最適化問題には閉形式解が存在することを理論的に証明。この解は、フルファインチューニングの勾配を明示的に計算することなく、標準LoRAの勾配（$g_{lora}^A$ と $g_{lora}^B$）を用いて最適なアダプター行列の勾配（$g^A$ と $g^B$）を導出
  • これにより、LoRA-Proは学習過程を通じてフルファインチューニングの勾配方向を継続的に追跡し、修正することが可能になる
  • 追加の計算は低ランク行列 $r \times r$ 行列上で行われるため、小規模ではあるが標準LoRAに比べてGPUメモリと訓練時間が追加される

LoRA-Proにおける行列A, Bの最適化ステップ

1. 順伝播と標準勾配の計算

通常のLoRAと同様に、事前学習済み重み $W_0$ とアダプター行列 $A, B$ を用いて順伝播を行い、損失 $L$ を計算します。その後、バックプロパゲーションによって、通常のLoRAの最適化で用いられる標準勾配 $g_{lora}^A$ と $g_{lora}^B$ を求めます。

---

2. 「等価勾配」の定義

LoRA-Proは、LoRAアダプターの更新が、フルファインチューニングにおける「仮想的な低ランク勾配」 $\tilde{g}$ による重み $W$ の更新に等価であるという考えに基づいています。この $\tilde{g}$ は、調整後の勾配 $g^A$ と $g^B$ を用いて、$\tilde{g} = sBg^A + sg^B A$ と定義されます。

---

3. 最適化問題の定式化

LoRA-Proの目的は、この「等価勾配」 $\tilde{g}$ を、フルファインチューニングの真の勾配 $g = \frac{\partial L}{\partial W}$ にできるだけ近づけることです。これを数学的な最適化問題として以下のように定式化します。

$$\min_{g^A, g^B} ||\tilde{g} - g||_F^2$$

ここで、$||\cdot||_F$ はフロベニウスノルム(行列の「大きさ」を測るための尺度のひとつ)です。

---

4. 最適な勾配の導出

上記の最適化問題には、フルファインチューニングの勾配 $g$ を明示的に計算することなく、標準勾配 $g_{lora}^A, g_{lora}^B$ および行列 $A, B$ を用いて表現できる閉形式解が存在します。この解には、任意行列 $X$ が含まれます。

$$g^A = \frac{1}{s^2}(B^T B)^{-1}g_{lora}^A + XA$$

$$g^B = \frac{1}{s^2}[I - B(B^T B)^{-1}B^T]g_{lora}^B(A A^T)^{-1} - BX$$

---

5. 任意行列 $X$ の決定

ステップ4で得られた勾配 $g^A, g^B$ が、標準勾配 $g_{lora}^A, g_{lora}^B$ に近い状態を維持するよう、任意行列 $X$ を決定します。これは別の最適化問題 $\min_X (||g^A - g_{lora}^A||_F^2 + ||g^B - g_{lora}^B||_F^2)$ を通じて行われ、Sylvester方程式を解くことで一意な $X$ が得られます。

---

6. アダプター行列の更新

最後に、ステップ4と5で得られた調整後の最適な勾配 $g^A$ と $g^B$ を用いて、学習率 $\gamma$ に従ってアダプター行列 $A$ と $B$ を更新します。

$$A \leftarrow A - \gamma g^A$$

$$B \leftarrow B - \gamma g^B$$

この一連のプロセスにより、LoRA-Proは損失を着実に減少させながら、フルファインチューニングの勾配方向をより正確に追従し、高い性能を達成します。

精度比較

論文の実験結果は、LoRA-ProがLoRA、LoRA-GA、DoRAなどの他のLoRA派生手法を上回り、特にGLUEベンチマークではフルファインチューニングも上回る性能を示しています。これは、フルファインチューニングが訓練データセットが小さい場合に過学習しやすいのに対し、LoRA-Proがより汎化性能の高い解に収束できるためだと考えられます。

課題と今後の期待

しかし、LoRA-Proの実用化には課題も残されています。理由としては、最適化の過程で勾配を複数ステップに分けて算出する必要があり、Optimizerの処理が複雑になるためです。その結果、公式で提供されているコードは、DeepSpeedの独自実装にとどまっており、広く普及しているPEFTライブラリ（Hugging Faceなど）に直接統合されていないため、気軽に試すことが難しい現状です。

DeepSpeed実装部
https://github.com/mrflogs/LoRA-Pro/blob/main/DeepSpeed-0.15.1/deepspeed/runtime/zero/stage_1_and_2.py#L1828

今後、LoRA-Proの優れたアプローチが、PEFTなど多くの開発者に利用される形で実装されることを期待したいです。（AI codingでこの辺りのハードルは低いかもしれない）