Zenn
🐧

MPPIを用いた四輪独立ステアリング車両の自律移動制御

に公開
robot
制御工学
自動運転
モデル予測制御
独ステ
tech

本記事は名古屋大学の青木瑞穂(https://mizuhoaoki.github.io/)による投稿です.

対象読者

  • 四輪独立ステアリング車両(いわゆる独ステ車両)の自律移動制御に興味がある方
  • 確率最適制御器の一種であるMPPI(Model Predictive Path-Integral, モデル予測経路積分)制御の概要・適用方法・使い方のコツについて, 具体例を通して理解したい方

本記事の概要

四輪独立ステアリング車両を題材に,

  • そもそもどんな車両なのか？
  • 車両の動作を記述する数理モデルの定式化
  • 自律移動を達成する枠組みの構築
  • MPPIを用いた車両制御の達成

について解説します.

具体的には以下の動画に示すような, 「指定したゴール地点に向かって自律的に移動する制御システムはどのように構築すればよいか？」という問いに対する取り組み方の一例を紹介します.

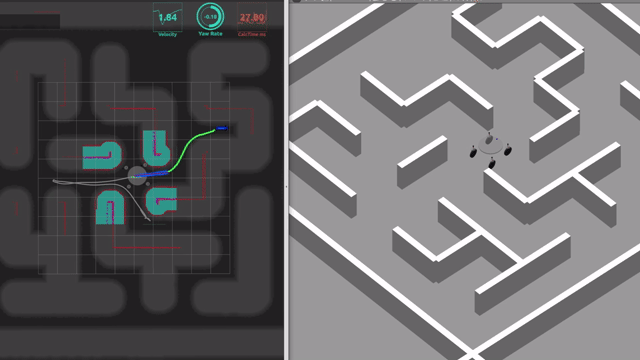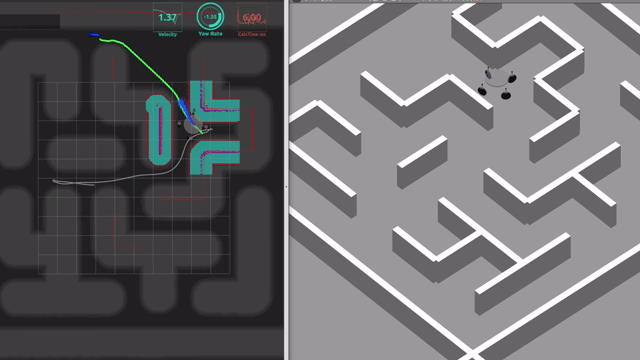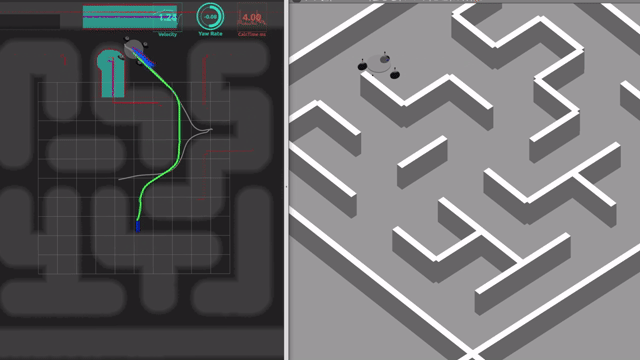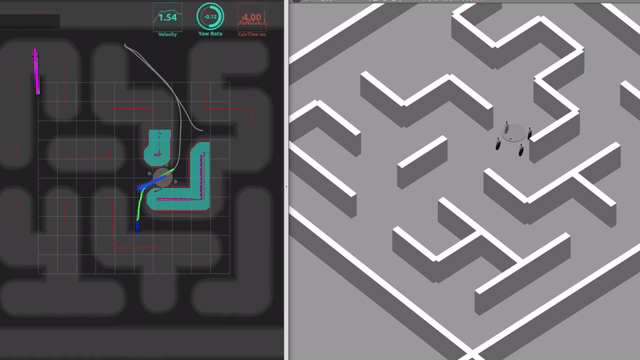
ソースコードは下記のGithubリポジトリで公開しています.
https://github.com/MizuhoAOKI/mppi_swerve_drive_ros
参考文献はM. Aoki, et al. IROS 2024です. ただし, 本記事は論文の内容から学術的な進展部分を差し引いた, 比較的標準的な内容をまとめたものです. どなたかが類似のシステムを構築したいとき, たたき台として参考になると良いな, と思って書きました.

四輪独立ステアリング車両とは？

どんな車両か

四輪独立ステアリング車両とは, 4つの車輪を持ち, それぞれの車輪が独立に操舵・駆動を行える車両を指します. 1つの車輪ユニットに車輪の方向を変える操舵用モータと車輪を回転させ推進力を得る駆動用モータが含まれ, これを4ユニット搭載する構成が一般的です. 1つの車輪あたり2つのモータが必要で, 車輪が4つあるため, 1台の車両を作るのに合計8つのモータが必要になります.

この車両の呼び方は様々ありますが, 本記事では4WIDS車両 (Four-Wheel Independent Drive and Steering Vehicleの略)と呼称します.

[補足] 4WIDS車両の様々な呼び方について

利点・欠点

4WIDS車両の利点として, 車輪の方向を自在に変えることで, どの方向へも高速で移動できる点が挙げられます. 全方向移動はオムニホイール・メカナムホイールなど特殊な形状の車輪を用いて達成する方法もありますが, これらを搭載した車両は4WIDS車両に移動速度において劣る上に, 粗い路面上の走行を苦手としています.

一方で, 4WIDS車両の欠点としては, 機械的構造の複雑さによる設計・制作・整備の難しさが挙げられます.

利点

  • 全方向への高速な移動が可能
  • 粗い地面でも走行可能

欠点

  • 多くのモータとそれを駆動するための電源・回路が必要であり, 制作のコストが高い.
  • 複雑な構造であるため, 設計・制作・整備において難易度が高い.
  • モータが車輪の内部もしくは近くに配置される構造上, 路面から伝わる衝撃や浸水などにより駆動系が故障するリスクが大きい.

利用事例

高速な全方向移動が可能な特性のため, 特に高速なロボットの移動が重要となる競技などでよく採用されます.
[例1] NHK学生ロボコン

その場での回転や真横への移動など通常の(2自由度を持つ)車両では行えない柔軟な動きが可能であるため, 混みあった市街地などを走るのに便利な乗用車としての開発も行われています.
[例2] HYNDAI MOBIS, e-Corner System

狭所を効率的に走行できる能力があるため, 農業用ロボット・家事ロボットとしての開発事例もあります.
[例3] Path Tracking of Agricultural Vehicles Based on 4WIS–4WID Structure and Fuzzy Control
[例4] TidyBot++: An Open-Source Holonomic Mobile Manipulator for Robot Learning

地球外環境で活動するために開発された探査機にも, 同種の機構が採用されています.
[例5] GITAI's rover
高い移動性能の恩恵を受けられるのはもちろん, 冗長な自由度により一部モータが故障しても他のモータにより移動を継続する能力があることも選定の背景にあるのではないか, と筆者は推測しています.

自律移動制御の問題設定

4WIDS車両の自律移動システムを構築するにあたり, まずは問題設定を明確にしましょう.
今回は4WIDS車両の狭い場所を効率的に移動可能であるという特性を踏まえ, 工場内で稼働する搬送用ロボットなどの利用例を想定して以下のように設定しました.

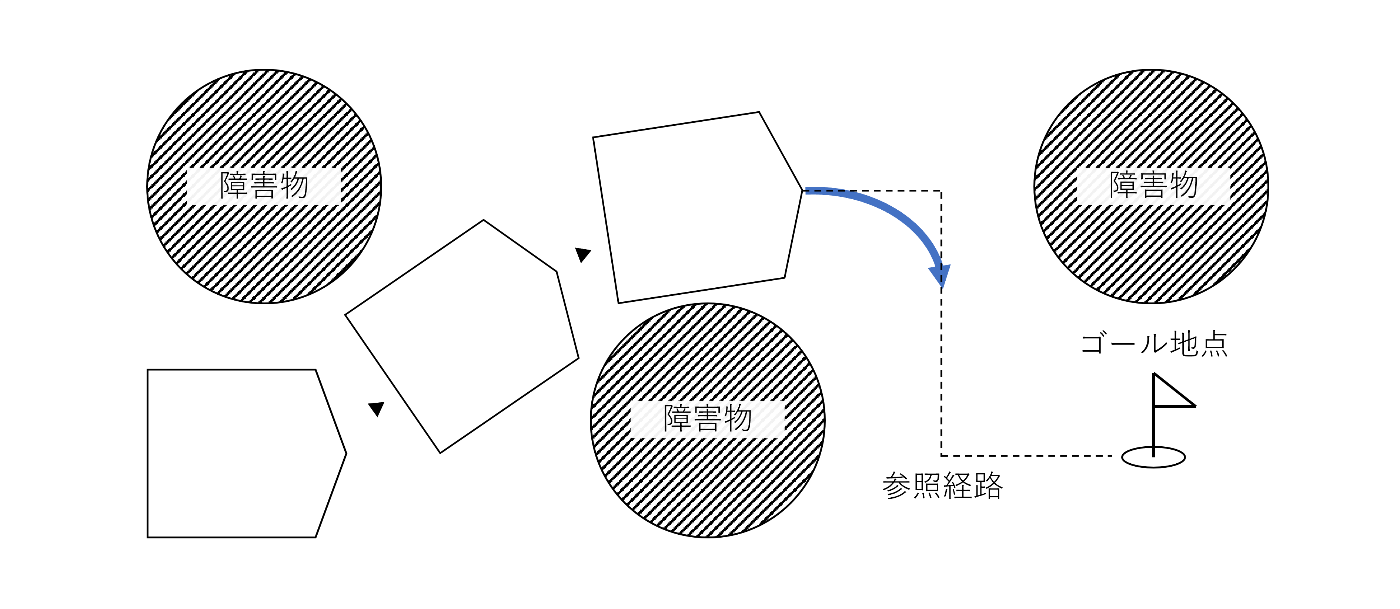
前提条件

  • 走行する環境の地図は事前に与えられる.
  • 与えられた地図上において, 到達すべきゴール地点が指定される.

実現したいこと

  • 与えられたゴール地点へ安全に, 素早く, 滑らかに移動する.

必要な機能

  • 安全性
    • 障害物との衝突を避ける.
  • 素早さ
    • 地図上の現在位置を把握する.
    • 現在位置からゴール地点までの最短経路を通る.
    • できるだけ高速で移動する.
  • 滑らかさ
    • 車両の移動速度が大きく変化しない動作(すなわち, 加速度の小さい動作)を行う.
    • モータに対する制御入力が大きく変化しない制御を行う.

自律移動制御の枠組み設計

問題設定に対応する具体的な自律移動システムの枠組みを設計します.

今回は, 車両の現在位置を知る「自己位置推定」, ゴールまでの最短経路を求める「経路計画」, 計画した経路に滑らかに追従する「車両制御」の3つの機能を組み合わせることで要求を達成しようと考えました.

本記事は制御対象の特殊性ゆえに既存のソフトウェアを利用するだけでは対応が難しいという観点から, 特に車両制御について重視して述べます. 逆に言えば, 車両制御を除いた他の機能は既存のパッケージを組み合わせて利用できます. 今回実装した自律移動システムはROS(Robot Operating System)を用いて実装されており, 公開されている様々な機能を容易にシステムに組み込んで恩恵を受けることができます.

それでは, 以下に模式図と, それぞれの機能に関する解説を示します.

自律移動システム構成図

システムの構成図を以下に示します.
環境地図と地図上のゴール地点を入力すると, 車両が自律的に移動する枠組みです.

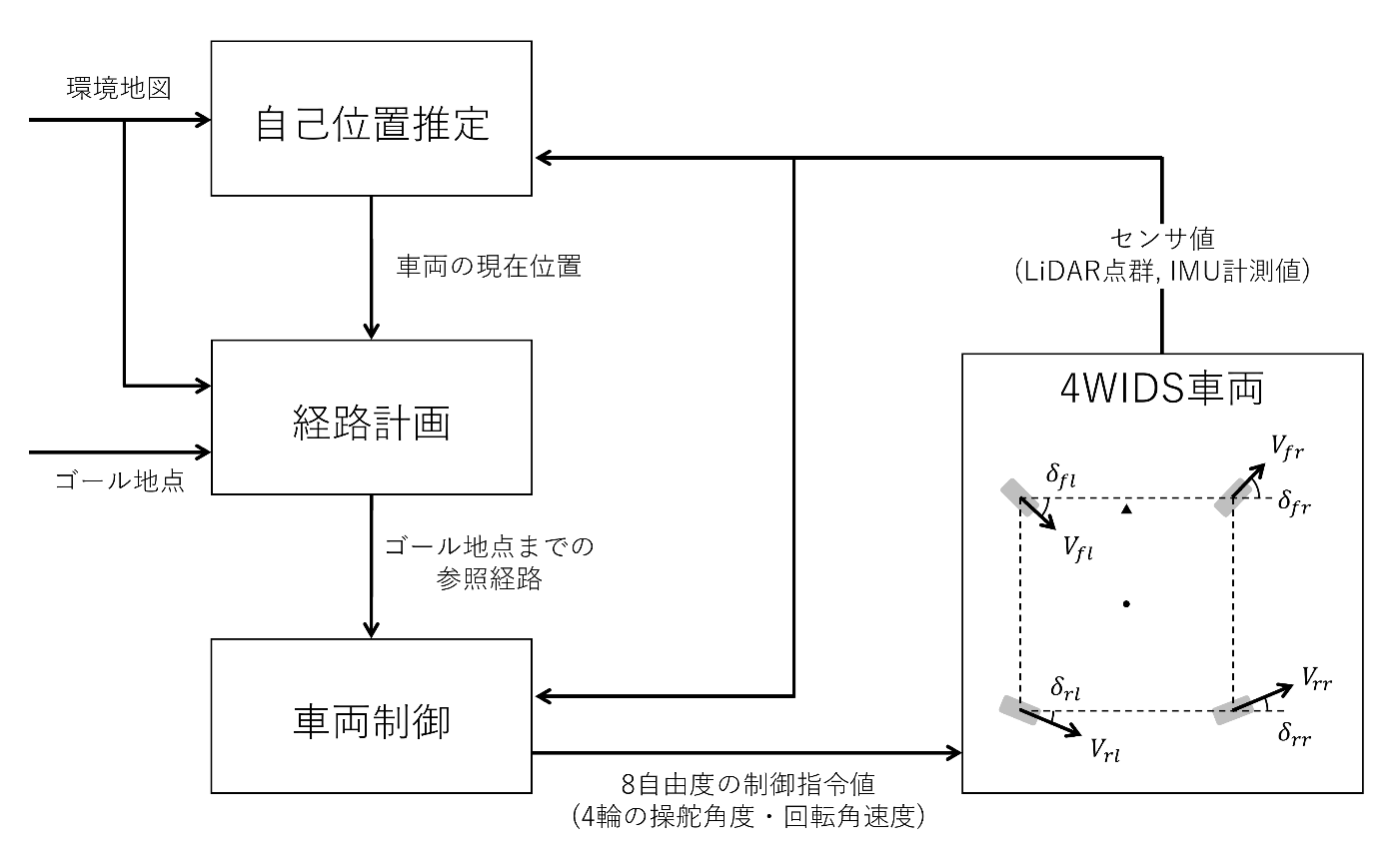
4WIDS車両

まず環境認識に関して, 4WIDS車両は2種類のセンサを搭載すると想定します.
一つ目はLiDAR(Light Detection and Ranging)であり, 周囲に光を照射しその反射光をとらえることで, 周囲の障害物の位置・形状を検知することができます.
二つ目はIMU(Inertial Measurement Unit)であり, 車両の並進加速度や角速度を計測することで, 車両の運動を計測するためのものです.
これらの情報はリアルタイムで頻繁に更新され, 以下で解説する自己位置推定と車両制御の処理で利用されます.

次に制御に関して, 車両は8自由度の制御入力(4輪それぞれの操舵角度・回転角速度)を受け取ると, 指令値を達成するよう内部で制御されるものと想定します. 内部の制御は使用するモータの種類等にも依存する話になりますが, 例えばPID制御をはじめとするフィードバック系により安定した指令値への追従を目指すアプローチをとることが考えられます.

自己位置推定 (手法 : AMCL)

環境地図, LiDARセンサの点群データ, IMU計測値を用いて, 車両が地図上のどこにいるかを推定します. 今回はAMCL(Adaptive Monte Carlo Localization)と呼ばれる手法を採用しました.

経路計画 (手法 : A*)

環境地図, ゴール地点, 現在位置情報を用いて, 地図上の現在位置からゴール地点までの最短経路(下図中の緑線)を計画します. 今回はA*アルゴリズムと呼ばれる手法を採用しました.

経路計画時には障害物を避けつつ最短の経路を通ることしか考慮されていないため, 車両を滑らかに移動させることは車両制御の処理で考慮する必要があります.

車両制御 (手法: MPPI)

現在位置からゴール地点へ向かう参照軌道に滑らかに追従するための制御入力値(4輪の操舵角度・回転角速度指令値)を求めます.
LiDARセンサは検知した周囲の障害物を避けるために, IMU計測値は現在の運動を把握し速度の急峻な変化を抑えるために, それぞれ利用します.

今回の枠組みにおいて車両制御の請け負う機能は,

  • [1] 安全性: LiDARで検出した障害物との衝突を避ける
  • [2] 素早さ: 参照軌道に沿いつつもできるだけ高速で移動する
  • [3] 滑らかさ: 車両の移動速度や車輪の操舵・駆動入力の急変を抑止する

という重要かつ複雑なものです.

時々刻々と変わる状況に対応しながらこれからどう動くかを決めるためには, ある動作をしたときの自車両の少し先の未来を先読みした上で, 最も良さそうな動作を選択する方針が有効です.
このように予測と最適化に基づく制御は モデル予測制御 (Model Predictive Control, MPC) と呼ばれており, 車両だけでなく化学プラント・脚型ロボット・ドローン・ロケットの垂直着陸など, 幅広いシステムの制御に用いられてきました.

MPCで最適な制御入力を求める方法は様々あり, 制御するシステムや問題設定に応じて適切な手法の選択が必要です. 今回はLiDAR点群で表現される障害物形状(微分可能でない表現)・車両制御入力の変動制限(非線形な表現)を扱う必要があることから, MPCの中でも幅広いシステムや問題設定に対応可能なMPPIという手法を選択しました. 次図は4WIDS車両にMPPIを適用した際の可視化です. 車両前方に伸びる複数の青い線は検討した未来の車両運動を示し, 赤い矢印は推定された最も良い近未来の車両運動を示します.

さて, MPCを適用し車両の取るべき未来の最適な行動を計画するには,

  • [1] システムの未来を先読みするための予測モデル
  • [2] 制御入力の良し悪しを判断するための評価関数

の2つが必要です. それぞれ, 順に準備していきましょう.

[MPPI適用準備 1/2] 車両運動のモデル化

[補足] 車両運動のモデル化方針について

本節では, ある制御入力を与えたときの車両状態の変化を予測するための数理モデル, いわゆる予測モデルを準備しましょう. 予測モデルとは, 時刻 t ステップにおける車両状態ベクトル \bm{x}_t, 制御入力ベクトル \bm{u}_t をもとに時刻 t+1 ステップの車両状態を求める数理モデルのことです. 今回は次に示す状態更新式を求めることを目指します.

\bm{x}_{t+1} = F(\bm{x}_t, \bm{u}_t)

上記の状態更新式を定めるには, (1) 車両状態 \bm{x} の定義, (2) 制御入力 \bm{u} の定義, (3) 関数 F の定義, のすべてを行う必要があります. 今回, 車両状態 \bm{x} = [p_x, p_y, \theta]^T, 制御入力 \bm{u} = [v_x, v_y, \omega]^T をそれぞれ定義しました. \bm{x} にはグローバル座標上のx, y位置 p_x, p_y とx軸正方向と車両の正面方向が成す角度 \theta を選定し, \bm{u}には車両状態の単位時間あたり変化量を採用しました. 車両状態・制御入力の定義から, 1時刻ステップの長さ \Delta tを用いて, 状態更新式は次のように表すことができます. ( すなわち, 関数 F が決まります. )

\begin{bmatrix} p_x \\ p_y \\ \theta \end{bmatrix}_{t+1} = \begin{bmatrix} p_x \\ p_y \\ \theta \\ \end{bmatrix}_t + \begin{bmatrix} v_x \\ v_y \\ \omega \\ \end{bmatrix}_t \Delta t

ここで, そもそも4WIDS車両は8自由度を持ち, 実車両に渡す操作指令値の次元は8であることを思い出しましょう. 素直に定式化するなら, 制御入力も操作指令値と同じ次元で定義しても良さそうです. その上であえて制御入力を3次元の変数として定義したのは今回の問題設定において都合の良い性質を持つ解を効率的に探索するための工夫です. 以下で詳しく説明します.

グローバル座標系から見た車両中心の前方向速度v_x, 左方向速度v_y, 角速度\omegaをまとめたベクトルを

\bm{u}_c = [v_x, v_y, \omega]^T,

グローバル座標系から見た4輪それぞれのx, y方向速度をまとめたベクトルを

\bm{u}_w = [ V_{xfl}, V_{xfr}, V_{xrl}, V_{xrr}, V_{yfl}, V_{yfr}, V_{yrl}, V_{yrr}]^T,

4輪の操舵角度\delta_{*}と車輪中心の移動速度V_{*} を

\bm{u}_v = [ \delta_{fl}, \delta_{fr}, \delta_{rl}, \delta_{rr}, V_{fl}, V_{fr}, V_{rl}, V_{rr}]^T,

と表記します. * \in \{ fl, fr, rl, rr \} はある車輪を指定するための記号です.
実際に車両を操作するときに必要になる指令値は \bm{u}_v です.

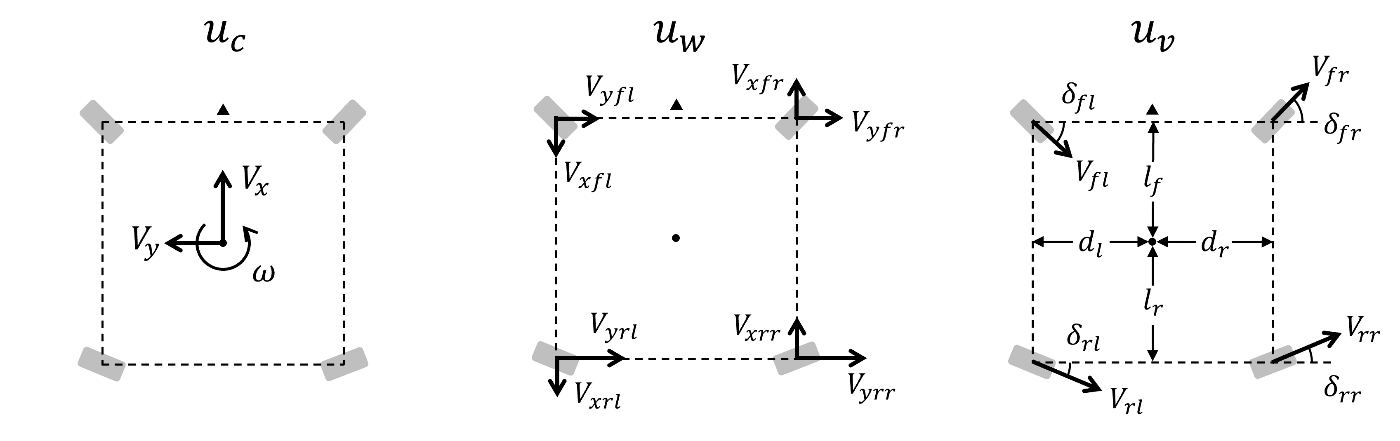
ここで有用な特性として, \bm{u}_cが与えられたとき, 「車両が剛体である」「車輪が滑らない」という拘束の下で, \bm{u}_wは一意に求められます. 実用上も, 比較的低速域での移動であれば, これらの拘束は満たされると想定して問題ない場合が多いです.

この関係は行列\bm{C}_{c \rightarrow w}を用いて以下のように記述されます.

\bm{u}_w = \bm{C}_{c \rightarrow w} \bm{u}_c,
\bm{C}_{c \rightarrow w} = \begin{bmatrix} 1 & 0 & -d_l \\ 1 & 0 & d_r \\ 1 & 0 & -d_l \\ 1 & 0 & d_r \\ 0 & 1 & l_f \\ 0 & 1 & l_f \\ 0 & 1 & -l_r \\ 0 & 1 & -l_r \end{bmatrix}.

また, \bm{u}_w から \bm{u}_v への変換は非線形になるものの, ある車輪 * \in \{ fl, fr, rl, rr \} に対して以下のように得られます. この変換を \bm{u}_v = f_{w \rightarrow v}(\bm{u}_w) と表記します.

\delta_{*} = \arctan{\frac{V_{y*}}{V_{x*}}}, \\ V_{*} = \sqrt{V^2_{x*} + V^2_{y*}},

V_{*} は車輪中心の移動速度ですが, 車輪が滑らないという拘束をおいているため, 車輪半径を R_* とすると回転角速度 \omega_* へ変換可能です.

\omega_{*} = V_{*} / R_*

以上の議論から,「車両が剛体である」「車輪が滑らない」という仮定の下で, 3次元の車両中心速度 \bm{u}_c は8次元の車両制御入力\bm{u}_vに変換できることがわかりました.

\begin{equation} \bm{u}_v = f_{w \rightarrow v}(\bm{C}_{c \rightarrow w}\bm{u}_c) \end{equation}

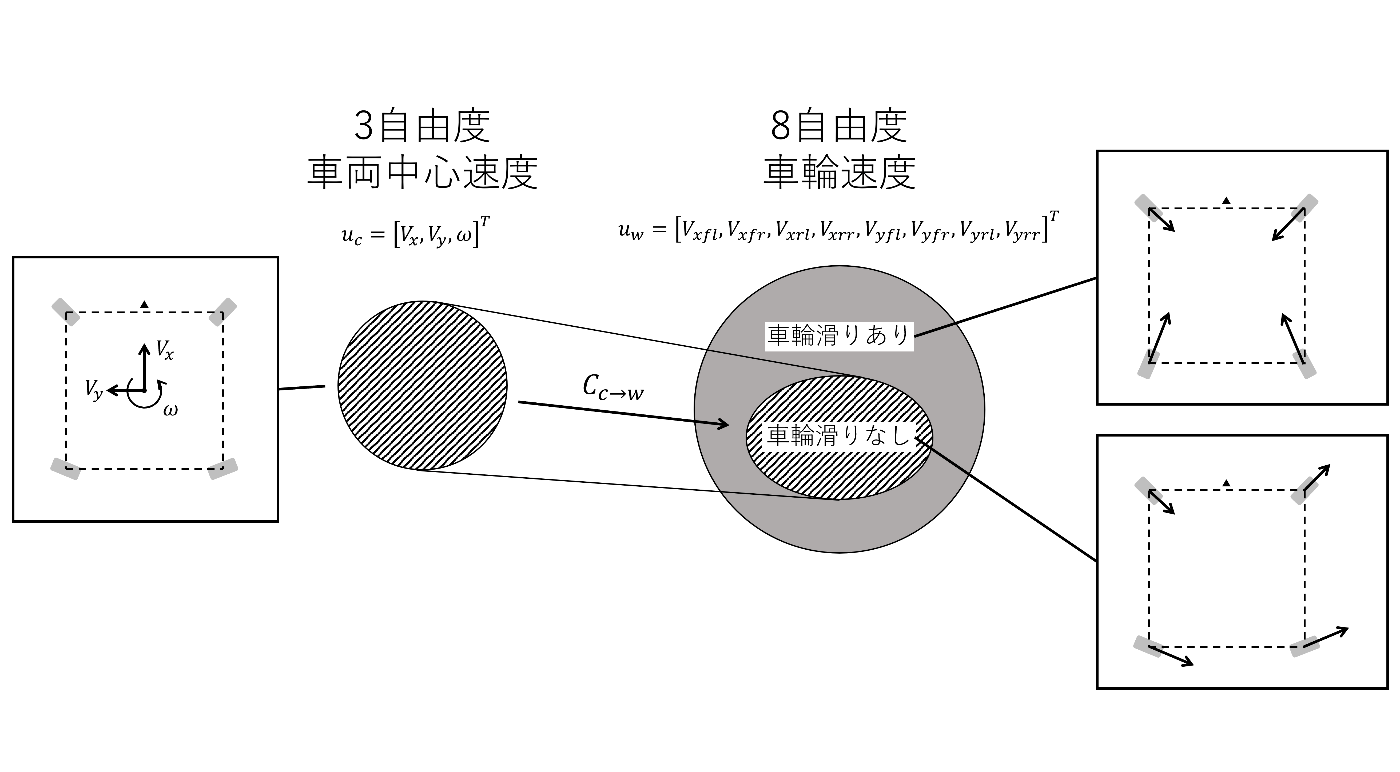
8次元の入力空間\bm{u}_vを探索することは計算量の大きい処理であるだけでなく, もし解が得られたとしても大きな滑りを引き起こし運動を不安定化させる特性を持つ懸念もあります. 代わりに \bm{u}_c を探索した後 \bm{u}_v に変換することで, これらの問題を同時に解決することができます.

車輪滑りなし/あり, それぞれの制御入力空間から適当な値を選んで車両に入力し, 動作を比較してみましょう. 車輪滑りなし(Vehicle Command Without Slip)の入力を用いた場合は地面に接地しつつ動き続けられますが, 車輪滑りあり(Vehicle Command With Slip)の入力を用いた場合は車輪滑りにより生じる地面からの反力を受けて容易に車体が浮いてしまいます.

一方で, 削減した次元を探索する限り「車輪の滑りを利用した車両の挙動」の一切が探索対象から排除されてしまいます. 滑りやすい路面上での走行や極めて高速な走行を行う際には, この限定により車両本来の性能を引き出しきれない可能性がある点に注意が必要です.

まとめると, 3次元の制御入力 \bm{u}_c (車両中心の速度)を探索することは, いくつかの仮定のもとで8次元の車両指令値 \bm{u}_v (4WIDS車両の操舵角・車輪回転速度)を探索することと対応します. MPPIによって3次元の最適な制御入力を求めたら, 式(1)により8次元に変換してから車両への操作指令値として渡せば実際に4WIDS車両の制御が可能です. これで, MPPIの計算に用いる予測モデルが準備できました. 次は評価関数の設計へと進みましょう.

[MPPI適用準備 2/2] 評価関数の設計

本節では, ある制御入力の系列が与えられたとき, その良し悪しを判断するための評価関数を定義しましょう. 時刻tステップの制御入力 \bm{v}_t = [v_x, v_y, \omega]^T , 予測ステップ数 T のときの制御入力系列を \bm{V} = (\bm{v}_0, \bm{v}_1, \cdots, \bm{v}_{T-1}) \in \mathbb{R}^{3 \times T} と表記します. 評価関数 C は \bm{V} を受け取ってスカラーの評価値を返します. 評価値が小さいほど, 引数で受け取った制御入力系列 \bm{V} が引き起こす車両運動がより望ましいものであることを示します.

つまり, 評価関数の設計において行うべきことは, 問題設定の時点でリストアップした要件(安全性, 素早さ, 滑らかさ)を具体的な数式表現に変換し, 望ましい車両運動ほど低い値を返すような表現を見つけることです.

準備: 状態系列の計算

今回, 評価値を計算する際には制御入力の系列だけでなく車両状態の系列が必要になります.
制御入力系列 \bm{V} = (\bm{v}_0, \bm{v}_1, \cdots, \bm{v}_{T-1}) と前節で準備した予測モデル \bm{x}_{t+1} = F(\bm{x}_t, \bm{u}_t) を使ってあらかじめ求めておきましょう.

最新の観測情報から得た車両状態を\bm{x}_0とします. これを予測状態系列の0ステップとして, 与えられた制御入力の系列と予測モデルをもとに状態を繰り返し更新しましょう.

\begin{align*} \bm{x}_1 &= F (\bm{x}_0, \bm{v}_0) \\ \bm{x}_2 &= F (\bm{x}_1, \bm{v}_1) \\ & \vdots \\ \bm{x}_T &= F (\bm{x}_{T-1}, \bm{v}_{T-1}) \end{align*}

すると, 与えられた制御入力系列 \bm{V} = (\bm{v}_0, \bm{v}_1, \cdots, \bm{v}_{T-1}) を入力した場合の車両状態系列 \bm{X} = (\bm{x}_0, \bm{x}_1, \cdots, \bm{x}_{T-1}, \bm{x}_T) が求められました.

安全性の評価

安全性を評価する指標を設計しましょう.
ここでは車両が障害物に衝突しない動作を目指します.
車両状態系列 \bm{X} と障害物の位置情報を準備し, 未来の車両状態が障害物と接触するようならペナルティを追加することにします.

c_{\rm{collision}}(\bm{X}) = \begin{cases} 0 & (\rm{if} \quad \text{no collision}) \\ 1 & (\rm{if} \quad \text{collision}) \end{cases} \quad

素早さの評価

素早さを評価する指標を設計しましょう.
速さと走行経路の2点から評価します.

まず速さについて, ある理想とする速さ v_{\rm{ref}} \in \mathbb{R} を与えたとき, 理想値とできるだけ近い速さを実現するような走行が素早い移動である, という視点で評価します. v_x^k, v_y^kはそれぞれ時刻kステップのx, y方向車両速度入力です.

c_{\rm{speed}}(\bm{V}) = \sum_{k=0}^{T-1} \left[ (v_x^k)^2 + (v_y^k)^2 - (v_{\rm{ref}})^2 \right]

次に走行経路について, 今回のシステムではあらかじめA*によりゴールまでの最短経路が計算されています. この経路に忠実に沿って走る方が素早い移動である, という視点で評価します. つまりは, 経路からずれて走るような挙動にペナルティを加えます. p_x^k, p_y^k, \theta^k はそれぞれ時刻kステップのx, y座標と角度, p_{x}^{\rm{ref}}, p_{y}^{\rm{ref}}, \theta^{\rm{ref}}は追従すべきA*経路上の最近傍点の座標および角度です.

A*経路からの距離偏差について,

c_{\rm{dist}}(\bm{X}) = \sum_{k=0}^{T-1} \left[ (p_x^k - p_{x}^{\rm{ref}})^2 + (p_y^k - p_{y}^{\rm{ref}} )^2 \right],

A*経路からの角度偏差について,

c_{\rm{angle}}(\bm{X}) = \sum_{k=0}^{T-1} (\theta^k - \theta^{\rm{ref}})^2,

とそれぞれ定めました.

滑らかさの評価

滑らかさを評価する指標を設計しましょう.
車両中心速度(3次元)の変化および車両操作入力(8次元)の変化が小さいほど滑らかな走行である, という観点から評価します.

まずは車両中心速度について, 制御入力系列の隣り合う要素同士の差に対してペナルティを追加します.

c_{\rm{smoothc}}(\bm{V}) = \sum_{k=0}^{T-2} \| \bm{v}_{k+1} - \bm{v}_{k} \|_2

次に車両操作入力について, 式(1)により3次元制御入力から8次元車両操作入力へ変換する操作を関数 f_v と表記した上で, 時間変化に対するペナルティを計算します.

c_{\rm{smoothv}}(\bm{V}) = \sum_{k=0}^{T-2} \| f_v(\bm{v}_{k+1}) - f_v(\bm{v}_{k}) \|_2

逆走の防止

上記の評価値設計だけでは, 「A*経路に沿ってゴールから離れる方向へ進む」という行動も望ましいと判断され, 逆走が引き起こされます. これを防ぐため, 予測状態の最終ステップ(Tステップ目)の状態が到達すべきゴールに近いほど望ましい, と判断するための指標を追加しました.

c_{\rm{goal}}(\bm{X}) = (p_x^T - p_{x}^{\rm{goal}})^2 + (p_y^T - p_{y}^{\rm{goal}} )^2

スカラー化

繰り返しになりますが, 評価関数は制御入力系列を受け取り, その評価値をスカラー値として返す必要があります. すなわち, 上で述べた複数の評価値を統合してある一つの代表値に変換してから出力しなければなりません. ここでは重みづけ加算による単純な方法を選択しました.

上で設計した評価指標 c_{\rm{collision}}, c_{\rm{dist}}, c_{\rm{angle}}, c_{\rm{smoothc}}, c_{\rm{smoothv}}, c_{\rm{goal}} それぞれに対する重み定数 w_{\rm{collision}}, w_{\rm{dist}}, w_{\rm{angle}}, w_{\rm{smoothc}}, w_{\rm{smoothv}}, w_{\rm{goal}} を導入すると, 評価関数 C({\bm{V}}) は次のように得られます.

\begin{align*} C({\bm{V}}) = \ &w_{\rm{collision}} c_{\rm{collision}}(\bm{X}) + w_{\rm{dist}}c_{\rm{dist}}(\bm{X}) + w_{\rm{angle}} c_{\rm{angle}}(\bm{X}) + \\ &w_{\rm{smoothc}} c_{\rm{smoothc}}(\bm{V}) + w_{\rm{smoothv}} c_{\rm{smoothv}}(\bm{V}) + w_{\rm{goal}} c_{\rm{goal}}(\bm{X}) \end{align*}

なお, 重み定数は実際に車両を制御した動きを見ながら, 設計者が調整すべきパラメータです.
より重視してほしい評価指標に対する重みを相対的に増加させるような要領で調整します.

モデル予測経路積分制御(MPPI)

予測モデルと評価関数がそろったので, いよいよMPPIを利用する準備ができました.
MPPIの目的は, 評価関数を最小化するような(すなわち最適な)未来の制御入力系列を求めることです. 手法の概要・アルゴリズム・使い方のコツについて順に解説します.

次動画は試しに数種類の制御タスクをMPPIで解いてみた結果です. ソースコードはGithub: MizuhoAOKI/python_simple_mppiで公開しています. 手軽に実装できるわりに良い性能が出ることも多く, なかなか魅力的な手法だと思います.

どんな手法か

MPPIの概要について説明します.

通常, 最適制御問題では, 評価関数を最小化するような制御入力系列そのものを求めようとします. MPPIはこの定式化そのものを見直し, 評価関数が小さいほど確率が高くなるような確率分布(最適制御入力分布)を推定する問題を解く立場をとります.

しかし, 様々な形状を取り得る最適制御入力分布を正確に推定することは非常に難しい問題です. MPPIでは, 正規分布として表現したある制御入力分布を準備し, その分布の平均を最適制御入力分布とうまくフィットするように「ずらす」ことで近似的な推定を達成します.
ちなみに, これは複雑な確率分布を近似的に推定する際に一般的に用いられる変分推論というテクニックです. 変分推論で導入される扱いやすい分布形状のことを変分分布と呼び, MPPIでは正規分布を変分分布として利用します. 正規分布の持つ単峰性・対称性という都合の良い性質のおかげで, 近似的に推定された最適制御入力分布の期待値を求めるだけで, 容易に最適制御入力を得ることができます.

まとめると,

  • 最適制御入力の探索 → 最適制御入力分布の推定, という最適化問題の捉えなおし
  • 変分分布に正規分布を用いた変分推論による最適制御入力分布の推定

の2点が, MPPIという手法の核といえます.

利点・欠点

MPPIの利点・欠点をまとめます.

代表的な特長は, その適用範囲の広さといえるでしょう. 非線形システム・微分不可能な評価関数などにも, 特にアルゴリズムに工夫を加えることなくそのまま適用できます. また, プログラムによる実装も容易です.

一方で, ハード制約を扱いづらかったり, 長期間の未来予測が苦手などの欠点もあります.
MPPIに限らず, サンプリングベースの手法で高次元の空間を探索することは, 必要とされる計算量が膨大となることから根本的に難しい問題です. この問題は「次元の呪い (Curse of Dimensionality)」と呼ばれています.

利点

  • 幅広い制御対象・問題設定に適用可能
  • 実装が容易
  • 素朴なサンプリングベースMPCと比べて, より小さいサンプル数で精度の良い解が得られる

欠点

  • システム状態に関するハード制約を扱いづらい
  • 長期間の未来予測が苦手
  • 最適制御入力分布の多峰性により性能が劣化することがある

MPPIのアルゴリズム

それでは, 以下にMPPIのアルゴリズムを順に説明します. 今回の解説は車両制御を題材にMPPIの処理を具体的にイメージできるように書きました. より一般的かつ詳細な情報はGrady Williams, et al. Information-Theoretic Model Predictive Control: Theory and Applications to Autonomous Drivingをご参照ください.

[Step 1] 制御入力空間におけるサンプリング

制御入力( v_x, v_y, \omega )を先読みする予測ステップ数 T だけ並べた制御入力系列を, 正規分布に従ってサンプリング(乱数を生成)します.

未来予測区間中のある時刻ステップ t \ (t = 0, 1, \cdots, T) について, 正規分布の平均を \bm{u}_t \in \mathbb{R}^3 , 正規分布の共分散行列を \Sigma \in \mathbb{R}^{3 \times 3} とおくと, サンプリングされる制御入力 \bm{v}_t \in \mathbb{R}^3 は次式で表されます.

\bm{v}_t = \bm{u}_t + \bm{\varepsilon}_t, \\ \bm{\varepsilon}_t \sim \mathcal{N}(0, \Sigma).

この処理の結果得られた制御入力系列のサンプルを \bm{V} = (\bm{v}_0, \bm{v}_1, \cdots, \bm{v}_{T-1}) \in \mathbb{R}^{3 \times T}と表記します.

制御入力に上下限制約( \bm{v}_{\rm{min}} \leq \bm{v}_t \leq \bm{v}_{\rm{min}} )を適用したい場合は, ここで値をクリッピングして強制的に制約を満たすようにします.

\begin{align*} \bm{v}_t &= \rm{clamp}( \bm{v}_t, \bm{v}_{\rm{min}}, \bm{v}_{\rm{max}}) \\ &= \min( \max( \bm{v}_t, \bm{v}_{\rm{min}}), \bm{v}_{\rm{max}}) \end{align*}

ここで設定した正規分布は事実上, 解の探索範囲に相当するため, 最適解がありそうな場所に設定すると良い性能が得られます. 実用の際には, 正規分布の共分散行列 \Sigma はあらかじめ定数として与えておき, 分布の平均 \bm{u}_t は前回計算した最適制御入力を用いることが一般的です. この処置は, 制御周期が十分小さい場合, 今回の計算で求める最適制御入力は前回求めた解と大きく変化しないだろう, という推定に基づきます.

具体的にサンプリングの様子をイメージしてみましょう. サンプリングのため, 次図のような正規分布を設定したとします. 図中の予測ステップ数は見やすさのため T=6 と小さく設定しています.

このとき, 1つの制御入力系列をサンプリングすると次図のようになります. 可視化の都合で複数のグラフに分かれていますが, 次図にプロットされているすべての点(3 × 6 = 18個の青い丸)を以て, 18次元の空間における1つの制御入力系列サンプル \bm{V} \in \mathbb{R}^{3 \times T} を表現していることに注意してください.

同様の手順に沿って複数のサンプルを準備します. サンプル数を K とおくと, \bm{V}_k \ (k = {1, \cdots, K}) と表されるK個の制御入力系列を得ることになります. 次図は K=5 の場合の可視化ですが, 実際に十分な性能を発揮するためには, 数百～数千サンプルが必要となることが多いです.

[Step 2] 各サンプルに対する重みの計算

Step 1で得た各サンプルに対する評価値および重みを計算します. このステップでは, ある制御入力系列 \bm{V} \in \mathbb{R}^{3 \times T} の良し悪しをスカラー値で評価する関数 C(\bm{V}) が必要となります. ある制御入力系列に対して評価関数 C(\bm{V}) の返す値が小さいほど, 望ましい車両の動きを実現していることを意味します. 今回の問題設定では, [MPPI適用準備 2/2] 評価関数の設計で準備したものをそのまま利用できます.

MPPIはランダムに生成したサンプルを重みづけ加算することで最適入力を推定しますが, あるサンプルに対する重みは次のように計算されます.

w(\bm{V}) = \frac{1}{\eta} \exp{ \left( {-\frac{1}{\lambda}} \left( C(\bm{V}) + \gamma \sum_{t=0}^{T-1} (\bm{u}_t - \tilde{\bm{u}}_t) \Sigma^{-1} \bm{v}_t - \rho \right) \right)}, \\ \eta = \sum_{k=1}^{K} \exp{ \left( {-\frac{1}{\lambda}} \left( C(\bm{V}) + \gamma \sum_{t=0}^{T-1} (\bm{u}_t - \tilde{\bm{u}}_t) \Sigma^{-1} \bm{v}_t - \rho \right) \right)}, \\ \rho = \min_k \left( C(\bm{V}_k) + \gamma \sum_{t=0}^{T-1} (\bm{u}_t - \tilde{\bm{u}}_t) \Sigma^{-1} \bm{v}_t^k \right).

\lambda, \gammaは定数パラメータ, \eta は全てのサンプル重みの合計が1になるようにする正規化項, \rho はexp計算を数値的に安定して行うために加えるバイアス項です. \tilde{\bm{u}}_t はできるだけ一致すべき制御入力指令値が事前に与えられる場合に用いるノミナル入力と呼ばれるもので, 指令値が与えられない場合は0が設定されます.

数式で書くとやや重く見えるかもしれませんが, 処理そのものは単純です. 各サンプルに対する重み計算の処理を次図に示しました. 図中ではわかりやすさのため \lambda=5.0, \gamma=0.0, \rho=0.0 として計算しています. 評価値の小さい(すなわち, 良い評価の)サンプルには大きい重みが, 評価値の大きい(すなわち, 悪い評価の)サンプルには小さい重みが割り当てられていることがわかります.

ここで, MPPIの持つ実装上の嬉しい特性に触れておきます. 重みを正規化する直前までの処理はサンプル間の計算処理が独立しているため, 並列化による高速実行が可能です.
(参考: C++/Cudaによる高速化例, C++/OpenMPによる高速化例, Python/Pytorchによる高速化例, Python/Jaxによる高速化例)

[Step 3] 最適制御入力系列の計算

サンプルK個の重みづけ平均を取ることで, 最適な制御入力系列 \bm{U}^* を求めます.

\bm{U}^* = \sum_{k=1}^{K} w(\bm{V}_k) \bm{V}_k

この計算で行っていることは, サンプリングに用いた正規分布を最適制御分布にフィットするようずらした後, 分布の期待値(山の頂上部分, 下図参照)を得る, という処理です.

実際に車両制御に用いるときは, \bm{U}^* の1ステップ目のみを使います. 今回は合理的に削減された3次元の状態を探索したので, 実際に車両へ渡す指令値には式(1)で8次元車両操作入力へ変換した値を用います.

なお, 準備: 状態系列の計算で説明した方法により, 最適制御入力系列を適用した場合の車両状態系列を得ることができます. つまりは, 近未来の最適な車両運動の計算結果を可視化できます. 例えば次図のように障害物を回避する動きが達成されているか直感的な確認ができるため, MPPIを実装する上で大きな助けになります.

MPPIの性能を発揮するコツ

MPPIは汎用性の高い手法ですが, いざ適用するとうまくいかないこともよくあります. 例えば, 今回の自律移動システムの開発当初の動きは次動画のようでした. ギクシャクした動きで, 頻繁に壁にぶつかってしまいます. こんなとき, どのような方針で性能を改善すればよいか, 知見をまとめておきます.

MPPIの性能を発揮するために, 手法の限界を正しく知ることが必要です. 経験上, 「最適制御入力分布を正規分布で近似する」という大胆な仮定についての正しい理解が重要です.

MPPIの苦手とする具体的な状況を紹介しましょう.
例えば, 目の前に障害物が存在し, 右に避けても左に避けても通過できる場合, なぜか前進して障害物に突っ込む挙動が出ることがあります(Ex. 1). さらに, 4WIDS車両のように大きな自由度を持つシステムをある目標状態に到達させたいとき, なぜか計算結果が安定せずギクシャクした動作をすることがあります(Ex. 2).
これらの状況に共通するのは, 下図に示す通り, 良い未来を実現する方法が複数存在する点です.

よりMPPIのアルゴリズムに絡めた言い方をすると, 失敗の原因は「最適制御入力分布の多峰性」として理解できます. 簡単のため1次元の制御入力 \bm{u} が評価関数を最小化するような最適値 \bm{u}^* を求める問題について考えましょう.

例えば次図のように最適制御入力分布が単峰性の場合, MPPIは精度よく最適な制御入力を近似することができます. 確率分布の形状は異なっても, 山の頂上部分が一致していれば, 期待値として得られた最適制御入力 \bm{u}^* は評価値(cost)を最小化するものになります.

しかし, 次図のように最適制御入力が多峰性の場合は, 複数の峰を覆うような分布が最適と判定され, 実際には評価の悪い入力を最適であると誤って推定してしまいます. 2つの確率分布の類似度を測る指標としてはKL divergenceが採用されており, この指標の定義そのものも原因の一端を担っています.

この問題の解決方法について, 3つ紹介します.

[方策1] サンプリングの分散 \Sigma を小さくする

根本的解決にはなりませんが, 比較的手軽に行える方策です.
最適制御入力分布が多峰性であっても, 探索範囲を限定して局所的な単峰性分布にフィットすれば, 結果的に制御性能が改善する場合があります. 欠点としては制御入力を大きく変化させるようなキビキビした動きが現れづらくなる点です.

開発当初, 筆者は「分散を大きくしてサンプル数を十分に増やせば一般に良い性能が得られるだろう」と考えておりましたがこれは誤りです. MPPIにおいてサンプル数を増やす方策は確率分布の近似表現を高精度にする効果しか持たず, 多峰性に関する問題の解決に有効ではありません. ご注意ください.

[方策2] 最適制御入力分布が単峰性となるよう問題設定を見直す

MPPIに解かせる問題設定そのものを見直す方策です. 最適制御入力分布が単峰性となる粒度まで分割された問題を解かせれば, MPPIの本領を発揮することができます. 「最適制御入力分布が単峰性である」とは, 評価関数を小さくする動きが複数種類存在しない, という状況であると定性的に理解できます.

今回の自律移動システムにおいて, 「MPPIの探索する次元の削減」, 「A*により計算された最短経路への追従」を行いましたが, これらは最適制御入力分布を単峰性に近づけるための工夫です.

[方策3] MPPIの改良手法の適用を検討する

多峰性の最適制御入力分布への対応は研究され, MPPIの改良手法がいくつか提案されています.
試してみるとより良い性能を得られるケースもあると思います.

改善手法の例を以下に示します. 時系列順に並べました.

実験

シミュレーション環境で実際に自律移動を行った様子を以下に示します.

手動でゴール地点を指定すると, 障害物を避けながら滑らかに移動してくれます.

https://www.youtube.com/watch?v=QTM0OUosf4U

LiDARの点群データからリアルタイムに周辺の障害物を検知するため, 急に出現した障害物を避けて動くことも可能です.

https://www.youtube.com/watch?v=vwcIlWpAevg

実験動画を見ていると, 進行すべき経路が急に変更された際の動作がややぎこちないことに気づきます. 発表した論文(M. Aoki, et al. IROS 2024)では, サンプリングする入力空間を工夫することでこの問題を改善できることを示しました. 改良版の手法(論文中のMPPI-H)は, 本記事で解説した基本的な手法(論文中のMPPI-3D)に比べて, 急な方向転換などを得意とし安全かつ効率的なナビゲーションを達成することができます. 次に動作の様子を示します.

https://www.youtube.com/watch?v=FfVD5FWZdKY

より詳しい内容にご興味がある方は, Project WebsiteやGithub: MizuhoAOKI/mppi_swerve_drive_rosをご覧ください.

さらなる機能の向上について

今回設計した自律移動システムは4WIDS車両のナビゲーションにおいて基本的な性能を有してはいますが, まだまだ改善の余地があります.

例えば, 以下のような改善が考えられます.

  • 安全性について
    • 動的障害物の未来動作を予測して避けたり停止したりする.
  • 素早さについて
    • 車輪摩擦を明示的に扱う車両モデルを準備し, 高速走行に対応する.
  • 滑らかさについて
    • 経路計画だけでなく速度計画も行うことで, スムーズな加減速を実現する.

他にも, 目指すゴール地点や通るべき経路があらかじめ判明しており変更される可能性のない場合は, 毎制御周期にわざわざ最適化問題を解くのではなく, 事前に最適な制御入力の時系列データを準備しておく方針も有効です. 本記事で示した構成はあくまで一例であり, 問題設定に応じて適切な枠組みは変化することにご注意下さい.

[2025/08/23 追記]
ナビゲーション性能を向上した後続の研究成果"Nullspace MPC"をこちらに公開しました. MPPIよりも高速に移動しつつ, より高い安全性を保ちます.ご興味のある方はご覧ください.
https://github.com/MizuhoAOKI/nullspace_mpc

参考文献

最後まで読んで下さった方へのお願い

本記事の内容に誤り, 不正確な表現, 欠けた視点, 追加すべき情報などがあると気づかれた方は, コメントで教えていただけると大変助かります.
この分野に詳しい方のご意見はもちろん, あまり詳しくないけれどここがよくわからなかった, などのコメントも大歓迎です.

Discussion