A+Bから始める異常高速化
この記事は、ComputerScience集会#4 @VRChat 2023-07-18 にて発表したスライドを元にしたものです。
アーカイブ映像: スライド:
競技プログラミング・外典 A+Bから始める異常高速化
～競プロ向け標準入出力周りの高速化研究～
ComputerScience集会#4 @VRChat 2023-07-18
Caution: Unsafe Rust
この発表にはアンセーフなコードを含みます。使用する場合は自己責任でどうぞ。
画像: The Rustonomicon: Meet Safe and Unsafe より
Rust 裏本 (Rustonomicon 日本語訳) https://doc.rust-jp.rs/rust-nomicon-ja/
偉大なる先人は言いました (1)
Rules of Optimization:
ソフトウェア最適化の原則:Rule 1: Don't do it.
第一法則：最適化するな。Rule 2 (for experts only): Don't do it yet.
第二法則（上級者限定）：まだするな。
-- Michael A. Jackson. Principles of Program Design, Academic Press, 1975
-- 鳥居宏次訳, “構造的プログラム設計の原理,” 日本コンピュータ協会, 1980.
偉大なる先人は言いました (2)
Programmers waste enormous amounts of time thinking about, or worrying about, the speed of non critical parts of their programs, and these attempts at efficiency actually have a strong negative impact when debugging and maintenance are considered. We should forget about small efficiencies, say about 97% of the time: premature optimization is the root of all evil.
プログラマーは、プログラムの重要でない部分のスピードについて考えたり、悩んだりすることに膨大な時間を浪費している。そして、こうした効率化の試みは、デバッグやメンテナンスのことを考えると、実際には強い悪影響を及ぼす。小さな効率性、例えば97％程度の効率性については忘れるべきだ：時期尚早の最適化は諸悪の根源である。
Caution: 邪道な高速化の世界へようこそ
競技プログラミングの楽しみ方としては、本質から外れた、実行時間を可能な限り削るための小手先の工夫になります。今回の物も自分の趣味色が強い実装なので、AtCoder上での利用を想定した proconio クレートなどへ取り込まれる事も恐らく無いかと思います。
競技プログラミングの問題の実行時間は、典型的には 2000ms 程度が許されていますが、通常の問題では 10ms 程度の影響も出ることのない範囲です。
逆に、入出力で 0.1ms でもプログラムの実行時間を削りたい人、低レイヤー寄りの高速化に興味のある人は、是非挑戦してみてください。
今回扱う問題は、入出力の量が特に多く、実行時間の入出力部分への影響が比較的大きいものになります。（作問側の想定としても、入出力テストのための問題の一つと位置づけられているようです）
Library Checker: Many A + B (128bit) https://judge.yosupo.jp/problem/many_aplusb_128bit
問題文: この問題は
制約:
( 参考:
入力
T
A B
A B
\ \vdots
A B
出力
A+B
A+B
\ \vdots
A+B
サンプル (上段: 入力サンプル、下段: 出力サンプル)
5
1 2
11 22
-111 -222
10000000000000000000000000000000000000 10000000000000000000000000000000000000
1234567890123456789012345678901234567 -10000000000000000000000000000000000000
3
33
-333
20000000000000000000000000000000000000
-8765432109876543210987654321098765433
CASE 1: 出力回数が多い時に毎回println!すると遅いです : 実行時間 537ms : https://judge.yosupo.jp/submission/149768
println!は毎回OSに出力を行うため、OSくんを50万回呼びつける人状態になります。
use std::io::prelude::*;
fn main() {
let stdin = std::io::stdin();
let mut lines = stdin.lock().lines();
let n = lines.next().unwrap().unwrap().parse::<usize>().unwrap();
for _ in 0..n {
let s = lines.next().unwrap().unwrap();
let mut token = s.split_ascii_whitespace();
let a = token.next().unwrap().parse::<i128>().unwrap();
let b = token.next().unwrap().parse::<i128>().unwrap();
println!("{}", a + b); // 500000回出力するのに毎回println!は…
}
}
CASE 2: 出力回数が多い時は Writeシステムコール呼び出し回数の低減に BufWriter を使いましょう ( proconio クレートの #[fastout] はこれに相当 ) : 実行時間 222ms : https://judge.yosupo.jp/submission/149239
use std::io::prelude::*;
fn main() {
let (stdin, stdout) = (std::io::stdin(), std::io::stdout());
let mut lines = stdin.lock().lines();
let mut writer = std::io::BufWriter::new(stdout.lock()); // 出力バッファ
let n = lines.next().unwrap().unwrap().parse::<usize>().unwrap();
for _ in 0..n {
let s = lines.next().unwrap().unwrap();
let mut token = s.split_ascii_whitespace();
let a = token.next().unwrap().parse::<i128>().unwrap();
let b = token.next().unwrap().parse::<i128>().unwrap();
writeln!(&mut writer, "{}", a + b).unwrap(); // バッファに出力
}
}
どこが高速化できそう?
- 標準入力をバッファ付きで1行ずつ入力している所
- 一度に入力全体を読み込んでから処理できないか？
- 行単位・トークン (空白文字区切り) 単位への分割をしている所
- 入力バイト列が UTF-8 として有効かどうか検査をしている
- 改行文字区切り・空白文字区切りで分割する処理が二重になっている
- 競技プログラミングの入力形式は、通常は改行文字と空白文字をまとめて分割してしまっても問題なく入力できる（トークン数が可変であっても、問題文と最初の入力から入力すべきトークンの数が分かるようになっている）
- トークン文字列から数値にパース（文字データの解析・変換処理）している所
- 文字列→128bit整数 の変換は最大で
1000000
- 文字列→128bit整数 の変換は最大で
- 足し算した結果を文字列にフォーマットしている所
- 128bit整数→文字列 の変換は最大で
500000
- 128bit整数→文字列 の変換は最大で
CASE 3: 一度に全部読み込み、改行と空白文字をまとめて分割 実行時間: 213ms
use std::io::prelude::*;
fn main() {
let (mut stdin, stdout) = (std::io::stdin(), std::io::stdout());
let mut input = String::with_capacity(67_108_864); // 読み込みの格納先
stdin.read_to_string(&mut input).unwrap(); // 一度に読み込み
let mut token = s.split_ascii_whitespace(); // まとめて分割
let mut writer = std::io::BufWriter::new(stdout.lock());
let n = token.next().unwrap().parse::<usize>().unwrap();
for _ in 0..n {
let a = token.next().unwrap().parse::<i128>().unwrap();
let b = token.next().unwrap().parse::<i128>().unwrap();
writeln!(&mut writer, "{}", a + b).unwrap();
}
}
標準入力・標準出力の流れ
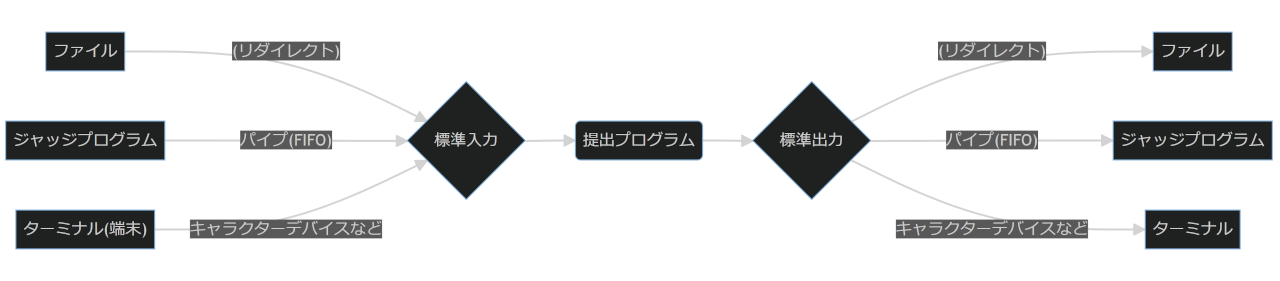
- 通常ジャッジの場合: 入出力:ファイル
- 入力が(書き込み中でない)ファイルだとプログラムの実行開始時点で最後まで読み込める
- 問題がインタラクティブ(対話的)の場合: 入出力:パイプ(FIFO)
- ターミナル(端末)上で実行する場合: 入出力:キャラクターデバイスなど
- パイプ(FIFO)やキャラクタデバイスなどでの入力だと、プログラムの実行開始時点で最後まで読み込める保証が無い
標準入力がファイルかどうかの判定(Linux)
- Linux の fstat システムコール で stat 構造体を取得する
- ファイル種別を示すビットマスク(ソケット/シンボリックリンク/通常のファイル/ブロックデバイス/ディレクトリ/キャラクターデバイス/FIFO(名前付きパイプ))、ファイル種別が通常のファイルであればファイルサイズ、所有権、最終修正時刻など
- Rust の場合、 std::fs::File::from_raw_fd で 標準入力 (File Decscriptor : 0) の Fileオブジェクトを作り、 std::fs::File::metadata を使うとこれらの情報を取得できる
- 2023-06-01 リリースの Rust 1.70.0 では 入出力がターミナル(端末)かどうかを判定する std::io::IsTerminal トレイトが安定化
struct stat {
dev_t st_dev; /* ファイルがあるデバイスの ID */
ino_t st_ino; /* inode 番号 */
mode_t st_mode; /* アクセス保護 (ファイル種別の検査) */
nlink_t st_nlink; /* ハードリンクの数 */
uid_t st_uid; /* 所有者のユーザー ID */
gid_t st_gid; /* 所有者のグループ ID */
dev_t st_rdev; /* デバイス ID (特殊ファイルの場合) */
off_t st_size; /* 全体のサイズ (バイト単位) */
blksize_t st_blksize; /* ファイルシステム I/O でのブロックサイズ */
blkcnt_t st_blocks; /* 割り当てられた 512B のブロック数 */
/* Linux 2.6 以降では、カーネルは以下のタイムスタンプ
フィールドでナノ秒の精度をサポートしている。
Linux 2.6 より前のバージョンでの詳細は NOTES を参照。 */
struct timespec st_atim; /* 最終アクセス時刻 */
struct timespec st_mtim; /* 最終修正時刻 */
struct timespec st_ctim; /* 最終状態変更時刻 */
#define st_atime st_atim.tv_sec /* 後方互換性 */
#define st_mtime st_mtim.tv_sec
#define st_ctime st_ctim.tv_sec
};
read vs mmap
-
read システムコール : ファイルディスクリプターからバッファーに読み込む
- Rust の場合、標準ライブラリではこちらが使われる（Stdin の バッファーサイズは 8192bytes 固定、 40Mbytesの入力に readシステムコール が 約5000回必要）
-
mmap, munmap システムコール : ファイルやデバイスをメモリーにマップ/アンマップする
- 入力がファイルであることを前提に、今回はこちらを使って一括で読み込んでみます
#[must_use]
#[stable(feature = "rust1", since = "1.0.0")]
pub fn stdin() -> Stdin {
static INSTANCE: OnceLock<Mutex<BufReader<StdinRaw>>> = OnceLock::new();
Stdin {
inner: INSTANCE.get_or_init(|| { // stdio::STDIN_BUF_SIZE は 8192bytes で固定
Mutex::new(BufReader::with_capacity(stdio::STDIN_BUF_SIZE, stdin_raw()))
}),
}
}
CASE 4: mmapを使用 : 実行時間 191ms : https://judge.yosupo.jp/submission/149279
#![cfg(target_os = "linux")]
use std::io::prelude::*;
fn solve(s: &str) {
let stdout = std::io::stdout();
let mut token = s.split_ascii_whitespace();
let mut writer = std::io::BufWriter::new(stdout.lock());
let n = token.next().unwrap().parse::<usize>().unwrap();
for _ in 0..n {
let a = token.next().unwrap().parse::<i128>().unwrap();
let b = token.next().unwrap().parse::<i128>().unwrap();
writeln!(&mut writer, "{}", a + b).unwrap();
}
}
fn main() {
unsafe {
use std::os::unix::io::FromRawFd;
// unsafe: 標準入力 (file discriptor 0) の metadata を取得 (内部で fstat システムコール)
match std::fs::File::from_raw_fd(0).metadata() {
Ok(metadata) if metadata.is_file() => { // 入力がファイルだった時の処理
let filelen = metadata.len(); // ファイルサイズ
// unsafe: mmap システムコール にてファイルをメモリマップドアクセス
let input = mmap(std::ptr::null_mut(), filelen as usize, 1, 2, 0, 0);
// unsafe: UTF-8 の有効性チェックを省略、 &[u8] を &str に強制キャスト
solve(std::str::from_utf8_unchecked(std::slice::from_raw_parts(
input,
filelen as usize,
)));
}
_ => panic!(), // panic: このサンプルでは、入力がファイルでなかった時の実装は省略
}
}
}
// unsafe: FFI
// (foreign function interface)
// Linux C Library (libc)
#[link(name = "c")]
extern "C" {
pub fn mmap(
addr: *mut u8,
length: usize,
prot: i32,
flags: i32,
fd: i32,
off: isize,
) -> *mut u8;
}
入力がファイル以外だった時のアプローチ
Rust では std::io::BufRead トレイトに fill_buf (バッファが空なら充填して取得できた領域を返す、空でなければ使っていない領域を返す), consume (fill_buf で受け取った領域からどれだけ消費したかを BufRead に伝えて後の fill_buf で消費済みの領域が再び戻ってこないようにする) という比較的低レベルな機能があるので、これを使って実装する方法があります。
今回は時間の関係で、こちらのアプローチの詳細は省略します。
use std::io;
use std::io::prelude::*;
let stdin = io::stdin();
let mut stdin = stdin.lock();
let buffer = stdin.fill_buf().unwrap();
// work with buffer
// バッファを消費する
println!("{buffer:?}");
// ensure the bytes we worked with aren't returned again later
// 消費したバイト列の領域が、また後で fill_buf によって戻ってこないようにする
let length = buffer.len();
stdin.consume(length);
文字列 → 128bit整数への変換ですが…
これは10000個の非負整数が書かれた文字列を128bit整数へ変換するベンチマークですが…
何と、Rustでは 初期値0 から 文字列を左から順番に見ていって 10倍してから その桁の数字を足す という処理を繰り返した方が約2倍速かったりします。 (測定環境: AMD Zen+)
str::parse::<u128>()
722,148 ns/iter (+/- 6,374)
bench.iter(|| -> Vec<u128> {
values
.iter()
.map(|s| s.parse::<u128>().unwrap())
.collect::<Vec<_>>()
});
文字列先頭から1文字ずつ処理:
370,237 ns/iter (+/- 6,918)
bench.iter(|| -> Vec<u128> {
values
.iter()
.map(|s| {
s.as_bytes()
.iter()
.fold(0u128, |p, &c| p * 10 + ((c - b'0') as u128))
})
.collect::<Vec<_>>()
});
何故 Rust の parse は遅い? (推測)
- その文字列が本当にその数値型に正常に収まる数値が書かれているか検査しながら変換しているので遅い。
- 今回は、入力された文字列が制約通りであると仮定し、検査処理を省略して 文字列→整数 のパースを実装してみます
- 10進数の文字列を変換するのに特化せず、任意の基数の文字列を変換できるよう汎化しているため。
- 10進数が書かれた文字列の処理に特化させて最適化を図ってみます
エンディアン (endianness) / バイト順 (byte order)
図: ASCII文字列 "endianness⏎" の先頭8byteの領域を、それぞれのエンディアンで8byte整数として読み込んだ値の16進数表記
2bytes 幅以上の数値をコンピュータ上のメモリに格納する時や、データとして転送する時に、最下位のbyte (LSB: Least Significant Bit/Byte) から順番に格納や転送を行うことを リトルエンディアン (little-endian) と言います。逆に、最上位のbyte (MSB: Most Significant Bit/Byte) から順番に行うものは ビッグエンディアン (big-endian) と言います。
Intel/AMD x86_64 アーキテクチャでは、主にこのリトルエンディアンが使われています。
ビッグエンディアン は、例えば インターネット上での通信プロトコル、 TCP/IP のヘッダ部分で数値をエンコーディングするのに使われます（ネットワークバイトオーダー）。 TCP/IP のペイロード部分のエンディアンはアプリケーションの実装次第で異なります。
8byte長の文字列を64bit整数に分割統治法で変換(1)
まずは、例として "12345678" の文字列を リトルエンディアン の 64bit整数型 に読み込んでみます。
まずは読み込んだ64ビット整数を8ビット区切りで考え、左は最上位バイト(MSB)、右は最下位バイト(LSB)とします。表内の () 内の数字は上の16進数を10進数にした値です。
- 先頭の
"1"の文字は最下位バイト(LSB)に、末尾の"8"の文字は最上位バイト(MSB)に読み込まれます。 - 64bit整数
0x0F0F0F0F0F0F0F0Fと AND演算 をして不要な所をマスクし、各桁毎の数を取り出します。 - 整数
0xA01(10進数で2561) を掛け算します。2桁ごとに区切った数が現れています。2^{8}\times 10^1+1=2561 - 8bit の 右シフト演算 をして、2桁ごとにまとめた値の位置を調整します。
-
0x00FF00FF00FF00FFとの AND演算 をして、 不要な桁にマスクを掛けます。
| MSB | LSB | 処理 | ||||||
|---|---|---|---|---|---|---|---|---|
0x38(56)"8"
|
0x37(55)"7"
|
0x36(54)"6"
|
0x35(53)"5"
|
0x34(52)"4"
|
0x33(51)"3"
|
0x32(50)"2"
|
0x31(49)"1"
|
u64::from_le_bytes |
0x08(8)
|
0x07(7)
|
0x06(6)
|
0x05(5)
|
0x04(4)
|
0x03(3)
|
0x02(2)
|
0x01(1)
|
AND 0x0F0F0F0F0F0F0F0F |
0x4E(78)
|
0x43(67)
|
0x38(56)
|
0x2D(45)
|
0x22(34)
|
0x17(23)
|
0x0C(12)
|
0x01(1)
|
× 0x0000000000000A01 |
0x00(0)
|
0x4E(78)
|
0x43(67)
|
0x38(56)
|
0x2D(45)
|
0x22(34)
|
0x17(23)
|
0x0C(12)
|
>> 8 |
0x00(0)
|
0x4E(78)
|
0x00(0)
|
0x38(56)
|
0x00(0)
|
0x22(34)
|
0x00(0)
|
0x0C(12)
|
AND 0x00FF00FF00FF00FF |
8byte長の文字列を64bit整数に分割統治法で変換(2)
次は、16bit区切りの値に注目して処理していきます。
- 整数
0x640001(10進数で6553601) を掛け算2^{16}\times 10^2+1=6553601
- 16ビット右シフト
-
0x0000FFFF0000FFFFとの AND演算
をします。
| MSB | LSB | 処理 | ||
|---|---|---|---|---|
0x3837"78"
|
0x3635"56"
|
0x3433"34"
|
0x3231"12"
|
u64::from_le_bytes |
0x0807 |
0x0605 |
0x0403 |
0x0201 |
AND 0x0F0F0F0F0F0F0F0F |
0x4E43 |
0x382D |
0x2217 |
0x0C01 |
× 0x0000000000000A01 |
0x004E |
0x4338 |
0x2D22 |
0x170C |
>> 8 |
0x004E(78)
|
0x0038(56)
|
0x0022(34)
|
0x000C(12)
|
AND 0x00FF00FF00FF00FF |
0x162E(5678)
|
0x0D80(3456)
|
0x04D2(1234)
|
0x000C(12)
|
× 0x0000000000640001 |
0x0000(0)
|
0x162E(5678)
|
0x0D80(3456)
|
0x04D2(1234)
|
>> 16 |
0x0000(0)
|
0x162E(5678)
|
0x0000(0)
|
0x04D2(1234)
|
AND 0x0000FFFF0000FFFF |
8byte長の文字列を64bit整数に分割統治法で変換(3)
最後に 32bit 区切りで見ていきます。
- 整数
0x271000000001(10進数で42949672960001) を掛け算2^{32}\times 10^4+1=42949672960001
- 32ビット右シフト
をします。これで完成です。
| MSB | LSB | 処理 |
|---|---|---|
0x38373635"5678"
|
0x34333231"1234"
|
u64::from_le_bytes |
0x08070605 |
0x04030201 |
AND 0x0F0F0F0F0F0F0F0F |
0x4E43382D |
0x22170C01 |
× 0x0000000000000A01 |
0x004E4338 |
0x2D22170C |
>> 8 |
0x004E0038 |
0x0022000C |
AND 0x00FF00FF00FF00FF |
0x162E0D80 |
0x04D2000C |
× 0x0000000000640001 |
0x0000162E |
0x0D8004D2 |
>> 16 |
0x0000162E(5678)
|
0x000004D2(1234)
|
AND 0x0000FFFF0000FFFF |
0x00BC614E(12345678)
|
0x000004D2(1234)
|
× 0x0000271000000001 |
0x00000000(0)
|
0x00BC614E(12345678)
|
>> 32 |
8byte長の文字列を64bit整数に分割統治法で変換(4)
Rust でのコードにすると、このような感じになります。
fn parseuint_raw8b(s: [u8; 8]) -> u64 {
(((((u64::from_le_bytes(s) & 0x0f0f0f0f0f0f0f0f)
.wrapping_mul((10 << 8) + 1) >> 8) & 0x00ff00ff00ff00ff)
.wrapping_mul((100 << 16) + 1) >> 16) & 0x0000ffff0000ffff)
.wrapping_mul((10000 << 32) + 1) >> 32
}
| 符号なし整数10000個のparse | 32bit整数(~10桁) | 64bit整数(~20桁) | 128bit整数(~39桁) |
|---|---|---|---|
str::parse::<u128>().unwrap() str::parse::<u64>().unwrap() str::parse::<u32>().unwrap()
|
117,630 ns/iter (+/- 1,631) |
238,559 ns/iter (+/- 2,310) |
720,681 ns/iter (+/- 16,091) |
| 文字列先頭から1文字ずつ | 65,094 ns/iter (+/- 717) |
131,462 ns/iter (+/- 1,320) |
364,676 ns/iter (+/- 4,186) |
| 分割統治法で8文字ずつ | 32,570 ns/iter (+/- 420) |
56,551 ns/iter (+/- 637) |
94,753 ns/iter (+/- 568) |
8byte長の文字列を64bit整数に分割統治法で変換(5)
x86_64 アセンブラに変換した後の結果はこのような感じになります。
レジスタ代入が4回、掛け算が3回、AND演算が3回、右シフト演算が3回で処理できている事が見て取れます。
これと同様の手法は、SIMDレジスタを用いてもっと長い区切りで並列的に処理することもできます。
fn parseuint_raw8b(s: [u8; 8]) -> u64 {
(((((u64::from_le_bytes(s) & 0x0f0f0f0f0f0f0f0f)
.wrapping_mul((10 << 8) + 1) >> 8) & 0x00ff00ff00ff00ff)
.wrapping_mul((100 << 16) + 1) >> 16) & 0x0000ffff0000ffff)
.wrapping_mul((10000 << 32) + 1) >> 32
}
parseuint_raw8b:
movabs rax, 1085102592571150095 # 0x0F0F0F0F0F0F0F0F
and rax, rdi # AND演算
imul rax, rax, 2561 # × 0xA01
shr rax, 8 # 右8ビットシフト
movabs rcx, 71777214294589695 # 0x00FF00FF00FF00FF
and rcx, rax # AND演算
imul rax, rcx, 6553601 # × 0x640001
shr rax, 16 # 右16ビットシフト
movabs rcx, 281470681808895 # 0x0000FFFF0000FFFF
and rcx, rax # AND演算
movabs rax, 42949672960001 # 0x0000271000000001
imul rax, rcx # 掛け算
shr rax, 32 # 右32ビットシフト
ret # return
(リトルエンディアン(le)・ビッグエンディアン(be)向けの文字列→整数変換用のヘルパー関数の実装の一部)
pub fn parseuint_arith8le(a: u64) -> u64 {
(((((a & 0x0f0f0f0f0f0f0f0f).wrapping_mul((10 << 8) + 1) >> 8) & 0x00ff00ff00ff00ff)
.wrapping_mul((100 << 16) + 1)
>> 16)
& 0x0000ffff0000ffff)
.wrapping_mul((1_0000 << 32) + 1)
>> 32
}
pub fn parseuint_arith8be(a: u64) -> u64 {
(((((a & 0x0f0f0f0f0f0f0f0f).wrapping_mul((1 << 8) + 10) >> 8) & 0x00ff00ff00ff00ff)
.wrapping_mul((1 << 16) + 100)
>> 16)
& 0x0000ffff0000ffff)
.wrapping_mul((1 << 32) + 1_0000)
>> 32
}
pub fn parseuint_arith4le(a: u32) -> u32 {
(((a & 0x0f0f0f0f).wrapping_mul((10 << 8) + 1) >> 8) & 0x00ff00ff).wrapping_mul((100 << 16) + 1)
>> 16
}
pub fn parseuint_arith4be(a: u32) -> u32 {
(((a & 0x0f0f0f0f).wrapping_mul((1 << 8) + 10) >> 8) & 0x00ff00ff).wrapping_mul((1 << 16) + 100)
>> 16
}
pub fn parseuint_arith2le(a: u16) -> u16 {
(a & 0x0f0f).wrapping_mul((10 << 8) + 1) >> 8
}
pub fn parseuint_arith2be(a: u16) -> u16 {
(a & 0x0f0f).wrapping_mul((1 << 8) + 10) >> 8
}
pub fn parseuint_arith1(a: u8) -> u8 {
a & 0x0f
}
128bit整数から文字列への変換(1)
0000 ～ 9999 までの
__udivti3 が使われる: 比較的遅い）ので、手動で最適化します。
128bit整数から文字列への変換(2)
128bit(最大
fn divrem_1e32(x: u128) -> (u32, u128) {
// (y0, y1) = (floor(x / 10^32), x mod 10^32)
// floor((2^128)/(10^32)) = 3402823
let mut y0 = ((((x >> 64) as u64 as u128) * 3402823) >> 64) as u32;
let mut y1 = x - (y0 as u128) * 1_0000_0000_0000_0000_0000_0000_0000_0000;
if let Some(yt) = y1.checked_sub(1_0000_0000_0000_0000_0000_0000_0000_0000) {
y1 = yt;
y0 += 1;
}
(y0, y1)
}
128bit整数から文字列への変換(3)
fn divrem_1e16(x: u128) -> (u64, u64) {
debug_assert!(x < 1_0000_0000_0000_0000_0000_0000_0000_0000);
// (z0, z1) = (floor(x / 10^16), x mod 10^16)
// floor((2^107)/(10^16)) = 16225927682921336
let mut z0 = ((((x >> 43) as u64 as u128) * 16225927682921336) >> 64) as u64;
let mut z1 = (x - (z0 as u128) * 1_0000_0000_0000_0000) as u64;
if let Some(zt) = z1.checked_sub(1_0000_0000_0000_0000) {
z1 = zt;
z0 += 1;
}
(z0, z1)
}
128bit整数から文字列への変換(4)
通常の除算を使用した場合のアセンブラ出力例:
汎用的な128bit除算のソフトウェア実装 __udivti3 を呼び出していたり、レジスタの使用量が多く、 push / pop が発生していたりするのが見て取れます。
const D32U: u128 = 100000000000000000000000000000000;
pub fn divrem_1e32_std(x: u128) -> (u32, u128) {
let y0 = (x / D32U) as u32;
let y1 = x % D32U;
(y0, y1)
}
divrem_1e32_std:
push r15
push r14
push r12
push rbx
push rax
mov rbx, rsi
mov r14, rdi
movabs r15, -8814407033341083648
movabs r12, 5421010862427
mov rdx, r15
mov rcx, r12
call qword ptr [rip + __udivti3@GOTPCREL]
mov rcx, rax
mov rsi, rdx
imul r12, rax
mov rax, rcx
mul r15
add rdx, r12
imul rsi, r15
add rsi, rdx
sub r14, rax
sbb rbx, rsi
mov eax, ecx
mov rdx, r14
mov rcx, rbx
add rsp, 8
pop rbx
pop r12
pop r14
pop r15
ret
128bit整数から文字列への変換(5)
__udivti3 の呼び出しが排除され、レジスタの使用量が減っているのが見て取れます。
const D32U: u128 = 100000000000000000000000000000000;
pub fn divrem_1e32(x: u128) -> (u32, u128) {
// (y0, y1) = (floor(x / 10^32), x mod 10^32)
// floor((2^128)/(10^32)) = 3402823
let mut y0 = ((((x >> 64) as u64 as u128) * 3402823) >> 64) as u32;
let mut y1 = x - (y0 as u128) * D32U;
if let Some(yt) = y1.checked_sub(D32U) {
y1 = yt;
y0 += 1;
}
(y0, y1)
}
divrem_1e32:
mov r8, rsi
mov ecx, 3402823
mov rax, rsi
mul rcx
mov rsi, rdx
movabs rcx, -5421010862428
mov r10, rdx
imul r10, rcx
movabs r9, 8814407033341083648
mov rax, rdx
mul r9
add r10, rdx
add rax, rdi
adc r10, r8
add r9, rax
adc rcx, r10
movabs rdx, -8814407033341083649
cmp rdx, rax
movabs rdx, 5421010862427
sbb rdx, r10
cmovae rcx, r10
cmovae r9, rax
adc esi, 0
mov eax, esi
mov rdx, r9
ret
128bit整数から文字列への変換(6)
ベンチマーク結果:
- 縦軸: 1出力あたりの所要時間(単位:ナノ秒)
- 横軸: 出力する数の10進数での桁数
- 青線: Rustの標準フォーマッタによる出力(128bit整数)
- 黄線: Rustの標準フォーマッタによる出力(64bit整数)
- 赤線: 今回の実装(128bit整数)
- 緑線: 今回の実装(64bit整数)
let c_std = || -> String {
let mut s = String::with_capacity(N * 40);
for &e in values.iter() {
use std::fmt::Write;
write!(&mut s, "{}", e).unwrap(); // 標準のフォーマッタによる出力
s.push(' '); // 空白文字区切り、write!内のフォーマット文字列に空白文字加えるより、こちらのが速い
}
s
};
let c_lib = || -> String {
let mut s = String::with_capacity(N * 40);
let v = unsafe { s.as_mut_vec() };
let r = v.as_mut_ptr();
let mut p = r;
for &e in values.iter() {
unsafe {
dec4le.rawbytes_u128(&mut p, e); // 今回作成した出力ルーチンを呼び出し
*p = b' '; // 空白文字区切り
p = p.add(1);
}
}
unsafe { v.set_len((p as usize) - (r as usize)) };
s
};
std版参考: Qiita: Rustで数値を連結した文字列を作るときはItertools::joinが速い
補足: 除算の最適化の例 (1/6)
除数・被除数がある程度小さい場合 :
例:
補足: 除算の最適化の例 (2/6)
例: 64bit環境で
pub fn udiv3(x: u64) -> u64 {
x / 3
}
pub fn udiv3_shim(x: u64) -> u64 { // 上の関数と同じ最適化がされる関数
((x as u128) * (((1u128 << 65) - 1) / 3 + 1) >> 65) as u64
}
pub fn udiv1e8(x: u64) -> u64 {
x / 100000000
}
pub fn udiv1e8_shim(a: u64) -> u64 { // 上の関数と同じ最適化がされる関数
((x as u128) * (((1u128 << 90) - 1) / 100000000 + 1) >> 90) as u64
}
補足: 除算の最適化の例 (3/6)
例: 64bit環境で
最後の変形は、
pub fn udiv7(x: u64) -> u64 {
x / 7
}
pub fn udiv7_shim(x: u64) -> u64 { // 上の関数と同じ最適化がされる関数
let t = ((x as u128) * (((1u128 << 67) - 1) / 7 + 1 - (1u128 << 64)) >> 64) as u64;
(((x - t) >> 1) + t) >> 2
}
補足: 除算の最適化の例 (4/6)
例:
// 10^24 未満の整数 x の入力に対して floor(x / 10^16), (x mod 10^16) を計算
// ceil(2^115 / 10^16) = ceil(2^99 / 5^16) = 4153837486827862103
// 0 <= x < 10^24 < 2^80
// --> floor(floor(x / 2^16) * ceil(2^115 / 10^16) / 2^99) = floor(x / 10^16)
pub fn udivrem1e16_less1e24(x: u128) -> (u64, u64) {
debug_assert!(x < 1000000000000000000000000);
let y1 = (((x >> 16) as u64 as u128) * 4153837486827862103 >> 99) as u64;
let y0 = (x - (y1 as u128) * 10000000000000000) as u64;
(y1, y0)
}
pub fn udiv3(x: u64) -> u64 {
x / 3
}
pub fn udiv3_shim(x: u64) -> u64 { // 上の関数と同じ最適化がされる関数
((x as u128) * (((1u128 << 65) - 1) / 3 + 1) >> 65) as u64
}
# x86_64-unknown-linux-gnu
udiv3:
mov rax, rdi
movabs rcx, -6148914691236517205
mul rcx
mov rax, rdx
shr rax
ret
# aarch64-unknown-linux-gnu
udiv3:
mov x8, #-6148914691236517206
movk x8, #43691
umulh x8, x0, x8
lsr x0, x8, #1
ret
pub fn udiv1e8(x: u64) -> u64 {
x / 100000000
}
pub fn udiv1e8_shim(a: u64) -> u64 { // 上の関数と同じ最適化がされる関数
((x as u128) * (((1u128 << 90) - 1) / 100000000 + 1) >> 90) as u64
}
# x86_64-unknown-linux-gnu
udiv1e8:
mov rax, rdi
movabs rcx, -6067343680855748867
mul rcx
mov rax, rdx
shr rax, 26
ret
# aarch64-unknown-linux-gnu
udiv1e8:
mov x8, #52989
movk x8, #33889, lsl #16
movk x8, #30481, lsl #32
movk x8, #43980, lsl #48
umulh x8, x0, x8
lsr x0, x8, #26
ret
pub fn udiv7(x: u64) -> u64 {
x / 7
}
pub fn udiv7_shim(x: u64) -> u64 { // 上の関数と同じ最適化がされる関数
let t = ((x as u128) * (((1u128 << 67) - 1) / 7 + 1 - (1u128 << 64)) >> 64) as u64;
(((x - t) >> 1) + t) >> 2
}
# x86_64-unknown-linux-gnu
udiv7:
movabs rcx, 2635249153387078803
mov rax, rdi
mul rcx
sub rdi, rdx
shr rdi
lea rax, [rdi + rdx]
shr rax, 2
ret
# aarch64-unknown-linux-gnu
udiv7:
mov x8, #9363
movk x8, #37449, lsl #16
movk x8, #18724, lsl #32
movk x8, #9362, lsl #48
umulh x8, x0, x8
sub x9, x0, x8
add x8, x8, x9, lsr #1
lsr x0, x8, #2
ret
// 10^24 未満の整数 x の入力に対して floor(x / 10^16), (x mod 10^16) を計算
pub fn udivrem1e16_less1e24(x: u128) -> (u64, u64) {
// must be x < 10^24
debug_assert!(x < 1000000000000000000000000);
// (z0, z1) = (floor(x / 10^16), x mod 10^16)
// ceil(2^115 / 10^16) = ceil(2^99 / 5^16) = 4153837486827862103
let z0 = (((x >> 16) as u64 as u128) * 4153837486827862103 >> 99) as u64;
let z1 = (x - (z0 as u128) * 10000000000000000) as u64;
(z0, z1)
}
# x86_64-unknown-linux-gnu
udivrem1e16_less1e24:
mov rax, rsi
shld rax, rdi, 48
movabs rcx, 4153837486827862103
mul rcx
mov rax, rdx
shr rax, 35
movabs rdx, -10000000000000000
imul rdx, rax
add rdx, rdi
ret
# aarch64-unknown-linux-gnu
udivrem1e16_less1e24:
mov x9, #30807
extr x8, x1, x0, #16
movk x9, #45331, lsl #16
movk x9, #25903, lsl #32
movk x9, #14757, lsl #48
umulh x8, x8, x9
mov x9, #2420047872
movk x9, #30989, lsl #32
lsr x8, x8, #35
movk x9, #65500, lsl #48
madd x1, x8, x9, x0
mov x0, x8
ret
補足: 除算の最適化の例 (5/6)
乗算の桁数が大きすぎる場合 ( 今回
(
(
補足: 除算の最適化の例 (6/6)
前頁: (
// 2^128 未満の整数 x の入力に対して floor(x / 10^32), (x mod 10^32) を計算
pub fn udivrem_1e32(x: u128) -> (u64, u128) {
// (z0, z1) = (floor(x / 10^32), x mod 10^32)
// floor((2^128)/(10^32)) = 3402823
let mut z0 = ((((x >> 64) as u64 as u128) * 3402823) >> 64) as u64;
let mut z1 = (x - (z0 as u128) * 100000000000000000000000000000000);
if let Some(zt) = z1.checked_sub(100000000000000000000000000000000) {
z1 = zt;
z0 += 1;
}
(z0, z1)
}
# x86_64-unknown-linux-gnu
udivrem_1e32:
mov ecx, 3402823
mov rax, rsi
mul rcx
mov r8, rdx
movabs rcx, -5421010862428
mov r10, rdx
imul r10, rcx
movabs r9, 8814407033341083648
mov rax, rdx
mul r9
add r10, rdx
add rax, rdi
adc r10, rsi
add r9, rax
adc rcx, r10
movabs rdx, -8814407033341083649
cmp rdx, rax
movabs rdx, 5421010862427
sbb rdx, r10
cmovae rcx, r10
cmovae r9, rax
adc r8, 0
mov rax, r8
mov rdx, r9
ret
# aarch64-unknown-linux-gnu
udivrem_1e32:
mov w8, #60487
mov x9, #18137646891008
movk w8, #51, lsl #16
movk x9, #31315, lsl #48
mov x10, #-16732
mov x13, #-18137646891009
umulh x8, x1, x8
movk x10, #53906, lsl #16
movk x10, #64273, lsl #32
mov x14, #16731
movk x13, #34220, lsl #48
movk x14, #11629, lsl #16
umulh x11, x8, x9
movk x14, #1262, lsl #32
mul x12, x8, x9
madd x11, x8, x10, x11
adds x12, x12, x0
adc x11, x11, x1
adds x9, x12, x9
adc x10, x11, x10
cmp x13, x12
sbcs xzr, x14, x11
cinc x0, x8, lo
csel x2, x10, x11, lo
csel x1, x9, x12, lo
ret
// 10^32 未満の整数 x の入力に対して floor(x / 10^16), (x mod 10^16) を計算
pub fn udivrem_1e16_less1e32(x: u128) -> (u64, u64) {
// must be x < 10^32
debug_assert!(x < 100000000000000000000000000000000);
// (z0, z1) = (floor(x / 10^16), x mod 10^16)
// floor((2^107)/(10^16)) = 16225927682921336
let mut z0 = ((((x >> 43) as u64 as u128) * 16225927682921336) >> 64) as u64;
let mut z1 = (x - (z0 as u128) * 10000000000000000) as u64;
if let Some(zt) = z1.checked_sub(10000000000000000) {
z1 = zt;
z0 += 1;
}
(z0, z1)
}
# x86_64-unknown-linux-gnu
udivrem_1e16:
mov rax, rsi
shld rax, rdi, 21
movabs rcx, 16225927682921336
mul rcx
movabs rcx, -10000000000000000
mov rsi, rdx
imul rsi, rcx
add rsi, rdi
add rcx, rsi
movabs rdi, 9999999999999999
xor eax, eax
cmp rsi, rdi
seta al
cmovbe rcx, rsi
add rax, rdx
mov rdx, rcx
ret
# aarch64-unknown-linux-gnu
udivrem_1e16:
mov x9, #4984
extr x8, x1, x0, #43
movk x9, #12209, lsl #16
mov x11, #-2420047873
movk x9, #42341, lsl #32
movk x11, #34546, lsl #32
movk x9, #57, lsl #48
movk x11, #35, lsl #48
umulh x8, x8, x9
mov x9, #2420047872
movk x9, #30989, lsl #32
movk x9, #65500, lsl #48
madd x10, x8, x9, x0
add x9, x10, x9
cmp x10, x11
csel x1, x9, x10, hi
cinc x0, x8, hi
ret
全部やった結果・まとめ
- CASE 1: 毎回println: 実行時間 537ms : https://judge.yosupo.jp/submission/149768
- CASE 2: BufWrite使用: 実行時間 222ms : https://judge.yosupo.jp/submission/149239
- CASE 3: 一度に読み込む: 実行時間 213ms : https://judge.yosupo.jp/submission/149269
- CASE 4: mmap使用: 実行時間 191ms : https://judge.yosupo.jp/submission/149279
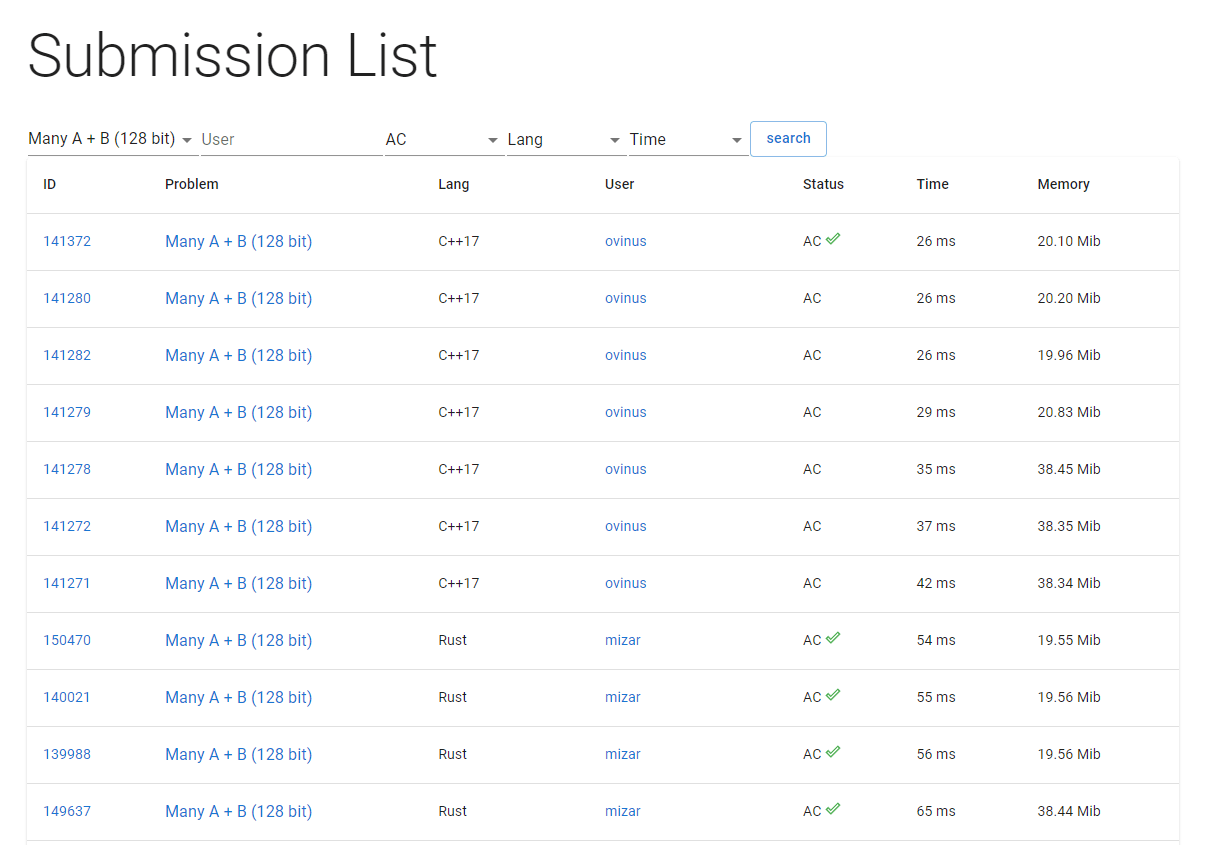
- CASE 5: 整数入出力の改善など: 実行時間 54ms : https://judge.yosupo.jp/submission/150470
この図は、CASE5の提出結果とそのソースコードを表示したページのスクリーンショットです。
もっと速い実装
Many A + B (128bit) では半分の私の実装よりも半分の実行時間な投稿もあります。
こちらは入出力に10進数↔2進数の基数変換を用いず、10進数のままで加減算を行うという物なので、方向性は私の実装とはかなり異なるものです。
Fastest Submissions
まとめ
- Rust は標準で何でもかんでも速いわけじゃない
- エラーチェックや汎用化の都合などで、専用に最適化したものより遅い事も
- Rust は安全に書くこともできる言語ですが、敢えてそれを踏み外す事もできる
- FFI (foreign function interface)、インラインアセンブラ、生ポインタ、etc.
- 注意深く使えば、 unsafe な部分の悪影響を極小化しつつ、いろいろできる…かも?
- 異常高速化の世界へようこそ!
- でも、不要不急の高速化を無理に試みなくても大丈夫です。たぶん。
参考資料・関連資料 (1)
- 「ハッカーのたのしみ―本物のプログラマはいかにして問題を解くか」 ヘンリー・Ｓ・ウォーレン、ジュニア
定数による除算に関する議論も含めた、さまざまな基本的な演算に対する深掘りを論じている本です。
- 「乗算を用いた不変整数による除算」 Torbjörn Granlund and Peter L. Montgomery. 1994. Division by invariant integers using multiplication. SIGPLAN Not. 29, 6 (June 1994), 61–72.
- 「Parsing series of integers with SIMD」 Wojciech Muła
さらに進んで、複数の数値文字列を同時にSIMDでパースする方法について論じています。
- 「CPU/GPU高速化セミナー 浮動小数点から文字列への高速変換の論文を読んでみた / cpugpu acceleration seminar 20230201」 株式会社フィックスターズ
今記事では対象外ですが、浮動小数点から文字列への高速変換 Ryu https://github.com/ulfjack/ryu の解説や、その後登場した Dragonbox https://github.com/jk-jeon/dragonbox について触れられています。
参考資料・関連資料 (2)
今回は使用していませんが、このような実装も存在するという紹介です。
- 文字列→float (C++) : https://github.com/fastfloat/fast_float
- float→文字列 (C++) : https://github.com/jk-jeon/dragonbox
- 文字列→int (Rust) : https://github.com/pacman82/atoi-rs
- int→文字列 (Rust) : https://github.com/dtolnay/itoa
- 文字列→float (Rust) : https://github.com/aldanor/fast-float-rust
- float→文字列 (Rust) : https://github.com/dtolnay/dragonbox
- 除算/剰余算の特殊化アルゴリズム (Rust) : https://github.com/AaronKutch/specialized-div-rem
VRC競プロ部 案内
- 主に土曜23時頃~ (AtCoder Beginner Contest (ABC) 開催日) ABC感想会
- AtCoder Beginner Contest にリアルタイムで参加した人たちで集まって、 Group+ インスタンスにてわいわいと感想会をやっています。初めての方は Discord / VRChat Group に参加しておいた方がスムーズだと思います。
- https://discord.gg/VDQMrAb
- https://vrc.group/PROCON.7592
- 主に日曜夜 (コンテストがない週): テーマ別勉強会
- 2023-06開催 SECCON Beginners CTF 2023 に
VRC-proconチームで参加 (20位)
VRC競プロ部 コンテスト
2023-07-21(金)21:20 ~ 23:20 yukicoder にて
私は A 問題のWriterとして作問に参加しました。
解くだけではなく、問題や解説を見るだけでも、皆さんに楽しんで頂けたらと思います。
Discussion