SVGをBoneアニメーションさせるためのtransform概論
前置き
世界人口70億人のうちの3人くらいに需要があると言われているかもしれないSVGをBoneアニメーションさせるためのtransform技術概論。
これは1つの方針方法であり、必ずしも正解かつ最適というわけではない。
3人のうちの1人(自分)は残念ながら先人の資料を見つけられなかったので、いつか現れるであろう残る2人が別のもっと効率的かつシンプルな素晴らしい方法を見つけてくれることを願いつつここに資料を残す。ついでに自分用のメモでもある。
ここに記した方針を実装に落としたソフトウェアの紹介はこちら。
ざっと眺めてもらえれば最終的に何を目的としているかは見えてくるはず。
またBoneについてはBlenderのそれを多く参考にしている。
editモードとposeモードという概念もBlenderからそのまま拝借していて、もしBlenderに知見があるのならそれを念頭に置きながら読み進めると理解が早い。
Boneの変形
Boneのeditモードとposeモード
editモード
Boneのheadと

tailの位置を編集するためのモードをeditモードと呼んでいる。

headとtailはそれぞれ任意の座標を指定することができる。

アニメーションさせたいSVG要素に合わせてBoneを配置していくためのモードと考えることもできる。
続くposeモードでBoneを変形させたときに、editモードにおける位置関係が維持されるようにSVG要素を変形することが最終的な目的である。
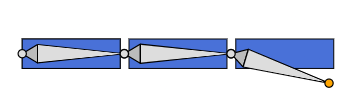
poseモード
editモードで配置したBoneを基準として、追加の変形を加えるためのモードをposeモードと呼んでいる。
例えばeditモードではこういう状態のBoneが、

poseモードではこういう状態になっていたとする。
この場合は、Boneのheadとtailの位置が変化したわけではなく、Bone自体がtranslate変形されたと解釈する。

もしeditモードでも上のようにずれた状態のままであったとしたら、それはBoneのheadとtailが最初からそこに配置されていて、Bone自体は何も変形されていないと解釈できる。
poseモードで加えた各種変形をキーフレームとして保存し、キーフレーム間を補完することでアニメーションを表現することが可能になる。
Boneのtransfrom
データ構造上は親子関係を形成しているが、最終的なBoneのtransformはそれぞれ独立した変形として算出している。
このtransformとBone本来(editモード時)の配置を組み合わせてBoneをレンダリングする。
また大前提としてBoneのtransformは、Bone本来の配置におけるheadからtailに向かうベクトルをy軸、そこから-90度回転したベクトルをx軸としたBoneのlocal空間における変形を表現している。
つまりeditモードでBoneをどのように配置したかによってtransfromの軸も変化する。

Boneとそのtransformのデータ型はこのようになっている。
interface Vector2 {
x: number
y: number
}
interface Transform {
translate: Vector2
rotate: number
scale: Vector2
}
interface Bone {
id: string
head: Vector2
tail: Vector2
transform: Transform
}
Affine変換の移動(translate)、回転(rotate)、拡大縮小(scale)の3要素を1つのtransformとしてまとめている。
ちなみに今回はAffine変換のもう1つの要素である剪断(skew)は変形として考慮に入れていない。アニメーションの表現としてあまり使わなさそうだったので省いただけで大きな理由はない。おそらく剪断を考慮に入れたとしても変形操作の大枠に変化はないはず。いつか取り入れるかもしれない。
translateの軸
繰り返すがtransformはBoneのlocal空間における変形を表している。
もしBoneに親となるBoneが存在する場合、親Boneの変形はそのまま子Boneのlocal空間にも適用される。
例えばこのように2つのBoneが親子関係を持っているとして、

子Boneをx軸方向に-30ほどtranslateするとこうなる。親Boneが変形されていないので子Boneのlocal空間そのままのxy軸で移動している。

ここでさらに親を回転すると、このような状態になることを期待したい。

このとき子Boneは親の変形に沿って位置が変わっただけで、自身のtransformは何も変化していない。つまりx軸に沿ってtranslateしたままの状態になっている。
親Boneが回転したことで、子Boneが属する空間(parent空間)が回転し、移動軸であったx軸も回転したと考えれば辻褄が合う。
rotateの挙動
Boneのlocal空間における回転を表しているので、Bone本来(editモード時)の配置からheadを基点とした回転を表している。
scaleの軸
scaleもtranslateと同じくBoneのlocal空間における変形となっている。変形の基点はrotateと同じくBoneのheadである。

例えばscaleのxを増やしたとすると、Boneはこのように変形する。

同様にscaleのyを増やすとこのように変形する。

この変形はBoneのlocal空間に対してのものなので、Boneを回転させたとしてもその形状は保たれる。

transformのorigin
すでに触れていたが、Boneアニメーションを自然に表現するにはrotateとscale変形をBoneのheadを原点として行うことが求められる。
Boneとは文字通り骨なので、関節であるheadを基点に回転したり拡大縮小したり(現実世界の骨では考えにくいが)してくれなければ困ったことになる。
しかしAffine変形は通常であれば空間の原点を回転や拡大縮小の基点とするため、そのままではBoneのheadを基点とした変形とは一致しない。このずれを解消するためにheadの位置が変形の基点となるような調整を挟み込む必要がある。
Affine変形の算出
transformのデータ型はこれで必要十分なものの、この表現のままではBoneを意図した通りに変形することはまだできない。
なぜならこのtransformはeditモードで配置したBoneに対するlocal空間な変形を表現しているだけで、実際にBoneを変形してレンダリングするにはSVG空間(global空間)における変形表現が必要となるからである。
headが原点のままなら変形もシンプルで、translate(x, y) rotate(r) scale(x y)という順番で変形を使えばよい。
rotateとscaleは順不同だがtranslateは左端(最後に適用するのと同義)にする必要がある。もしrotate translateという順番になっていると、translateの軸がrotateによって変形され、Boneのlocal空間からずれてしまう。
一方で原点以外の座標がheadに指定されているケースが厄介で、rotateとscaleをhead基準で行うための補助的な変形を行う必要が出てくる。
難しそうな雰囲気を醸し出したがやること自体は意外とシンプルで、最初にheadが原点となるよう移動し、最後にその移動を元に戻せばよい。つまりこのような行列の並びを用意する。
[
translate(head.x, head.y),
translate(translate.x, translate.y),
rotate(r),
scale(scale.x, scale.y),
translate(-head.x, -head.y),
]
Boneの傾き
次にBoneの相対的な変形をSVG空間における絶対的な変形に置き換えることを考える。
Boneのlocal空間とSVG空間にはずれが生じているので、そのずれを一旦解消し、Boneのtransformを適用し、再度そのずれを元に戻せばよい。

つまり、local空間の軸がglobal空間の軸と一致するように回して、transformを適用して、先ほどの回転を元に戻したい。

Bone自体の傾き(headからtailに向かうベクトルの角度)をbrとしておく。brが0のときBoneのtailはglobal空間のx軸に向かっている。
local空間においてtailの方向はy軸であるので、さらに90度回転すればBoneのlocal空間とglobal空間の軸が一致したことになる。

青色がglobal軸、赤色がlocal軸を表している。見やすさのためにずらしているが、実際は原点で重なっている。
以上を踏まえてBoneのtransform変形の前後でその傾きのリセットと再適用を行うためにはこのような行列の並びを用意すればよい。headの位置を調整したのと同じ手順である。
[
translate(head.x, head.y),
rotate(br - 90),
translate(translate.x, translate.y),
rotate(r),
scale(scale.x, scale.y),
rotate(-br + 90),
translate(-head.x, -head.y),
]
ついにBoneのtransformを得ることができた。
あとはそれぞれの変形をAffine変形m(a, b, c, d, e, f)で書き直し、その積を求めればBoneのglobal空間におけるAffine変形を得ることができる。
Boneの親子関係
やっとBoneのAffine変形を得ることができたが、Boneであるが故に解決しなければならない事項がまだ残っている。
親子関係である。手は腕に、腕は胴体に、Boneは他のBoneと繋がっているからこそBoneなのである。
アニメーション表現においてBoneはtree構造で表現されることが多い。子は単独の親を持ち、親は複数の子を持つ。今回もそれに倣って親子関係を表現する。
子が単独の親を持つということで、Boneに親への参照情報を追加しておく。
子の順番は特に考慮しないのでindexのような情報は持たせていない。
もし親への参照を持っていなかった場合、そのBoneはtreeのroot要素と解釈できる。rootは複数存在することもあるが、rootが異なればtreeとしても独立しているのでそれぞれ個別に考えていくだけでよい。
interface Bone {
id: string
head: Vector2
tail: Vector2
transform: Transform
parentId?: string
}
Boneの親子関係とSVGの親子関係
なぜ親子関係を解決したAffineを得る必要があるかを補足すると、Boneの親子関係とSVGの親子関係は独立した存在であり、親子関係が残ったままのBoneをSVG側で扱うことは非常に難しいからである。
例えば腕を作るとして、Boneはこのように綺麗な階層で組んだとする。
- 胴体
- 二の腕
- 肘先
- 手
一方でSVGがそれと同じ構造で作られているとは限らない。SVGの<g>タグによる階層化は骨組みを意識して使うことは稀で、グラフィックの作りやすさや取り回しやすさのための単なるグルーピングとして使われていることがほとんどである。
場合によっては全く階層を作らずフラットに全ての要素を用意することもできる。
- 胴体
- 二の腕
- 肘先
- 手

このとき肘先と手をBoneとSVG要素とでそれぞれ対応させてみたとする。
Bone側では肘先の子として手が紐ついているので、肘先のBoneを回転したら手のBoneも合わせて回転する。

このとき手のBone自身は(そのlocal空間において)何も変形されていない。
そしてSVG側の手はSVG側の肘先とは何の関係もないので、手のBoneによるAffine変形のみが適用される。よって上図のように手のSVG要素はその場に置いていかれる結果となる。
しかし実際には我々は下図のように手のBoneと手のSVG要素の位置は常に一致していることを願っている。Boneの親子関係がどうなっていようと、SVGの親子構造がどうなっていようと、対応つけたBoneとSVG要素の見た目の位置が一致していてくれることを願っている。
もしそうなっていなければ、目に見えるものだけを信じず、内部のデータ構造を把握した上で動きをエミュレートする相当の能力が要求されるだろう。そのようなソフトウェアは人類には早すぎる。

既に説明がややこしくなってきていることも分かるようにBoneとSVGの親子構造を同時に考慮することは非常に難しい。そして残念ながら両方の親子構造を考慮しなければ上記のような見た目通りの変形を実現することはできない。
ならばせめて、Bone側ではBoneだけの、SVG側ではSVGだけの親子関係を考えればいいような状況を作りたい。
そこでBoneのAffine変形をSVG側に受け渡す前準備として、Boneの親子関係をすべて解決し、それぞれ独立したBoneがAffine変形を持っているだけという状態まで情報を加工する。
親子関係を解決したAffine変形
親子関係を解決した子BoneのAffine変形を得るだけであればやることはシンプルで、親BoneのAffine変形(親子関係解決済)を子Boneのtransformから算出したAffine変形に左から適用すればよい。
親子関係を解決した子BoneのAffine = 親子関係を解決した親BoneのAffine x 子BoneのAffine
root要素には親がいないことが保証されているのでroot要素から下っていけば演繹的に全てのBoneの親子関係を解決したAffine変形を得ることができる。
SVG要素変形に必要なもの
SVG要素を変形するために必要な情報をBoneそれぞれのAffine変形に集約したため、以降ではBoneのheadや親子関係などに関する情報は必要なくなる。
単にどのBoneがどのAffine変形を持っているかという情報だけ知っていればよい。
type Affine = [number, number, number, number, number, number]
interface BoneAffineMap {
[id: string]: Affine
}
SVG要素の変形
Boneとのバインド
SVG要素はそれぞれ1つのBoneとバインドすることができる。バインドされたBoneの変形をSVG要素側に自然な形で反映することが最終的な目的である。
Boneの情報は既にAffine行列へ加工されているものとして考えていく。
type Affine = [number, number, number, number, number, number]
interface BoneAffineMap {
[id: string]: Affine
}
シンプルなケース
変形対象となるSVG要素にtransform属性がなく、<g>タグによる階層構造にも属していなければ最もシンプルなケースに該当する。
このケースではバインドしたBoneのAffine行列をそのままtransform属性にセットするだけでよい。
<rect transform="matrix(BoneのAffine行列)" />
SVGがtransformを持つケース
RB = matrix(BoneのAffine行列)
RE = matrix(rect要素のAffine行列)
SVG要素自体のAffine行列に、BoneのAffine行列を左からかけると目的の変形が得られる。
先にSVG本来の座標変換をしてからBoneによる座標変換を重ねていると考えれば理にかなった順序である。
<rect transform="RB RE" />
これからより複雑なケースになったとしても、「先にSVG本来の座標変換をしてからBoneによる座標変換を重ねる」が原則となる。SVG本来の座標変形とはそのSVGを形成するための先天的な変形であり、Boneによる変形とは先天的な変形が行われたうえでの後天的な変形なのである。
この原則を崩さないような変形行列の並べ方を見つけることで最終目的は達成される。
<g>タグがtransformを持つケース
SVGは<g>タグを用いることで要素をグルーピングすることができる。XML形式なのでグルーピングとは階層構造のことを指している。そしてこの階層構造が、Bone変形を行う際の非常に厄介な存在となる。
元々のSVGがこのようになっているとする。<rect>がREという変形を持っている。
RE = matrix(rect要素のAffine行列)
<g>
<rect transform="RE" />
</g>
ここで、<g>がGEという変形を持っていたとする。
GE = matrix(g要素のAffine行列)
<g transform="GE">
<rect transform="RE" />
</g>
この状態からさらに、<rect>にRBというBone変形をかけたいケースを考える。
RB = matrix(rect要素のBoneのAffine行列)
まずはシンプルに考えてこうしてみる。しかしこれはうまくいかない。
<g transform="GE">
<rect transform="RB RE" />
</g>
なぜうまくいかないかというと、最もシンプルなケースでは成立していた「SVG要素自体のAffine行列に、BoneのAffine行列を左から掛ける」という形式が崩れてしまっているからである。
SVG要素自体のAffine行列とはroot要素からその要素までにかかる全てのAffine行列の積であり、このケースではGE REのことを指している。
GE REという変形が<rect>にかかることでオリジナルのSVGとしてのグラフィクスがまず表現される。そこへさらにRGという変形を重ねるのだから、RB GE REという変形が最終的に<rect>要素に掛かることを期待しているのである。
先程の変形だと<rect>要素にかかる最終的な変形はGE RB REであり、要素自体のAffine行列の隙間にBoneのAffine行列が挟まるという奇妙な形になってしまっている。
行列の積に交換法則は成り立たないので、よほどの条件が揃っていなければこの変形はRB GE REとは一致しない。
それでは「SVG要素自体のAffine行列に、BoneのAffine行列を左からかける」を保てばよいのだからと、こういう形を試してみる。
<g transform="RB GE">
<rect transform="RE" />
</g>
確かに<rect>にかかる最終的な変形行列はRB GE REとなっている。
一見成功に見えるが実は罠があり、この方法だと<g>タグに属す他の無関係な要素にも変形がかかってしまう。
例えば下のような状況だと<rect>の変形は確かに狙い通りだが、<circle>には最終的にRB GBという意図しない変形がかかってしまっている。本来であれば<circle>にかけるべき最終的な変形はGEのはずである。この形式でも狙った変形にはまだ届かないようである。
<g transform="RB GE">
<rect transform="RE" />
<circle />
</g>
この問題を回避するには<g>のtransformは何も変更せず、<rect>のtransformだけを変更してRB GE REという変形行列の並びを得る必要がある。
みんな大好き逆行列の登場である。X^-1はXの逆行列と認識して欲しい。
そして<rect>のtransformをこのように並べてみる。
<g transform="GE">
<rect transform="GE^-1 RB GE RE" />
<circle />
</g>
最終的に<rect>にかかる変形行列はGE GE^-1 RB GE RE、つまりRB GE REとなるので目的の変換行列が無事に得られている。
そして<circle>にかかる最終的な変形行列はGEのままであり、こちらも期待通りの形となっている。
ちなみにGE^-1が存在しない場合はAffine行列の性質的にGEがscaleを0にするような変形になっているので、この要素自体を描画する必要がなくなる。
場合分けしてmatrix(0, 0, 0, 0, 0, 0)を入れてしまえばよい。
<g>タグにBoneのtransformがかかるケース
GB = matrix(g要素のBoneのAffine行列)
下記の状態から、<g>にはGBを、<rect>にはRBというBone変形を行いたいというケースを考える。
<g transform="GE">
<rect transform="RE" />
<circle />
</g>
まずは<g>タグにBoneの変形を加える。
<g transform="GB GE">
<rect transform="RE" />
<circle />
</g>
Affine行列の積はAffine行列であることを利用してGB GEの逆行列を臆せず利用し、<g>タグがtransformを持つケースと同じくこのように行列を並べる。
前述のように逆行列が存在しない場合は要素自体を描画する必要がなくなるので別途場合分けする。
<g transform="GB GE">
<rect transform="GE^-1 GB^-1 RB GE RE" />
<circle />
</g>
最終的な変形行列はRB GB GE REではなくRB GE REなことに注意。
つまりGBは<rect>要素には影響を与えていない。
再び腕の例で考えてみる。
Bone側がこのような親子関係を持っていたする。手のBoneが親を持たず浮いた状態になっている。
- 胴体
- 二の腕
- 肘先
- 手
SVG側は素直にこのような構造になっているとする。
- 胴体
- 二の腕
- 肘先
- 手
そしてBoneとSVG要素を名前の通り素直にバインドしておく。

このとき肘先を動かしたら、次のように変形されることを期待しているはずである。
SVG側では手は肘先の子要素であるが、バインドされた手のBoneは何も変形されていないので、親である肘先要素の変形を無視するかのようにその場に留まっている。
親である肘先要素には当然ながら肘先BoneのAffine変形が適用されているので、通常であれば子である手要素にもその変形の影響は波及する。つまりここではその影響、肘先BoneのAffine変形を打ち消すことが求められている。

この打ち消しを実現するのがGE^-1 GB^-1 RB GE REという行列の並びである。
仮にGBとRBの元になったBoneが親子関係を持っていたとしても、そのときはRBには既にGBの変形も含まれていることになる。なぜならBoneの親子関係を解決した状態のAffine変形を求めたのだから。
つまりBone側で親子関係があろうとなかろうと、この行列の並びによってSVG側の親子関係を解決することが可能である。
多段階層の一般ケース
段々とややこしくなってきたが要するにターゲット要素にかかる最終的な変換行列が、その要素の根元からの本来のAffine行列に、その要素のBoneのAffine行列を左からかける並びになっていれば目的の変形が達成される。
子要素の変形行列を得るには親要素の変形行列が必要となるので、SVGの根元から先端に向かって階層を下りながら各要素のtransformを解決していくという計算手順となる。
例えばこのような多段にネストされた<rect>にRBというBoneのAffine行列をかけたいとしたら、
<g transform="GE1">
<g transform="GE2">
<rect transform="RE" />
<circle />
</g>
</g>
最終的にRB GE1 GE2 REという変形行列を並べたいのでこのような形にすればよい。
ターゲット要素のtransformを変更しているだけなので、<circle>には影響を及ぼす心配もない。
<g transform="GE1">
<g transform="GE2">
<rect transform="GE2^-1 GE1^-1 RB GE1 GE2 RE" />
<circle />
</g>
</g>
さらに親要素にもBoneの変形GB1とGB2がかかっていたのなら、最終形は次のようになる。一見複雑だが同じ操作を親から子に向かって順番に繰り返しているだけである。
<g transform="GB1 GE1"> <!-- => GB1 GE1 -->
<g transform="(GB1 GE1)^-1 GB2 GE1 GE2"> <!-- => GB2 GE1 GE2 -->
<rect transform="(GB2 GE1 GE2)^-1 RB GE1 GE2 RE" /> <!-- => RB GE1 GE2 RE -->
<circle />
</g>
</g>
その要素の根元からのAffine行列に、その要素のBoneのAffine行列を左からかける並びが最終的に常に実現されていることを確認して欲しい。
ここまでくれば、あとはどれだけ深い親子構造であったとしても同じ操作を繰り返すことで全ての要素に対する変形行列を得ることができる。
以上によって、SVGをBoneアニメーションさせるためのtransformを得るという目的は達成された。
Discussion