機械学習における損失関数とは

損失関数とは

定義と基本概念

損失関数（Loss Function）とは，機械学習モデルが予測した値と実際の正解値との間の差異を定量的に評価するための関数です．簡単に言うと，モデルの予測の「誤差」を測る指標であり，損失関数の値が小さいほど，モデルの予測が正確であることを意味します．損失関数は，モデルの学習プロセスにおいて，どの方向にパラメータを更新すべきかを示す羅針盤のような役割を果たします．

損失関数の具体例

平均二乗誤差（MSE）

平均二乗誤差は，予測値と実際の値との誤差の二乗の平均を計算したものです．
数式で表すと以下のようになります．

$$MSE = \frac{1}{n} \sum^{n}_{i=1} (y_i - \hat{y}_i)^2$$

ここで，$n$はデータポイントの総数，$y_i$は実際の値（真の値），$\hat{y}_i$はモデルによる予測値です．
MSEが損失関数として採用される主な理由として
（１）誤差を二乗することで，大きな誤差に対してより大きなペナルティを与えることができること
（２）滑らかかつ微分可能なため勾配降下法などの最適化アルゴリズムに適応しやすいこと
などが挙げられます．

平均絶対誤差（MAE）

平均絶対誤差は，予測値と実際の値との誤差の絶対値の平均を計算したものです．数式で表すと以下のようになります．

$$MAE = \frac{1}{n} \sum^{n}_{i=1} \| y_i - \hat{y}_i \|$$

MAEが損失関数として採用される主な理由として
（１）MSEと比較して大きな誤差（外れ値）の影響を小さくできること
（２）誤差の平均値が元の同じデータの同じ単位になるため，直感的な解釈がしやすいこと
などが挙げられます．

最適化アルゴリズムと損失関数

「機械学習モデルの学習」を勾配降下法などの最適化アルゴリズムで行う場合，「機械学習モデルの学習」とは「損失関数の最小化を目指して機械学習モデルに用いるパラメータ（重みやバイアス）を調整すること」を意味します．
以下では，シンプルな線形回帰モデルについて「機械学習モデルの学習」について具体例を示します．

モデルの決定

線形回帰モデル

$$\hat{y}_i = w x_i + b$$

ここで，$w$は重み（パラメータの一つ），$x_i$は入力データ，$b$はバイアス（パラメータの一つ），$\hat{y}_i$は入力$x_i$に対するモデルの予測値です．

損失関数の設定

ここでは，平均二乗誤差（MSE）を採用します．また，損失関数（Loss Function）の頭文字を取って簡易的に（後で出てくる偏微分の記号を見やすくするために）全体を$L$と表記します．

$$L = \frac{1}{n} \sum^{n}_{i=1} (y_i - \hat{y}_i)^2 = \frac{1}{n} \sum^{n}_{i=1} (y_i - (w x_i + b))^2$$

パラメータの更新

ここでは，勾配降下法を採用します．損失関数の最小化のために，損失関数$L$について，パラメータ$w$に関する勾配$\frac{\partial L}{\partial w}$と，パラメータ$b$に関する勾配$\frac{\partial L}{\partial b}$を求め，$w$と$b$を更新していきます．

$$w \leftarrow w - \eta \frac{\partial L}{\partial w} \\ b \leftarrow b - \eta \frac{\partial L}{\partial b}$$

ここで，$\eta$は学習率（Learning Rate）と呼ばれる，「各パラメータの勾配の影響をどれほどにするのか」を決めるパラメータであり，コードの実装の際には具体的な数値を人間が決めます．$\eta$を大きくすれば早く学習が進むのではないか？と思われるかもしれませんが，$\eta$が大きくなると最適解を飛び越えてしまい，損失関数が上手く機能しなくなる可能性があります．とはいえ，$\eta$を小さくしすぎると学習に時間がかかりすぎたり，本当は最小値に到達したいのに極小値から抜け出せなくなったりするので$\eta$を決める際には注意が必要です．

import numpy as np
import matplotlib.pyplot as plt

# 1. データセットの作成
# ランダムシードを設定して結果の再現性を確保
np.random.seed(20)

# 入力データ（例として0から2までの範囲で100個のランダムな値）
X = 2 * np.random.rand(100, 1)

# 実際のターゲット値（例として線形関数にノイズを加えたもの）
# 真の関係式：y = 4 + 3x + ノイズ
y = 4 + 3 * X + np.random.randn(100, 1)

# 2. パラメータの初期化
# 重み（w）とバイアス（b）をランダムな値で初期化→学習で最適化を目指す
w = np.random.randn(1)
b = np.random.randn(1)

# 3. 学習率とエポック数の設定
learning_rate = 0.1  # 学習率
epochs = 50          # エポック数（学習の繰り返し回数）

# 損失関数の履歴を記録するリスト
loss_history = []

# 4. 勾配降下法による学習ループ
for epoch in range(epochs):
    # 4.1 予測値の計算
    # 現在のパラメータを使用して予測を行う
    y_pred = w * X + b

    # 4.2 損失関数の計算（平均二乗誤差：MSE）
    # 各データポイントの誤差の二乗を平均化
    loss = np.mean((y - y_pred) ** 2)
    loss_history.append(loss)  # 損失をリストに記録

    # 4.3 勾配の計算
    # 損失関数を重みとバイアスで微分して勾配を求める
    dw = -2 * np.mean(X * (y - y_pred))  # 重みに関する勾配
    db = -2 * np.mean(y - y_pred)        # バイアスに関する勾配

    # 4.4 パラメータの更新
    # 勾配と学習率を使ってパラメータを更新
    w = w - learning_rate * dw
    b = b - learning_rate * db

    # 4.5 進捗の表示
    # 10エポックごとに損失とパラメータの値を表示
    if (epoch + 1) % 10 == 0:
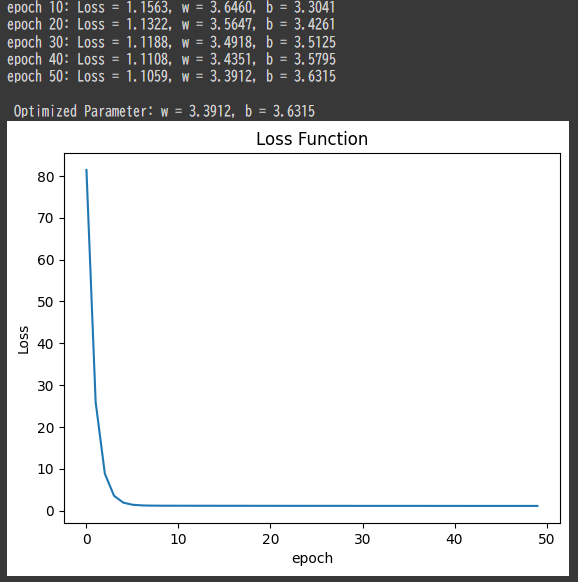
        print(f"epoch {epoch+1}: Loss = {loss:.4f}, w = {w[0]:.4f}, b = {b[0]:.4f}")

# 5. 学習結果の表示
# 最終的な重みとバイアスの値を表示
print(f"\n Optimized Parameter: w = {w[0]:.4f}, b = {b[0]:.4f}")

# 6. 損失関数の推移をプロット
# 学習過程での損失の変化をグラフ化
plt.plot(range(epochs), loss_history)
plt.xlabel('epoch')
plt.ylabel('Loss')
plt.title('Loss Function')
plt.show()

上記のコードを実行すると以下の出力がされました．エポック数（学習の繰り返し回数）が増加すると損失関数が減少する，というのが理想です．

実は知識よりも忍耐力が必要だったり，，，

LIfE iS Like a Boat