Transform2Dが示すものはなにか

Transform2Dとは

みんな大好きTransform2Dノードとはコレである。

みんながしっている挙動

ことあるごとに使うこの基本ノードだが、入力した角度やスケールがいちいちリセットしてしまい「結局今何度回転させたのか？何倍に拡縮したのか？」わからなくなることがないだろうか？

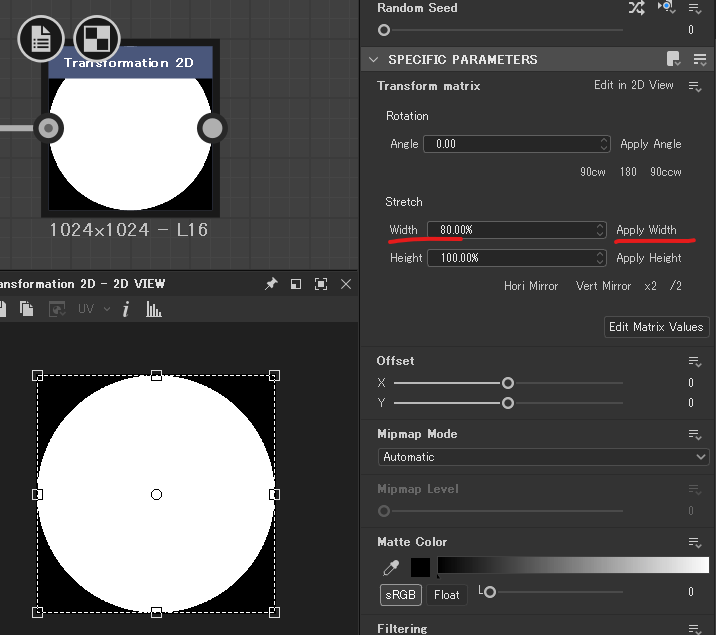
Widthを設定してApplyを２回押すと…

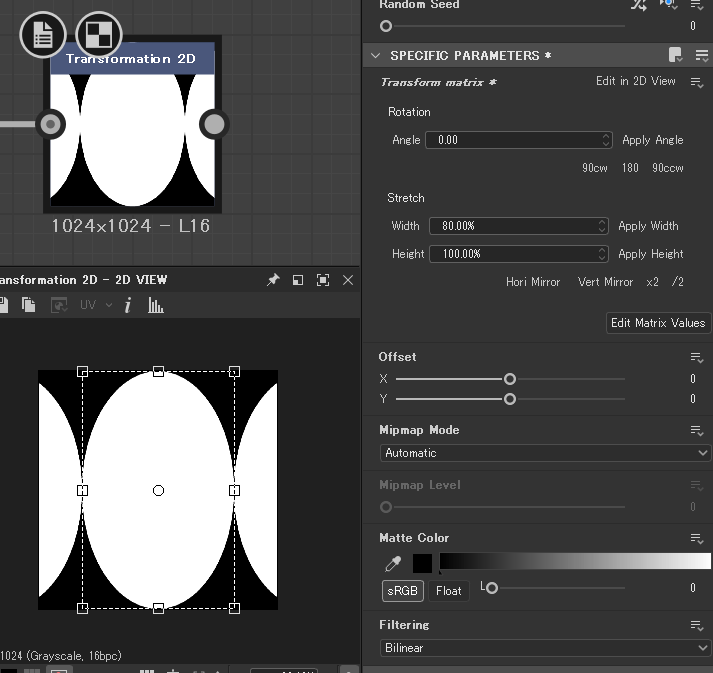
幅が0.8倍の0.8倍になる
この挙動の何が面倒かというと、最初、80%の大きさにしていたものを60%に変更したい場合に、ただ単に60%でApplyすればいいというものではないのだ。

Edit Matrix Value

では、入力した値はどこに行ってしまったのだろうか？
ここで、Edit Matrix Valueというボタンに注目してみよう。

デザイナーはMatrixアレルギーの人が多い（偏見）
デフォルトだと、下記画像の状態である。

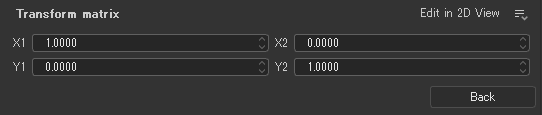
一度、Backに戻ってWidthを80%にしてみよう。

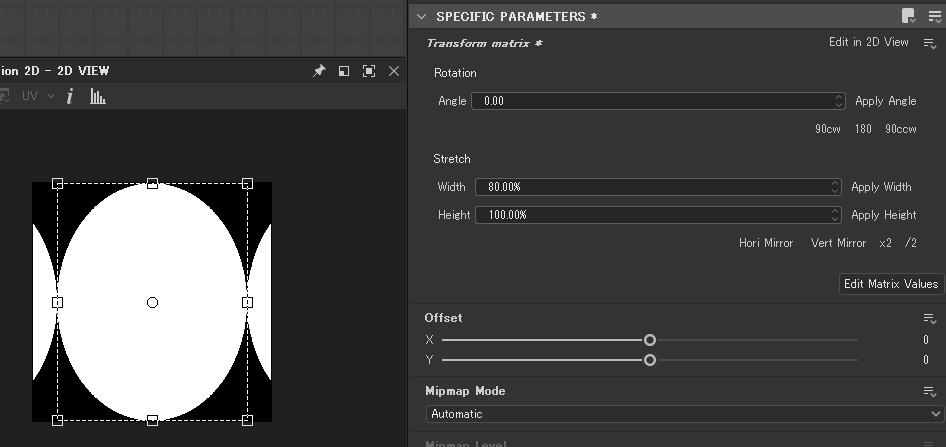
widthを80%で1回Applyした
そして、Edit Matrix Valueボタンを押してTransform Matrixを確認すると…x1が1.0から1.25になっている。

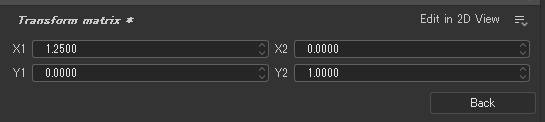
x1が1.0から1.25になった
もういちどwidthに80%適応すると、x1が1.5625の変わっていることが確認できる。

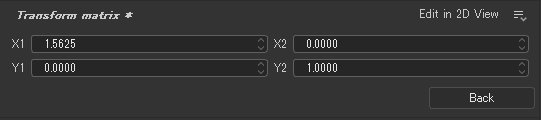
x1が1.25から1.5625になった

Transdorm2DのAngleとScaleが不可逆な理由

どうやら、Transform2Dノードでは入力した値を入力してApplyを押すと、なんらかの計算が行われてtransform matrixの値に変換されるようだ。
そして、その途中式が残らないために後から角度や拡縮を（入力を1とした倍数・角度として）変更することができないのである。

Matrix Valueの正体

なぜ不可逆な計算になっているのかふんわり理解できたとして、どうやってほかのノードのScaleやRotateのような感覚でTransform2Dを使用すればいいのか？
これを理解するためには、ちょっと難しい数字をいじらなければいけない。

結論

結論だけ先に述べておくと、「なんらかの計算」は2次元座標変換^[1]でありその解がパラメータに入力されている。

上記で試したものは、

$$\begin{pmatrix} x'\\ y' \end{pmatrix} = \begin{pmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}$$

であり、この$(x',y')$がパラメータに入力されている。
気持ちとしては、入れたい値は$(s_x,s_y)$なのだけども…

なぜこんな面倒くさいことを…？

わからん、なんでだろう。値はもっててほしい。”””プロシージャル”””なので…

簡単に作れるTransform2Dをつくってみた

transform2Dの中では2次元座標変換の計算がなされていることがわかったら、あとは簡単だ。Transform2DノードのTransform Matrixに、空っぽのFunction Graphを作成してそこで計算させるだけである。

Matrix Valueの出力

ピクセルの位置の列ベクトルは以下のようになっている。

$$\begin{pmatrix} x_1 & x_2 & t_x \\ y_1 & y_2 & t_y \\ 0 & 0 & 1 \\ \end{pmatrix}$$

Matrix Valueの列ベクトルの出力は、float4型の&(x_1,y_1,x_2,y_2)&で設定される。

平行移動

計算は下記である。

$$\begin{pmatrix} x'\\ y' \end{pmatrix} = \begin{pmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}$$

このとき、$(t_x,t_y)$の値はfloat2ノードで出力される、offsrtパラメータの値を読むので、Matrix Valueとは別のFunction Graphで計算される。

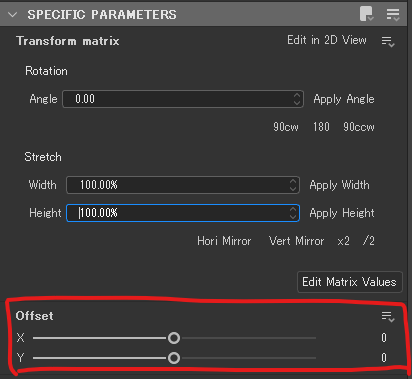
offsetの値が平行移動の値である

拡大縮小

計算は下記である。

$$\begin{pmatrix} x'\\ y' \end{pmatrix} = \begin{pmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}$$

ノードの構造はこんなかんじ。

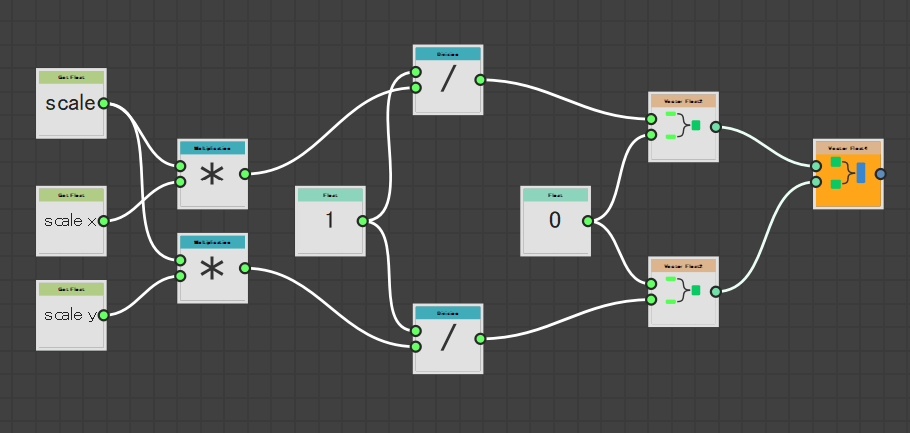
拡大・縮小の関数ノード群

scale、slcale_x、scale_yの３つのパラメータをもつことで柔軟にスケールをかけられる。

回転

計算は下記である。

$$\begin{pmatrix} x'\\ y' \end{pmatrix} = \begin{pmatrix} cosθ & -sinθ & 0 \\ sinθ & cosθ & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}$$

ノードの構造はこんなかんじ。

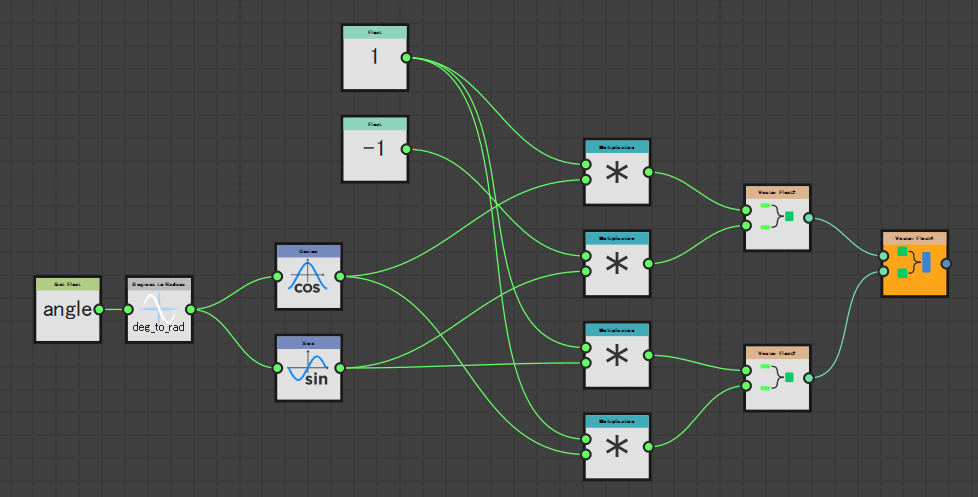
回転のノード群

回転と拡大縮小を分ける理由

上記の「平行移動」「回転」「拡大縮小」は二次元座標空間における幾何学的変換の基本的な変換である。複雑な変形はこの３つの変換が複数組み合わされて実現されている。
このように、いくつかの変換を複数行うことを合成変換と呼ぶ。
この合成変換では、変換の順序を入れ替えると一般には同じ変換にならない。

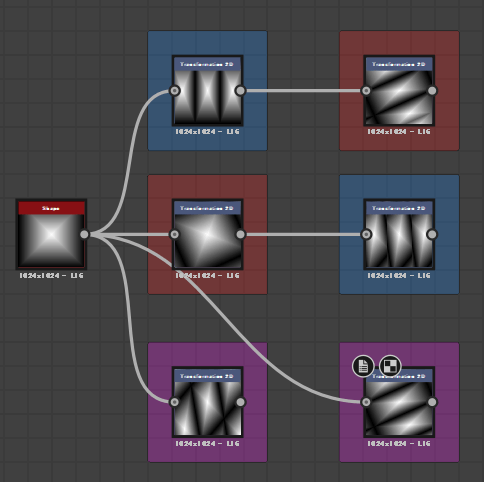
様々な合成変換の例

画像は上から右下にかけて

• スケール単体、回転単体で合成
• 回転単体、スケール単体で合成
• 関数内でMatrix Multiplyノードによる回転*スケールの合成
• 関数内でMatrix Multiplyノードによるスケール*回転の合成
  画像のように、変換の順番によって結果が変わってしまう他、タイリングの設定によっても結果が変わります。

シンプルなノードができた！

このように、シンプルなノードをつくることによってシンプルなinput parmで画像を編集することが可能になります。
簡単なことをしたいだけなのに、なぜこんな苦労をしなくてはいけないのか…
そのうちPixcel Proceccerでノードをつくろうと思います。

脚注

1. 2次元座標変換についての説明はとても長いので割愛します。CG-ARTSのコンピュータグラフィックスエキスパート対応書籍などが参考になります。