Zenn
🎸

音楽をメルスペクトログラム+UMAP + G-meansでクラスタリングしてみた

2024/01/23に公開
Python
scikit-learn
#
librosa
#
umap
#
pyclustering
tech

TL;DR

  • 音楽をメルスペクトログラムで画像化
  • メルスペクトログラムをUMAPで次元削減 + G-meansによるクラスタリングし、似ている音楽ごとを教師なしでグループ分け

動機

今回の検討の発端は、趣味でやっているDTMの悩み事です。DTMとはDesktop Top Musicの略で、パソコンを使った音楽制作のことです。正直下手の横好きなのですが、オリジナルの曲を自作できるのは魅力的です。

さて、DTMをやっていると「サンプルパック」というものをよく使います。サンプルパックとは、オーディオファイル(.wav等)がたくさん入っているパッケージのようなものです。例えば、以下のようなサイトで購入することができます。

このサンプルパックですが、たくさん買ったりダウンロードしたりしていると、DTM用のフォルダが汚れてきて「使いたい素材どこに置いたっけ？」となることが結構あります。欲しいファイルがパッと見つからないと、せっかく思いついたアイデアをすぐに試せなかったり、探すのに時間をとられて消耗したりするので制作のモチベがダダ下がりします。

そこで、クラスタリングなどの技術を使って、似たオーディオファイルを自動でまとめてくれるようなプログラムを作ったらおもしろそうだなと思い、今回の検討に思い至りました。もうすでに誰かが試してそうなアイデアではありますがクラスタリングの練習もかねてやってみたいと思います。

データ

今回はGTZANという音楽分類用のデータセットを使います。このデータセットには音楽(サンプリングレート22.1 kHz, 長さ30秒)が10ジャンルx100曲 = 合計1000曲収録されています。今回はこちらをDTM用のオーディオファイルに見立ててクラスタリングしていきます。
公式サイトからwavを直接ダウンロードすることもできるのですが、今回はhugging faceのデータセットから読み込む方法をとりました。

import datasets

# gtzanのデータセットを読み込み
gtzan = datasets.load_dataset("marsyas/gtzan")
display(gtzan)

# audioファイルから各種データを読み込む．計算速度の問題で最初の5秒間を取り出す。またbit数も8bitに下げる
waveforms = [(gtzan["train"][i]["audio"]["array"][:110250]).astype(np.float16) for i in range(len(gtzan["train"]))]
filepaths = [gtzan["train"][i]["audio"]["path"] for i in range(len(gtzan["train"]))]
labels    = [gtzan["train"][i]["genre"] for i in range(len(gtzan["train"]))]

メルスペクトログラム化

まず、音楽をメルスペクトログラム(MelSpectrogram)に変換します。スペクトログラムとは、横軸を時間軸 [s]、縦軸を周波数の尺度、画素値をパワー[dB]として音をヒートマップ化したもので、とくに周波数軸の尺度をメル尺度(人間の聴覚に基づいた周波数尺度)に変換したものはメルスペクトログラムと呼ばれます。メルスペクトログラム化することで、「音の類似度」を「画像の類似度」として評価できるようになります。コードは以下の通りです。メルスペクトログラムの作成にはlibrosaを利用しています。torchaudioを使えばGPUで計算が行えますが、今回はCPUだけで十分処理できたので使いませんでした。大量のオーディオをメルスペクトログラムにする、メルスペクトログラムをpytorchなどで処理する場合はtorchaudioをつかってみてもいいかもしれません。

# 音源の配列のサイズ。
HOP_LENGTH = 1024
WIN_LENGTH = 1024
N_FFT = 2048
N_MELS = 128
SAMPLE_RATE = 22050

# メルスペクトログラムに変換
img_list = []
for waveform in tqdm(waveforms, desc = "loading audio data..."):
  spec = librosa.feature.melspectrogram(
    y = waveform, sr = SAMPLE_RATE, n_fft = N_FFT, n_mels = N_MELS,
    win_length = WIN_LENGTH, hop_length = HOP_LENGTH, window = hann
  )
  spec = librosa.power_to_db(spec, ref=np.max)

  # リストにappend
  img_list.append(spec)

# 一次元に変換
img_list = [img.flatten() for img in img_list]

ためしに複数のジャンルでスペクトログラムを可視化しました。見た目だけでも各ジャンルごとに特徴がありますね。


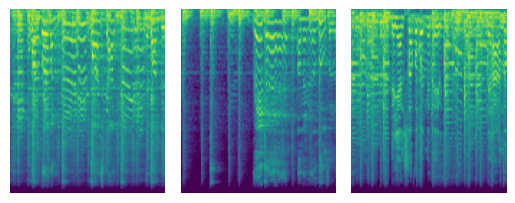
blues


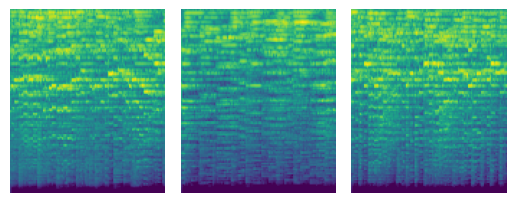
classical


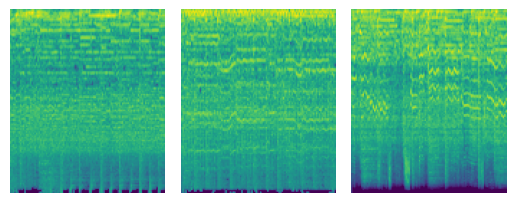
metal

UMAPによる次元削減

次に、UMAPによる次元削減を行います。そのまま特徴量ベクトルをクラスタリングすることも可能ですが、高次元のデータに対して直接クラスタリングをおこなうと球面集中現象などの問題がおきます。そのため、次元削減を行って低次元のデータに変換してからクラスタリングを行うのが一般的だと思います。
今回は次元削減手法の中でも比較的新しい手法であるUMAPを使います。次元削減手法だとt-SNEも有名ですが、UMAPはt-SNEよりも高速・高性能に次元削減が行えます。原理の説明は以下サイトがわかりやすかったです。

https://qiita.com/odanny/items/06ab88353bcee7bf6aa7

ライブラリのインストールとUMAPによる次元削減のコードは以下の通り。umap-learnを使うとscikit-learnのPipelineに対応した形で適用できるので、せっかくなら適用しておきましょう。
また、データ間の距離尺度としては

  • ユークリッド距離
    • 画像を一次元配列に展開したもののユークリッド距離をとる
  • Dice係数
    • 集合AとBの全要素数に対する共通部分の割合
    • 画像の類似度やセグメンテーションの性能を測るのにつかわれる

の2通りを試してみます。

!pip install  umap-learn

import umap

# UMAPでの次元圧縮のパイプライン
pipeline2d = Pipeline([
              ("Standarization", StandardScaler()),
              ("UMAP", umap.UMAP(
                n_components = 2, n_epochs = 500,
                # metric = "euclidean",
                metric = "dice",
                verbose = 2, random_state = 42
              ))
])

# UMAPによる次元圧縮で2次元に圧縮
embedding2d = pipeline2d.fit_transform(img_list)

# 結果をpandas DataFrameに変換
df_res2d = pd.DataFrame(
              {
                  "x": embedding2d[:, 0], "y": embedding2d[:, 1],
                  "genre": labels,
                  "genre_label" : [os.path.basename(f).split(".")[0] for f in filepaths],
                  "file_path": filepaths
              })

px.scatter(
    df_res2d, x = "x", y = "y", color = "genre_label",
    hover_data = ["genre_label"], labels = "genre_label", symbol = "genre_label"
)

UMAPによる次元削減結果は以下の通りです。データセットでの各音楽ジャンルのラベルを点の色で表現しています(紛らわしいですが、クラスタリングはまだ行ってません。データセットに元々ついていたジャンルのラベルを色で表現しています)。

ユークリッド距離の場合、各点がジャンルに関係なくあべこべに配置されており、次元圧縮が上手くいっていないことがわかります。

Euclidean

Dice係数を使った場合には、同じジャンルの点が比較的近くに配置されました。複数のジャンルが混ざり合ってしまっている部分も散見されますが、全体的にはよい次元圧縮ができています。

Dice

今回のデータにおいてはDice係数を使った次元圧縮が最も有望そうです。そのため、以降はDice係数を距離指標にして次元圧縮を行った結果をクラスタリングに使います。

G-meansによるクラスタリング

UMAPで次元削減したデータをクラスタリングします。今回はクラスタ数を自動決定できるG-meansを採用しました。実装にはpyclusteringを使用しています。
最大のクラスタ数は30としました。

!pip install pyclustering

from pyclustering.cluster.gmeans import gmeans
from pyclustering.cluster.xmeans import xmeans
from pyclustering.cluster.center_initializer import kmeans_plusplus_initializer

# G-means実行
X = (df_res2d[["x", "y"]]).to_numpy()
gm_c = kmeans_plusplus_initializer(X, 2).initialize()
# gm_i = gmeans(data=X, initial_centers=gm_c, kmax=30, ccore=True)
gm_i.process()

# クラスタリングの結果をDataFrameに保存
z_gm = np.ones(len(df_res2d["x"]))
for k in range(len(gm_i._gmeans__clusters)):
    z_gm[gm_i._gmeans__clusters[k]] = k+1
df_res2d["cluster"] = z_gm
df_res2d["cluster_label"] = ["Cluster_{:d}".format(int(c)) for c in z_gm]

# プロット
fig = px.scatter(
    df_res2d, x = "x", y = "y", color = "cluster_label",
    hover_data = ["cluster_label"], labels = "cluster_label", symbol = "cluster_label"
)
fig

クラスタリングを行った結果は以下の通りです。今回は16個のクラスタに分かれました。10個のジャンルに分かれているデータセットを16個のクラスタに分けてしまっているので、すこし細かく分割しすぎています。

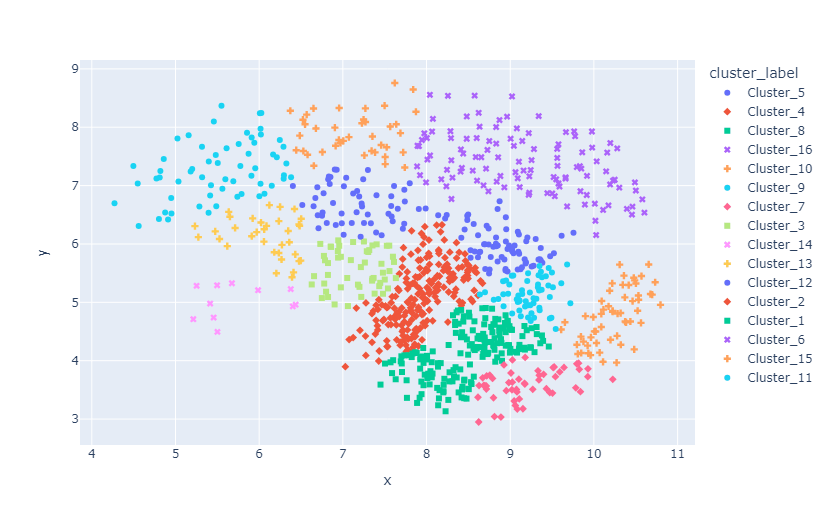
各クラスタ内のジャンルの内訳を棒グラフにしたものは以下の通りです。UMAPによる次元削減で各ジャンルが近くに配置されたおかげで、大半のクラスタにおいて1個もしくは2個のジャンルの割合が突出していることがわかります。各クラスタの音楽ジャンルは1~2種類に統一されており、有意なクラスタリングができたといえます。

クラスタリングの結果に基づいてフォルダ分け

最後に、クラスタリングの結果に基づいてオーディオファイルをフォルダ分け・zipに圧縮します。コードは以下の通りです。

import zipfile
with zipfile.ZipFile("path/to/zip", "w", 
                     compression=zipfile.ZIP_DEFLATED, compresslevel=9) as zf:
  for c in np.unique(df_res2d["cluster"]):
      # クラスターがcに属するファイルパスをリストアップ
      file_list = df_res2d[df_res2d["cluster"] == c]["file_path"]

      # サブフォルダを作って圧縮
      for f in tqdm(file_list):
        zf.write(f, arcname = "cluster_{0:d}/{1:}".format(int(c), os.path.basename(f)))

まとめ

メルスペクトログラム化 + UMAP + G-meansを使うことで、音楽のデータセットをある程度有意なクラスタに分割することができました。実際のDTMで使う音源でも同様の性能が出るかは未知数ですが、軽い気持ちで試した割には有望な音楽クラスタリング手法だと思います。
またメルスペクトログラム・UMAP・G-meansのいずれも比較的軽い処理(少なくともCPUのみで完結し、数分 ~ 数十分待たされる処理ではない)点もこの手法のいい点だと思います。

Discussion