CTFに一年ぶりに参加したWaniCTF2024 Writeup
前置き
SECCON CTF 2023 でCryptoの一番簡単なやつを解いたっきりCTFに触れていなかったのですがパソコン全般をちょっと勉強して自信がついてきたのでCTF復帰したいなーと思っていて、ちょうど知り合いが作問しているらしいのでWaniCTFに出ることにしました。一年ぶり二回目の挑戦です。
結果
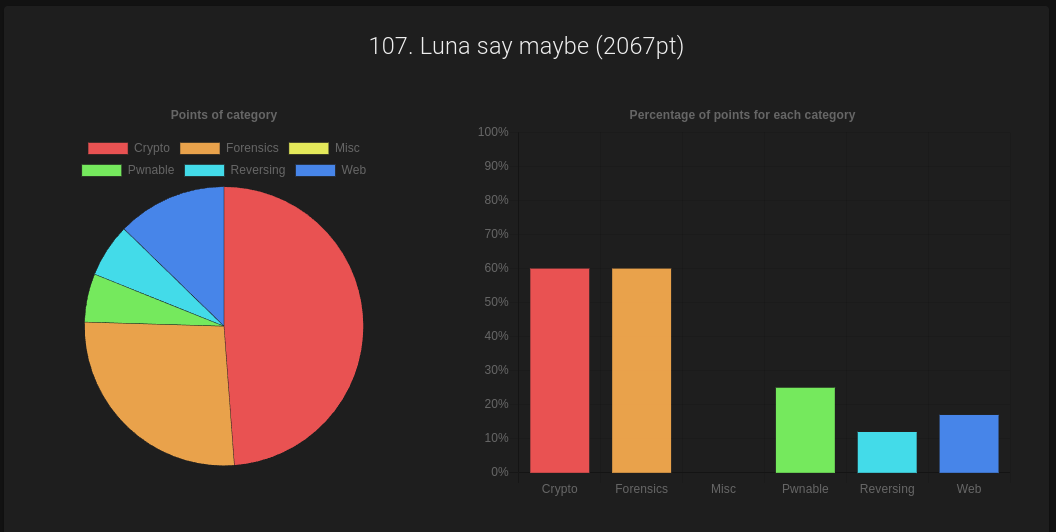
一人で参加して107位でした。CTFのための対策は一切していなかった割には頑張ったほうだと思います。
Crypto
暗号は特に本を読んで勉強していたので自信がありました。
結果もかなり良かったと思います。
beginners_rsa
コードを読みます。すると
適当にググるとmsieveというなんかこうすごく速くてめっちゃいいかんじの素因数分解の実装が見つかるので投げると素因数分解ができて
beginners_aes
鍵とIV(初期化ベクタ)をよく見る (よく見なくても一番上にある) と 1 byte ずつしかパターンがないことがわかります。
合計で
replacement
chall.pyを読むと平文を一文字ずつハッシュを取ってリストにしていることがわかります。
日記の文字が全てASCII文字だと仮定してハッシュ値を全探索して同じハッシュ値であればその文字を割り当てます。
一応コード
import hashlib
enc = eval(open("my_diary_11_8_Wednesday.txt").read())
ans = ""
for i in enc:
for j in range(128):
if int(hashlib.md5(str(j).encode()).hexdigest(), 16) == i:
ans += chr(j)
break
print(ans)
Easy calc
これは明らかにどのようにf(s,p)を逆算するかという問題です。
にらめっこしたりwolframに投げると
import os
import random
from hashlib import md5
from Crypto.Cipher import AES
from Crypto.Util.number import long_to_bytes, getPrime
p = 108159532265181242371960862176089900437183046655107822712736597793129430067645352619047923366465213553080964155205008757015024406041606723580700542617009651237415277095236385696694741342539811786180063943404300498027896890240121098409649537982185247548732754713793214557909539077228488668731016501718242238229
A = 60804426023059829529243916100868813693528686280274100232668009387292986893221484159514697867975996653561494260686110180269479231384753818873838897508257692444056934156009244570713404772622837916262561177765724587140931364577707149626116683828625211736898598854127868638686640564102372517526588283709560663960
ciphertext = "9fb749ef7467a5aff04ec5c751e7dceca4f3386987f252a2fc14a8970ff097a81fcb1a8fbe173465eecb74fb1a843383"
def inv_f(A, p):
return A * pow(A + 1, -1, p) % p
def decrypt(c: bytes, key: int) -> bytes:
key = long_to_bytes(key)
key = md5(key).digest()
cipher = AES.new(key, AES.MODE_CBC)
return cipher.decrypt(c)
s = inv_f(A, p)
print(decrypt(bytearray.fromhex(ciphertext), s))
dance
これはコードが長いので読むのが少し大変ですががんばります。
頑張って読むとmycipher.pyのMyCipherクラスのencrypt関数で暗号化の処理をしていることがわかるのでそこを読みます。
一見複雑そうな処理に見えますが、今回は暗号文が 64 byte 以下なのでfor文が実行されず、実質的には一度だけxorをする処理になっていることがわかります。
xorの逆演算はxorなのでencrypt関数で復号も同時にでき実装の手間が省けます。
鍵はchall.pyのRegister関数で作られているのがわかりますが、鍵には分×秒×random.randintで randint(0,10)に
from utils import *
import hashlib
import datetime
import random
from mycipher import MyCipher
d = {}
isLogged = True
current_user = "gureisya"
ciphertext = "061ff06da6fbf8efcd2ca0c1d3b236aede3f5d4b6e8ea24179"
def make_token(data1: str, data2: str):
sha256 = hashlib.sha256()
sha256.update(data1.encode())
right = sha256.hexdigest()[:20]
sha256.update(data2.encode())
left = sha256.hexdigest()[:12]
token = left + right
return token
for minute in range(60):
print(f"{minute=}")
for second in range(60):
for check in range(11):
data1 = f"user: {current_user}, {minute}:{second}"
data2 = f"{current_user}" + str(check)
token = make_token(data1, data2)
sha256 = hashlib.sha256()
sha256.update(token.encode())
key = sha256.hexdigest()[:32]
nonce = token[:12]
cipher = MyCipher(key.encode(), nonce.encode())
plaintext = cipher.encrypt(bytearray.fromhex(ciphertext))
if b"FLAG" in plaintext:
print(plaintext)
speedy
これは本当にhardですか?
コードをよく見ると鍵のX,YのうちXの方は平文にブロックごとに埋め込まれていることがわかります。
X_{i+1}=(rotl(X_i, 24) ^ X_i ^ (X_i << 16) ^ Y_i ^ (Y_i << 16)) & ((1 << 64) - 1)なので、XORを取ってあげると Y_i^(Y_i << 16) がわかり、下の桁から順番に計算すれば Y も求めることができます。
X と Y がわかったら後は key を計算して逆向きに処理するだけで終わりです
from cipher import MyCipher
from Crypto.Util.number import *
from Crypto.Util.Padding import *
import os
ct = b'"G:F\xfe\x8f\xb0<O\xc0\x91\xc8\xa6\x96\xc5\xf7N\xc7n\xaf8\x1c,\xcb\xebY<z\xd7\xd8\xc0-\x08\x8d\xe9\x9e\xd8\xa51\xa8\xfbp\x8f\xd4\x13\xf5m\x8f\x02\xa3\xa9\x9e\xb7\xbb\xaf\xbd\xb9\xdf&Y3\xf3\x80\xb8'
def rotl(x, y):
x &= 0xFFFFFFFFFFFFFFFF
return ((x << y) | (x >> (64 - y))) & 0xFFFFFFFFFFFFFFFF
X_lis = []
for i in range(0, 64, 16):
X_lis.append(bytes_to_long(ct[i : i + 8]))
rem = (X_lis[1] ^ rotl(X_lis[0], 24) ^ X_lis[0] ^ (X_lis[0] << 16)) & ((1 << 64) - 1)
y0 = rem & ((1 << 16) - 1)
for i in range(16, 64):
y0 |= (1 << i) * (((rem >> i) & 1) ^ ((y0 >> (i - 16)) & 1))
Y_lis = [y0]
key_lis = []
MOD = (1 << 64) - 1
for i in range(4):
X = X_lis[i]
Y = Y_lis[i]
sum = (X + Y) & MOD
Y ^= X
key = []
for _ in range(8):
key.append(sum & 0xFF)
sum >>= 8
key_lis.append(key[:])
Y = rotl(Y, 37) & MOD
Y_lis.append(Y)
pt = b""
cntr = 1
for tmpi in range(0, len(ct), 16):
i = len(ct) - tmpi - 8
block = ct[i : i + 8]
pt = bytes([block[j] ^ key_lis[-cntr][j] for j in range(len(block))]) + pt
cntr += 1
print(pt)
Forensics
これは一ミリも勉強してこなかったのですがなぜか 4 問も解けて喜んでいます
tiny_usb
マウントすると中に画像が入っているので見るとflagが書いてあります
Surveillance_of_sus
バイナリの先頭に RDP8bmp と書いてあるのでそれでグーグル検索します。
一番上にこの問題でやってほしいこと (キャッシュファイルから画像を復元すること) ができるツール があるのでこれを使うと画像が見えます。
codebreaker
想定解かどうかはおいておいて https://pixilart.com で気合でわかるところをを復元するとこうなって普通にQRコードリーダーで読み込むことができます。

I_wanna_be_a_streamer
wiresharkで見るとRTP形式のデータが送信されていることがわかります。ヒントによるとH.264形式のエンコードらしいです。
色々調べるとvideosnarfというツールでパケットキャプチャからH.264を解析して復元することができることがわかったのでやります。
そのままの264だと見られなかったのでffmpegでmp4に変換したらvlcで見られました。
Misc
一問も解けませんでした🥲🥲🥲
Pwnable
do_not_rewrite、解けそうだったのですがうまくcanaryを騙せず...
nc
チュートリアルです。
やります。
Reversing
home、constructFlag関数の難読化がすごくて頑張ったのですが無理でした...
lambda
こういうことはChatGPTに任せるのが一番楽です。
Web
Bad_Worker
Fetch FLAG.txt を押してネットワークを見ると https://web-bad-worker-lz56g6.wanictf.org/FLAG.txt にアクセスしていることがわかります。
curl してみるとなんかFLAGが返ってきました。
仕組み理解してなくてごめんなさい...
pow
同じ値をを何度も一つのリストに入れてもOKなのでめちゃくちゃでかいリストを作ってリクエストを送ると通ります。
さいごに
CTFの楽しさに気づいたので今後も継続的に参加したいと思いました。
Web, Reversingに関してはもっと勉強しようと思います。

Discussion