🐍
単回帰ってなんやねん

2025/03/19に公開
 はじめにどもども、フリーランスエンジニアとして働いている井上弥風（いのうえみふう）です。
最近魚の飼育に凝ってまして、最初はネオンテトラを15匹だけ購入したつもりが、なぜか今55匹になってる今日この頃です。
もうハマりにハマっちゃって水槽の水でミニトマト育て始めちゃってる（クソ情報失礼しました）


 著者プロフィール私は元々バックエンド・インフラメインで仕事をしていて、AI周りの学習は2025年の2月に始めました。
とりあえずG検定・AWS AIF周りの試験勉強をして、何となく全体像を知った後、実際にXGBoostという決定木ベースのモデルで開発を始めました。
今もこのモデルで開発をしていて、あわよくば収益化を目指している（マジで可能性あると思っている領域なのでおもろい）のですが、やっぱり我流で進めているので色々と壁にぶつかってる、、、って状況です。

 この記事を書いた背景モデルを利用した開発でぶつかった内容を言語化することで知識をより定着させたいと思い、今回ぶつかったのが「単回帰」だったので、そのまま記事にしました。

 この記事で記載すること・しないこと記載する内容
単回帰に関する基礎概念
一次関数についての解説
Pythonで単回帰を動かす例

記載しない内容
AIに関する基礎的な知識
統計学に関する基礎的な知識


 対象読者線形回帰・単回帰について基礎的な理解をしたい方

 線形回帰とは？まずは、単回帰の基本となる「線形回帰」について理解していきます。
線形回帰は、従属変数（目的変数）と1つまたは複数の独立変数（説明変数）の間に線形な関係があると仮定し、その関係性を数式（線形モデル）で表現する手法です。

一般的には最小二乗法などを用いて、観測データに最もよく当てはまる直線や平面を求め、将来の予測や因果関係の解析に活用します。
この文章を読んでもいまいち分かりませんが、簡単に言うと線形回帰はデータを直線で表す手法です。
例えば、勉強時間とテストの点数って基本的には比例しますね。
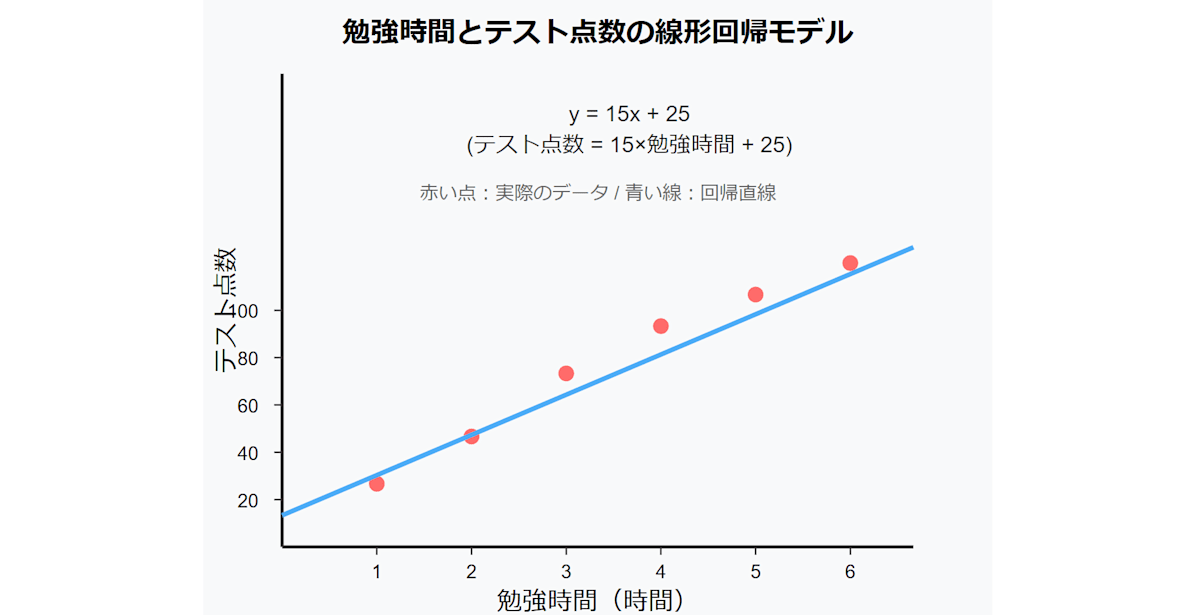
つまり、勉強時間とテストの点数には何らかの関係性があるわけですね。その「何らかの関係性を見つけて、いい感じに線を引く手法」が線形回帰です
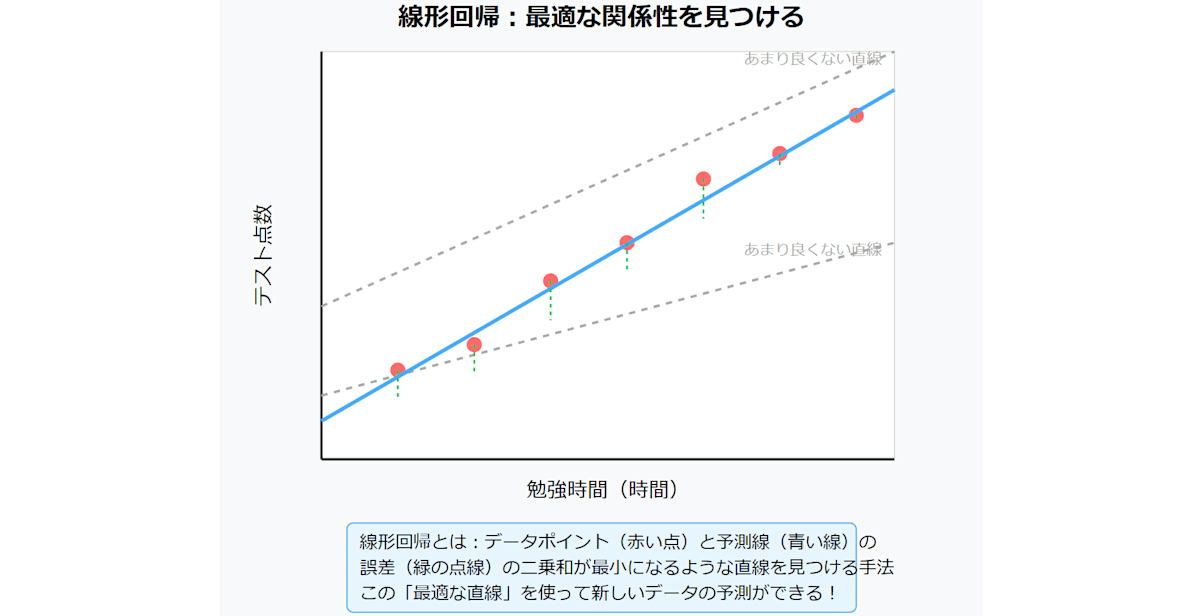
なぜ「何らかの関係性」を見つけないといけないのでしょうか？というか見つけるとどういったメリットがあるのでしょうか？

簡単に言えば、何らかの関係性が分れば、「テストの点数」が分からなくても「勉強時間」からテストの点数を予測することができますね。

実社会では勉強時間からテストの点数が予測できてもあまり役には立たないですが、線形回帰を利用すれば役立つこともあるわけですね
その線形回帰の基礎の基礎が「単回帰」だったりするわけです（後述します）

 線形回帰を学ぶ前に、説明変数と目的変数について線形回帰を学ぶ前に、まず「説明変数」と「目的変数」という概念を理解しましょう。

簡単に言えば、説明変数は「原因」、目的変数は「結果」です。
詳しく見ていきましょー

 具体例①：ビールの販売と気温たとえば、あなたがサッカースタジアムでビールの販売を担当しているとします。
あなたは「ビールは気温が高いと多く売れる」ことに気付きました。

実際の販売記録が以下です。
上記の図での説明変数・目的変数以下です。
横軸：最高気温（原因となる要因＝説明変数）
縦軸：販売数（気温の影響を受ける結果＝目的変数）
つまり、この図から、「ビールの販売数は気温によって変動する」という関係が見て取れるわけですね。

（意外と単純ですよね）
!もう少し例を出してみる
具体例②：雨とダムの水の蓄積

もう少し例を出すと、例えば雨が降った結果、ダムに水がたまる場合を考えてみます。
この場合は以下の説明変数と目的変数に分けられますね。
説明変数：雨の降水量（原因）
目的変数：ダムの水の蓄積量（結果）
具体例③：車の走行距離とガソリン量

さらに、車にガソリンを入れた結果、走行距離が延びる場合を考えてみます。
説明変数：投入したガソリンの量（原因）
目的変数：車が走った距離（結果）
整理すると
説明変数＝原因となる要因
目的変数＝原因の結果として現れる現象
ですね！

 単回帰単回帰は、一つの説明変数（原因）から目的変数（結果）を予測するための手法です。

線形回帰の中でも、「説明変数が一つの場合」を指し、シンプルなモデルで予測や関係性の解釈が可能な点が特徴です。
例えば、先ほどと同じでくあなたがビールの販売員をしているとします。

ビールの販売数は気温によって変動するとします。


日付
気温(°C)
販売数(本)


8月1日
32
201

8月2日
29
185

8月3日
34
198

8月4日
31
180

8月5日
35
209

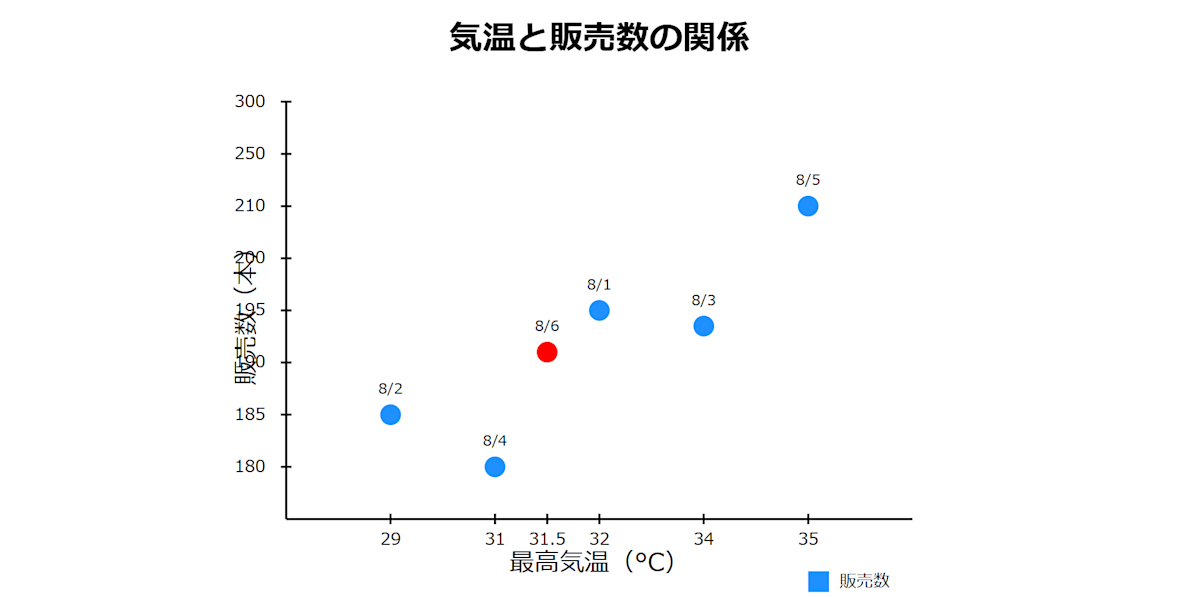
下記がその散布図です。
では、次の日（8月6日）の気温が31.5度だと仮定して、上記の散布図を参考に、販売数を予測してみます。

予測する販売数は大体以下のようになるのではないでしょうか？
ここでポイントなのが、8月6日のビールの販売数を予測する際に参考にしたデーータが「気温」というデータの一つだけ、という点です
改めて単回帰を説明すると、単回帰とは「一つの説明変数から目的変数を予測する」手法です。

つまり意外と簡単なもので、単に一つのデータを基に予測をする、というのが単回帰な訳です。

 重回帰続いて重回帰について説明します。

結論から言うと、重回帰は、複数の説明変数（原因）から目的変数（結果）を予測する手法です。
単回帰では「説明変数が一つ」だったのに対し、重回帰では「複数の要因を同時に考慮できる」ため、より複雑な現実の状況をモデル化することが可能です。
不動産会社が住宅価格を予測する場合を考えてみましょう。

単回帰だと、たとえば以下のような単一の要因でしか予測が出来ませんね。
部屋数から住宅価格を予測する
家の面積から住宅価格を予測する
築年数から住宅価格を予測する
...
しかし、実際の住宅価格は部屋数、面積、築年数、立地、周辺環境など、複数の要因の組み合わせで決まります。

このような場合、各要因を説明変数として同時にモデルに組み込むのが重回帰な訳です。

 まとめ単回帰：説明変数が1つの場合の予測手法
重回帰：複数の説明変数を用いて予測する手法
概念としては、「説明変数の数が1つか2つ以上か」という違いですが、実際には利用する数式や解析方法は大きく異なります。

重回帰では、各説明変数が目的変数に与える影響を同時に考慮できるため、より現実に即した予測が可能になるわけですね。
ではでは、ここからは単回帰をメインにフォーカスし、具体的に「どのように説明変数から目的変数を予測するのか？」という疑問を紐解くため、基本的な数式を見ていきます。

数式と言っても内容は中学生レベル、かつ数学嫌いの私が理解出来た内容なので、あまり気構えずに見ていきましょう^^

 単回帰を理解する前に、一次関数を理解する皆さんは一次関数をご存じでしょうか？

私は完全に忘れていました^^
ので、ここからは一次関数を知らない人、または習った気がするけど忘れている人向けに一次関数を説明します。

ある程度理解がある方は流し読みしていただければ大丈夫です。

 温度が上がるとビールが売れる例で考えるでは、先ほどと同じように「気温が上がるとビールが売れる」という状況を基に一次関数の概念を説明していきます。
下記がビールの販売数などが記載された過去のデータです。


日付
気温(°C)
販売数(本)


8月1日
32
201

8月2日
29
185

8月3日
34
198

8月4日
31
180

8月5日
35
209

下記がその散布図です。

 人間が温度とビールの販売数を基に次の日の販売数を予測する場合たとえば、次の日（8月6日）のビール販売数を予測する際、気温が31.5度の場合、多くの人は直感的に「こんなあたりかな？」と予測する課と思います。
これは、人間が「勘」や「雰囲気」で予測している例ですね。

意識的に複雑な計算をせず、過去の経験や感覚に頼っているという点が特徴です。

 AIが温度とビールの販売数を基に次の日の販売数を予測する場合一方、AIは人間のような直感を持たないため、数式を用いて次の日の販売数を予測するわけです。

その予測方法が、単回帰の場合は「一次関数」を利用して予測するわけです。
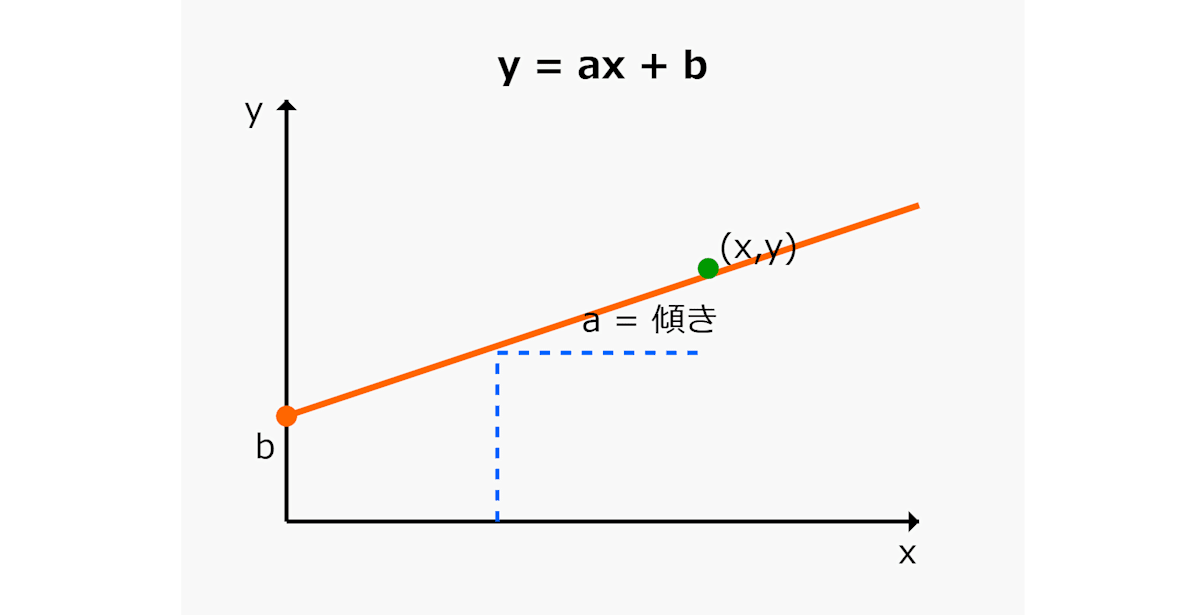
まず、一次関数の基本的な式は以下です。

y=ax+b
ここで、各変数は以下のようになります。
x：説明変数（今回の例では気温）
y：予測したい目的変数（今回の例では販売数）
a：気温が1度上がるごとに販売数がどれだけ変わるかを示す係数（傾き）
b：気温が0度のときの基準値（切片）
一次関数の特徴は、xの変化に対してyの変化が一定であるため、グラフにすると直線になる点です。
!直線になる？

「直線になる」というのをより噛み砕いて言うと、xが1増えるたびにyも同じ量増える、つまり変化の割合が一定という事ですね
変化の割合が一定なので、xが例えば段階的に増えても、yも同じ量増えていくので、グラフにすると直線になる訳ですね

 ビール販売数の予測例実際に、ビール販売数を予測するための一次関数の式は以下のように表せます。

販売数=a×気温+b
yは予測したい目的変数であり、今回予測したいのが販売数のため、一番左のyが目的変数ですね
次に、xは入力、今回の例で言うと販売数を予測するための説明変数となるため、気温 = xです。
ではここでaを10、bを-15にしてみましょう（数値は適当）
この場合、気温31.5の場合の販売数を予測したい場合、以下の数式になります

10×31.5-15=300
少し上過ぎますね。

ではaを7、bを30にして再度計算してみましょう

7×31.5-30=190.5
何となく、それっぽくなってきましたね。

 整理するとここまでの内容を整理すると、単回帰という手法は、一次関数で表現できるシンプルな予測モデルな訳です。

つまり、機械学習の線形回帰における単回帰アルゴリズムは、一見複雑に見えても、その実態は基本的な一次関数（y = ax + b）なんですね。
ここまでの例は、係数aと切片bを適当な値に設定して予測していましたが、実際にはいくつかの手法により、aとbの最適値を求めることができるんですね（後述）。
!「モデル学習が指すもの」

一般的に、モデルは学習（＝パラメーターの最適化）を繰り返すことで性能が向上します。

人間でいえば「記憶する」ことが学習と捉えられるかもしれませんが、AIの場合は、正しい予測を行うために必要なパラメーター（aやb）の最適な値を見つけ出すことが学習そのものです。
先ほどの例で、aとbを適切に調整することで、気温から翌日のビール販売数が予測できるようになったのは、まさにこのパラメーター最適化の成果な訳ですね。

モデルの内部は数式で構成されており、正確な予測に必要なのは、「記憶」ではなく「最適なパラメーターを見つけるプロセス」な訳です。
「学習」と言うとどうしても「何かを学んでいる・記憶している」ようにとらえられますが、AIモデルにおける学習は基本的に「パラメーターの最適化」な訳ですね^^

 パラメーター最適化の基礎概念まず、先ほどの内容を振り返ると、aとbを適切な値に置き換えることで、正しい販売数を予測することが出来ました。

販売数=a×気温+b
つまり、「aとbを最適化すること」が正しい予測をするための鍵な訳ですね。
!パラメーター
パラメーターとは、「モデルの性能を向上させるために最適化する数値」のことです。

単回帰においては、a（傾き）とb（切片）がこれに該当します。
パラメーターの最適化と言っても、そのプロセスは単純ではなく、残差や最小二乗法、正規方程式などの概念が登場するため、ここではまずそれらの基礎となる「残差」について説明します。

 残差結論として、残差はとは「実測値と予測値の差を示す指標」です。

残差が小さいほど、モデルの予測は実測値に近いということになります。
具体的に見ていきましょう。
例えば、下記のデータがあるとします。


No.
入力値(x)
切片(b)
傾き(a)
予測値(y)
実測値(正解)


1
1
1
1
2
2

2
2
1
1
3
4

3
3
1
1
4
6

実際にNo1 ~ 3の残差を計算してみます。
残差の求め方は非常にシンプルで、

残差=実測値-予測値
​です
No.1
予測値：2=1×1+1
実測値も2なので、残差はe=2−2=0

No.2
予測値：3=1×2+1
実測値は4なので、残差はe=4−3=1

No.3
予測値：4=1×3+1
実測値は6なので、残差はe=6−4=2

残差は合計3で、残差の最小値は0です。これが何を意味するのかと言うと、「ズレがない」事を意味し、つまりは正確な予測が出来ていることを意味します。
残差が大きい場合、イメージとしては下記のように実際の値と予測値に差があることを意味します。


 モデルの指標評価個々のデータ点での残差は、「どれだけ予測が外れたか」を示します。

しかし、モデル全体の性能を評価するには、全データに対する誤差を一つの指標にまとめる必要があるわけです。

これは、「モデル全体としてどれだけ誤差が大きいか」を把握するためですね。
モデル全体としての誤差を計算する手法は以下のようにいくつかあるのですが、たくさん紹介しても難しいので、ここではSSEとMSEに絞って紹介します。
誤差の算出方法の種類
SSE
MSE
RMSE
決定係数R²

SSE (Sum of Squared Errors) / 平方和

SSEは、予測値と実測値の差（残差）を二乗し、その合計を求めたものです。

つまり、先ほどの例で言うと、各残差を二乗して足し合わせれば、SSEが求まります。
No1の残差：2 - 2 = 0² = 0
No2の残差：4 - 3 = 1² = 1
No3の残差：6 - 4 = 2² = 4
SSE = 0 + 1 + 4 = 5
!何で二乗するの？
残差とは「予測の誤差」ですが、もし誤差の符号（プラス・マイナス）が混ざっていると、単純に足し合わせると互いに相殺されてしまうんですね。

例えば、以下のような距離の予測を考えてみます。
横浜から東京の距離
実測値：100km、予測値：80km → 残差：100 - 80 = 20km

横浜から埼玉の距離
実測値：150km、予測値：200km → 残差：150 - 200 = -50km

横浜から群馬の距離
実測値：200km、予測値：170km → 残差：200 - 170 = 30km

これらを単に足すと、

20+(−50)+30=0
本当は大きな誤差があっても、プラスとマイナスが相殺されてしまい、誤差がゼロになってしまいます。つまり予測にズレがあるのにずれがないことになっちゃうわけですね。
そこで、各残差を二乗することで符号の影響を取り除き、全て正の値にして合計を出すわけですね。

20² + (- 50)² + 30² = 400 + 2500 + 900 = 3800
MSE (Mean Squared Error) / 平均二乗誤差

MSEは、SSE（残差の二乗和）をデータの数で割った平均値です。

例えば、上記の例ではSSEが3800で、データ数が3だったため、

20² +  (- 50)² + 30² = 400 + 2500 + 900 = 3800 / 3 = 1266.6
データの数で割る理由は、例えばモデルAとモデルBの性能比較をしたい際などに、SSEだとデータ数が多ければその分SSEの値も多くなってしまうため、単純比較ができません。

しかし、データの数で割るとデータ数が違くてもモデル間の比較をできるため、場合によってはMSEを利用したりするわけですね。
いずれの指標も「予測がどれだけ実測に近いか」を把握するためのものなので、どれか一つを見ればいいというわけではなく、状況に応じて確認していきます。

 モデルのパラメーターの最適化ここまで、「残差を求める」→「SSEやMSEで誤差を把握する」という流れを説明してきました。次は、この誤差（ズレ）を最小化して、最適なパラメーター a と b を求める方法について説明していきます。
最小二乗法による導出

「予測値と実測値の差をできるだけ小さくしたい」と言っても、具体的にどうパラメーターを動かせばいいかは簡単ではありません。しかし、単回帰の世界では「最小二乗法」と呼ばれる方法を使うことで、明確にaとbを求めることができます。
最小二乗法とは、「SSE（残差の二乗和）が最小となるように a と b を選ぶ」という考え方です。SSEを次のように書くと、
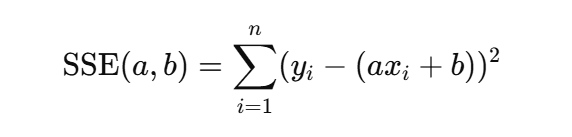
これが最小になるような a と b を見つけたいわけです。
a で微分して 0 と置く
b で微分して 0 と置く
という手続きを踏むと、連立方程式が解けるようになっています。

（具体的な式変形はやや長いですが、微分のルールを使ってゴリゴリ展開すると解が得られます。）
正規方程式で解く

実は、最小二乗法は「正規方程式（normal equation）」と呼ばれる形を使うことで、一気に解くこともできます。単回帰ではまだ式がシンプルなので「微分して解く」方法でも構わないのですが、多変量になったりデータ数が多かったりすると、行列を使う正規方程式の方が計算手順としては整然としています。
単回帰の場合、正規方程式を使わない「公式」がすでに用意されているので、最終的には以下のような形で簡単に出せます。
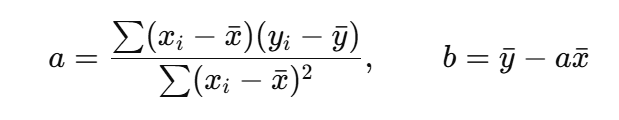
直感的には、「x が増加するときに y もどれだけ増加するか」という関係を見ながら傾きを決めて、あとは平均を使って切片を求めているイメージです。

 まとめパラメーターの最適化は計算の連続で、それを記事でやると冗長になるため今回は詳細を省きましたが、モデルの学習とはいわばパラメーターの最適化です。
そして、回帰モデルに限らずLLMや画像解析などでも、それらアルゴリズムに適したパラメーターの最適化手法、つまり計算式があるわけです。
そう考えると、魔法のように思えるChatGPTやClaude、画像や音声生成系サービスも、数学の上に成り立っているわけで、AIのベースはあくまで数式なんですね。

 単回帰の学習と予測ではここから、実際にPythonを利用して単回帰モデルを動かしていきます。

 利用するデータセットについて今回利用するのは「住宅価格」に関するデータセットです。

具体的には、ボストン近郊の住宅情報と価格に関するデータです。
!ボストンはアメリカのマサチューセッツ州にある場所で、日本で言う市みたいなものですね（よー知らんけど）
※ちなみに、この「住宅価格データセット」はカリフォルニア大学アーバイン校が無償で提供してくれているデータセットです。

 データセットの内容データセットの内容は以下です。


変数名
詳細


CRIM
人口1人あたりの犯罪発生率

ZN
25000平方フィートを超える住居エリアの割合

INDUS
小売以外の商業用地が占める面積の割合

CHAS
チャールズ川沿い地域の有無を示すダミー変数（1: 該当、0: 非該当）

NOX
大気中のNOx濃度

RM
1940年以前に建てられた建物の割合

DIS
主要な5つの雇用施設までの距離

PAD
環状高速道路へのアクセスのしやすさ

TAX
1万ドルあたりの不動産税率の総額

PTRATIO
各町における児童と教師の比率

B
町毎の黒人比率を1000(Bk-0.63)^2で算出

LSTAT
低所得層に従事する住民の割合

MEDV
所有者が占有する住宅の中央値（単位: ＄1000）

また、実際に下記URLでブラウザからでもアクセスできます。

https://archive.ics.uci.edu/ml/machine-learning-databases/housing/housing.data
↓こんな感じ


 学習データの読み込みまずは、学習データとしてボストン住宅価格データセットを読み込みます。以下のコードで、データを取得して前処理を行っています。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error
from sklearn.linear_model import LinearRegression

# データセットの読み込み
df = pd.read_csv(
    "https://archive.ics.uci.edu/ml/machine-learning-databases/housing/housing.data",
    header=None,
    sep="\\s+",
)
df.columns = [
    "犯罪率",       # CRIM: 町ごとの犯罪発生率
    "大規模住宅地率", # ZN: 25,000平方フィート以上の住宅地の割合
    "非小売業率",   # INDUS: 非小売業が占める土地の割合
    "チャールズ川ダミー", # CHAS: チャールズ川沿いなら1、そうでなければ0
    "窒素酸化物濃度",    # NOX: 窒素酸化物濃度（10ppmあたり）
    "部屋数",       # RM: 住宅あたりの平均部屋数
    "築年数",       # AGE: 1940年以前に建てられた持ち家の割合
    "距離",         # DIS: ボストンの雇用センターまでの加重距離
    "幹線道路アクセス",   # RAD: 幹線道路へのアクセスのしやすさ
    "固定資産税率",     # TAX: 1万ドルあたりの固定資産税率
    "生徒教師比",       # PTRATIO: 町ごとの生徒と教師の比率
    "黒人比率指数",     # B: 1000(Bk - 0.63)^2, Bkは町の黒人比率
    "低所得者率",       # LSTAT: 低地位の人口の割合(%)
    "住宅価格中央値",    # MEDV: 持ち家の中央値（1000ドル単位）
]
また、今回は 部屋数（RM） を特徴量として用い、住宅価格中央値（MEDV） を予測したい値（目的変数）として設定します。単回帰なので、特徴量は 1 つだけに限定しています。
# 特徴量と目的変数の設定（ここでは最初の 100 件を使う例）
X_train = df.loc[:99, ["部屋数"]]  # 特徴量：部屋数
y_train = df.loc[:99, "住宅価格中央値"]  # 目的変数：住宅価格中央値

 最小二乗法でパラメーターの最適化本コードでは、scikit-learn の LinearRegression を使用するため、実際に上記の計算手順を見ることはできません。しかし 内部的には同等のアルゴリズム（最小二乗法）を用いてパラメータを求めている と考えていただければ十分です。
学習データ X_train・y_train をもとにモデルを学習します。LinearRegression をインスタンス化し、fit メソッドを使って学習させています。
model = LinearRegression()  # 線形回帰モデル
model.fit(X_train, y_train)
fit で学習（パラメーターの最適化）が完了すると、最終的な 傾き と 切片 は次のように参照できます。
# パラメータ
print("傾き w1:", model.coef_[0])
print("切片 w0:", model.intercept_)
!傾きと切片
傾き（w1）は、「部屋数」が 1 増えたときに「住宅価格中央値」がどの程度上昇または下降するかを示す係数です。

切片（w0）は、「部屋数」が 0 のときに「住宅価格中央値」がどの値になるかを表す、いわゆる y 切片です（もちろん部屋数 0 の家は実際には考えにくいですが、あくまで数式上の意味合いです）。

 予測モデルを使って予測を行う方法として、model.predict() メソッドを使います。ここではグラフの描画のため、部屋数が最小値から最大値まで連続的に変化するとき に対応する住宅価格を予測し、その結果を線としてプロットしています。
# 学習データに対する予測値
print(model.predict(X_train))

# 可視化のための準備
plt.figure(figsize=(8, 4))
X = X_train.values.flatten()  # numpy配列にし、1次元に変換
y = y_train.values            # こちらもnumpy配列に変換

# グラフ用のX（部屋数）を最小値から最大値まで0.01刻みで作る
X_plt = np.arange(X.min(), X.max(), 0.01)[:, np.newaxis]
y_pred = model.predict(X_plt)

# 散布図 + 回帰直線の描画
plt.scatter(X, y, label="data")
plt.plot(X_plt, y_pred, label="LinearRegression")
plt.ylabel("Price in $1000s [MEDV]")
plt.xlabel("average number of rooms [RM]")
plt.title("Boston house-prices")
plt.legend(loc="upper right")
plt.show()
散布図 でプロットしているのは、学習データ内の「部屋数」と「住宅価格中央値」。
直線 でプロットしているのは、学習した回帰モデルに対して連続的な部屋数を入力したときの予測値。

 まとめここまで読んでいただきありがとうございました！

最近モデルを使った個人開発をしているので、気になったらお声掛けください！ご飯でも飯でも飲みでも！！
良かったらTwitterフォローしてねっ！

https://twitter.com/mi_01_24fu
日付	気温(°C)	販売数(本)
8月1日	32	201
8月2日	29	185
8月3日	34	198
8月4日	31	180
8月5日	35	209
変数名	詳細
CRIM	人口1人あたりの犯罪発生率
ZN	25000平方フィートを超える住居エリアの割合
INDUS	小売以外の商業用地が占める面積の割合
CHAS	チャールズ川沿い地域の有無を示すダミー変数（1: 該当、0: 非該当）
NOX	大気中のNOx濃度
RM	1940年以前に建てられた建物の割合
DIS	主要な5つの雇用施設までの距離
PAD	環状高速道路へのアクセスのしやすさ
TAX	1万ドルあたりの不動産税率の総額
PTRATIO	各町における児童と教師の比率
B	町毎の黒人比率を1000(Bk-0.63)^2で算出
LSTAT	低所得層に従事する住民の割合
MEDV	所有者が占有する住宅の中央値（単位: ＄1000）
はじめに

著者プロフィール

この記事を書いた背景

この記事で記載すること・しないこと

対象読者

線形回帰とは？

線形回帰を学ぶ前に、説明変数と目的変数について

具体例①：ビールの販売と気温

単回帰

重回帰

まとめ

単回帰を理解する前に、一次関数を理解する

温度が上がるとビールが売れる例で考える

人間が温度とビールの販売数を基に次の日の販売数を予測する場合

AIが温度とビールの販売数を基に次の日の販売数を予測する場合

ビール販売数の予測例

整理すると

パラメーター最適化の基礎概念

残差

モデルの指標評価

モデルのパラメーターの最適化

まとめ

単回帰の学習と予測

利用するデータセットについて

データセットの内容

学習データの読み込み

最小二乗法でパラメーターの最適化

予測

まとめ

Discussion
