決定木ってなんやねん(回帰木編)
はじめに
どもども、フリーランスエンジニアとして働いている井上弥風(いのうえみふう)です。
最近魚の飼育に凝ってまして、最初はネオンテトラを15匹だけ購入したつもりが、なぜか今55匹になってる今日この頃です。
もうハマりにハマっちゃって水槽の水でミニトマト育て始めちゃってます(クソ情報失礼しました)

著者プロフィール
私は元々バックエンド・インフラメインで仕事をしていて、AI周りの学習は2025年の2月に始めました。
とりあえずG検定・AWS AIF周りの試験勉強をして、何となく全体像を知った後、実際にXGBoostという決定木ベースのモデルで開発を始めました。
今もこのモデルで開発をしていて、あわよくば収益化を目指している(マジで可能性あると思っている領域なのでおもろい)のですが、やっぱり我流で進めているので色々と壁にぶつかってる、、、って状況です。
この記事を書いた背景
モデルを利用した開発でぶつかった内容を言語化することで知識をより定着させたいと思い、今回ぶつかったのが「決定木(回帰木)」だったので、そのまま記事にしました。
この記事で記載すること・しないこと
- 記載する内容
- 決定木に関する基礎概念
- 回帰木に関する基礎概念
- Pythonで決定木を動かす例
- 記載しない内容
- AIに関する基礎的な知識
- 統計学に関する基礎的な知識
- 分類木に関する基礎的な知識
対象読者
- 決定木の概要・回帰木の詳細について知りたい方
決定木とは何か?
まずは決定木とは何かという大枠から解説します。
決定木とは、「階層的な意思決定モデル」とも言え、複雑な意思の決定プロセスを木構造で表現した手法です。
データは最上部の「ルートノード」から入力され、各ノードで条件分岐が行われながら、最終的な分類結果や予測値を示す「葉ノード」へと進みます。
例えば、入力データとして「雨が降るか」や「風が強いか」といった情報を与えると、決定木はそれらの条件を順次評価し、最終的に「傘を持つべきかどうか」という判断を下す、といったイメージです。

決定木の構成要素
決定木は以下の要素から構成されます。
- ルートノード
- ツリーの一番上に位置する最初の分岐点
- ここからデータが入力され、最初の条件分岐が行われる
- 内部ノード
- ルートノードと葉ノードの中間に位置するノード
- 複数の条件分岐を経てデータが分類または予測される
- 葉ノード
- ツリーの末端に位置し、これ以上の分岐を行わず、最終的な予測値や分類結果を示すノード

if文との違いは?
プログラミング経験者なら薄々感じている方もいるかもしれませんが、決定木は基本的に条件分岐の仕組みを持つ点ではif文と似ています。
ただ、決定木とif文の大きな違いは「閾値や分岐の条件を誰が決めるか」という点にあります。
if文の場合
以下は、シンプルなif文の例です。
このコードでは、条件式はプログラマーがあらかじめ設定した固定の値や閾値に基づいて評価され、条件に応じて該当する後続処理が進んでいきます。
# 決定を格納する変数
decision = ""
# 「雨は降る?」という条件
if True:
# 「風は強い?」という条件
if False:
decision = "傘持たない"
else:
decision = "傘を持つ"
else:
# 「暑い?」という条件
if True:
decision = "日傘を持つ"
else:
decision = "傘持たない"
print("直接条件の結果:", decision)
もう少し現実的な話をすると、一般的なプログラミングの場合、例として動画配信サービスでは「利用者が課金しているかどうか」、クレジットカードの決済システムでは「不正利用かどうか」を、事前に設定した閾値や状態で判断し、適切な処理を実行します。
ここでポイントなのは、コード上に存在する条件や閾値はあくまで人間が決めた固定値という点です(処理によっては動的に閾値が決まる場合もありますが、その動的な値の範囲もあくまで人間の想定の範囲内)。
決定木の場合
決定木も同じく条件分岐を行いますが、その閾値を自動で最適化(いい感じの閾値を勝手に見つけてくれる)する点がif文との大きな違いです。
具体的には、与えられたデータセットに基づき、各ノードで数学的な基準(例:最小二乗誤差や情報利得)を用いて、どの分岐が最も予測精度を高めるかを自動的に判断し、最適な閾値を見つけ出します。
※具体的な詳細は後述するので、ここでは「最適化された閾値を自動で見つける」という点だけ覚えておけばokです^^
LLMはテキスト生成、CNNは画像解析、では決定木は何をする?
決定木は、大きく分けて「分類」と「数値予測(回帰)」の2つのタスクに用いられるアルゴリズムです。
決定木はChatGPTや画像生成AIのような直接的なユーザー向けのサービスとしてはあまり目立ちませんが、統計分析やデータサイエンスの現場では幅広く活用されています。
たとえば、ある企業が大量の顧客データから購買傾向を分析する場合、決定木は各顧客の属性に基づいて「購入するか否か」を分類するモデルとして利用できます。
また、経済指標や気象データを用いて将来の売上や気温を予測する場合にも、数値予測の手法として決定木が役立ちます。
つまり、表にはあまり登場しないけど縁の下の力持ち的なツールの訳ですね^^
回帰木と分類木
決定木にも、「回帰木(かいきぎ)」と「分類木(ぶんるいぎ)」という二種類のアルゴリズムが存在します。
一つ一つ見ていきましょう。
回帰木の特徴
回帰木は、連続的な値の予測に特化した回帰モデルです。
ここでいう「連続的な値」とは、整数(0, 1, 2, 3...)やカテゴリ(赤・青・黄色...)のように離散的な値ではなく、1.01, 1.02 のように非常に細かく変化し、理論上は無限に中間値を取ることができる値を指します。
つまり、回帰木は過去のデータから得られるパターンをもとに、数値の微妙な変動をも捉え、細かい単位での予測を行うことが可能なモデルです。
たとえば、これまでの地球温暖化のデータを利用して将来の気温上昇を予測する場合、回帰木は連続した温度データから「どの程度上昇するか」を分析して結果を算出したりすることができます。

分類木の特徴
分類木は、与えられた特徴量に基づき、対象データがどのカテゴリに属するかを判断するためのモデルです。
例として、あるメールの本文や送信元情報などの複数の特徴から「スパム」か「非スパム」かを自動で判定する、といった用途に用いられたりします。

適用分野・使い分け
決定木を用いる場合、その目的となる予測の種類によって回帰木・分類木の使い分けがされます。
- 数値予測(回帰)を行いたい場合
- 住宅の価格予測、○○年後の温暖化予測、会社の将来の収益予測など、具体的な数値を求めるケースには回帰木が適している
- カテゴリ分け(分類)を行いたい場合
- メールがスパムかどうか、不正利用の有無、顧客の購買行動の有無など、2値または複数のカテゴリに分類する問題では分類木が適している
つまり、予測対象が「連続値かカテゴリか」によって、回帰木と分類木を使い分ける訳ですね。
【単一特徴量で体験】回帰木はどうやって分岐点を探すのか?
記事の前半で「決定木は閾値を自動で決める」と記載しましたが、実際どのようにしてその自動調整が行われるのでしょうか?
ここからは、単一の特徴量を例に、回帰木がどのようにして最適な分岐点(閾値)を見つけ出すのかを詳しく解説して行きます。
回帰木の分岐点を探す前に、「データのバラつき」を理解する
まず前提として、回帰木は各ノードでデータを条件に従って分割し、最終的な予測値を導き出す仕組みです。
図のように、ノードが次々と枝分かれすることで、複雑なデータ構造をモデル化していきます。

各ノードが枝分かれする箇所というのは、つまり「条件分岐が行わている箇所」に相当し、決定木は「データを自動で最適な閾値に基づいて分割する」ことで、より精度の高いモデルを作り上げます。
分割の基本原則は、「分割後のデータのバラつきが最小になる」点を選ぶことです。
ただ、そもそも「バラつきが最小」という言葉自体が若干抽象的なので、まずは「バラつきとは何か」を解説していきます。
データのバラつきとは何か、バラつきの最小値とは何かを理解した上で、各ノードがどのように分岐していくのかを見ていきましょう^^
「データのバラつき」をイメージするための例
ここでは、車販売の例を使って「平方和(バラつきを意味する値)」という指標を理解していきます。
例として、ある車販売会社には、「営業1課」と「営業2課」の2つの課があり、それぞれ5人ずつ、合計10人の営業担当がいるとします。各担当の販売台数は以下のとおりです。
営業1課
| 営業さん | 販売台数 |
|---|---|
| Aさん | 4台 |
| Bさん | 0台 |
| Cさん | 1台 |
| Dさん | 3台 |
| Eさん | 2台 |
営業2課
| 営業さん | 販売台数 |
|---|---|
| Fさん | 2台 |
| Gさん | 3台 |
| Hさん | 2台 |
| Iさん | 2台 |
| Jさん | 1台 |
ではここで、営業部長に1課と2課の販売成績を報告しなければいけないことになりました。
1課の販売成績の平均は以下ですね。
2課の成績は以下になります。
平均だけを見ると、両課とも「2台」という同じ成績に見えますが、このままでは以下のような問題が発生するかもしれません。
- 個々の実績が見えにくい
- 1課のAさんは4台売っているにもかかわらず、平均値「2台」で評価され、個々の頑張りが反映されない
- 「俺もう会社辞める!!」状態になるかもしれない...omg
- 1課のAさんは4台売っているにもかかわらず、平均値「2台」で評価され、個々の頑張りが反映されない
- 改善点が不明瞭
- 成績不振のBさん販売台数は0台だが、全体の平均に隠れてしまい、もしかすると改善できるかもしれないのにそれが見えない
これを解決するのが、平方和です。

平方和の目的
平方和の目的は「データのバラつき具合を数値化するもの」です。
平均では表現できないものを平方和では表現できるわけです。
いきなり言われても「データのバラつきを数値化??」って感じなので、とりあえず実際にやってみましょう。
平方和の求め方と利用シーン
まず、平方和の求め方が以下です(数式アレルギーの方、意外とやってることは簡単なのでご安心を!)
ここでは、先ほど紹介した例の1課と2課の平均がどちらも「2」であったことを利用して、平方和を求めてみます。
では、1課の平方和を求めていきましょう。
次に、2課の平方和を求めていきましょう。
各課の平方和を整理すると、以下のようになります。
- 1課の平方和
- 10
- 2課の平方和
- 2
ここまでが平方和の求め方であり、「バラつきとは何か?」に対する解説です。
極端な例を出すと、各データが離れている(1と100と50000と60000000...)場合、平方和は大きくなるし、各データが近い(1と2と2と1と3...)の場合は平方和が小さいという事ですね。
その上で、以下の内容が理解できていればokです^^
- 平方和が大きい = 各データに差がある
- 平方和が小さい = 各データが大体同じ数
より詳しく知りたい方は以下の記事を参考にしてみてください^^
決定木を理解する上では、バラつきに関してはここまでの内容が理解できていれば問題ありません^^
データセットと散布図
では、データのバラつきを意味する平方和を理解した上で、「回帰木はどうやって分岐点を探すのか?」という部分を深掘りしていきます。
回帰木がどのように分岐点を探すのかを理解しやすいように、今回は例として「温度によってアイスの販売数が変わる」という例で話を進めます。
まず、下記が過去のアイスの販売数と温度がペアになったデータセットです。
| No | 温度 | アイスの販売数 |
|---|---|---|
| 1 | 10.0 | 0 |
| 2 | 13.0 | 1 |
| 3 | 18.0 | 2 |
| 4 | 22.0 | 5 |
| 5 | 21.5 | 4 |
| 6 | 22.5 | 6 |
| 7 | 24.5 | 8 |
| 8 | 26.0 | 9 |
| 9 | 26.5 | 10 |
| 10 | 30.0 | 12 |
| 11 | 33.5 | 13 |
| 12 | 35.0 | 14 |
| 13 | 36.5 | 15 |
| 14 | 39.0 | 8 |
| 15 | 41.0 | 4 |
| 16 | 42.5 | 3 |
| 17 | 43.5 | 1 |
| 18 | 44.5 | 0 |
内容はそんなに難しいものではなく、単にその日の温度と、アイスの販売数がペアで存在するだけですね。
下記がその散布図です。
何となく、温度が上がるにつれてアイスの販売数も上がっていることが分かりますね(縦がアイスの販売数・横が温度)。
ただ、逆に熱中症注意報が発令されるようなレベルになると販売数が下がっている事も見て取れます。

SSE(平方和)の求め方
では、さっそくSSE(これ以降、平方和の事をSSEと呼びます)を求めて回帰木の分岐点を探していきます(なぜSSEを求める事 = 分岐点を探すことになるのかは後述)。
ここではアイスの販売データを用いて、実際にSSEを求める手順を確認していきます。
まず、下記が温度とアイスの販売数のペアが記載されたデータですね。
| No | 温度 | アイスの販売数 |
|---|---|---|
| 1 | 10.0 | 0 |
| 2 | 13.0 | 1 |
| 3 | 18.0 | 2 |
| 4 | 22.0 | 5 |
| 5 | 21.5 | 4 |
| 6 | 22.5 | 6 |
| 7 | 24.5 | 8 |
| 8 | 26.0 | 9 |
| 9 | 26.5 | 10 |
| 10 | 30.0 | 12 |
| 11 | 33.5 | 13 |
| 12 | 35.0 | 14 |
| 13 | 36.5 | 15 |
| 14 | 39.0 | 8 |
| 15 | 41.0 | 4 |
| 16 | 42.5 | 3 |
| 17 | 43.5 | 1 |
| 18 | 44.5 | 0 |
下記がデータの散布図ですね。

1. グループ分けしてSSEを計算する
まず、散布図の左端に位置する1つ目のデータをグループA、残りをグループBと分けて考えます。
単純に、下記図の赤線の左の1つのデータがグループA・それ以外がグループBというだけです。

次に、SSEの求め方を思い出してみましょう。
ですね。
SSEの求め方を思い出したうえで、「各販売数 - 販売数の平均」の二乗を足し合わせて、各グループのSSEを求めます。
まず、グループAのSSEを求めます。
- グループAのデータ数が1個
- グループAの平均販売数は0
- (0−0)²= 0 → グループAのSSE = 0
続いて、グループBのSSEを求めます。
- グループBのデータ数が17個
- グループBの平均販売数は6.76
- 個々データの販売数と6.76との差を二乗して合計すると、グループBのSSE = 373.0588…
- ※やっていることはグループAと同じで、データ数が多いだけ
最後に、グループAとグループBのSSEを足します。
現在は何をしているかがあまりわからなくても大丈夫なのですが、一回目のSSEの計算結果は373.0588でした。
一回目の計算をパターン1(グループAがNo1, グループBがNo2 ~ 18)と呼びます。
続いて、二回目の計算、つまりパターン2(グループAがNo1 ~ 2, グループBがNo3 ~ 18)を実施してみます。
パターンBでは、グループAとグループBに属するデータが若干変わります。
具体的には下記図のように、グループの分かれ目が一つ右にシフトします。

では、グループAとグループBのSSEを再度求めていきます。
まず、グループAのSSEを求めます。
- グループAのデータ数が2個
- グループAの平均販売数は0.5
- (0 − 0.5)² + (1 - 0.5)² = 0.25 + 0.25 = 0.5 → グループAのSSE = 0.5
続いて、グループBのSSEを求めます。
- グループBのデータ数が16個
- グループBの平均販売数は7.125
- 個々データの販売数と7.125との差を二乗して合計すると、グループBのSSE = 337.75
最後に、グループAとグループBのSSEを足します。
では、パターン1のSSEとパターン2のSSEを整理してみましょう
- パターン1
- SSE = 373.0588
- パターン2
- SSE = 338.25
この流れで、パターン3, 4 ... 16, 17...と全パターンのSSEを求めていきます。
やることは全く一緒で、パターン3の時はデータの三つ目で線を区切り、17の場合はデータの17個目でデータを区切って、各SSEを求めるだけです。
パターン3の場合

.
.
.
パターン17の場合

各パターンごとで求めたSSEを整理すると以下のようになります。
| i | SSE(A) | SSE(B) | SSE(A)+SSE(B) |
|---|---|---|---|
| 1 | 0.0000 | 373.0588 | 373.0588 |
| 2 | 0.5000 | 337.7500 | 338.2500 |
| 3 | 2.0000 | 309.7333 | 311.7333 |
| 4 | 14.0000 | 303.2143 | 317.2143 |
| 5 | 17.2000 | 288.9231 | 306.1231 |
| 6 | 28.0000 | 284.9167 | 312.9167 |
| 7 | 49.4286 | 284.9091 | 334.3377 |
| 8 | 73.8750 | 284.0000 | 357.8750 |
| 9 | 102.0000 | 279.5556 | 381.5556 |
| 10 | 146.1000 | 259.5000 | 405.6000 |
| 11 | 194.5455 | 221.7143 | 416.2597 |
| 12 | 248.0000 | 154.8333 | 402.8333 |
| 13 | 307.0769 | 38.8000 | 345.8769 |
| 14 | 307.2143 | 10.0000 | 317.2143 |
| 15 | 319.6000 | 4.6667 | 324.2667 |
| 16 | 337.7500 | 0.5000 | 338.2500 |
| 17 | 373.0588 | 0.0000 | 373.0588 |
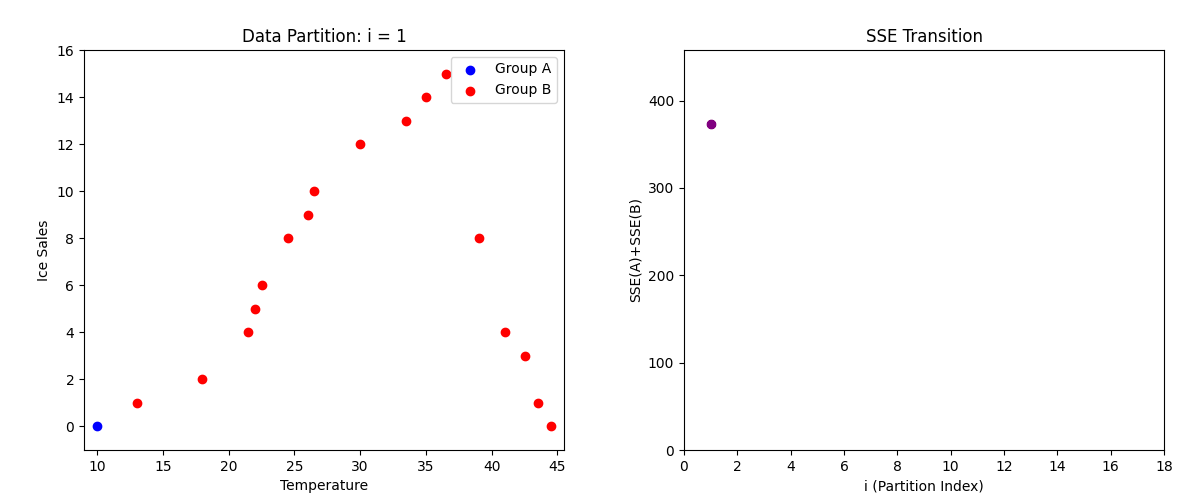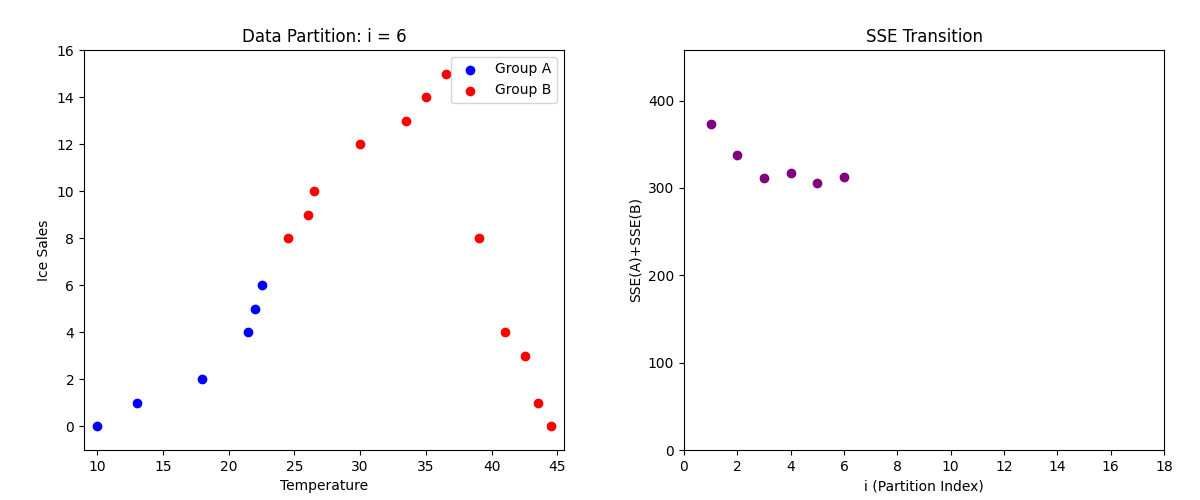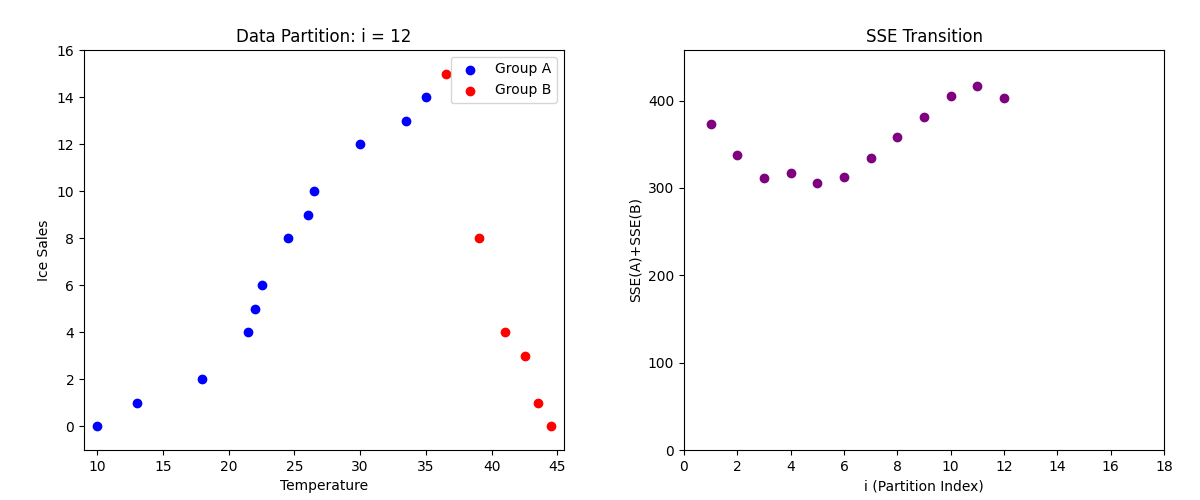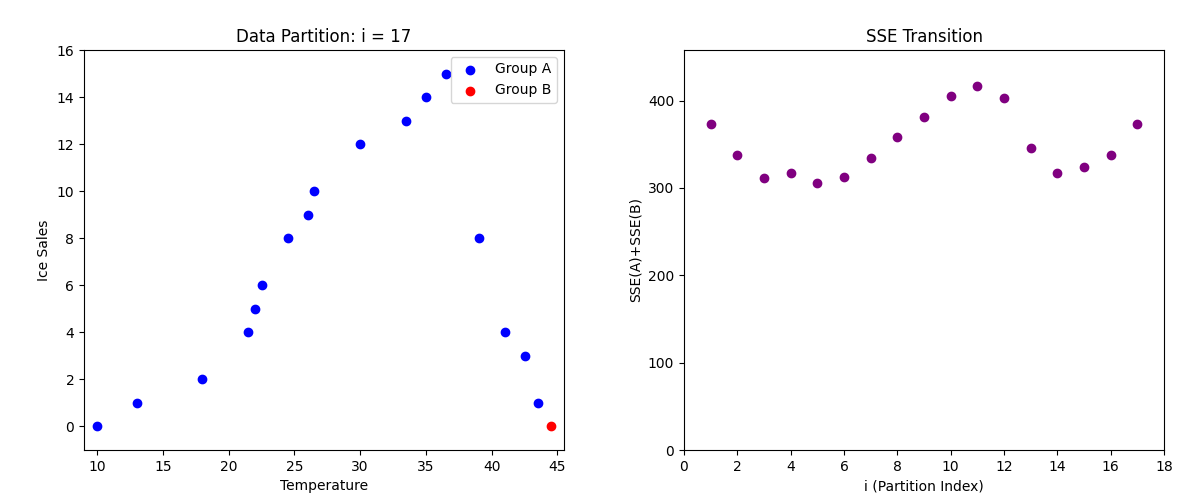
下記は左側が各データの散布図で、パターン(1回目、二回目、三回目...)ごとに色が変わっています。
また、右側の散布図は各パターンで求めたSSEをプロット(点を打った)したものです。
何をしているのかを整理する
ここまでいろいろと計算してきましたが、そもそも「なぜこんなふうにグループを分割して、SSEを求めているのか」を整理していきます。
-
グループ分け → グループごとのバラつきを測るため
- 各グループごとにSSEを計算しているのは、「グループ内のバラつき」を知るためです。
- バラつき(=データ同士の距離感)が大きいとは、つまり平均から遠いデータが多いということ。
- 逆にバラつきが小さいとは、平均付近にまとまっているデータが多いということ。
-
SSEが「バラつき」を数値化する
- SSEが大きければ大きいほど、「平均からのズレ」が大きいデータが多いということ。
- SSEが小さければ小さいほど「平均からのズレ」が小さく、データがまとまっているということ。
-
複数グループのバラつきの合計を求める理由
- その上で、データをAとBに分けた場合、どちらのグループもなるべく「まとまりが良い(バラつきが小さい)状態」を目指すことが、決定木の分岐において重要なのです。
- そのために、グループAのSSEとグループBのSSEを合計して「バラつきの合計」を見ています。両方のグループのバラつきが少ないほど、データ全体としても効率的な分割ができていると判断できるわけです。
このように見てみると、やっていることは
- データをある位置で区切ってグループAとグループBに分ける
- それぞれのSSEを計算する(=各グループがどれだけバラついているか)
- SSE(A)+SSE(B)の合計が最も小さくなる位置を探す
という流れに過ぎないわけですね。結果的に、
- SSE(A)+SSE(B) が小さいほど、「AとBどちらのグループもまとまり」が良い(=平均付近にデータが集まっている)
- SSE(A)+SSE(B) が大きいほど、「AかBのどちらか、あるいは両方のグループでデータが散らばっている」
という解釈ができる訳です。

「パターン1」「パターン2」「パターン3」…と区切る場所をずらしながら、このSSE(A)+SSE(B)をすべて比べることで、「一番バラつきが小さくなる分割ポイント」を探していたんですね。
ちなみに、各パターンで算出したSSEを散布図で表すと以下のようになります。

そして、パターンごとで算出したSSEの中で最小のSSEは5パターン目になります。

これが何を意味しているかと言うと、グループごとにデータを分割した際に、「全パターンの中で、このグループAとBが一番データのバラつきが少ない」ということを意味します。
各パターンでSSEを算出した結果、最小SSEが分かった、じゃあどうするの?
各パターンでSSEを計算して、最小SSEは分かりました。
| i | SSE(A) | SSE(B) | SSE(A)+SSE(B) |
|---|---|---|---|
| 1 | 0.0000 | 373.0588 | 373.0588 |
| 2 | 0.5000 | 337.7500 | 338.2500 |
| 3 | 2.0000 | 309.7333 | 311.7333 |
| 4 | 14.0000 | 303.2143 | 317.2143 |
| 5 | 17.2000 | 288.9231 | 306.1231 |
| 6 | 28.0000 | 284.9167 | 312.9167 |
| 7 | 49.4286 | 284.9091 | 334.3377 |
| 8 | 73.8750 | 284.0000 | 357.8750 |
| 9 | 102.0000 | 279.5556 | 381.5556 |
| 10 | 146.1000 | 259.5000 | 405.6000 |
| 11 | 194.5455 | 221.7143 | 416.2597 |
| 12 | 248.0000 | 154.8333 | 402.8333 |
| 13 | 307.0769 | 38.8000 | 345.8769 |
| 14 | 307.2143 | 10.0000 | 317.2143 |
| 15 | 319.6000 | 4.6667 | 324.2667 |
| 16 | 337.7500 | 0.5000 | 338.2500 |
| 17 | 373.0588 | 0.0000 | 373.0588 |

じゃあどうするのかと言うと、このSSEの最小値のポイントで決定木を分割します!

なぜSSEの最小の箇所が最初の分岐点になるのか?
じゃあどうするのかと言うと、このSSEの最小値のポイントで決定木を分割します!
これはどういう事でしょうか?
結論から言えば、SSEが最小になる地点での分割は、つまり「両グループのバラつきが最小にっている地点」なのです。
改めて説明しますが、バラつきが小さいグループは、似たデータ同士がまとまっている状態を意味します。
その上で、決定木はこうした分岐を繰り返しながら、最終的に「もっとも類似したデータだけが集まった」葉ノードにたどり着かせるのが狙いです。
決定木の分岐のイメージ
決定木はデータに対して複数の条件分岐(true or false, 5以上, 5未満など)を積み重ね、最終的な出力を導きます。最初の分岐でSSEが最小となるポイントを選ぶことで、初期段階から「似通ったデータ同士」を一括りにし、その後の分岐を効率よく進められます。

たとえ話:コンサートの警備員の場合
例えば、あなたがコンサート会場の警備員で、以下のようなルールで観客を誘導するとします。
- 20~40歳 → 立ち見席
- 41~60歳 → 座り見席
このとき、最初に「40歳以下か、それとも41歳以上か」だけを尋ねれば、すぐにそれぞれの席へ導くことが可能ですね。
もし最初に「20~30歳か、それ以外か」を聞いたあと、「40~60歳か、それ以外か」をまた聞く…といった細かな質問を繰り返すと、時間もかかり、手間も増えてしまいます。
決定木も同様で、はじめの分岐で大まかに似た属性の人たちを分けることができれば、その後の分岐(ノード)でさらに細かく分割していくのがスムーズになります。
逆に、最初の分岐が適当だと、後の工程で無駄に細かい質問を繰り返したり、似ていないデータが混ざったままになったりして、最終的な精度が下がりがちな訳ですね。

まとめると、SSEが最小化されるポイントを最初に分岐点に選ぶことで、「グループ内のバラつきが小さい(=似た傾向のデータを集められる)」状態を作り出せます。
あとはこのプロセスを繰り返すことで、より細かい部分まで最適化され、最終的に精度の高い決定木が得られるのです。
分岐を繰り返していく
では、SSEの最小値を求めたことで、以下のような決定木が作成できました。

しかしこれではまだ最終的な決定木の形ではありません。
何故かというと、ルートノードから伸びる右側のノードは、データ数が13個もあります。
また、13個のデータのバラつきを見てみると、以下のようなバラつきが確認できます。

※下記が全データが含まれた散布図

決定木は、過去のデータを基に適切な箇所でノードを分割し、最終的な木構造を決定します。

つまり、現状はバラつきの多いデータが1グループになってしまっているため、これでは正しい予測ができないわけですね。
そのため、残ったデータ13個を基に再度SSEを求め、ノードを分割していきます。
と言ってもやることは今までと全く同じで、13個の中でSSEを求め、最小値のデータでノードを分割する、、、というのを繰り返していくだけです。
最終的な回帰木の構造
では、13個のデータが存在するノードを分割し、さらにその先で必要に応じて分割を繰り返した場合、最終的にどういった決定木になるのでしょうか?
※今回は最低サンプル数を5にします。つまり、各ノードでデータ数が5以下の場合、データの分割をストップします(過学習防止と、あまり複雑にすると理解が難しくなってくるため)。
結果が以下です。

元のデータの散布図をノード単位で区切ると以下のようになります

まとめ
実際の決定木はそもそものデータ数がより多く、かつ決定木の深さも幅も広くなりますが、決定木がどのように各ノードの分岐ポイントを見つけるか、そして最終的にどういった木構造になるかはここまででお話しした通りです。
この出来上がった決定木に対して、例えば「温度10℃」をモデルの入力として入れると、売れるであろうアイスの販売数として「2.4」を出力します。
また、温度が40℃以上の場合は2.0を返すわけですね
※ここまで単純な出力にはなりませんが、イメージはこの通りです。

さて、今まで学んできた内容はあくまで特徴量が「一つの場合」でした。
では、特徴量が複数ある場合、決定木の各ノードはどのように分割されていくのでしょうか?
詳しく見ていきましょう。
【多次元へ拡張】複数の特徴量がある場合の回帰木アルゴリズム
ではでは、特徴量が複数ある場合、決定木の構造はどうなるのでしょうか?閾値はどう決まっていくのでしょうか?
実際には、特徴量が一つの場合と基本的な仕組みは同じです。
詳しく見ていきましょう。
データセットと散布図
まず、下記のデータがあるとします。
| No | 温度 | アイスの販売数 | 湿度(%) | 人口 |
|---|---|---|---|---|
| 1 | 13.0 | 0 | 76 | 50 |
| 2 | 15.0 | 1 | 74 | 52 |
| 3 | 18.0 | 2 | 71 | 55 |
| 4 | 22.0 | 5 | 70 | 60 |
| 5 | 22.0 | 4 | 70 | 58 |
| 6 | 22.5 | 6 | 69 | 62 |
| 7 | 24.5 | 8 | 78 | 64 |
| 8 | 26.0 | 9 | 68 | 67 |
| 9 | 26.5 | 10 | 67 | 70 |
| 10 | 31.0 | 12 | 60 | 75 |
| 11 | 32.5 | 13 | 53 | 80 |
| 12 | 34.0 | 14 | 50 | 85 |
| 13 | 36.5 | 15 | 47 | 90 |
| 14 | 38.0 | 8 | 42 | 88 |
| 15 | 41.0 | 4 | 38 | 85 |
| 16 | 42.5 | 3 | 35 | 82 |
| 17 | 42.5 | 1 | 33 | 78 |
| 18 | 44.5 | 0 | 31 | 75 |
以下が温度とアイスの関係を図にした散布図です。
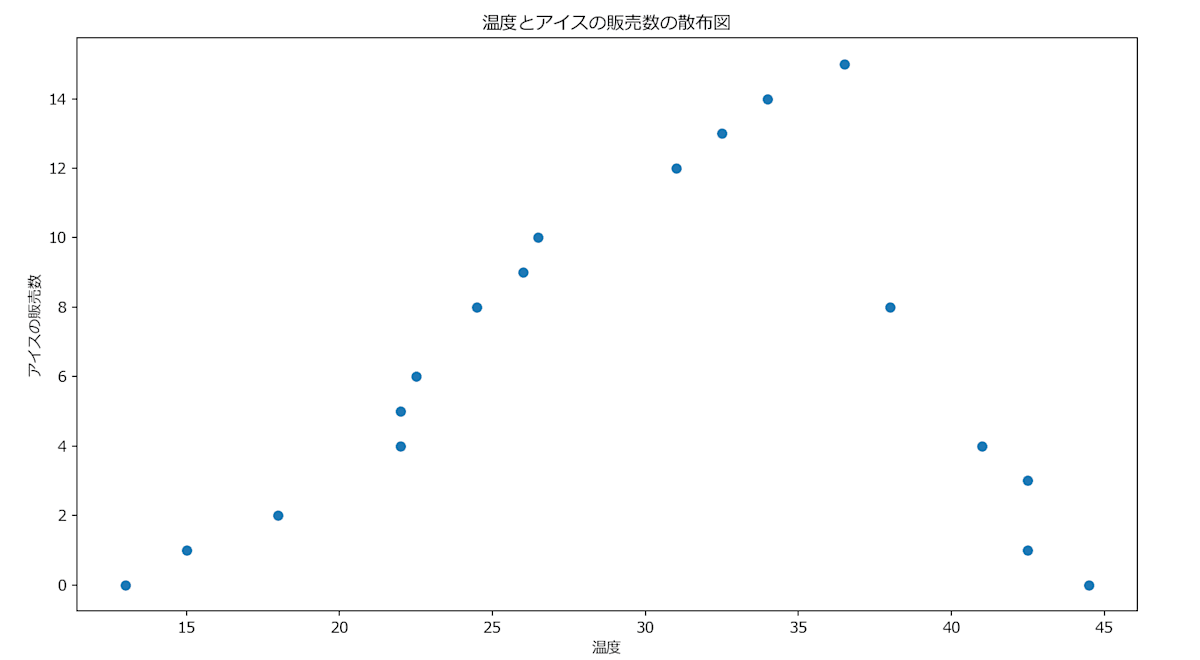
以下が湿度とアイスの関係を図にした散布図です。

以下が人口とアイスの関係を図にした散布図です。

複数の特徴量がある際にノードを分割していく仕組み
では、三つの特徴量を基に最適な決定木を作成していきます。
流れは以下の通りです。
- 各特徴量で最小SSEを求める
- 全特徴量の中で最小のSSEで、ノードを分割する
具体的に手順を見ていきましょう。
まず、特徴量として存在する温度・湿度・人口の各SSEを計算していきます。
流れは特徴量が一つの時と同じで、No1とNo2 ~ 18のSSEを計算して、それを足す、次はNo1 ~ 2とNo3 ~ 18でSSEを計算して、それを足す、、、というのを繰り返すだけです。
ただ、特徴量が一つの時と違うのはこの計算を特徴量全てで行うという点ですね。
実際に計算した結果が以下です。
| 温度 | 湿度 | 人口 |
|---|---|---|
 |
 |
 |
 |
 |
 |
若干見にくいですが、三つの特徴量の中で最小のSSEは人口で、「305.607」でした。
各特徴量のSSEの散布図はこちら
温度

湿度

人口
 |
|
ではどうするのか?まずは人口で分割するわけです。

なぜ最小SSEで分けるのかを覚えていますか?
それは「最小SSEとはデータのバラつきが一番小さいことを意味しており、そこで分けるのが左右のグループ間でも一番データが近しい状態でまとまっているから」ですね^^
ノードの分割を繰り返す
では、続いて人口からどのようにノードを分けていくのか、です。
これはもう今までやってきたことの連続です。
つまり、ノードに含まれるデータ内で再度最小SSEを求め、そこでノードを分割していくわけですね。
今回は文章量が長くなってしまうため最後まで最小SSEは求めませんが、ノードの分割を繰り返す途中では下記のようになるかもしれませんし、

最終的にはこんな感じになるかもしれませんね^^

まとめ
いかがでしたでしょうか?
特徴量がいくら増えても、最小SSEを求めて、そこでノードを分割する、という流れは特徴量が一つの場合と変わらないことが分かったかと思います。
では最後に、Pythonで実際に決定木を触ってみて、コードベースでの理解を深めていきます。
回帰木をPythonで動かしてみる
ではここから、実際にPythonを利用して決定木モデルを動かしていきます。
利用するデータセットについて
今回利用するのは「住宅価格」に関するデータセットです。
具体的には、ボストン近郊の住宅情報と価格に関するデータです。
※ちなみに、この「住宅価格データセット」はカリフォルニア大学アーバイン校が無償で提供してくれているデータセットです。
データセットの内容
データセットの内容は以下です。
| 変数名 | 詳細 |
|---|---|
| CRIM | 人口1人あたりの犯罪発生率 |
| ZN | 25000平方フィートを超える住居エリアの割合 |
| INDUS | 小売以外の商業用地が占める面積の割合 |
| CHAS | チャールズ川沿い地域の有無を示すダミー変数(1: 該当、0: 非該当) |
| NOX | 大気中のNOx濃度 |
| RM | 1940年以前に建てられた建物の割合 |
| DIS | 主要な5つの雇用施設までの距離 |
| PAD | 環状高速道路へのアクセスのしやすさ |
| TAX | 1万ドルあたりの不動産税率の総額 |
| PTRATIO | 各町における児童と教師の比率 |
| B | 町毎の黒人比率を1000(Bk-0.63)^2で算出 |
| LSTAT | 低所得層に従事する住民の割合 |
| MEDV | 所有者が占有する住宅の中央値(単位: $1000) |
また、実際に下記URLでブラウザからでもアクセスできます。
↓こんな感じ

今回は各データの詳細は説明しないのですが、簡単に言うとこのデータセットはボストン近郊の506地区ごとのデータを一レコードずつに格納しているわけですね。
まあ各地区の治安とか築年数とかの情報って感じです。
データセットの読み込み
まずは、学習データとしてボストン住宅価格データセットを読み込みます。以下のコードで、データを取得して前処理を行っています。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor, plot_tree
# データセットの読み込み
df = pd.read_csv(
"https://archive.ics.uci.edu/ml/machine-learning-databases/housing/housing.data",
header=None,
sep="\\s+",
)
df.columns = [
"犯罪率", # CRIM: 町ごとの犯罪発生率
"大規模住宅地率", # ZN: 25,000平方フィート以上の住宅地の割合
"非小売業率", # INDUS: 非小売業が占める土地の割合
"チャールズ川ダミー", # CHAS: チャールズ川沿いなら1、そうでなければ0
"窒素酸化物濃度", # NOX: 窒素酸化物濃度(10ppmあたり)
"部屋数", # RM: 住宅あたりの平均部屋数
"築年数", # AGE: 1940年以前に建てられた持ち家の割合
"距離", # DIS: ボストンの雇用センターまでの加重距離
"幹線道路アクセス", # RAD: 幹線道路へのアクセスのしやすさ
"固定資産税率", # TAX: 1万ドルあたりの固定資産税率
"生徒教師比", # PTRATIO: 町ごとの生徒と教師の比率
"黒人比率指数", # B: 1000(Bk - 0.63)^2, Bkは町の黒人比率
"低所得者率", # LSTAT: 低地位の人口の割合(%)
"住宅価格中央値", # MEDV: 持ち家の中央値(1000ドル単位)
]
# 特徴量と目的変数の設定
X_train = df.loc[:99, ['部屋数']] # 特徴量に100件のRM(平均部屋数)を設定
y_train = df.loc[:99, '住宅価格中央値'] # 正解値に100件のMEDV(住宅価格)を設定
また、今回は 部屋数(RM) を特徴量(説明変数)として用い、住宅価格中央値(MEDV) を予測したい値(目的変数)として設定します。
モデルの作成と学習
続いて、モデルにデータを学習させていきます。
# 深さ2の回帰木モデルの作成・学習
model = DecisionTreeRegressor(
# squared_error: 平均二乗誤差で、つまり今まで求めていたSSEと同じ手法を利用するという設定
criterion="squared_error",
# 木の深さを指定する。「2」の場合は「ルートノードを除いて」、二つの層を持った木を作成することを意味する
max_depth=2,
# 最小サンプル数を指定する。小さければ小さいほど、木の深さが大きくなり、過学習を起こしやすい。ただ、その分予測が正確になる場合もあるので、調整が必要。
min_samples_leaf=1,
)
model.fit(X_train, y_train)
決定木の可視化
続いて、決定木を可視化してみます。
# 決定木の可視化 (plot_tree を使用)
plt.rcParams["font.family"] = "Meiryo"
plt.figure(figsize=(10, 8))
plot_tree(model, feature_names=["部屋数"], filled=True)
plt.show()
上記を実行した結果が以下です。

samplesはノードに含まれるデータの数だったりするので、その他にも気になる点があれば色々と調べてみてください^^
散布図とノード分割位置の可視化
# データと予測値の可視化
plt.figure(figsize=(8, 4)) # プロットのサイズ指定
X = X_train.values.flatten() # numpy配列に変換し、1次元配列に変換
y = y_train.values # numpy配列に変換
# Xの最小値から最大値まで0.01刻みのX_pltを作成し、2次元配列に変換
X_plt = np.arange(X.min(), X.max(), 0.01)[:, np.newaxis]
y_pred = model.predict(X_plt) # 住宅価格を予測
# 学習データ(平均部屋数と住宅価格)の散布図と予測値のプロット
plt.scatter(X, y, color="blue", label="data")
plt.plot(X_plt, y_pred, color="red", label="DecisionTreeRegressor")
plt.ylabel("Price in $1000s [MEDV]")
plt.xlabel("average number of rooms [RM]")
plt.title("Boston house-prices")
plt.legend(loc="upper right")
plt.show()
実行結果が以下です。

このグラフは、横軸が「平均部屋数(RM)」、縦軸が「住宅価格の中央値(千ドル単位)」を示しています。
- 青い点(散布図)
- ボストンの各地域で実際に観測された「平均部屋数」と「住宅価格中央値」の対応を表しています。点がばらついているのは、地域ごとに住宅価格や部屋数が異なるためです。
- 赤い線(決定木回帰の予測値)
- 回帰木モデルが、平均部屋数をもとに住宅価格を予測した結果を示しています。決定木が特徴量(ここでは平均部屋数)の値によってデータを区切り、それぞれの区間で一定の値を出すため、階段状の形になっているわけです。
つまり、この図からは、
- 実際のデータ(青い点)の分布状況
- 決定木がどのように「平均部屋数」をいくつかの区間に分割して、それぞれの区間でどのような住宅価格を予測しているか
などが分かるわけですね。
まとめ
ちょっと記事を大きくし過ぎました!
普通に本にした方が私も読者も楽だったのでは、と今更ながら感じています...w
私は普段決定木ベースのモデル(LightGBM・XGBoost)などで開発をしているのですが、やっぱり詰まる時があります。
そのたびに仕組みを理解して、言語化して、記事にして~を繰り返すわけではないですが、外部の人向けに説明しようとすると体系的に、かつ具体的に書かないといけないので、理解度はダンチですね。。
長々と呼んでくださった方、ありがとうございました!
良かったらTwitterフォローしてねっ!
Discussion