🌊

球体上に波エフェクトを実装する

2024/06/11に公開

Unity

shader

effect

tech

はじめに

動作サンプル

上記のようなエフェクトをプロジェクトで作成する機会があり、いくつか発見があったのでそれを紹介しつつ、実装方法を解説していきたいと思います。

なお、ここで解説している実装は以下のGitHubのリポジトリにアップしてあるので、詳細は合わせてこちらも確認ください。

コンセプトと実装方針

まずは全体を俯瞰する意味で、実装方針とそのコンセプトについて解説します。

コンセプト

まずコンセプトは、シャボン玉のような球体を使ってエリアを表現することでした。そして触れた際に、触れた位置を中心として波紋が広がるようにするというものです。
しかし普通のシャボン玉の儚さよりは強さを感じさせつつ、触れた際にアニメーションさせることが目的でした。

実装方針

実装方針はまず、色味の表現としてノイズの重なりを利用してシャボン玉のようなゆらゆらした演出を実現しようと考えました。また波紋については、球体の中心から触れた位置へ向かうベクトルを軸として、そこを中心に球体状に波紋を広げるようにしました。平面であれば任意の点からの距離を入力に sin 関数を利用して波表現ができますが、今回は球体のため任意の点から円周に沿って離れた距離を入力とする方針としました。

実装解説

さっそく実装について解説していきましょう。

色のブレンド

まず最初に見ていくのは色のブレンドです。まずはコードを見てみましょう。

色のブレンド計算

// ノイズの広がりを調整するためドーム表面のエフェクトのUV位置を拡大して調整する
i.uv *= 8.5;

// 色のブレンド処理
fixed4 col = 0.0;

float d1 = fbm(i.uv + _Time.xy * 0.22, 2);
float d2 = fbm(i.uv - _Time.xy * 0.33, 2);
float d3 = fbm(i.uv + _Time.xy * 0.40, 2);

float t1 = smoothstep(0.1, 0.35, d1 * d2);
float t2 = smoothstep(0.1, 0.25, d1 * d3);
float t3 = smoothstep(0.1, 0.25, d2 * d3);

col = lerp(_Color1, _Color2, t1);
col = lerp(col, _Color3, t2);
col = lerp(col, _Color4, t3);

fbm関数の実装

fbmは Fractal Brownian Motion - 非整数ブラウン運動 の頭文字で、ノイズ関数を、周波数を変えて複数足し合わせることで実現する雲模様のような見た目を生成する方法です。

fbmについては以下の記事が詳しいです。
https://thebookofshaders.com/13/?lan=jp

実際の実装は以下のようになっています。

a が amplitude 、st が frequency を表しています。ループが繰り返されるたびに振幅（ amplitude ）が半分になっていき、最終結果 v に足しこまれています。

float fbm(in float2 st, int octave)
{
    float v = 0.0;
    float a = 0.5;

    for (int i = 0; i < octave; i++)
    {
        v += a * noise(st);
        st = st * 2.0;
        a *= 0.5;
    }

    return v;
}

今回利用したのはシンプルなパーリンノイズです。パーリンノイズは領域を格子状に分割し、その中でベクトルの計算を行ってランダム性を計算するものです。詳細については以前に個人ブログに書いたことがあるので、興味がある人はそちらをご覧ください。

float noise(in float2 st)
{
    // Splited integer and float values.
    float2 i = floor(st);
    float2 f = frac(st);

    float a = random(i + float2(0.0, 0.0));
    float b = random(i + float2(1.0, 0.0));
    float c = random(i + float2(0.0, 1.0));
    float d = random(i + float2(1.0, 1.0));

    // -2.0f^3 + 3.0f^2
    float2 u = f * f * (3.0 - 2.0 * f);

    return lerp(a, b, u.x) + (c - a) * u.y * (1.0 - u.x) + (d - b) * u.x * u.y;
}

冒頭で行っているのは fbm 関数を使ってノイズを得ることです。UV をもとに少しずつずらした位置からノイズを3つ、生成しています。ざっくり言えば3つの異なるノイズを取得していると考えてください。

実際に可視化すると以下のように違いがあることが分かります。

ノイズの違い

こうして得られたノイズを、それぞれ掛け合わせてさらに smoothstep で範囲を調整しています。

これも視覚化してみると以下のような形状をしていることが分かります。よりパキッとした境界になっていますね。これが smoothstep の効果です。

tの違い

そしてこの t1 〜 t3 の値を使って色をブレンドしていくと以下のような模様になっていきます。

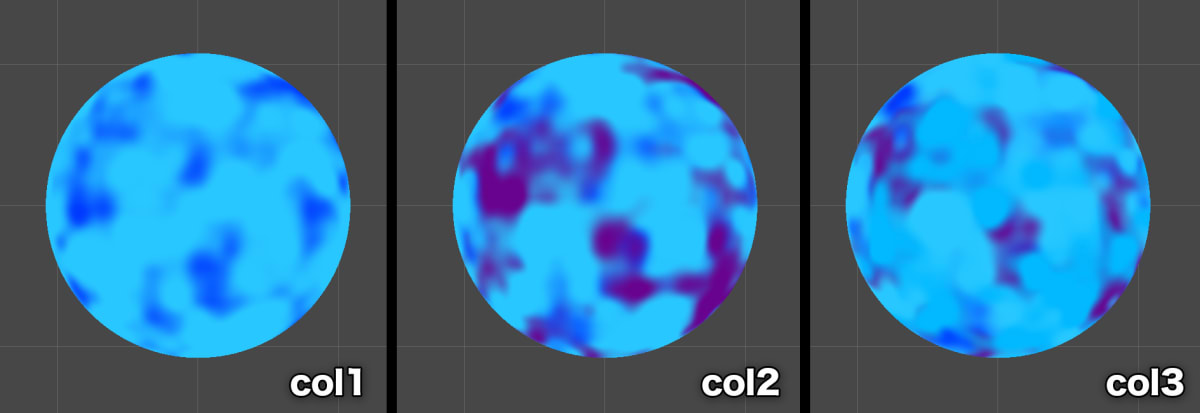
colの変化

このノイズは時間によって移動しているため、実際には流体のような動きを演出することができます。

動きの変化

ポイントとして、よく見ると d2 の計算だけ時間を減算しています。これによりひとつだけ反対方向に移動する効果が得られ、それを合成することで流体のようなゆらぎを演出しています。

最終工程ではリムライトやフレネル反射の計算を入れて冒頭のように、視線方向に応じて中央が透明になるようにしています。

詳細については以下の記事などを参考にしてください。

波エフェクト

次に見ていくのは波の表現部分です。

まずは距離を計算する部分を見てみましょう。計算の概要は以下の図のようになります。

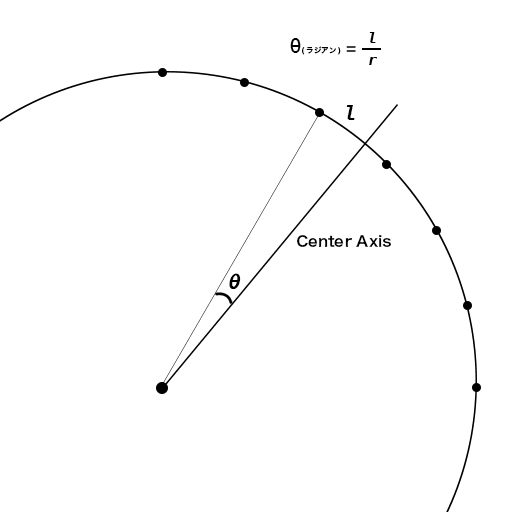
Center Axis

図を見てもらうと分かる通り、軸となるベクトルと成す角度（ $\theta$ ）から円弧の距離を求めることができます。具体的には図のラジアンの式に対して左右に半径 $r$ を掛けることで円弧の長さ $l$ を求めることができますね。

それを行っているのが以下のコードです。

中心軸からの距離を求める

// _CenterVectorはC#側から触れた点をもとに計算して渡される
float3 center = normalize(_CenterVector.xyz);

// 距離計算のために位置ベクトルを正規化しておく
float3 position = normalize(v);

// 内積を使ってコサインの値を求める
float cosTheta = dot(position, center);

// コサインの値から角度（ラジアン）を求める
float radian = acos(cos_value);

// ラジアンに半径を掛けることで円弧の長さを求める
float distance = radian * _Radius;

// 円周で割ることで正規化する
float normalizedDistance = distance / (2.0 * PI * _Radius);

上記のコードにより、軸から各頂点の距離を求めることができました。あとはこの距離をそのまま sin 関数に渡してやることで波を値（高さ）を取得することができます。

sin 関数で値を求めているのは以下の部分です。

波の高さを計算

// 前段で求めた距離に対して補正係数を掛け、さらに時間を引くことで波の動きを作る
float rad = distance * _WaveRatio - _Time.w;

// 軸から離れるほど波の高さを抑制する補正値を計算する
float influence = 1.0 - smoothstep(0, 0.3, normalizedDistance);

// 求めたラジアンを引数に波の高さを求める
float s = sin(rad) * _WaveSize * influence;

上記の高さ計算を適用すると頂点が波打つように移動します。

Wave

しかし、よく見るとなんとなく違和感があるかと思います。実は頂点シェーダで頂点を移動してしまっているので法線はそのままなのです。なのでライティングなどの陰影が正常に描画されていません。

法線の計算

最後は法線計算を見ていきます。法線計算のコンセプトは以下です。

頂点変形前の頂点の接線および従法線方向に少しだけ移動した2点を求める
(1)で求めた2点も、元の頂点と同様に変形を適用する
(2)で変形された2つの点の外積を求め、それを法線とする

簡単に言えば、変形前に少しだけずれた位置の点を用意し、変形後の空間で外積を使って法線を求める、ということです。

なぜこれで法線が求まるかと言うと、そもそも接線と従法線は法線に対して垂直です。そしてそのふたつのベクトルが成す平面に対して垂直ということは、その平面の法線に他なりません。

レイマーチングの実装をしたことがある人であれば、レイの位置を微細に変化させ、偏微分を求めてそれを法線とする方法に近しい考え方でしょう。

以下は上記計算のイメージ図です。変換対象の点とは別に、接線方向（青の軸）と従法線方向（赤の軸）に取った点が作るベクトルの外積を計算し、法線（緑の軸）を求めている様子です。

法線計算

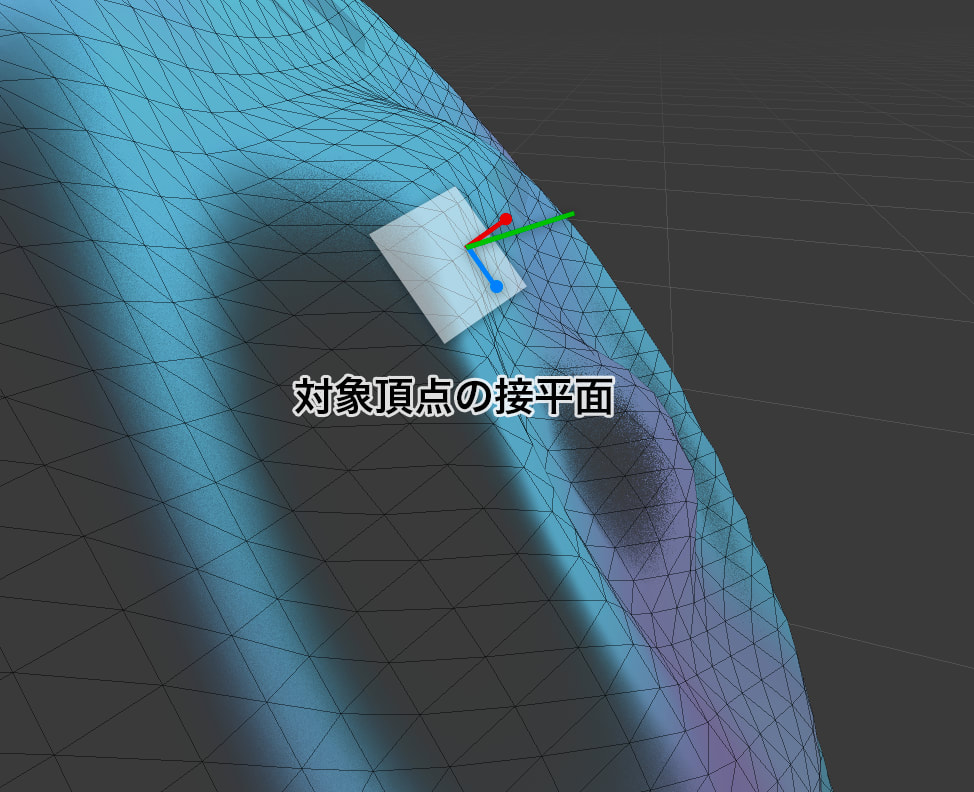
それを踏まえてコードを見てみましょう。それぞれなにをしているかはコメントとして記載しています。

法線の計算

// 接線と「元の」法線から従法線を求める
float3 binormal = normalize(cross(i.normal, i.tangent.xyz));

// 中心軸ベクトルを正規化
float3 center = normalize(_CenterVector.xyz);;

// 微小に移動するための値
float eps = 0.00001;

// 元の頂点に波の変形を適用する
float3 vertex = applyWave(i.localPos.xyz, center);

// 同様に、接線方向に少しだけ移動した点も変形する
float3 tangentVert = applyWave(i.localPos.xyz + i.tangent * eps, center);

// 従法線方向も同様
float3 binormalVert = applyWave(i.localPos.xyz + binormal * eps, center);

// 求めた点から頂点を引くことで、頂点のローカル空間でのベクトルに変換する
float3 localTangentVert = normalize(tangentVert - vertex);
float3 localBinormalVert = normalize(binormalVert - vertex);

// 接線方向に移動したベクトルと従法線方向に移動したベクトルの外積を求め、
float3 localNormal = cross(localTangentVert, localBinormalVert);

// 上記を法線とする
float3 normal = localNormal;

上記で求めた法線を適用すると、以下のようにライティングなどが適切にされるようになります。
ひとつ前のものと比べるとだいぶ質感が変わっているのが分かるかと思います。

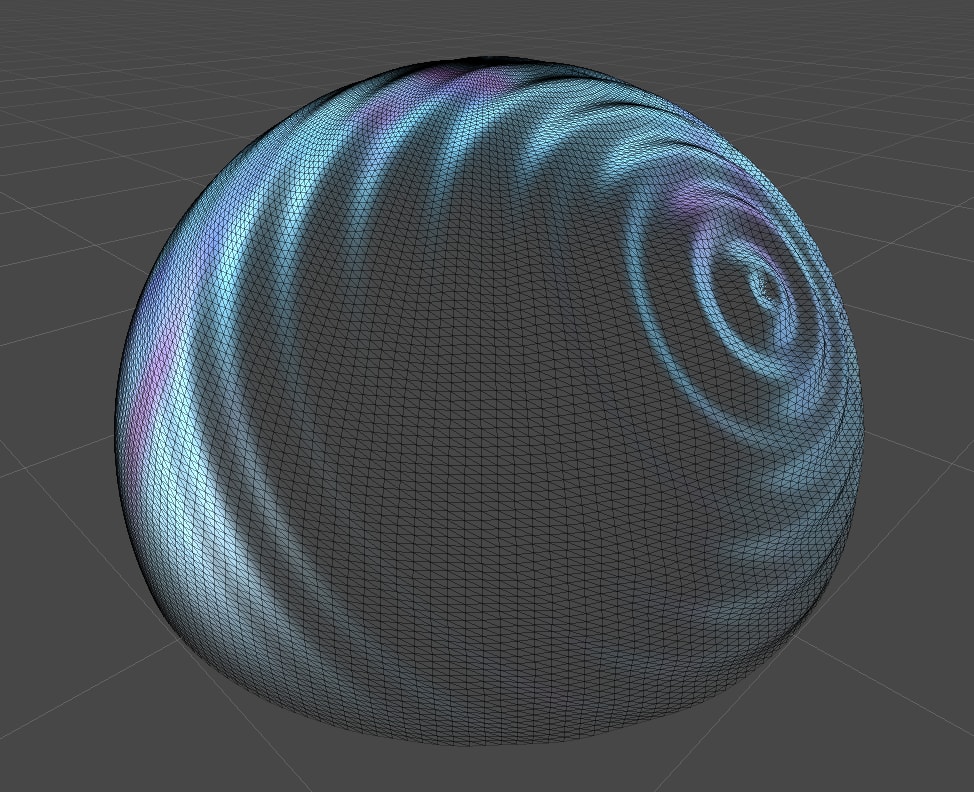
Wave with normal

最後に

実は法線を求める方法、最初はもっと別の形で考えていました。しかしどれもうまくいかず、どうしたらいいかをChatGPTに質問したら今回の実装方法を提案された、という背景があります。

最近は画像もそのまま認識するようになり、画像内の文字も問題なく認識するため「こういうことをやりたい」とかなりダイレクトに伝えて聞くこともできるようになってきました。GPTの出力するコードをそのまま使うのは推奨しませんが、方針としての実装例やコード例はどんどん聞いて引き出していきたいところです。

エンジニア絶賛募集中！

MESONではUnityエンジニアを絶賛募集中です！ XRのプロジェクトに関わってみたい！開発したい！という方はぜひご応募ください！

MESONのメンバーページからご応募いただくか、TwitterのDMなどでご連絡ください。

書いた人

比留間和也（あだな：えど）

カヤック時代にWEBエンジニアとしてリーダーを務め、その後VRに出会いコロプラに転職。コロプラでは仮想現実チームにてXRコンテンツ開発に携わる。 DAYDREAM向けゲーム「NYORO THE SNAKE & SEVEN ISLANDS」をリリース。その後、ARに惹かれてMESONに入社。 MESONではARエンジニアとして活躍中。
またプライベートでもAR/VRの開発をしており、インディー部門でTGSに出展など公私関わらずAR/VRコンテンツ制作に精を出す。プライベートな時間でも開発しているように、新しいことを学ぶことが趣味で、最近は英語を学んでいる。

GitHub / Twitter

MESON Works

MESONの制作実績一覧もあります。ご興味ある方はぜひ見てみてください。

MESON Cases

はじめに

コンセプトと実装方針

コンセプト

実装方針

実装解説

色のブレンド

波エフェクト

法線の計算

最後に

エンジニア絶賛募集中！

書いた人

MESON Works

Discussion