⚙️

Optunaによる多目的最適化を実験に組み込む

2023/10/26に公開

Python

はじめに

例えば製造業では、顧客要求物性を達成するための条件チューニング、あるいはプラント製造条件をチューニングする機会が数多くあるかと思います。
その際に、往々にして物性Aの値が良化すると物性Bの値が悪化するケースが存在するかと思います。
その際に使える機械学習の手法として、Optunaによる多目的最適化があります。
本記事ではOptunaによる多目的最適化を実験に組み込むためのサンプルコードを紹介します。

実装

サンプルデータの作成

サンプルデータの分布確認

まずは、今回使用するサンプルデータを作成します。
物性値の硬度と靭性を以下のように定式化します。
実際はこのように顕わな関数として定義できることはないので、あくまでサンプルデータとして考えてください。

硬度（ $\text{hardness}$ ）:

\text{hardness} = 0.5 \times \text{temperature} + 0.2 \times \text{pressure} + 0.1 \times \sqrt{\text{time}} + 5 \times \mathbb{1}(\text{material\_type} = 'A') + 2 \times \mathbb{1}(\text{material\_type} = 'B') + \epsilon_1

靭性（ $\text{toughness}$ ）:

\text{toughness} = \text{pressure} - 0.1 \times \text{temperature}^{1.1} + 30 \times \mathbb{1}(\text{material\_type} = 'A') + 25 \times \mathbb{1}(\text{material\_type} = 'B') + 20 \times \mathbb{1}(\text{material\_type} = 'C') + \epsilon_2

ここで、 $\mathbb{1}(\cdot)$ は指示関数で、その条件が真であれば1、偽であれば0を返します。また、 $\epsilon_1$ , $\epsilon_2$ は平均0、標準偏差2と1の正規分布に従うノイズです。

コードは以下の通りです。

# ライブラリ
import numpy as np
import pandas as pd
import japanize_matplotlib
import matplotlib.pyplot as plt

# サンプルデータの作成
def create_objectives(temperature, pressure, time, material_type, n_samples):
    hardness = 0.5 * temperature + 0.2 * pressure + 0.1 * np.sqrt(time)
    hardness += (material_type == 'A') * 5 + (material_type == 'B') * 2
    hardness += np.random.normal(0, 2, n_samples)

    toughness = pressure - 0.1 * temperature**1.1 + (material_type == 'A')*30 +(material_type == 'B')*25 +(material_type == 'C')*20
    toughness += np.random.normal(0, 1, n_samples)  # ノイズを追加
    
    return hardness, toughness

続いて、上記create_objectives関数をもとに、サンプルデータの分布を確認するためにデータを1000件（膨大な実験が行われた想定）作成します。

# データの数
n_samples = 1000

# 製造条件: 温度、圧力、時間、材料の種類
temperature = np.random.uniform(20, 100, n_samples)  # 20-100度
pressure = np.random.uniform(1, 10, n_samples)  # 1-10 atm
time = np.random.uniform(0, 60, n_samples)  # 0-60分
material_type = np.random.choice(['A', 'B', 'C'], n_samples)  # 材料A, B, C

# DataFrameにまとめる
hardness, toughness = create_objectives(temperature, pressure, time, material_type, n_samples)
df = pd.DataFrame({
    '温度': temperature,
    '圧力': pressure,
    '時間': time,
    '素材': material_type,
    '硬度': hardness,
    '靭性': toughness
})

得られたデータを見てみましょう。

display(df.head())

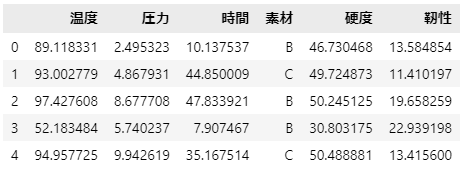
今回作成したデータは温度、圧力、時間、素材を特徴量として、硬度と靭性が目的変数となっています。

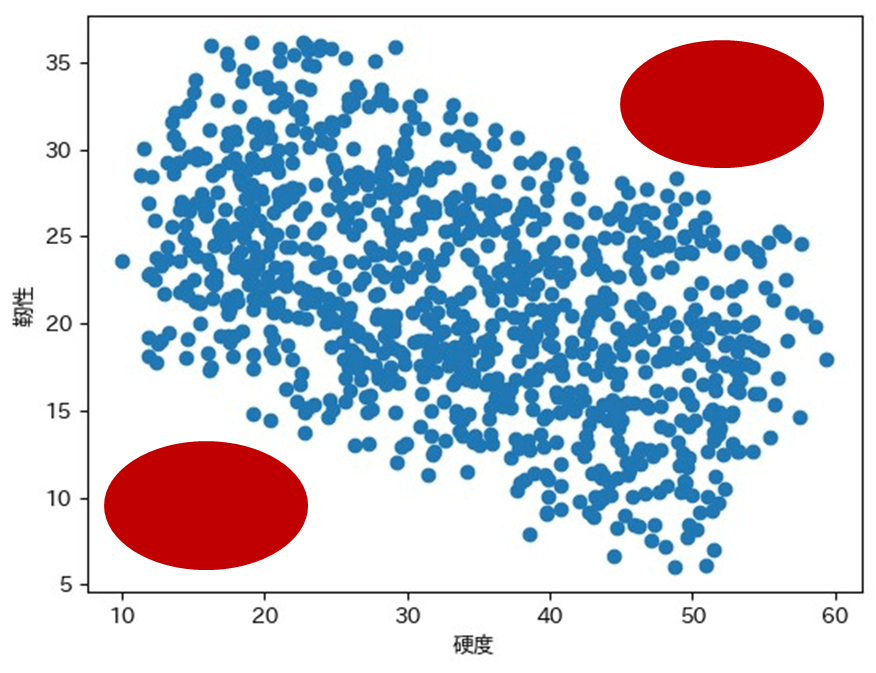
また、硬度と靭性の関係もプロットしてみましょう。

plt.scatter(df['硬度'], df['靭性'])
plt.xlabel('硬度')
plt.ylabel('靭性')
plt.show()

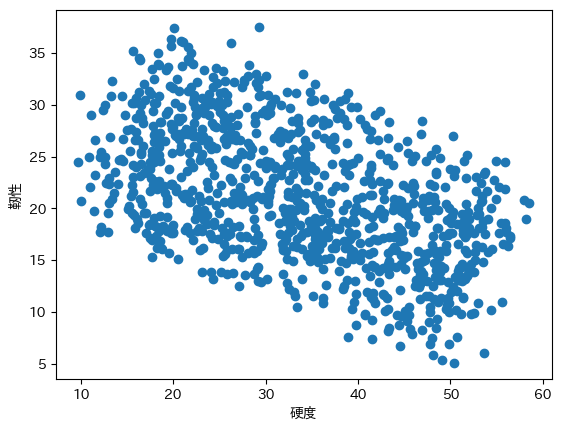
硬度が上がるほど、靭性は下がる傾向にあります。
これは、硬度に関しては温度が上がるほど上がるように設定したのに対して、靭性は温度が上がるほど下がるようにサンプルデータを作成したからです。
これは、実際の現場でもよくあることかと思います。

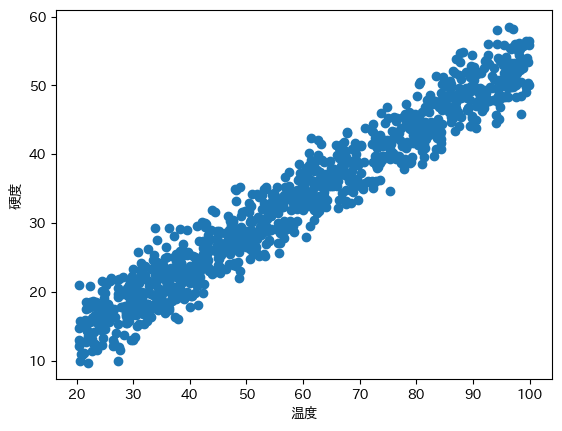
plt.scatter(df['温度'], df['硬度'])
plt.xlabel('温度')
plt.ylabel('硬度')
plt.show()

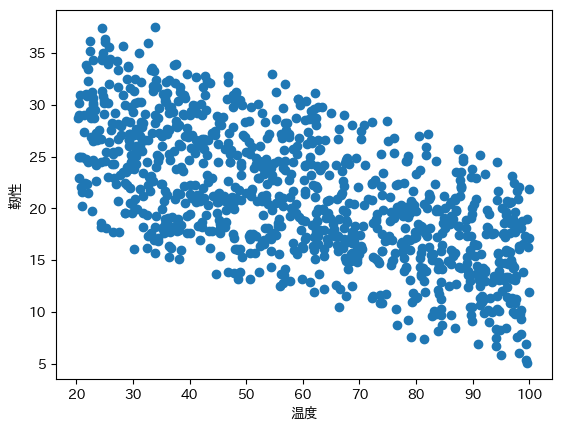
plt.scatter(df['温度'], df['靭性'])
plt.xlabel('温度')
plt.ylabel('靭性')
plt.show()

また、その他の関係も可視化しておきましょう。

import seaborn as sns
sns.pairplot(df, hue='素材', y_vars=['硬度', '靭性'], x_vars=['温度', '圧力', '時間'])
plt.show()

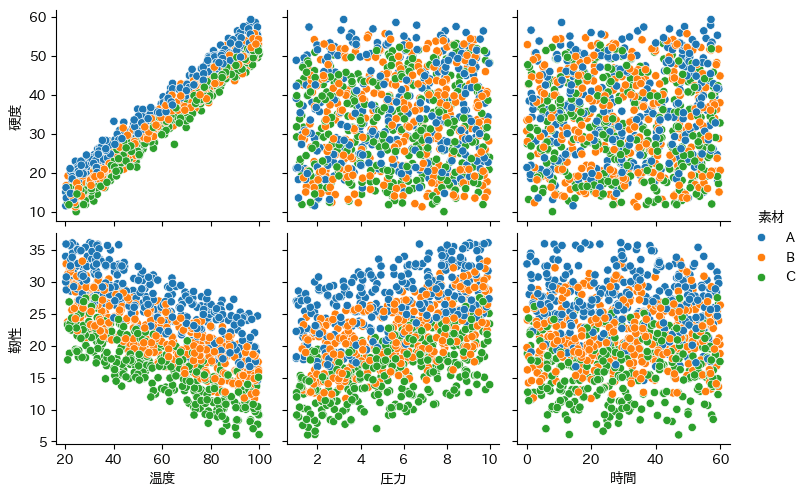
以上でサンプルデータの分布確認は終わります。

既に20件の実験が行われたと想定しデータを作成

先ほどはサンプルデータが1000件、つまり膨大な実験が既に行われている想定でデータを確認しました。これだけ実験が行われていれば、目標物性に向けてチューニングすることは容易、あるいは既存条件では不可能であることが見極められるでしょう。
一方で、実際には1000件もデータは無いことが多いでしょう。
そこで、例えば今回のケースでは20件の実験が行われたと想定してデータを作成します。

# データの数
n_samples = 20

# 製造条件: 温度、圧力、時間、材料の種類
temperature = np.random.uniform(20, 100, n_samples)  # 20-100度
pressure = np.random.uniform(1, 10, n_samples)  # 1-10 atm
time = np.random.uniform(0, 60, n_samples)  # 0-60分
material_type = np.random.choice(['A', 'B', 'C'], n_samples)  # 材料A, B, C

# DataFrameにまとめる
hardness, toughness = create_objectives(temperature, pressure, time, material_type, n_samples)
df = pd.DataFrame({
    '温度': temperature,
    '圧力': pressure,
    '時間': time,
    '素材': material_type,
    '硬度': hardness,
    '靭性': toughness
})

plt.scatter(df['硬度'], df['靭性'])
plt.xlabel('硬度')
plt.ylabel('靭性')
plt.show()

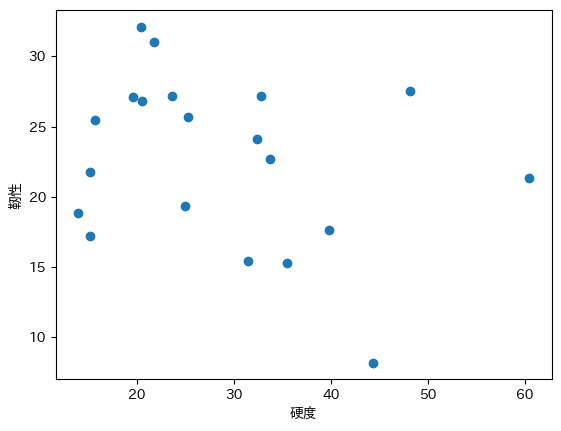
この結果を見ると、硬度と靭性にトレードオフの関係がありそうには見えます。

また、その他関係性も可視化してみましょう。

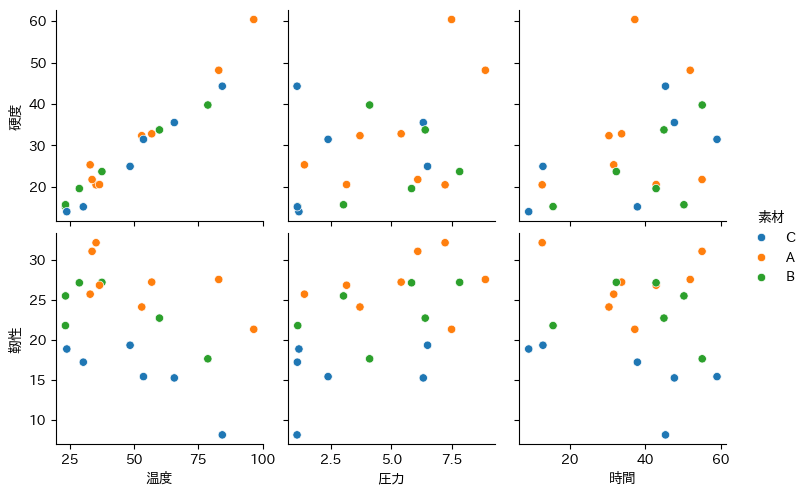
これらのデータが与えられた際に、例えば硬度50以上、靭性25以上という条件をクリアするための条件を見定めるのは難しいでしょう。
その際に使える機械学習の手法として、Optunaによる多目的最適化があります。

Optunaによる多目的最適化

Optunaとは

OptunaはPythonで使用できるブラックボックス最適化ライブラリです。
Optunaを使用すると、ある目的変数を最大化あるいは最小化するための特徴量を出力することができます。

Optunaを使用した多目的最適化の実装

実装フロー概要

以下、実装フローの概要になります。
既存データをOptunaのstudyに取り込んだ後、最適な実験をレコメンドしてもらい、目標物性に到達するまで実験を行います。

実装

まずは、特徴量探索範囲を指定し、実施した20個の結果をoptunaのstudyに追加します。
尚、今回目標とする硬度と靭性はそれぞれ50以上、25以上とします。
その他、細かい事項はコード内コメントに記載しています。

import optuna
import pandas as pd

# 目標とする硬度と靭性
target_hardness = 50
target_toughness = 25

# Optunaのstudyオブジェクトを作成
# サンプラーはOptuna独自のベイズ最適化を利用したTPESamplerを使用。理由は速いから。
# multivariate=Trueにすることで全ての特徴量の関係を考慮できる。
# n_startup_trialsを0にした理由として、今回は既にランダムにデータを20個持っているからランダムにn回レコメンドする必要がない。ただ、デフォルトは10なので今回のケースでは0にしなくても結果は変わらない。
sampler = optuna.samplers.TPESampler(multivariate=True, n_startup_trials=0)
study = optuna.create_study(directions=['maximize', 'maximize'], sampler = sampler)

# 探索範囲を指定
search_space = {
    '温度': optuna.distributions.FloatDistribution(20, 100),
    '圧力': optuna.distributions.FloatDistribution(1, 10),
    '時間': optuna.distributions.FloatDistribution(0, 60),
    '素材':optuna.distributions.CategoricalDistribution(['A', 'B', 'C'])
}

# 実施した試験結果を追加
for i, row in df.iterrows():

    params = {
        '温度':row['温度'],
        '圧力':row['圧力'],
        '時間':row['時間'],
        '素材':row['素材'],
        }   
	
    study.add_trial(optuna.trial.create_trial(
        params=params,
        distributions=search_space,
	
	# 目的変数はそれぞれ、目標値までの差分とする
        values=[row['硬度']-target_hardness, row['靭性']-target_toughness]
    ))

続いて、ループ部分の実装になります。
ここで、実際は実験を行う毎に記録をしていくことになると思いますが、今回はサンプルのため、ループを回して最適化を行っていきます。
尚、先ほど可視化したグラフより、温度が高いほど硬度は上がる傾向があったので、レコメンドする温度範囲は75～100としています。
また、実験のレコメンドと実験結果の追加はOptunaのAsk-and-Tellインターフェースを使用しています。study.add_trialでは初期に作成したsearch_spaceとレコメンド範囲が異なると、解が得られないケースが出ました。

for i in range(100):

    # Optunaで次の実験をレコメンド
    trial = study.ask()
    
    # 次の実験範囲を指定し、レコメンドした値をner_paramsに格納
    new_params = {}
    new_params['温度'] = trial.suggest_float('温度',75, 100) # 75～100とする
    new_params['圧力'] = trial.suggest_float('圧力',1, 10)
    new_params['時間'] = trial.suggest_float('時間',0, 60)
    new_params['素材'] = trial.suggest_categorical('素材',['A', 'B', 'C'])
    
    temperature = new_params['温度']
    pressure = new_params['圧力']
    time = new_params['時間']
    material_type = new_params['素材']
    n_samples = 1
    
    # 実験を行ったという設定で硬度、靭性を取得    
    new_hardness,new_toughness = create_objectives(temperature, pressure, time, material_type, n_samples)
    new_hardness,new_toughness = new_hardness[0],new_toughness[0]
    print(new_hardness,new_toughness)
    
    # studyに実験結果を記録
    study.tell(trial, [new_hardness-target_hardness, new_toughness-target_toughness])
        
    # 目標値を上回れば終了
    if new_hardness >= target_hardness and new_toughness>=target_toughness:
        break

上記コードを実行し、得られた結果を見てみましょう

display(study.trials_dataframe())

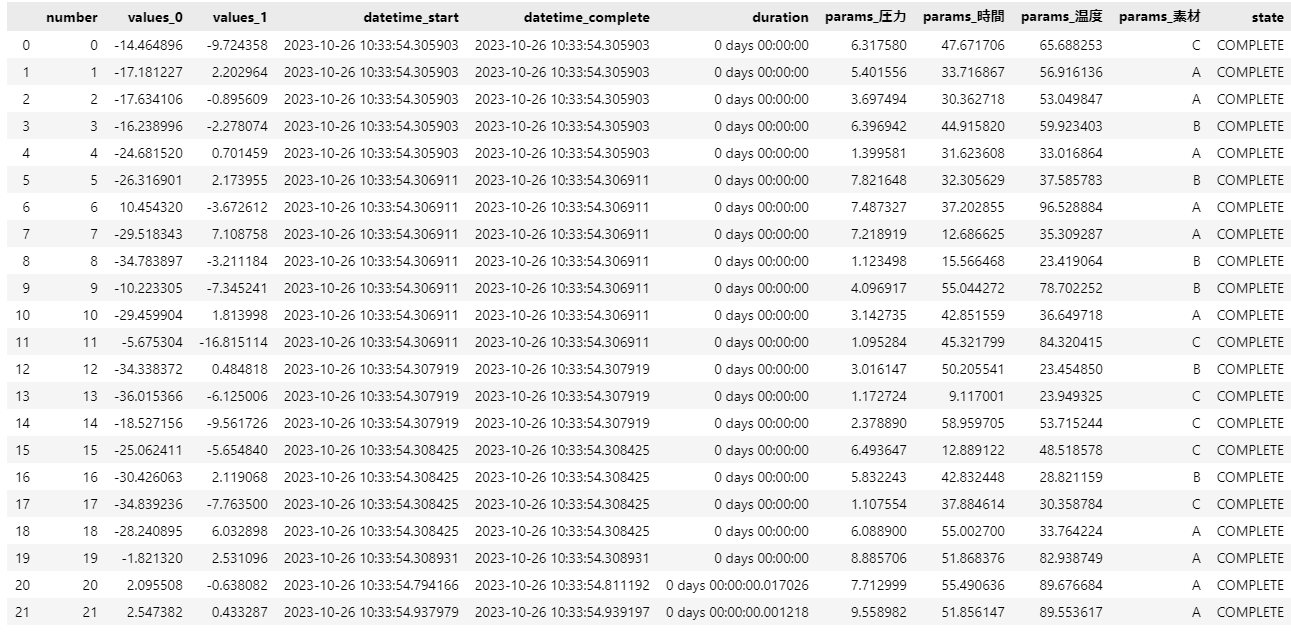
最初の20回は初期実験結果のため、2回の実行で目標物性にたどり着けたことがわかります。
これは中々良いのではないでしょうか。
尚、レコメンドする温度範囲を20～100とすると目標物性にたどり着くまでに35回の実験が必要となりました。
このように、既存実験結果の傾向やドメイン知識により、探索範囲を絞ることが、最適解にたどり着くまでのスピードに大きな影響を与えることがわかります。

おわりに

以上でOptunaによる多目的最適化を実験に組み込むためのサンプルコードの紹介を終わります。
Optunaの理論は難しいところもあるのですが、実装は簡単にできることがわかったかと思います。
また、ドメイン知識や基礎分析により得られた傾向を適切に探索範囲に反映させることの重要性もわかりました。
また、実務で適用する際は、あくまでco-pilotとしてドメイン知識との整合性を確認しつつ水準を選択するといった使い方もあると思います。
一方で、赤丸で囲った部分は現在の特徴量では賄えない物性であり、人間の創造性が試される部分になるかと思います。