🕌

GNN（Graph Neural Network）のガイダンス

2024/03/11に公開

Python

gnn

グラフニューラルネットワーク

tech

この記事について

GNN（Graph Neural Network）の概要について調査を行い、サンプルコードを作成しました。

まずはGNNの概要を説明し、その後GNNの学習イメージやサンプルコードを紹介します。

より詳細なGNNに関する情報は↓レビューが参考になります。

GNNとは？

GNNはデータがグラフ形式で表現される場合に適用することができる深層学習のフレームワークです。グラフ $G$ はノード（点） $V$ とエッジ（線） $E$ で構成され、数式的には $G = (V, E)$ で表されます。
また、グラフの構造は例えば隣接行列 $A$ で表現できます。 $A$ が以下の場合、ノード①-ノード②とノード②-ノード③にはつながりがあるが、ノード①-ノード③にはつながりがないことを表現できます。

A = \begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \end{pmatrix}

また、ここの数値を0、1の2値ではなく連続値とすると、ノード間のつながりに加えて重みも表現することができます。例えば、路線図をイメージすると駅間の距離・つながりをノード間の重みとして表現することができます。また、各ノードの特徴量を $V$ と表現することができます。路線図の例では、特徴量として駅周辺の人口、地価、住所等が候補になり得ます。

GNNの問題タイプと応用シーン

GNNの問題タイプは下記のように大きく3つのカテゴリに分類されます。

ノード単位の分類・回帰:

グラフ内の個々のノード（例えば、論文、人物、商品など）について、特定の属性やクラスを予測します。たとえば、論文の被引用関係をグラフとして表現し、GNNを用いて個々の論文が属する研究分野を分類することができます。

グラフ単位の分類・回帰

グラフ全体に対する属性やラベルを予測します。例えば、分子の構造をグラフで表現し、そのグラフ全体のポテンシャルエネルギーを予測する場合があります。

リンク予測

グラフ内の任意の二つのノード間にエッジ（つまり、関係やリンク）が存在するかどうか、またそのエッジの性質（例えば、強さや重要度）を予測します。このアプローチは、例えばあるユーザー（ユーザーノード）がある商品（商品ノード）を購買するか否かをグラフとして表現し、学習することでユーザー・商品毎の購買確率を予測することができます。

このように、GNNを使うことで解くことができる課題は多岐に渡ります。一方で、これらの課題は既存手法でも解くことが可能です。次章ではGNNが既存の手法に比べて持つメリットについて解説します。

既存手法に対するGNNのメリット

GNNのメリット

GNNのメリットは、テーブルデータでのモデリングにおいて、グラフ構造に関する複雑な特徴量エンジニアリングを行わずとも、既存の手法と同等、あるいはそれを超える精度で分析が可能になる点にあります。例えば、分子のポテンシャルエネルギーを予測するタスクがあるとします。ポテンシャルエネルギーは分子の化学構造に起因するため、分子の化学構造を表形式の特徴量として表現する必要があります。特にどの原子とどの原子が繋がっているのか、という点は特徴量として組み込みたい点ではありますが、それをテーブル形式の特徴量として表現するのは手間がかかります。一方で、分子構造をグラフとして表現することで、そのグラフをGNNのアーキテクチャに当てはめれば、特徴量エンジニアリングをすることなく、GNN側で自動で特徴量抽出を行うことが可能です。

参考となるkaggleコンペ

実際にGNNが適用され効果を発揮した例として、以下kaggleコンペを紹介します。

コンペタイトル

OTTO – Multi-Objective Recommender System

コンペ概要

e-commerceのセッション情報をもとに、クリックされる、カートに入れられる、購入される可能性が高い商品を予測（レコメンド）するコンペとなっております。

GNNの適用について

7位の解法にGNNがアンサンブルモデルの一つとして用いられていました（Discussionは存在するが、具体的なコードは不明）。
解法の概要としては、以下フローで32個の特徴量を持つGNNの学習を進めたようです。

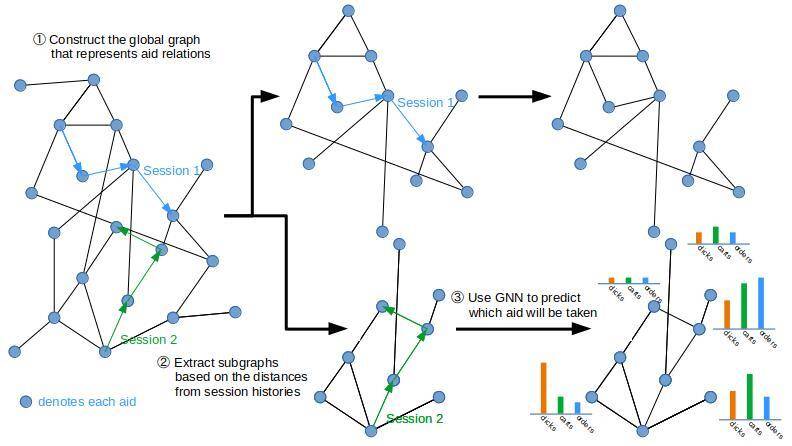
①. トレーニングデータの一部を用い、ユーザーの商品→商品移動を集計し、遷移確率が高い商品を集計し、商品-商品間の遷移確率を表すグラフを作成。
②. 対象セッションで選択された商品に対する近傍商品を取り出す。
③. 各近傍商品に対して、クリックされる、カートに入れられる、購入されるかを予測。

学習の結果、もう一つのアンサンブルモデルであるLightGBMモデルと遜色ない精度（Recall@20）のモデルがGNNで作成されたとのことです。注目すべきは、LightGBMモデルが344個の特徴量を用いているのに対し、GNNモデルはその約1/10にあたる特徴量数でこれを実現している点です。この事例から、GNNを使うことで、より少ない特徴量で高い精度のモデルを構築できる可能性があることがわかります。特に、商品間の遷移確率など、複雑な関係性を直接的にモデル化することができるため、特徴量エンジニアリングの手間を大幅に削減しながら良好なパフォーマンスを得ることが可能となります。

weight	Public LB	Private LB
LightGBM Part	0.60025	0.60008
GNN part	0.59894	0.59874
Final Submission 1	0.60311	0.60307
Final Submission 2	0.60302	0.60313

GNNの学習イメージ（CNNとの比較）

ここからはGNNの学習イメージについて、CNNと比較することで、直感的に理解できるように説明します。

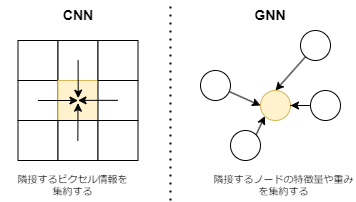
CNN（畳み込みニューラルネットワーク）

CNNは、画像などのグリッド構造データを扱う際に用いられる深層学習の一種です。このモデルは、あるピクセルの情報（特徴）を、その周囲のピクセルの情報と組み合わせることで抽出します。具体的には、対象ピクセルに対して、隣接するピクセル群から特徴を集約します。このプロセスにより、局所的なパターンやテクスチャを捉えることができます。

GNN（グラフニューラルネットワーク）

一方、GNNは、あるノードの特徴を抽出するために、そのノードに隣接するノードから情報を集めます。この情報には、隣接ノードの特徴量や、ノード同士を繋ぐエッジの重み（エッジがどれだけの情報を持っているか）が含まれます。GNNでは、これら周辺ノードからの情報の集約に関して様々な方法が存在します。

GNNの代表的な手法

GNNではCNN等の画像タスクと同様に、対象となるノードに対して周辺ノードの情報をどのように情報を集約していくか、がポイントとなります。情報の集約方法として色々な例が模索されている中で、以下が代表的な手法になります。

手法	概要	特徴	参考論文	データセットの内容
GCN	対象ノードの近傍ノード全ての特徴量を演算してノード表現を畳み込み計算。最もシンプルな畳み込み層。	近傍ノード全ての表現を取り入れることができるが、グラフ情報を全てメモリに載せる必要があり、大規模グラフにおける計算コストが高い。	https://arxiv.org/abs/1609.02907	PubMedデータセット: 糖尿病に関する科学論文。ノード数：19717、エッジ数：44338、特徴量数：500、クラス数：3
GraphSAGE	対象ノードの近傍ノードの一部をサンプリングし、近傍ノードの特徴量を集約してノード表現を計算。	サンプリングを行うことでGCNに比べて計算コストが低く、近傍ノードの情報を集約して学習を行うため未知ノードに対しても適用可能（inductive）。	https://arxiv.org/abs/1706.02216	Reddit data: Redditの投稿。ノード数：232,965、特徴量数：300、クラス数：50
GAT	近傍ノードを含む特徴量を重み付けを行った上で取り込む。inductiveな予測も可能。	関連性が高いノード間での情報伝達を強化する。	https://arxiv.org/abs/1710.10903 https://arxiv.org/abs/2105.14491	PPI: タンパク質間の相互作用のグラフ。ノード数：56944、エッジ数：818716、特徴量数：50、クラス数：121

GCN（Grapgh Convolutional Network）では全ての隣接ノードの情報を対象ノードに集約していきます。情報集約の計算で最も重要な部分は $AX$ で表されます。ここで $A:隣接行列、X:特徴行列（各ノードの特徴量）$ となります。この式を計算すると、対象ノードに隣接している特徴量を足し合わせたものが行列として得られます。以下、具体的な数値を入れて計算を行った例です。

% 隣接行列 A A = \begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \end{pmatrix}, % 元の特徴ベクトル X X = \begin{pmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{pmatrix}, AX = \begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{pmatrix} = \begin{pmatrix} 2 & 5 \\ 4 & 10 \\ 2 & 5 \end{pmatrix}

この計算を繰り返すことで対象ノードから離れたノードの情報も対象ノードに集約されていきます。一方で、これはグラフ情報を全てメモリに載せる必要があり、グラフの規模が大きくなると計算コストが高く、メモリが不足する可能性があります。また、学習時にグラフ全体の隣接行列を必要とするため、新規のノードに対する予測（例えば、新規の論文が追加された場合の論文分類予測）ができません。この課題を解決するために、GraphSAGE（Graph Sample And Aggregate）が発案されました。この手法では対象ノードの近傍ノードの一部をサンプリング）した上で、近傍ノードの特徴量を集約することで計算コストの増加を回避しています。また、この手法は新規のノードに対しても、近傍ノードの情報を集約する計算を適用することができるため、新規ノードにも対応可能です。更に、LLMでも使用されているようなAttention機構をGNNにも適用したのがGAT（Graph Attention Networks）になります。こちらの手法では、隣接ノードの情報集約を行う際に、全ての情報を均等に集約するのではなく、対象ノードと隣接ノードの類似性をもとに隣接ノード毎に重みを付けて情報を集約する手法になります。GCNは基本的に計算負荷が高いため、現実的にはGraphSAGE、あるいはその発展形のGATを使用するのが好ましいと考えられます。尚、CNN等の画像分類タスクと異なる点として、ResNetやViT等のデファクトスタンダード的なアーキテクチャが存在せず、例えば集約の計算を何回行うか等のハイパーパラメータチューニングはタスクに応じて調整する必要があります。次章ではGNNのハイパーパラメータチューニングについて紹介します。

GNNのハイパーパラメータチューニング

以下論文でチューニングされているパラメータを確認したところ、基本的に、CNNと同様のハイパーパラメータがチューニング対象となり、GNN固有のパラメータは無いようです。

https://arxiv.org/pdf/2104.06046.pdf

チューニング対象となるハイパーパラメータを下記に挙げます。

チューニング項目	概要
畳み込み層の数	ネットワークの層の深さ
畳み込み後の次元数	各層のembedding後の次元数
Poolingの方法	Max, Mean等
活性化関数	Lelu等
Dropout	層間の出力の一部を学習時にランダムに0とする
Skip Connection	層を飛ばして、ネットワークの情報を伝達する

GNNが使えるPythonライブラリ

Pytorch系ではPyTorch GeometricとDeep Graph Libraryが主に使用されており、PyTorch Geometricの方がGitHub上では人気です。

GNNの各問題タイプの実装例(Pytorch Geometric)

以下にGoogle Colaboratoryによる実装例を紹介しています。
Pytorch Geometricを使用することで、基本的にPytorchの書き方でGNNのモデルを実装し学習・予測を行うことができます。

グラフ中のノードのクラスを予測

グラフのクラスを予測

グラフ中のノード間にリンクが存在するか予測

GNNの計算量確認

ノード予測に関して、重いデータであってもミニバッチ学習により、計算ができることを確認しました。

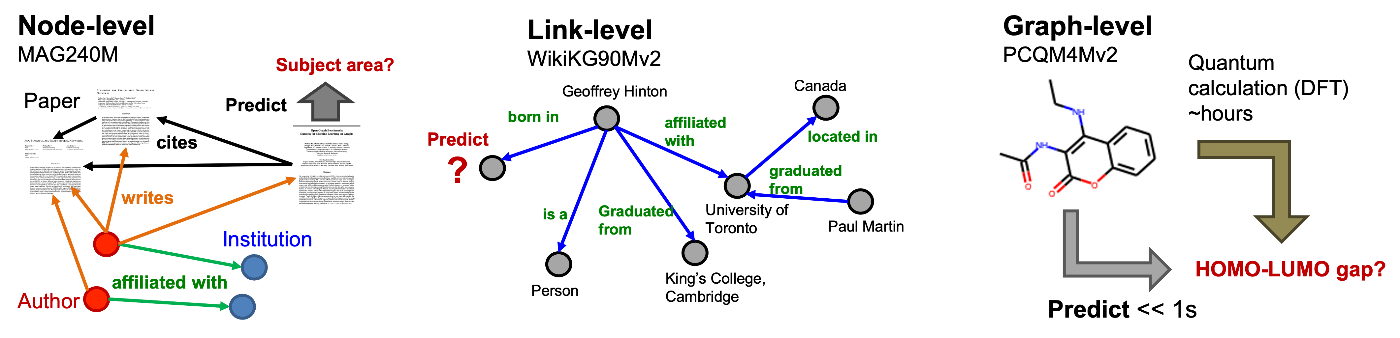
参考：ベンチマークとなる大規模なデータセットと応用例

Open Graph Benchmarkにベンチマークとなるグラフデータがまとめられています。
以下、大規模なベンチマークデータの抜粋になります。

データセット	タスク	データの概要	ノード数合計	グラフ数	エッジ数合計	ダウンロードサイズ
MAG240M	ノード予測	多種多様な学術分野の論文が含まれる学術グラフで、論文が属する学問分野の予測を目的としています。	244,160,499	1	1,728,364,232	167GB
WikiKG90Mv2	リンク予測	知識をグラフ化したデータセットで、グラフ内の欠けている関係（リンク）を見つけ出すことが目的です。	91,230,610	1	601,062,811	89GB
PCQM4Mv2	グラフ予測	分子の量子化学的性質を扱うデータセットで、特に分子のエネルギーレベル差（HOMO-LUMOギャップ）を予測することを目指しています。	52,970,652	3,746,619	54,546,813	59MB