AHC045参加記【暫定362位】
問題
ざっくりとした最終解法
- 各点において、とりあえず正方形の中心を真の座標として扱う
- 各グループの大きい順に、
- 各点のx + yの昇順のうち、どこグループにも所属していない点を選択する
- その点からの距離が短い順に点を選択していき、グループを構築する
- そのグループのなかでMSTを構築する
- 各グループにおいて、以下を行う
- Lよりサイズの大きいグループについては
- 適当なグループ内の点を一つ選び、それを根とする木構造を構築する
- 根から遠い方から、クエリを使って暫定のMSTに修正をかけていく
- L以下のサイズのグループについては
- グループ全体をクエリにかけてその結果をMSTとして採用
- 提出
https://atcoder.jp/contests/ahc045/submissions/64605257
暫定362位 31.56G
ビジュアライザ
Seed = 2, Score = 229512

解説1 初期解改善部分まで
この下の画像はseed = 2のやつを基本的に使用する
とりあえずはサンプルにならって、正方形の中心を座標として扱う。のちのちクエリで修正するかもなーと思いつつ、そういうのができるようにclassとかを定義していった。
とりあえず初回の提出は点をindex順にGiごとに区切っただけ、辺もindex順につなげただけの適当なやつ。
見れたもんではない。

その後、MSTを構築するメソッドを手元に用意した上で、グループ分けをxの昇順に行う形に変更。
縦線が多いのは当然ではある。

ここからは、山登りや焼きなましでグループ間の点を入れ替える方針をいろいろ試していた。
ただ、スコアはほとんど改善しないか、悪化するまであったのでこの方針は一旦捨てた。
そういえば山登りや焼きなましは良い解から初期解が遠すぎるとそもそもたどり着けないみたいなことがあるというのを思い出し、初期解の改善に取り組むことに。
様々な形を試した結果、2の方法にたどり着く。
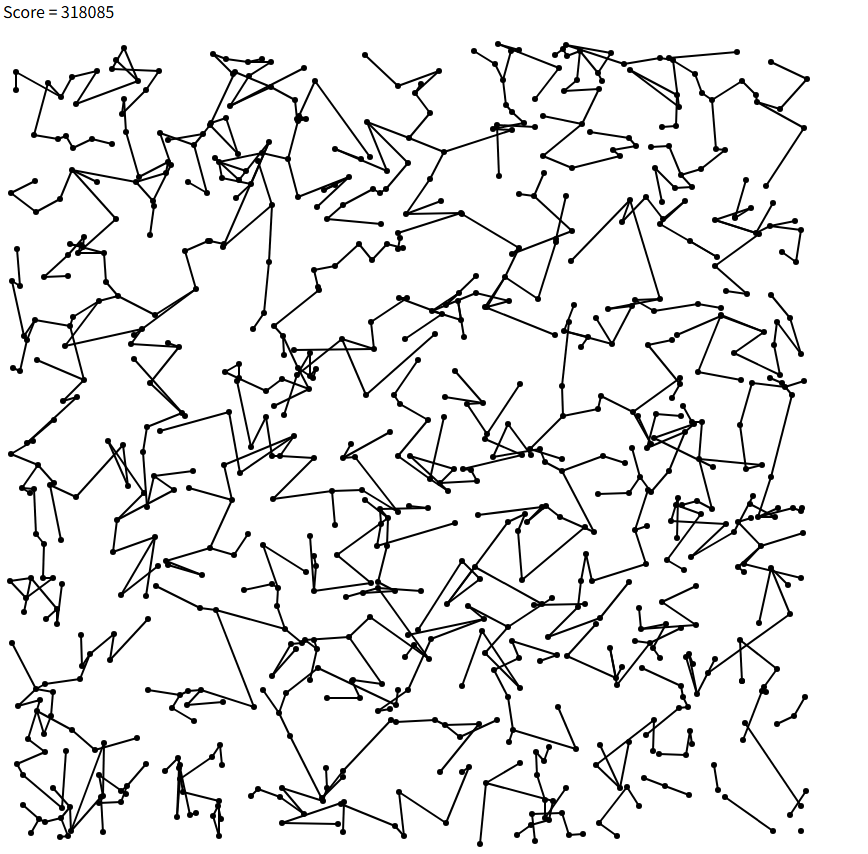
この初期解改善が全体の中ではかなり大きな改善になった気がしている。
解説2 クエリをつかった改善
そもそも、グループのサイズがクエリの大きさ最大L以下の場合、グループ全体をクエリにかけてその結果を採用すればええやんということに気づき実装。右下のグループ数が少ないあたりではごちゃつきが少しだけ改善された。

問題はこのあとで、グループのサイズがLより大きい場合のクエリを使った修正方法が思いつきそうで思いつかない段階が続く。
その後、グラフをL以下の部分木に切る -> クエリにかける -> 残りの部分に同様の処理を繰り返していく、というのを思いついた。その時には、L以下で最大の部分木がとれるように、木構造からdfsで下のノードの数を数える、というのをやってみた。
例えば、こういうグラフがあったとする。(こういうグラフを生成できて整った見た目にできるやつ教えてくれ~)

この場合、ノード8には[8]、ノード10には[8, 5, 0, 13, 10, 3]みたいな情報を載せておく。
例えばL = 6の場合、ノード10を選べば最大部分木になるのでノード10とそれにぶら下がっているノードでクエリをかける。L = 5の場合はノード13が選ばれる形。
その後、クエリの結果をそのまま保存しておく。そして、今回クエリにかけられたノードをこの木から消す。但し、L = 6でノード10が選ばれた場合、ノード10は残しておく。残りの[8, 5, 0, 13, 3]の情報を消す。 でないと、クエリの結果をそのまま出力に使用できない(グラフが切れるため)。
また、コーナーケースとしてL = 3で以下のようなグラフが残ってしまう場合がある。

根を変えればなんとかなりそうではあるが、今回は一旦こんな感じになった場合、クエリによる修正を打ち切って、この5ノード全体で手元でMSTを構築してクエリ結果に足す。また、途中でクエリ結果を使い切った場合も同様に残りの部分で手元で構築したMSTをクエリ結果と統合する。
これを行うことで、ここまで改善された。これが大体最終提出になっている。
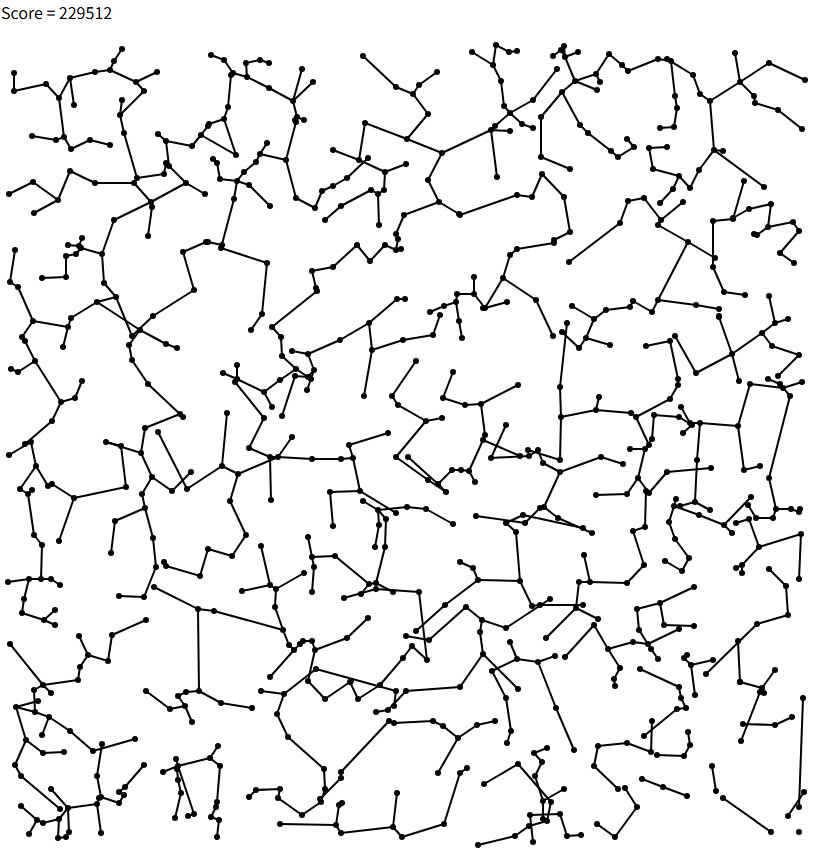
まとめ
すこしずつ改善して提出するたびにスコアが上昇するというAHCの楽しさが存分に味わえたコンテストではあった。
ただ、
- そもそも取り掛かり始めたのが金曜日(嫁の出産は全てに優先するため当然ではあるが・・・)
- Lが小さい場合はこの方法だとろくに改善されないはずなのでなんか別の方法を思いつきたかった
- そもそも点の誤差範囲の情報は全く使っていない
と、改善点は結構ある。次も頑張りたいですね。
Discussion