牛はボールかドーナッツか、それとも…~トポロジーで考えてみる柔らかい世界~
はじめに
球形の牛という単純な科学モデルで考えてしまった故ののジョークがあります。
牛乳の生産量が低かったとある酪農家が地元の大学に手紙を書いて学術的な支援を求めた。様々な分野の教授たちが協力を約束し、理論物理学者がリーダーになることが決まった。
農場で2週間かけて徹底的な調査が行われた後、教授たちは大学へ戻り、データがつまったノートをリーダーに預けた。後は報告書にまとめるだけだった。するとすぐに物理学者は農場へと逆戻りして、酪農家にいった。「解決策が見つかりました。まず球形の牛を真空状態においてください」
wikipediaより引用
このように、科学の世界では、複雑な事象を考えるときに、そのままではあまりにも複雑なため、単純に考えるきらいがあります。計算が難しいから、球形として…立方体として…etc…。
ここで、気になるのは当然のように牛を球状のものとして捉えることは正しいのでしょうか、球体そのものとしてみなしてよろしいのでしょうか。ほんの少しだけ真面目に考えてみます。
※ 若干の数学的な概念は出すものの、この記事自体は、暇つぶし程度に読んでいいただけば幸いです。
そもそも「同じ」ってなんだろう
しばしば、りんごが2個、えんぴつが2本と、我々は数という概念を使い特定のグループに所属しているものを同一視することがあります。ここで、考えたいのは2個のりんごは本当に同じりんごと見なして良いかどうかです。完全に区別できる「長野県産りんご」と「青森県産りんご」、「HBの鉛筆」と「2Bの鉛筆」等の存在があったとして、我々は果たしてそれらを一緒にし2個や2本と考えて良いのでしょうか。
数学的における同じ~一般化~
すべてが違ってしまうと同じとして扱うのにかなり狭い範囲でのやりとりになってしまい、やや物事を語るのに不都合となります。この問題を解決するために一般化という数学の知識を借りましょう。
一般化とは共通の持っている性質や特徴に注目し、それを抽象化することです。
三角形同士を同じとみなそう
一般化の例として三角形の合同条件や相似条件での例を見てみましょう。

画像は証明をするための条件を詳しく書いていないですが少なくとも条件を定めれば
などいったことが導けることでしょう。ここでも合同や相似というある種の「同じ」という概念がでてきたのがお分かりでしょうか。
さらに、そこに続き
共通の性質に着目すれば同じ括りにできる
一般化と呼ばれるものを使うことによって、今回は別の三角形ではあるが形や大きさに関しての共通の持っている性質や特徴に注目してあげることで、ある種の同じ三角形だということができました。先程、例に出した鉛筆やりんごも数え方は等しいみたいな共通する性質に着目してあげれば、1,2,3...と言うように、ちゃんと数えることができそうですよね!
このように一般化をしてあげれば区別付けられるものでも同じものとして考えることができます。
牛は球体?
改めて、牛と球体は同一視できるか?ついては、上記の考えを使ってあげれば
- 牛の持つ性質や特徴
- 球体の持つ性質や特徴
に注目してあげることで答える事は出ることでしょう。
一般化をする考える上では、どのような視点でやってあげるかが重要です。例えば、息をしている、模様があるか、角があるみたいな部分を見ても球体には全部ないのでやっぱり違うじゃん・・・となるでしょう。三角形の時は「形」や「大きさ」に注目して、共通なものを抽出して考えておりました。
今回はあえて真っ先に除外されそうである「形の性質」に着目して、この問題に挑んでみます。え、ぶっとんでますって?はい、そうですとも、エンジンがかかってきました!もっともっと色々な見方をしていきましょう!
やわらかいゴムみたいな世界で考えるトポロジー
今回は、位相幾何学、別名「トポロジー」という数学界では柔らかい幾何学と呼ばれている分野で考えていきます。トポロジーは「何らかの形を伸ばしたり曲げたりしても保たれる性質(ただし、切ったり貼ったりはしない)」という「位相不変量」に注目し、その性質をもとに形を分類していきます。
少し文章だとわかりにくいですね。以下のGifをご覧ください。このアニメーションは、立方体を三角錐へ、さらに球体へと連続的に変化させたものになります。
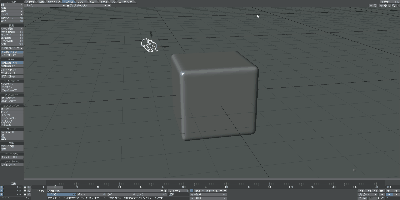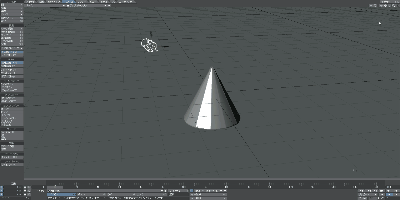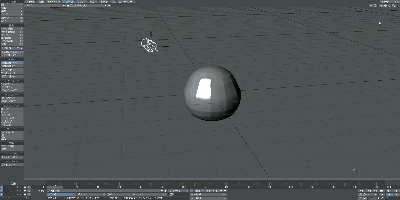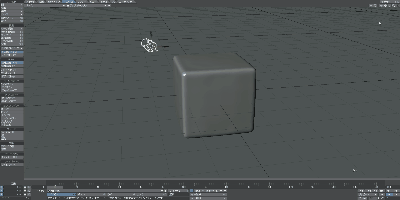
このように立方体を伸ばしたり曲げたりして三角錐やら球体とやらを作り出すことができました。すなわち、立方体や三角錐や球体はトポロジー上は 同じ形(同相と言う) とみなすことができます。
要点としては、切り貼りなしに連続的に変化させていくことでその形状にできるかどうかです。
穴の数で考えてみるコーヒーカップとドーナツ
この分野を利用するのであれば、マグカップとドーナッツは同相という事実にたどり着けます。
少し歪ですが、これもアニメーションで確認してみましょう。
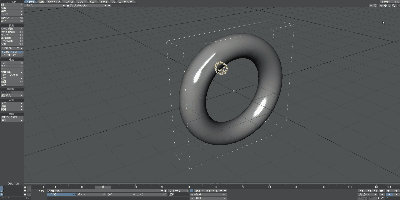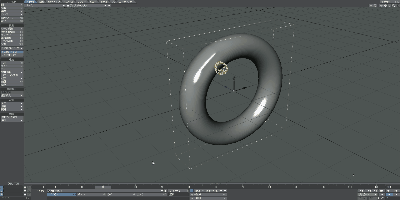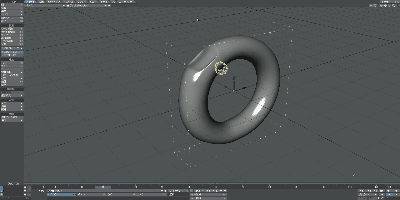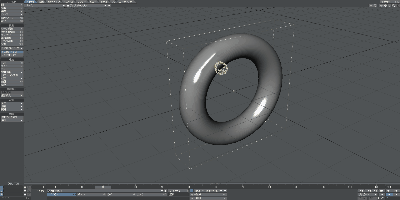
ご覧の通り、頑張ばって変形すればドーナッツからマグカップにできることが分かりました。すなわち、これらはトポロジー上では等しいということが言えます。
トポロジーの分類の仕方の1つとして、空いている穴の数に注目するというものがあります。理由として、穴の数は伸ばしたり曲げたりしても変わらないためです。
先程の例だと、ドーナツとコーヒーカップはそれぞれ1つずつ穴がありますね。また、立方体や球体は穴がありません(つまり0個の穴)。視点を変えてみれば、どんなに頑張って変形しても、球体からドーナッツ、もしくはその逆の変形は不可能です。すなわち、これらは異なる形ということになります。
このようにトポロジーでは、ある形の特定の性質に注目してもっと広い視点で形を分類することができます。このあたりをもっと詳しく説明したいところですが、今回は感覚的な理解で十分だと思われるのでここまでにします(そもそも「穴」とは?みたいな話やそのためのホモロジー群の説明が必要になってしまい、記事が長くなりすぎてしまうため…)。
牛は球体ではなさそう
さて、ようやく本題に入ることができました。
冒頭に書いた「牛を球状のものとして捉えることは正しいのか?」についてですが、牛の体の形状から球体と変形できるのでしょうか。結論からすると同相ではないと言えます。
下記の図をご覧ください。

図の通り、牛には少なくとも食道の存在があります。他にも鼻腔やら何やらありますが、そこを口と一体化して単純化しても、なお大きな空洞があります。これは上記の例で考えると球体よりもドーナツのほうが分類する上ではより適当であるということになります。すなわち、牛をトポロジー的に注目した場合には、球体として扱うのは、無理があるということでしょう。
まとめ
牛のジョークからそもそも「同じ」というものが、数学上どういったものかを考察し、ある性質に注目してするということが大切ということが分かりました。今回はトポロジーという分野での不変的な性質の1つである穴の数に注目することで、牛は球体ではなかったということが分かりました。
今回はトポロジーという側面から形に注目して考察しましたが、他の分野から考えると、また違った結論が導き出せるかもしれませんね。
以上です。ここまで読んでいただきありがとうございました。


Discussion